【初心者向け】群数列とは？奇数の群数列を例題にやさしく解説｜第n群の総和・何群・何番目

そもそも群数列とは何か？について、本記事では初心者向けに解説していきます。群数列のつまづきポイントとして、第n群の総和の求め方や、ある項が「何群目・何番目」に当たるか判断する方法が分からず苦手意識を持つ人は多いです。

本記事では、奇数の数列を例に群数列の典型問題の考え方を、図や表を用いて基礎から丁寧に解説していきます。群数列の見方・一般的な解き方・計算の流れが一度で理解できる内容になっています。高校数学の数列が不安な方でもスッキリ整理できるので、ぜひ読み進めてみてください。

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

群数列とは？
群数列で必要な予備知識
群数列の基本問題
本記事のまとめ

群数列とは？

数列をいくつかの塊ごとに区切った数列のことを、「群数列」といいます。例えば、以下の数列を見てください。

$$1, 4, 9, 16, 25, 36, 49, 64, 81, 100, \cdots$$

これは、一般項$\small a_n = n^2$の数列ですが、これを、3つおきに区切って、

$$1, 4, 9 | 16, 25, 36 | 49, 64, 81 | 100, \cdots$$

とすると、3つずつの塊がいくつもできますね。この塊を「群」といい、群を持った数列なので、群数列と呼ばれています。

群数列とは

・数列を塊に区切ったもの。
・区切り方に規則性がある。

同じ数列でも、区切り方によって異なる群数列になります。例えば、さっきの数列を、

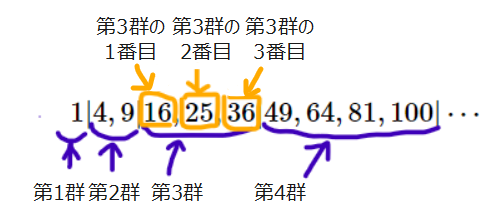
$$1|4, 9 | 16, 25, 36 | 49, 64, 81,100| \cdots$$

と区切ることもできますね。この時、初めの塊を「第1群」、2つ目の塊を、「第2群」といいます。
そして、群の中で、先頭の項から順に、1番目、2番目、…と数えていきます。「25」であれば、
3つ目の塊の最初から2番目にあるので、第3群の2番目ですし、第4群の3番目であれば、「81」になります。

最初のうちは簡単なのですが、「第100項目の50番目の数字って何？」みたいに、数が多くなると
書き出すこともできないので、ある程度数学的に考えていく必要があります。そこで必要な知識を
次の章で紹介します。

群数列で必要な予備知識

群数列では、第n群の総和やある項が「何群の何番目」に位置するかを求める問題がよく出ますが、実はこれらの計算をする際に用いるのは、等差数列や等差数列の和の公式になっています。

というわけで、改めて等差数列と等差数列の和の公式についておさらいしておきましょう。既に理解している人は飛ばしてしまってOKです。

2.1 等差数列の一般項

等差数列とは、数列が一定の間隔で増えたり減ったりする数列のことでした。

【等差数列の例】
・$\small 1,3,5,7,9,11,\cdots$　⇒2ずつ増える数列（奇数列）
・$\small 5,10,15,20,25,30,\cdots$　⇒5ずつ増える数列
・$\small 7,4,1,-2,-5,-8,\cdots$　⇒3ずつ減る数列

このように増減が「一定の数」になっていることから「等差」という名前がついています。

等差数列の一般項

等差数列の第$\small n$項目は、初項を$\small a$、公差を$\small d$とすると
$$a_n=a+(n-1)d$$

2.2 等差数列の和

等差数列の和を考えます。数列、$\small 1,3,5,7,9,11,\cdots$で、初項から、第6項の和を求めたければ、次のように考えれば、求められます。

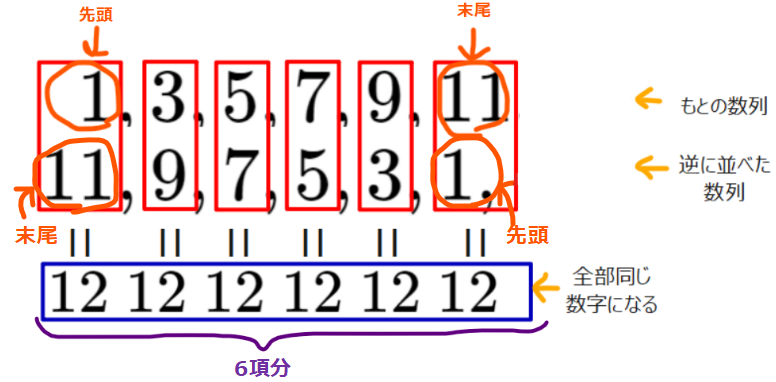
まず、上の図のように、初項から第6項を抜き出した数列と、それらを逆に並べた数列を上下に並べます。次に、それらを縦に足していくと、等差数列の場合は、すべて同じ数になります。同じ数が、6項分できてきれいな感じになりましたが、実は、上の図の青枠の合計は、もとの数列の和の2倍になっているのがポイントです。なぜならば、青枠の数字は、もとの数列と、それを逆に並べた数列の合計で、数列を逆にしても、和は同じだからです。よって、青枠の合計を2で割ると、もともと求めたかった数列の和になります。

ここまで、言葉で説明したことを数式で計算すると、次の3ステップ。

・STEP1：$\small 1+11 = 12$
⇒ 先頭と末尾を足す（厳密には、先頭と末尾じゃなくてもいいけどこれが一番わかりやすい）
・STEP2：$\small 12×6=72$
⇒ 同じ合計が項数分あるので、項数で掛け算
・STEP3：$\small 72÷2=36$
⇒ 求めたい数列の和は、半分なので2で割る

これを、公式的にまとめるとこんな感じです。

等差数列の和の公式

$\small n$項分の和を求めるとき、求める和を$\small S_n$とすると、
$$S_n=\frac{\{(先頭)+(末尾)\}×n}{2}$$

参考：等差数列の和の図形的意味

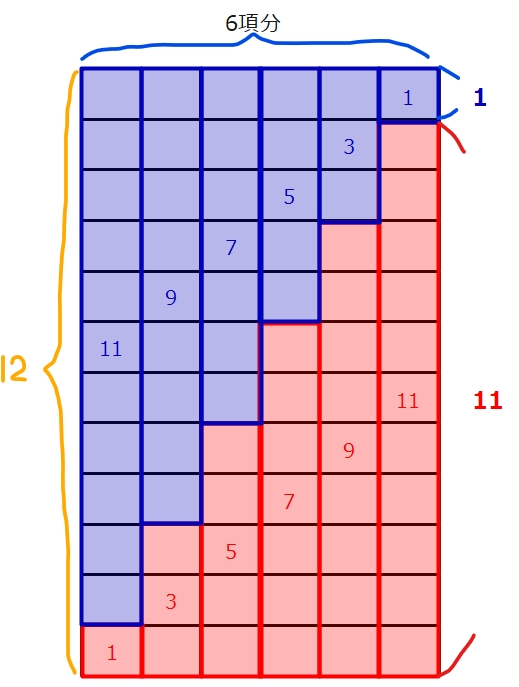
合計がすべて同じになるのは、等差数列が、一定の間隔で増減しているからで、よく下図のような階段に例えられます。もとの数列を赤とすると、数列の和を求めるというのは、赤色のブロックの個数を求めるということなので、一旦、逆さにした青色の数列を考えて、ブロックの段差をつなぎ合わせ、きれいにデコとボコをはめることで、ブロックの数は、縦12、横6のブロックの個数の半分になるので、簡単に求めることができるのです。

2.3 個数と序数

最後に、群数列の問題で「何群目の何番目か」を求めるときに必要となる知識として「個数」と「序数」の違いについておさらいしておきましょう。

群数列では、「個数」と「序数」を混同しないように気を付ける必要があります。

・個数とは　…数列の場合は群の中に何個の項があるかを表すときに使う。
・序数とは　…物の順番を表す言葉で、数列の場合は「第何項目」など先頭からの項の位置を表すときに使う。

ここで一つ問題です。3秒以内に答えてみてください。

下図はとある群数列の一部を表しています。群の初項が第10項目で末項が第15項目だとすると、この群には全部で何個の項があるでしょうか？

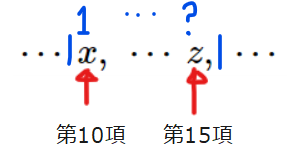
$\small 15-10=5$個！…と答えたくなりますが、正解は6個ですね（冷静に考えると分かってしまうので冒頭に3秒以内で答えてと書いてました）。

なぜ感覚とずれるかというと、第10項目や第15項目というのは数列の先頭からの位置、砂和たち序数になっています。一方で、今聞かれているのは群の中に項が何個あるかという個数になっているので、序数と個数のズレを意識しないといけないからです。

個数と序数は1つずつずれます。群数列では、何個かや何番目かなど個数と序数の両方を使いながら計算する必要があるので、ミスしないようにすることが大事です。ミスしないためには、ちゃんと数えられればベストなのですが、あまりにも個数が多い場合は、全部数えるわけにもいかないので、「小さい数で個数と序数の関係性を確認する」という方法がおすすめです。今回の問題のように第10項～第15項の場合（小さい例）を例に、単純引き算すると$\small 15-10=5$だけど、実際の個数は6個だから、引き算した結果に1を足せば個数になる、という関係性を確認できます。この関係性は数が大きくなっても変わらないので、例えば、第145項目～203項目は何個かを求めたければ、$\small 203-145+1=59$個と求めることが可能です。これは、覚えておきましょう。

群数列の基本問題

問題

奇数の数列を、$\small 1\space | \space 3,\space 5 \space | \space 7,\space 9,\space 11 \space | \space 13,\space 15, \space 17,\space 19 \space | \space 21,\space \cdots$のように、第$\small n$群が$\small n$個の数を含むように分けるとき、
(1) 第$\small n$群の総和を求めよ。
(2) 301は第何群の何番目に並ぶ数か。

[昭和薬大　改題]

解答

(1)
今回考える数列は、奇数列なので、2ずつ増加する等差数列になります。なので、第$\small n $群の総和は、予備知識で解説した等差数列の和の公式を利用すればよいですね。そのためには、第$\small n $群の先頭と末尾を求めておく必要があります。

第n群の項数はn個なので、等差数列の公式にあてはめると、
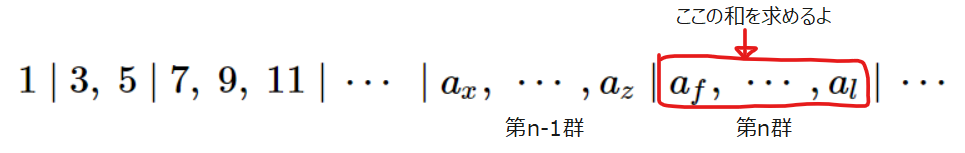
\begin{split} S_n &=\frac{\{(先頭)+(末尾)\}×n}{2}\space\space\\ &=\frac{(a_f+a_l)×n}{2}\\ \end{split} こんな感じになるので、あとは、先頭$\small a_f$と末尾$\small a_l$を求めればokですね。さらに、第$\small n $群の先頭を求めるためには、第$\small n $群の先頭が、奇数列の第何項目にあたるのかを求めれば、よさそうですね。ひとまず、第$\small n $群の先頭を第$\small f$項目、末尾を第$\small l$項目とおきます。$\small f$は、$\small n-1$群目までの項数合計の一つ次で、1群目の項数は1項、2群目の項数は2項、$\small \cdots$、$\small n-1$群目の項数は、$\small n-1$であることから、
\begin{split} f &=[1+2+3+ \cdots +(n-1)]+1 \\ &= \frac{\{1+(n-1)\}×(n-1)}{2}+1\\ &=\frac{n(n-1)}{2}+1\\ &=\frac{n^2-n+2}{2} \end{split}

末尾の項数$\small l$は、$\small n$群目の項数が$\small n$項であることから、$\small f$に$\small n-1$を足せばよいので（nを足すではないので注意。項数がn個あるということは、間は、n-1個になる）、 \begin{split} l&=f+(n-1)\\ &=\frac{n^2-n+2}{2}+(n-1)\\ &=\frac{n^2+n}{2} \end{split} 奇数列の第$\small m$項目は、$\small a_m=2m-1$とあらわせるので、第$\small f$項目と、$\small l$項目は、 \begin{split} a_f &=2f-1\\ &=2×\frac{n^2-n+2}{2}-1\\ &=n^2-n+1 \end{split} \begin{split} a_l &=2l-1\\ &=2×\frac{n^2+n}{2}-1\\ &=n^2+n-1 \end{split} よって、求める第$\small n$群の総和を$\small S_n$とすると、 \begin{split} S_n &=\frac{\{a_f+a_l\}×n}{2}\\ &=\frac{[(n^2-n+1)+(n^2+n-1)]×n}{2}\\ &=\frac{2n^3}{2}\\ &=n^3 \end{split} と求められる。検算として、n=3の場合、第3群の総和は、$\small 7+9+11=27=3^3$であり、一致している。
(解答)　第$\small n$群の総和は、$\small n^3$。

～躓きポイント解説～
Q:第$\small n $群の先頭が何項目か求めるときに、1群目からn群目までを足してから1加えるということは、 $$\sum_{k=1}^{n-1} (2k-1)+1$$ ではないのでしょうか。
A:何を求めているのかに注意しましょう。今回求めたいのは、第n群の先頭が、奇数列の何項目に当たるのかを求めるのが目的です。つまり、求めるものは、「項数」になります。上の式だと、第1項目から第n-1項目の「数列の合計」になってしまいます。普通の数列の問題だと、数列自体の和を求めることが多いのですが、群数列では、項数を求めることがあるので、ごっちゃにならないように注意しましょう。

(2)
第$\small m$群に含まれるとする。第何群に含まれるか知りたい場合は、目印として群の先頭の数をまずは把握しましょう。
第$\small m$群の先頭は、(1)の$\small a_f$の結果から、 $$a_f=m^2-m+1$$ これが301を超えないmが見つかれば、そこが301が属する群になります。あとは頑張って当てはまるmを探せばよいのですが、少し見つけにくいので、$\small m^2-m+1=m(m-1)+1$と式変形してあげると、大体$\small m(m-1)≒m^2$で探してあげればよさそうです。$\small 17^2=289,18^2=324$なので、例えば$\small m=17$で$\small m^2-m+1$に代入してあげると、273（第17群目の先頭）、$\small m=18$だと、307(第18群目の先頭)で、301を超えました。つまり、第17群目のどこかに301がいるとわかります。ここからは、求め方は、いろいろあるので、お任せですが、例えば、私だったら、307が近いので後ろから攻めます。301は奇数列では、307の3つ前です。第17群は17個の奇数が並んでいるので、その後ろから3番目ということは、前から数えると、15番目になります。なので、第17群、15番目と分かります。

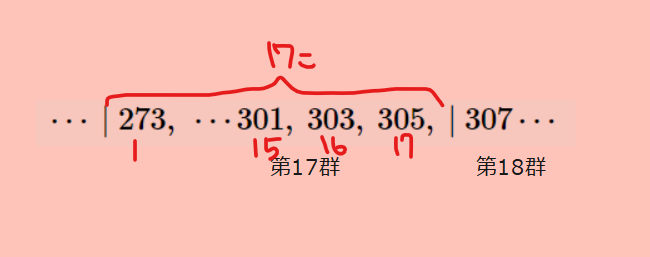
もう少し、数学的にかっちり解きたければ、第17群を、初項273、公差2の等差数列として、 \begin{split} & a_n =273+2(n-1)\\ \Leftrightarrow \space & 301 = 2n+271\\ \end{split} を解けばよく、 $$2n+271=301$$ $$2n=30$$ $$n=15$$ と求まります。
(解答)　第17群、15番目。