【数列】Σ（シグマ）記号の意味と公式の覚え方について分かりやすく解説｜計算のコツ・和の公式との違い

数列の学習で避けて通れないのが「Σ（シグマ）」記号。和を表すことは知っていても、実際にどのように計算するのか・和の公式とどう関係するのか分からないという人も多いのではないかと思います。

そこで本記事では、Σの意味・和の公式との違い・覚えておくべき公式・計算のコツについて分かりやすく解説します。初めて学ぶ人でも理解できるように、例題を交えながら1つずつ説明していきます。

　本記事はこんな人におすすめ

Σ（シグマ）記号について「足し算の記号らしいけど仕組みがわからない」と感じている人
等差数列や等比数列でも和の公式が出てきたけど、Σ（シグマ）とどう結びつくか知りたい人
シグマの公式の覚え方・考え方が知りたい人
「公式は暗記したけど使いどころがわからない」、「計算のコツが知りたい」と感じている人

　本記事のレベル

重要度

低

余力あれば

普通

必須

高
難易度

易しい

易

やや易

やや難

難

難しい
暗記/理解

暗記重視

暗記

半々

理解

理解重視

Σ（シグマ）記号の意味・公式を徹底解説
【例題付き】Σ（シグマ）の計算方法を徹底解説
1. 【演習問題】公式を用いたΣ計算のコツ
本記事のまとめ

Σ（シグマ）記号の意味・公式を徹底解説

【講義1】Σ（シグマ）とは？意味と書き方を超シンプルに解説

数列の勉強をしていると突如出てくる「Σ」ですが、Σはギリシャ文字で”シグマ”と読みます。数学ではちょいちょいギリシャ文字が登場してくることがあり、円周率の$\small \pi$や解と係数の関係で2次方程式の2解 $\small \alpha ,\beta$など。Σもこのようなギリシャ文字の一種です。

さて、数列に出てくるΣはどんな意味を持っているのか。それはずばり、「足し算」を表す記号です。シンプルですね。足し算の答えである和を英語でSummationというのでその頭文字「S」をギリシャ文字にして「Σ」という記号にしたわけです。

でもどんな足し算でもΣを使って表せるわけではなく、規則性のある数の足し算を表すときに使えるのがΣ記号になります。もちろん、規則性がある数＝数列というわけで、数列の分野で登場しているというわけです。

例えば、$\small 1+3+4$というのは特に規則性がないのでΣで和を表すことはできません。一方で、$\small 1+3+5$は「奇数」もしくは「初項1、公差2の等差数列」という規則性がある数列になっているので、Σ記号を用いて

$$\small \sum_{k=1}^3 (2k-1)$$

のように表すことができます。表し方については次章で詳しく解説します。

【補足】Σ記号の書き方
Σって普段書かない文字なのでどう書くのがいいのか迷いますよね。学校の先生の書き方を真似すればよいと思いますが、私は↓のように書いています。

ちなみにこれは余談ですが、私が海外に留学していた時に数列の授業を受けたんですが、その先生は、↓のような感じで上から下に向かって一筆書き（Wを横にしたみたいな感じ）で書いていてました（笑）。

面白い書き方だったので、たまに私もこの書き方をすることがあります（笑）。結構、人や国によっても書き方が違うのかもしれないですね。

【講義2】Σ記号の定義・使い方

Σが規則性のある数の足し算を表すことを理解できたところで、ここからは具体的に足し算をどのようにΣ記号で表すのか、あるいはΣ記号で表現された和をどのように足し算の形に書き下すのかについて解説していきます。

Point：Σ（シグマ）記号の定義

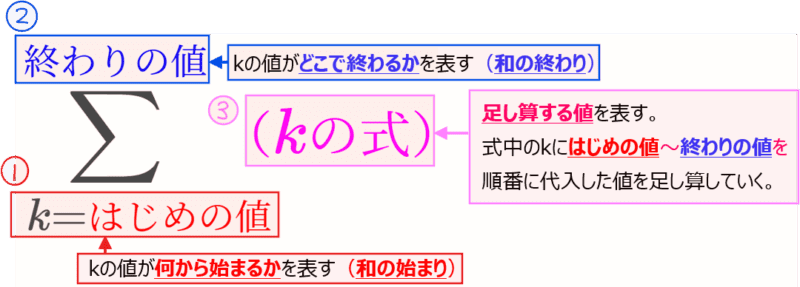
Σは規則性のある数の足し算を表す記号なので、規則性がある数というのは数列のように適当な変数を用いて表すことができます（例えば奇数の数列であれば$\small 2k-1$のように）。仮に変数を$\small k$とした場合、変数$\small k$を用いて表された式が③の$\small k$の式であり、規則性のある数のことを表しています。

変数$\small k$には数字が入る訳ですが、$\small k$がどの値からどの値までの和を取ればいいのか分からないと足し算の計算ができません。そこで$\small k$の値の範囲を表しているのが①、②の部分になります。①が$\small k$の値がなにで始まるか、②が$\small k$の値がなにで終わるかを表しています。

今説明したことを具体例で解説します。例えば、1～5までの数をそれぞれ2乗した数の和、

$$\small 1^2+2^2+3^2+4^2+5^2 \space \cdots (*)$$

をΣ記号を使って表したいとします。足し算している各項の値は変数$\small k$を用いて$\small k^2$（$\small k=1,2,3,4,5$）と表すことができるので、③の$\small k$の式に当てはまるのは$\small k^2$です。次に、変数$\small k$の値の範囲ですが、和の最初は$\small 1^2$なので、$\small k^2$と照らし合わせると$\small k=1$となっていることから、はじめの値は$\small k=1$（①の部分）と分かります。同様に、和の最後は$\small 5^2$なので、$\small k^2$と照らし合わせると$\small k=5$となっていることから、終わりの値は$\small k=5$（②の部分）です。

以上を踏まえて$\small (*)$をΣを使って表すと

$$\small \sum_{\color{red}{k=1}}^{\color{blue}5}\color{magenta}{k^2}$$

となります。

今後は逆にΣを使って

$$\small \sum_{\color{red}{k=2}}^{\color{blue}4}\color{magenta}{\frac{1}{k}}$$

と表された式を具体的な和の形に書き下していきましょう（和の計算まではしなくてOK）。

足し算している1つ1つの数は③部分の$\small k$の式を見ればよかったので、今回であれば、$\small \displaystyle \frac{1}{k}$になります。では、変数$\small k$にはどんな値が入るかというと、Σ記号の上下の①②部分を見てあげれば変数$\small k$の範囲が分かるのでした。今回であれば$\small k=2$から始まって、$\small k=4$で終わるということが分かるので、$\small k=2,3,4$が足し算の範囲になります。

以上より、具体的な和の形は

$$\small \sum_{k=2}^4 \frac{1}{k}=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$$

となります。

【講義3】Σ記号の使いどころは？

Σ記号の定義や使い方は分かったけど、結局Σ（シグマ）ってどんな時に使うの？と思った人も多いのではないでしょうか。

よくある勘違いとしてΣ（シグマ）を使えばどんな和でも計算できると思っている人がいますが、これは間違いです。Σ（シグマ）は、ただの和を表す記号です。なのでΣ（シグマ）で表した和が具体的に計算できるかどうかは別問題です [*1]。

*1：補足
$\small 2$を100回掛け算することを$\small 2^{100}$と表すことはできても実際に$\small 2^{100}$を計算できるかどうかが別問題というのと似ています。

例えば、講義2で出てきた分数の和をΣで表すと

$$\small \sum_{k=2}^4 \frac{1}{k}$$

となりますが、$\small \displaystyle \frac{1}{k}$の和の公式というものはありません。なので、例えば『1～100までの逆数の和をΣ記号で表せ』という問題があったら

$$\small \sum_{k=1}^{100} \frac{1}{k}$$

というように表すことはできますが、実際に計算して値を求めることはできません（頑張って計算するしかない…）。

計算できないならΣ記号を使って表せても意味ないじゃん？と思うかもしれないですが、必ずしもそうとは言えません。もしΣ記号がなかったら1～100までの逆数の和を数学的に表現するには

$$\small 1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{100}$$

のように途中を「…」で省略して記載するしかありません。でも、途中部分を省略してしまうと、この式だけを見た人は途中がどうなっているのかを最初の数項から想像するしかなく、人によって解釈がズレてしまう可能性が出てきます。

一方で、Σ記号を使って

$$\small \sum_{k=1}^{100} \frac{1}{k}$$

と表現しておけば、これは誰がどう見ても「1～100までの逆数の和」になります。しかもΣ記号を使った方が圧倒的にシンプルに表現できます。

このようにΣ記号は規則性がある数の和全般を表せるという点で非常に威力を発揮します。

Point：Σ（シグマ）記号の使いどころ

規則性はあるけど足し算の式を全部書ききれない場合に、正確に式を記述するときにΣ記号が役立ちます。

【講義4】和の公式とΣの違い

ここでは、等差数列や等比数列でも和の公式が出てきたけどΣ（シグマ）と何が違うの？という疑問について解説します。

ここまでの話を踏まえて、皆さんも一緒に考えてほしいのですが、Σ記号であらわした和と等差数列の和の公式

$$\small S_n=\frac{(2a+(n-1)d)n}{2}$$

や、等比数列の和の公式

$$\small S_n=\frac{a(r^n-1)}{r-1}$$

は一体何が違うでしょうか？

答えは、等差数列や等比数列の和の公式は、具体的な和の計算結果を求める公式ですが、一方でΣ記号は足し算の式そのものを表す記号であり具体的な計算結果ではないということです。

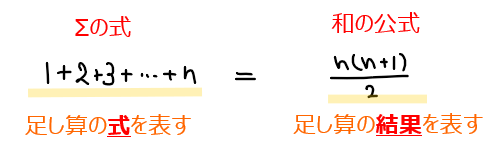
例えば等差数列の和の公式は、初項$\small a$、公差$\small d$の等差数列で初項から第$\small n$項目までの和$\small S_n$は

$$\small S_n=\frac{(2a+(n-1)d)n}{2}$$

と表せる、ということを言っています。上記の公式に初項や公比、第何項までの和を求めるかの数字を代入すれば和を求めることができますね。

もしこの等差数列の和をΣを使って表したければ、初項$\small a$、公差$\small d$の等差数列の一般項は$\small a_k=a+(k-1)d$なので、初項から第$\small n$項までの和は

$$\small \sum_{k=1}^n \{a+(k-1)d\}$$

となります。この数式が計算できるかどうかは関係なく、和をΣを使って表しただけです。ただ、等差数列の場合は、このΣの和が具体的に計算できて、$\small \displaystyle \frac{(2a+(n-1)d)n}{2}$になるというわけです。

つまり、Σと等差数列の和の公式の関係性は

$$\small \sum_{k=1}^n \{a+(k-1)d\}=\frac{(2a+(n-1)d)n}{2}$$

と表すことができます。

等比数列も同じ関係性で、

$$\small \sum_{k=1}^n ar^{k-1}=\frac{a(r^n-1)}{r-1} \space (ただしr\neq 1)$$

となります。

Point：Σ（シグマ）と和の公式の違い

・Σ（シグマ）＝足し算の式そのもののこと。
・和の公式＝足し算の計算結果のこと。

【講義5】Σの重要公式5選と覚え方

ここではΣに関する公式の中でよく使う重要な公式の覚え方を解説します。重要だけど理解していれば覚える必要がない公式もあるので、理解すべきところは理解して暗記量を減らしていきましょう。

Point：Σに関する公式5選

①　$\small \displaystyle \sum_{k=1}^n c = nc$　※$\small c$は定数
②　$\small \displaystyle \sum_{k=1}^n k = \frac{1}{2}n(n+1)$
③　$\small \displaystyle \sum_{k=1}^n k^2 = \frac{1}{6}n(n+1)(2n+1)$
④　$\small \displaystyle \sum_{k=1}^n k^3 = \left\{ \frac{1}{2}n(n+1) \right\}^2$
⑤　$\small \displaystyle \sum_{k=1}^n r^{k-1} = \frac{r^n-1}{r-1}\quad (r\neq1)$

上記の公式のうち暗記必須なのは③、④くらいです。他は暗記していなくても考え方を理解していれば自然と理解できます。

【公式①】
これは、Σで表現された足し算の式を具体的にイメージしてあげれば覚えなくても自然と計算ができます。
Σの定義に従って$\small \displaystyle \sum_{k=1}^n c$を日本語に翻訳すると、「定数$\small c$を$\small k=1$～$\small n$の範囲で足し算する」となります。
$\small k=1$のとき足し算する値は$\small c$に$\small k=1$を代入して$\small c$（$\small k$がないから代入する場所がないので、$\small c$のまま）が足し算の1番目です。同様に$\small k=2,3,\cdots n$のときも考えると足し算する値は常に$\small c$です。
結局、Σ部分を具体的な足し算の形で書き下すと
$$\small \displaystyle \sum_{k=1}^n c=c+c+c+\cdots +c$$
となり、$\small c$を$\small n$個足し算した式になるので、計算結果は$\small nc$になります。

【公式②】
これも具体的な足し算を書き下すと
$$\small \displaystyle \sum_{k=1}^n k=1+2+3+\cdots +n$$
となることから、初項1、公差1の等差数列になっています。よって、等差数列の和の公式
$$\small S_n=\frac{(初項+末項)\times 項数 \qquad}{2}$$
を使えば、初項が1、末項が$\small n$、項数が$\small n$を代入することで
$$\small S_n=\frac{(1+n)n}{2}$$
と求めることができます。

【公式③】
$\small 1～n$までの平方数（2乗）の和
$$\small 1^2+2^2+3^2+\cdots+n^2$$
の関する公式です。正直公式を暗記するのがおすすめです。
余裕がある人は、図形的な導出方法 [*1]を理解しておけば、
\begin{split}
&\small (1箇所あたりの和) \times (個数) ÷ 3\\
&\small =(2n+1)\times \frac{n(n+1)}{2}\times \frac{1}{3}\\
&\small =\frac{n(n+1)(2n+1)}{6}\\
\end{split}
と解釈できるので暗記の負荷を減らせます。

【公式④】
$\small 1～n$までの立方数（3乗）の和
$$\small 1^3+2^3+3^3+\cdots+n^3$$
の関する公式です。これも導出方法が面倒なので公式を暗記しましょう。よく形を見ると②の公式の2乗になっているので覚えやすいです。

【公式⑤】
Σの式を書き下すと
$$\small 1+r+r^2+r^3+\cdots+r^{n-1}$$
となるので、これは初項1、公比$\small r$の等比数列の和になっています。なので、等比数列の和の公式
$$\small \displaystyle a+ar+ar^2+\cdots + ar^{n-1}=\frac{a(r^n-1)}{r-1}$$
を覚えていれば、わざわざΣの公式として暗記する必要はありません。

*1：【補足】平方数の和の図形的な導出方法
下図のように1段目には「1」が書かれたボールを1個、2段目には「2」が書かれたボールを2個、3段目には「3」が書かれたボールを3個、三角形状に並べることを考えます。

ここでボールに書かれた数字の合計を計算してみましょう。各段（横）ごとに合計を求めると上から順に、$\small \color{red}{1(=1^2)}$, $\small \color{blue}{2+2=2\times 2=4(=2^2)}$, $\small \color{green}{3+3+3=3\times 3=9(=3^2)}$となり、平方数になっています。

よって、ボールに書かれた数字の合計は
$$\small 1^2+2^2+3^2=14$$
となります。つまり、ボールに書かれた数字の合計を求めることで、平方数の和が求まることになります。

では、ボールに書かれた数字の合計を少し別の方法でも求めてみます。まず、三角形を回転させて上に「1」が書かれたボールが来る向き、右下に「1」が来る向き、左下に「1」が来る向きの3種類の並べ方を考えます。そして、これら3種類を重ねたときに、同じ位置に対応するボールの数字を足し算すると、なんとすべての位置で和が「7」になることが分かります。

合計が「7」になる箇所が全部で6個あるので、3種類を合計したときのボールの数字の合計は$\small 7\times 6=42$になります。ちなみに、6個という数字は1段目にボールが1個、2段目にボールが2個、3段目にボールが3個という各段のボールの個数の合計になっているので、計算式としては$\small 1+2+3=6$のように求められます。これはΣ公式②そのものです。
最後にもともと求めたかったのは、ボールに書かれた数字の合計（1つ分）だったので、42は3種類分の合計になっているので、3で割り算した$\small 42÷3=14$が$\small 1^2+2^2+3^2$の和になります。

この考え方を一般の$\small n$の場合に当てはめると、3種類の並べ方をしたときの1箇所あたりの和は、どの箇所でも同じになるので一番考えやすい1段目に着目すると、$\small 1+n+n=2n+1$になります。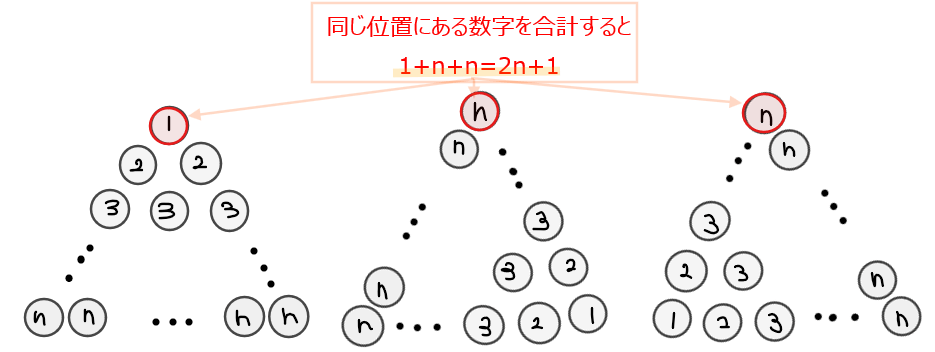

これがボールの個数だけあるわけですが、ボールの個数は各段のボールの個数の合計ですから、$\small \displaystyle 1+2+\cdots +n=\frac{n(n+1)}{2}$（公式②）になります。
よって、3種類の並べ方をしたときのボールに書かれた数字の合計は
$$\small (2n+1)\times\frac{n(n+1)}{2}=\frac{n(n+1)(2n+1)}{2}$$
です。最後に、重複している3で割り算することで
$$\small \frac{n(n+1)(2n+1)}{2}÷3=\frac{n(n+1)(2n+1)}{6}$$
となり、公式③が導出できます。

【例題付き】Σ（シグマ）の計算方法を徹底解説

【演習問題】公式を用いたΣ計算のコツ

【演習問題】公式を用いたΣ計算

次の和を求めよ。
（1）$\small \displaystyle \sum_{k=1}^{n}(2k^2+k-2)$
（2）$\small \displaystyle \sum_{k=1}^{n}(2\cdot 3^k)$

問題解決のKey

【多項式のΣ（シグマ）計算】
・分配法則を利用して公式を適用せよ！

【等比数列のΣ（シグマ）計算】
・指数部分のズレは積を分解して調整せよ！

　（1）解説

分配法則を用いて各項ごとにΣを分解すると、

\begin{split}
&\small \sum_{k=1}^n(2k^2+k-2)\\
&\small =2\sum_{k=1}^n k^2 + \sum_{k=1}^n k- \sum_{k=1}^n 2 \space \color{#ef5350}{◀公式③②①の利用}\\
&\small =2 \cdot \frac{1}{6}n(n+1)(2n+1)+\frac{1}{2}n(n+1)-2n\\
&\small =\frac{1}{3}n(n+1)(2n+1)+\frac{1}{2}n(n+1)-2n\\
\end{split}

あとは計算するだけですが、Σの計算では大体、公式をあてはめた後の式が分数になるため、分数の式を一つにまとめる作業が結構大変で、苦戦している人も多いでしょう。

分数にまとめるときのコツは大きく以下の2つです。

Point：分数計算のコツ

・コツ①：分母は通分する。
・コツ②：分子は共通因数で括る。

この2点を意識しながら計算を進めていきます。

\begin{split}
\small (与式) &\small =\frac{1}{3}n(n+1)(2n+1)+\frac{1}{2}n(n+1)-2n\\
&\small =\frac{\color{magenta}2n(n+1)(2n+1)+\color{magenta}3n(n+1)-\color{magenta}{12}n}{\color{magenta}6} \space \color{magenta}{◀【コツ①】通分}\\
&\small =\frac{\color{magenta}n\{2(n+1)(2n+1)+3(n+1)-12\}}{6} \space \color{magenta}{◀【コツ②】共通因数}\\
&\small =\frac{n\{\color{magenta}{2(2n^2+3n+1)+3n+3-12}\}}{6} \space \color{magenta}{◀残った項は展開してまとめる}\\
&\small =\frac{n\{\color{magenta}{4n^2+6n+2+3n+3-12}\}}{6}\\
&\small =\color{red}{\frac{1}{6}n(4n^2+9n-7) \space \cdots 【答】}\\
\end{split}

　（2）解説

まずは、Σの変数 $\small k$に関係ない数字（定数）をΣの外に出すことで、考える式をシンプルにしましょう。

今回であれば

\begin{split}
\small \displaystyle \sum_{k=1}^n (2\cdot 3^k)=2 \color{#ef5350}{\sum_{k=1}^n 3^k}\\
\end{split}

のように定数「2」をΣの和の外に出しておきます。上記の式は公式⑤の等比数列の和に非常によく似ていますが、よく見ると$\small 3^k$の指数部分が公式とは若干異なっています。

Σ公式⑤（再掲）
$$\small \sum_{k=1}^n r^{k-1}=\frac{r^n-1}{r-1}$$
$\small r=3$とすると、左辺が$\small \displaystyle \sum_{k=1}^n 3^{k-1}$となり、指数部分が$\small 3^k$とは異なっています。

指数がズレていると公式が使えないかというと、少し工夫してあげれば公式の形に変形することができます。

$\small 3^k$とは、そもそもの定義に立ち返ると3が$\small k$回かけ算されているという意味なので、$\small 3^k=3\times 3^{k-1}$（3が$\small k$個ある掛け算を、1個と$\small k-1$のかけ算に分解）と分解できます。

よって、

\begin{split}
&\small \displaystyle 2 \sum_{k=1}^n 3^k\\
&\small \displaystyle =2 \sum_{k=1}^n \color{#ef5350}{3\cdot 3^{k-1}}\\
&\small \displaystyle =2 \cdot \color{#ef5350}3 \sum_{k=1}^n 3^{k-1} \space \color{#ef5350}{◀定数を外だし}\\
&\small \displaystyle =6 \cdot \color{#ef5350}{\frac{3^n-1}{3-1}}\space \color{#ef5350}{◀公式⑤の利用}\\
&\small \displaystyle =6 \cdot \frac{3^n-1}{2}\\
&\small \displaystyle =\color{red}{3(3^n-1) \space \cdots 【答】}\\
\end{split}

【補足】
最後の答えは、展開して$\small 3^{n+1}-3$と答えても正解です。