【数列（数B）】漸化式の解き方（指数型、多項式型、3項間漸化式）【漸化式マスターの道②】

今回は、いよいよ漸化式の中でも受験対策レベルの難問の解き方を解説していきます。この記事では漸化式の基礎知識はすでに学習済の前提で解説していくので、もし基本問題の解き方に不安を感じる人がいれば、まず初めに以下の記事を確認してからこちらの問題にチャレンジするとよいとかと思います。

受験でよく出る漸化式問題はたくさんありますが、その中で今回取り上げるのは、指数型漸化式、多項式型漸化式、3項間漸化式です。これらの問題は解き方の発想を覚えておけば、割と簡単に基本編で学んだ漸化式の基本形に帰着させることができるので、ぜひこの記事で考え方と解き方をマスターしていきましょう。

　本記事のゴール

$\small a_{n+1}=pa_n+qr^n$型の漸化式が解けるようになること
$\small a_{n+1}=p(a_n)^q$型の漸化式が解けるようになること
多項式型（$\small a_{n+1}=pa_n+\alpha n+\beta$など）の漸化式が解けるようになること
3項間漸化式（$\small a_{n+2}+pa_{n+1}+qa_n+r=0$）が解けるようになること

　本記事はこんな人におすすめ

漸化式の問題パターンを把握したい！
パターンごとに解き方のコツが知りたい！
漸化式の問題を解いて自分の実力をチェックしたい！

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

【問題＆解説】受験頻出の漸化式問題
本記事のまとめ

【問題＆解説】受験頻出の漸化式問題

【問題1】指数型漸化式①【$\small a_{n+1}=pa_n+qr^n$型】

問題1：$\small a_{n+1}=pa_n+qr^n$型（指数型①）

$\small a_1=1$、$\small a_{n+1}=2a_n+3^n (n=1,2,3,\cdots)$によって定められる数列$\small \{a_n\}$の一般項を求めよ。

■指数型漸化式①【$\small a_{n+1}=pa_n+qr^n$型】とは？
・指数（$\small \color{magenta}{r^n}$）が含まれた漸化式のこと

■指数型漸化式①【$\small a_{n+1}=pa_n+qr^n$型】の攻略法
・式全体を$\small r^n$で割り算して$\small \displaystyle \frac{a_n}{r^n}、\frac{a_{n+1}}{r^{n+1}}$の形を作れば、
　漸化式の標準形【$\small a_{n+1}=pa_n+q$型】に帰着できる。

　解説

$\small a_{n+1}=2a_n+3^n$の両辺を$\small 3^n$で割り算すると

\begin{split}
\frac{a_{n+1}}{\color{magenta}{3^n}}&=2\cdot\frac{a_n}{\color{magenta}{3^n}}+\color{magenta}1\\
\color{blue}{3}\cdot\frac{a_{n+1}}{\color{blue}{3^{n+1}}}&=2\cdot\frac{a_n}{3^n}+1 \qquad \color{blue}{\small ◀\mathsf{分母分子に}3\mathsf{を掛け算}}\\
\end{split}

ここで$\small \displaystyle \color{magenta}{b_{n}=\frac{a_n}{3^n}}$とおくと、上式は

\begin{split}
3\color{magenta}{\fbox{$\small b_{n+1}$}}&=2\color{magenta}{\fbox{$\small b_n$}}+1 \qquad \color{magenta}{◀\small b_{n+1}=\frac{a_{n+1}}{3^{n+1}}}\\
b_{n+1}&=\frac{2}{3}b_n+\frac{1}{3} \space \cdots①\\
\end{split}

式①は漸化式の標準形【$\small a_{n+1}=pa_n+q$型】となっているので、以降は頑張って解くだけ！

●OnePoint
特性方程式の解を式①をもとに$\small \displaystyle \alpha=\frac{2}{3}\alpha+\frac{1}{3}$として解いてもよいが、その前の式を使っても同じ答えになる（ただ3で割っただけだから）ので楽な方を選びましょう。

●解法のポイント
等比数列を解くときに分かりにくければ、$\small b_{n}-1$を$\small c_n$などとおき、$\small \displaystyle \color{red}{c_{n+1}=\frac{2}{3}c_n}$として解いてもOK

数列$\small \{b_n-1\}$は等比数列で、

\begin{split}
(\mathbf{初項})&=\color{magenta}{b_1}-1\\
&=\color{magenta}{\frac{a_1}{3}}-1\qquad \color{magenta}{◀\text{$\small \displaystyle b_{n}=\frac{a_n}{3^n}$}\mathsf{を利用}}\\
&=\frac{1}{3}-1\\
&=-\frac{2}{3}\\
\end{split}

公比が$\small \displaystyle \frac{2}{3}$であることから

\begin{split}
\color{magenta}{b_n-1}&=-\frac{2}{3}\left( \frac{2}{3} \right)^{n-1}\quad \color{magenta}{◀\small \{b_n-1\}\mathsf{が等比数列であることに注意}}\\
b_n&=-\frac{2}{3}\left( \frac{2}{3} \right)^{n-1}+1\quad \cdots②
\end{split}

最後に、$\small \displaystyle b_{n}=\frac{a_n}{3^n}$に②を代入することで

\begin{split}
\frac{a_n}{3^n}&=-\frac{2}{3}\left( \frac{2}{3} \right)^{n-1}+1\\
a_n&=-\frac{2}{3}\left( \frac{2}{3} \right)^{n-1}\times 3^n+3^n\\
a_n&=\color{magenta}{-\frac{2}{3} \times \frac{2^{n-1}}{3^{n-1}} \times 3^n}+3^n\quad \color{magenta}{◀\mathrm{第一項目の}\small 3^n\mathrm{部分を整理していく}}\\
a_n&=\color{magenta}{-\frac{2^{n}}{3^{n}}\times 3^n}+3^n\\
a_n&=\color{magenta}{-2^{n}}+3^n\\
\end{split}

●解答
　$\small \color{red}{a_n=3^n-2^{n}}$

【問題2】指数型漸化式②【$\small a_{n+1}=p(a_n)^q$型】

問題2：$\small a_{n+1}=p(a_n)^q$型（指数型②）

$\small a_1=1$、$\small a_{n+1}=2\sqrt{a_n} (n=1,2,3,\cdots)$によって定められる数列$\small \{a_n\}$の一般項を求めよ。

■指数型漸化式②【$\small a_{n+1}=p(a_n)^q$型】とは？
・$\small a_n$のべき乗が含まれた漸化式のこと

■指数型漸化式②【$\small a_{n+1}=p(a_n)^q$型】の攻略法
・対数（log）をとって指数を消去。
　対数の底は、係数（$\small q$）や初項（$\small a_1$）の数字で決める。

　解説

$\small \color{red}{a_n>0}$なので、両辺を2を底とするlogをとると

\begin{split}
\log_2 a_{n+1}&=\log_22+\log_2 \sqrt{a_n}\\
\log_2 a_{n+1}&=\frac{1}{2}\log_2 a_n+1\quad \color{magenta}{◀ \small \log_2\sqrt{a_n}=\log_2(a_n)^{\frac{1}{2}}=\frac{1}{2}\log_2 a_n}\\
\end{split}

●OnePoint
logをとるときには、$\small \log_2 x$の真数$\small x$は$\small \color{red}{x>0}$を満たす必要がある（真数条件）点に注意する。
今回の$\small a_n$は値がマイナスになることがないことは漸化式からすぐにわかるので、解答欄には特に理由までは書かず、$\small a_n>0$程度でよいでしょう。

$\small \color{red}{b_n=\log_2a_n}$とおくと、

\begin{split}
\color{magenta}{ \fbox{$\small \log_2 a_{n+1}$}}&=\frac{1}{2}\color{magenta}{\fbox{$\small \log_2 a_n$}}+1\\
\color{magenta}{b_{n+1}}&=\frac{1}{2}\color{magenta}{b_{n}}+1 \quad \color{magenta}{◀ \small b_{n+1}=\log_2 a_{n+1}}\\
b_{n+1}-2&=\frac{1}{2}(b_n-2)\quad\color{magenta}{◀\mathsf{特性方程式の利用}}\\
\end{split}

●補足：特性方程式の計算と検算方法
$\small \displaystyle b_{n+1}=\frac{1}{2}b_{n}+1$は漸化式の標準形【$\small a_{n+1}=pa_n+q$型】なので特性方程式$\small \displaystyle \alpha=\frac{1}{2}\alpha+1$を解くことで、$\small \alpha=2$を得るため、上式のように式変形できる。実際に変形した式を展開し$\small \displaystyle b_{n+1}=\frac{1}{2}b_{n}+1$になることを確認することで検算できる。

$\small \color{red}{c_n=b_n-2}$とおくと、与式は

\begin{split}
\color{magenta}{\fbox{$\small b_{n+1}-2$}}&=\frac{1}{2}\color{magenta}{\fbox{$\small (b_n-2)$}}\\
\color{magenta}{c_{n+1}}&=\frac{1}{2}\color{magenta}{c_{n}}\qquad\qquad\color{magenta}{◀\small \mathsf{等比数列型}(a_{n+1}=ra_n)の漸化式}\\
c_{n}&=c_1\left(\frac{1}{2}\right)^{n-1}\quad \cdots①\\
\end{split}

初項$\small c_1$は、

\begin{split}
c_1&=b_1-2\quad\cdots②\\
b_1&=\log_2a_1 \qquad \qquad \color{magenta}{◀\small b_{n}=\log_2a_n}\\
&=0 \quad \cdots③ \qquad \quad \color{magenta}{◀\small a_1=1、\log_2 1 =0}\\
∴\space \space \color{red}{c_1}&=0-2=\color{red}{-2} \quad \quad \color{magenta}{◀\mathbf{②に③を代入}}\\
\end{split}

なので、①に代入することで、

\begin{split}
c_{n}&=(-2)\cdot\left(\frac{1}{2}\right)^{n-1}\\
c_{n}&=-\left(\frac{1}{2}\right)^{n-2}\\
\end{split}

$\small \color{red}{c_n}=b_n-2=\color{red}{\log_2a_n-2}$より

\begin{split}
\log_2a_n-2&=-\left(\frac{1}{2}\right)^{n-2}\\
\log_2a_n&=2-\left(\frac{1}{2}\right)^{n-2}\\
\displaystyle \color{red}{a_n}&\color{red}{=2^{2-\left(\frac{1}{2}\right)^{n-2}}}\quad \color{magenta}{◀\small 公式 \space 『\log_2 a=●』 → 『a=2^●』 \space を利用}\\
\end{split}

●解答
　$\small \displaystyle \color{red}{a_n=2^{2-\left(\frac{1}{2}\right)^{n-2}}}$

●検算してみよう
検算として答えの式に$\small n=1$を代入すると、
\begin{split}
\displaystyle a_1&=2^{2-\left(\frac{1}{2}\right)^{1-2}}\\
\displaystyle &=2^{2-\left(\frac{1}{2}\right)^{-1}}\\
\displaystyle &=2^{2-\color{magenta}2} \quad \color{magenta}{◀\small \left(\frac{1}{2}\right)^{-1}=2}\\
\displaystyle &=1\\
\end{split}
となり、問題文の$\small a_1=1$とも一致していることが確認できる。時間があれば、さらに答えの式に$\small n=2$を代入した値が、漸化式から求まる$\small a_2=2\sqrt{a_1}=2$と一致することを確認するとよい。

【問題3】多項式型漸化式（$\small a_{n+1}=pa_n+\alpha n+\beta$など）

問題3：多項式型（$\small a_{n+1}=pa_n+\alpha n+\beta$）

$\small a_1=1$、$\small a_{n+1}=2a_n+n+1(n=1,2,3,\cdots)$によって定められる数列$\small \{a_n\}$の一般項を求めよ。

■多項式型漸化式とは？
・『$\small a_{n+1}=pa_n+\color{magenta}{\fbox{\(\small\alpha n+\beta$}}\)』のように多項式が含まれた漸化式のこと

■多項式型漸化式の攻略法
①引き算消去法（地道な解法）　※勝手に命名…
・$\small \color{magenta}{n→n+1}$に置き換えて引き算することで、
　漸化式の標準形【$\small a_{n+1}=pa_n+q$型】に帰着させる

②裏技的解法
・$\small \color{magenta}{b_n=a_n+\alpha n +\beta}$とおくことで、等比数列型の漸化式に帰着させる

●OnePoint：多項式とは？
　$\small n^2-2n+5$ や $\small 3n+1$ など、『$\small n$の●乗』を含んだ式のこと。逆に、指数関数（$\small p^n$など）や分数関数（$\small \displaystyle \frac{pn+q}{\alpha n+\beta}$など）が出てきたら多項式型ではないと判断してOK。

多項式型の漸化式の解き方には、Pointで記載したような2つの解法があります。それぞれの解き方について、考え方とおすすめポイントを解説するので、自分が理解しやすい方法を選ぶとよいでしょう。

【解法①】引き算消去法

■引き算消去法の考え方
・多項式の$\small n$の項がなければ漸化式の標準形【$\small a_{n+1}=pa_n+q$型】になることに着目し、$\small n→n+1$に置き換えた漸化式を引き算することで解く手法

■メリットとデメリット
・解法として覚えておくべきは、漸化式を$\small n→n+1$に置き換えて引き算するという方針くらいなので、手順の暗記が簡単。
・計算量が多くなるため、時間がかかる、計算ミスの可能性が高まるのが難点。

　解説

問題の漸化式を $\small a_{n+1}=2a_n+n+1\cdots①$とする。

①の漸化式で$\small n→n+1$と置き換えると、$\small a_{\color{red}{n+2}}=2a_{\color{red}{n+1}}+\color{red}{(n+1)}+1$、→$\small a_{n+2}=2a_{n+1}+n+2\cdots②$。

②-①より

ただし最後は、$\small \color{red}{b_n=a_{n+1}-a_n\cdots③}$とおいてます。

引き算の結果、$\small b_{n+1}=2b_n+1$は漸化式の標準形【$\small a_{n+1}=pa_n+q$】になっているので、あとはひたすら頑張って計算していくだけです。

\begin{split}
\color{magenta}{b_{n+1}+1}&=2(\color{magenta}{b_n+1}) \quad \color{magenta}{\small ◀特性方程式 \alpha=2\alpha+1 を利用}\\
\color{magenta}{c_{n+1}}&=2\color{magenta}{c_n}\qquad \quad \color{magenta}{\small ◀c_n=b_n+1\cdots④と置き換え}
\end{split}

漸化式の形から$\small c_n$は、初項が$\small c_1$、公比が2の等比数列なので、

\begin{split}
c_n=c_1\cdot2^{n-1}
\end{split}

●初項$\small c_1$の計算
③、④から$\small \color{red}{c_1}=b_1+1=\color{red}{a_{2}-a_1+1}\cdots(*)$。
問題から$\small \color{red}{a_1=1}$。$\small a_2$は、問題の漸化式から
\begin{split}
\small \color{red}{a_2}=2a_1+1+1=\color{red}4
\end{split}
と求まるので、式$\small (*)$に代入することで、$\small c_1=4-1+1=\color{red}4$。

よって、

\begin{split}
c_n&=4\cdot2^{n-1}\\
\color{magenta}{b_n+1}&=4\cdot2^{n-1}\qquad \quad \color{magenta}{\small ◀式④:c_n=b_n+1}\\
b_n&=4\cdot2^{n-1}-1\\
\color{magenta}{a_{n+1}-a_n}&=4\cdot2^{n-1}-1\quad \color{magenta}{\small ◀式③:b_n=a_{n+1}-a_n}\\
\end{split}

すると、この漸化式は階差数列型の漸化式【$\small a_{n+1}=a_{n}+f(n)$型】になります。

よってその解は、$\small n≧2$として

\begin{split}
a_n&=a_1+\sum_{k=1}^{n-1}(4\cdot2^{n-1}-1)\\
&=1+4\sum_{k=1}^{n-1}2^{n-1}-\sum_{k=1}^{n-1}1\quad \color{magenta}{\small \mathsf{◀シグマの分配法則}}\\
\end{split}

ここで

\begin{split}
\sum_{k=1}^{n-1}2^{n-1}&=\frac{1\cdot(1-2^{n-1})}{1-2}\quad \color{magenta}{\small ◀公式 \sum_{k=1}^n ar^{n-1}=\frac{a(1-r^n)}{1-r}の利用}\\
&=2^{n-1}-1\\
\sum_{k=1}^{n-1}1&=n-1\qquad \qquad \quad \color{magenta}{\small ◀公式 \sum_{k=1}^n c=cn(c\mathsf{は定数})の利用}\\
\end{split}

より

\begin{split}
a_n&=1+4\cdot(2^{n-1}-1)-(n-1)\\
&=4\cdot2^{n-1}-n-2\\
&=\color{magenta}{2^{n+1}}-n-2\qquad \qquad \color{magenta}{\small ◀4\cdot2^{n-1}=2^2\cdot2^{n-1}=2^{n+1}で整理}\\
\end{split}

上記の式に$\small n=1$を代入すると、$\small a_1=2^2-1-2=1$となり問題文とも一致することから、この解は一般の$\small n=1、2、3、\cdots$に対して成立する。（階差数列なので$\small n=1$の場合にも$\small a_n$の関係式が成立しているか確認が必要）

●解答
　$\small a_n=2^{n+1}-n-2$

【解法②】裏技的解法

■裏技的解法
・$\small \color{red}{b_n=a_n+\alpha n +\beta}$とおくと等比数列の漸化式を満たすことから、漸化式と係数比較することで解く方法

■メリットとデメリット
・引き算消去法と比べて計算が圧倒的に楽。
・「$\small b_n=a_n+\alpha n +\beta$とおくと$\small b_n$が等比数列になる」という特徴を知らないと解くことができないため、解き方が特殊であり暗記が必要。

　解説

$\small \color{magenta}{b_n=a_n+\alpha n +\beta}$とおいたときに、$\small \color{magenta}{b_{n+1}=2b_n\cdots ①}$を満たすための条件を求める。

\begin{split}
b_{n+1}&=2b_n\\
a_{n+1}&+\alpha (n+1) +\beta=2(a_n+\alpha n +\beta)\quad \color{magenta}{\small ◀式①：b_n=a_n+\alpha n +\betaを利用}\\
\color{red}{a_{n+1}}&\color{red}{=2a_n+\alpha n -\alpha+\beta}
\end{split}

これが問題の漸化式、$\small a_{n+1}=2a_n+n+1$と一致する必要があるので、多項式部分を係数比較することで

\begin{split}
\begin{cases}
\color{magenta}{\alpha=1}\\
\color{blue}{-\alpha+\beta=1}
\end{cases}\\
→\alpha =1、\beta=2\\
\end{split}

この結果を$\small b_n=a_n+\alpha n +\beta$に代入して、$\small \color{red}{b_n=a_n+n +2\cdots②}$。

式①の解は、$\small b_n=b_1\cdot2^{n-1}$であり、初項$\small b_1$は

\begin{split}
\color{red}{b_1}=a_1+1+2=\color{red}4\quad \color{magenta}{\small ◀式②:b_n=a_n+n +2にn=1を代入}
\end{split}

よって、$\small b_n=4\cdot2^{n-1}=2^{n+1}$。

最後に、式②を用いることで、

\begin{split}
a_n&+n +2=2^{n+1}\\
\color{red}{a_n}&\color{red}{=2^{n+1}-n-2\quad \cdots【答】}\\
\end{split}

こんな感じで、解法①（引き算消去法）と比べてかなり計算が楽なことが分かると思います。

【問題4】3項間漸化式(特性方程式の解に1が含まれる場合)

問題4：3項間漸化式①

$\small a_1=1$、$\small a_2=2$、$\small 3a_{n+2}-4a_{n+1}+a_n=0(n=1,2,3,\cdots)$によって定められる数列$\small \{a_n\}$の一般項を求めよ。

■3項間漸化式とは？
・$\small a_n、a_{n+1}、a_{n+2}$の3つの項が出てくる漸化式のこと

■3項間漸化式（特性方程式の解＝１）の攻略法
・特性方程式の1以外の解$\small \alpha$を用いて、$\small a_{n+2}-\color{blue}{\alpha} a_{n+1}=\color{magenta}{a_{n+1}-\color{blue}{\alpha}a_{n}}=\cdots=\color{magenta}{a_{2}-\color{blue}{\alpha}a_{1}}$と変形することで、漸化式の標準形【$\small a_{n+1}=pa_n+q$型】に帰着させて解くことが可能

●OnePoint
一般に3項間漸化式は特性方程式の解$\small \alpha、\beta$を用いて
①：$\small \displaystyle a_{n+2}-\color{red}\alpha a_{n+1}=\color{blue}{\beta}(a_{n+1}-\color{red}\alpha a_n)$
②：$\small \displaystyle a_{n+2}-\color{blue}\beta a_{n+1}=\color{red}{\alpha}(a_{n+1}-\color{blue}\beta a_n)$
の2通りに式変形ができます（これは覚えておきましょう）。特性方程式の解に1が含まれる場合は、$\small \displaystyle a_{n+2}-\color{blue}\alpha a_{n+1}=(a_{n+1}-\color{blue}\alpha a_n)$となる式変形を選ぶことで、公比が1の等比数列（つまりすべての項が同じ数列）になるため、
\begin{split}
a_{n+1}-\alpha a_{n}&=a_{2}-\alpha a_1=q(定数)\\
a_{n+1}&=\alpha a_{n}+q\\
\end{split}
となり、漸化式の標準形【$\small a_{n+1}=pa_n+q$型】に帰着させることができます。
※$\small \displaystyle a_{n+2}-a_{n+1}=\alpha(a_{n+1}-a_n)$と変形した漸化式を使っても解くことができますが、一般的に階差数列となるため、計算が煩雑になります。

　解説

まずは、特性方程式を解いていきます（解答には記載不要）。

\begin{split}
3\alpha^2-4\alpha+1&=0\\
(3\alpha-1)(\alpha-1)&=0\\
\Rightarrow\space \alpha=\color{red}1,\color{blue}{\dfrac{1}{3}}
\end{split}

この2解から、等比数列を以下のように2通りで設定できますが、ポイントに記載の通り、漸化式の標準形にして解く方が簡単なので、設定方法①のように式変形した漸化式を使っていきます。

●設定方法①：$\small \displaystyle a_{n+2}-\color{blue}{\frac{1}{3}}a_{n+1}=\color{red}1\cdot(a_{n+1}-\color{blue}{\frac{1}{3}}a_n)$　☚おすすめ
●設定方法②：$\small \displaystyle a_{n+2}-\color{red}1\cdot a_{n+1}=\color{blue}{\frac{1}{3}}(a_{n+1}-\color{red}1\cdot a_n)$

問題の漸化式、$\small 3a_{n+2}-4a_{n+1}+a_n=0$は、$\small \displaystyle a_{n+2}-\frac{1}{3}a_{n+1}=a_{n+1}-\frac{1}{3}a_n $と式変形でき、

\begin{split}
a_{n+2}-\frac{1}{3}a_{n+1}&=\color{magenta}{a_{n+1}-\frac{1}{3}a_n} \quad \cdots①\\
&\color{magenta}{=a_{n}-\frac{1}{3}a_{n-1}}\\
&\begin{bmatrix}
\small 式①でn→n-1に置き換えた漸化式\quad\\
\color{magenta}{\small a_{n+1}-\frac{1}{3}a_{n}=a_{n}-\frac{1}{3}a_{n-1}}を利用\quad \\
\end{bmatrix}\\
&\quad \vdots\\
&\quad \vdots\\
&=a_{2}-\frac{1}{3}a_{1}\quad \color{magenta}{\small ◀式①を繰り返し利用}\\
&=2-\frac{1}{3}\cdot1\\
&=\frac{5}{3}\\
\end{split}

よって、$\small \displaystyle a_{n+1}-\frac{1}{3}a_n=\frac{5}{3}$となります。

●OnePoint：公比1の等比数列の計算
上記の式変形が分かりにくければ、$\small \displaystyle b_n=a_{n+1}-\frac{1}{3}a_n$とおいて考えてみましょう。このように置き換えると式①は、
\begin{split}
b_{n+1}&=b_n \quad\cdots (*)\\
\end{split}
とシンプルになります。この式は$\small n+1$項目と$\small n$項目の値が同じであるということを意味しているので、端的に日本語化するならば、「隣り合う項の値が同じ」ということになります。

ということは、1項目と2項目が同じで、2項目と3項目も同じ、3項目と4項目も同じで、…、$\small n-1$項目と$\small n$項目が同じで、$\small n$項目と$\small n+1$項目が同じということ。結局、全部の項が同じということになります。

これは、式$\small (*)$の漸化式を見ても明らかで、この式は、$\small n$の値をずらしていくことで、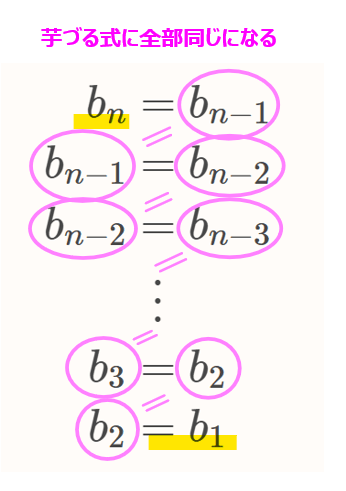

となり、結局、$\small b_{n}=b_1$となります。

よって、置き換えていた数列をもとに戻してあげれば、
\begin{split}
a_{n+1}-\frac{1}{3}a_n&=a_{2}-\frac{1}{3}a_1\\
&=\frac{5}{3}
\end{split}
となり、同じ結果になります。ごちゃごちゃした数列は慣れるまでは置き換えをして見やすくすると分かりやすくなるのでおすすめです。

$\small \displaystyle a_{n+1}-\frac{1}{3}a_n=\frac{5}{3}$は、ちょっと式変形してあげれば、$\small \displaystyle a_{n+1}=\frac{1}{3}a_n+\frac{5}{3}$となり、漸化式の標準形【$\small a_{n+1}=pa_n+q$型】となるので、通常の2項間漸化式として計算ができます。

\begin{split}
a_{n+1}&=\frac{1}{3}a_n+\frac{5}{3}\\
a_{n+1}-\frac{5}{2}&=\frac{1}{3}\left(a_n-\frac{5}{2}\right)\quad\color{magenta}{\small ◀特性方程式の解が\alpha=\frac{5}{2}}\\
\end{split}

$\small \displaystyle b_n=a_n-\frac{5}{2}$とおくと、$\small \displaystyle \color{magenta}{b_1}=a_1-\frac{5}{2}=1-\frac{5}{2}\color{magenta}{=-\frac{3}{2}}$より、

\begin{split}
a_{n+1}-\frac{5}{2}&=\frac{1}{3}\left(a_n-\frac{5}{2}\right)\\
b_{n+1}&=\frac{1}{3}b_n\\
b_{n}&=-\frac{3}{2}\left(\frac{1}{3}\right)^{n-1}\\
a_n-\frac{5}{2}&=-\frac{3}{2}\left(\frac{1}{3}\right)^{n-1}\quad\color{magenta}{◀\small \displaystyle b_n=a_n-\frac{5}{2}}\\
∴\space \color{red}{a_n}&\color{red}{=-\frac{3}{2}\left(\frac{1}{3}\right)^{n-1}+\frac{5}{2}\cdots【答】}\\
\end{split}

●解答
$\small \displaystyle \color{red}{a_n}\color{red}{=-\frac{3}{2}\left(\frac{1}{3}\right)^{n-1}+\frac{5}{2}}$

【問題5】3項間漸化式（特性方程式の解≠1の場合）

問題5：3項間漸化式②

$\small a_1=2$、$\small a_2=3$、$\small a_{n+2}-2a_{n+1}-3a_n=0(n=1,2,3,\cdots)$によって定められる数列$\small \{a_n\}$の一般項を求めよ。

■3項間漸化式（特性方程式の解≠1）の攻略法
・STEP1：3項間漸化式を、特性方程式の2つの異なる解を$\small \alpha、\beta$として
　　　　　①：$\small \displaystyle a_{n+2}-\color{red}\alpha a_{n+1}=\color{blue}{\beta}(a_{n+1}-\color{red}\alpha a_n)$
　　　　　②：$\small \displaystyle a_{n+2}-\color{blue}\beta a_{n+1}=\color{red}{\alpha}(a_{n+1}-\color{blue}\beta a_n)$
　　　　　と式変形
・STEP2：①，②の2つの等比数列を解く。
・STEP3：STEP2で求めた解を連立させて、$\small a_n$のみの形に変形

　解説

特性方程式、$\small \alpha^2-2\alpha-3=0$を解くことで得られる解、$\small \alpha =-1,3$から、問題の漸化式は

\begin{cases}
a_{n+2}-\color{red}{(-1)}\cdot a_{n+1}&=\color{blue}3\cdot(a_{n+1}-\color{red}{(-1)}\cdot a_{n})\\
a_{n+2}-\color{blue}3\cdot a_{n+1}&=\color{red}{(-1)}\cdot(a_{n+1}-\color{blue}3\cdot a_{n})\\
\end{cases}

\begin{split}
\Rightarrow \space
\begin{cases}
\color{magenta}{a_{n+2}+a_{n+1}}&=3(\color{magenta}{a_{n+1}+a_{n}})\quad \cdots①\\
\color{magenta}{a_{n+2}-3a_{n+1}}&=-(\color{magenta}{a_{n+1}-3a_{n}})\quad \cdots②\\
\end{cases}
\end{split}

①は初項が$\small a_{2}+a_{1}=\color{red}5$、公比が3の等比数列なので、

\begin{split}
a_{n+1}+a_{n}&=5\cdot 3^{n-1}\quad \cdots①’\\
\end{split}

また、②は初項が$\small a_{2}-3a_{1}=\color{red}{-3}$、公比が-1の等比数列なので、

\begin{split}
a_{n+1}-3a_{n}&=(-3)\cdot(-1)^{n-1}\quad \cdots②’\\
\end{split}

①’-②’より

\begin{split}
4a_{n}&=5\cdot 3^{n-1}+3\cdot(-1)^{n-1}\\
\Rightarrow \space \color{red}{a_{n}}&\color{red}{=\frac{5\cdot 3^{n-1}+3\cdot(-1)^{n-1}}{4}\cdots【答】}\\
\end{split}

●解答
$\small \displaystyle a_{n}=\frac{5\cdot 3^{n-1}+3\cdot(-1)^{n-1}}{4}$

【問題6】3項間漸化式（特性方程式の解が重解の場合）

問題6：3項間漸化式③

$\small a_1=0$、$\small a_2=4$、$\small a_{n+2}-4a_{n+1}+4a_n=0(n=1,2,3,\cdots)$によって定められる数列$\small \{a_n\}$の一般項を求めよ。

■3項間漸化式（重解）の攻略法
・特性方程式の重解を$\small \alpha $として、$\small \displaystyle a_{n+2}-\alpha a_{n+1}=\alpha(a_{n+1}-\alpha a_n)$と変形
・等比数列を解くことで、指数型漸化式①【$\small a_{n+1}=pa_n+qr^n$型】に帰着

　解説

特性方程式を解くと

\begin{split}
\alpha^2 &-4\alpha+4=0\\
&(\alpha-2)^2=0\\
& ∴ \space \alpha =2
\end{split}

問題の漸化式は、特性方程式の解を使うことで、

$$a_{n+2}-2a_{n+1}=2(a_{n+1}-2a_{n})$$

と表せることから、数列$\small \{a_{n+1}-2a_{n}\}$は初項が$\small a_2-2a_1=\color{red}4$、公比が2の等比数列になるので

\begin{split}
a_{n+1}-2a_{n}&=4\cdot2^{n-1}\\
∴\space a_{n+1}-2a_{n}&=2^{n+1}
\end{split}

上記の漸化式は、指数型漸化式①【$\small a_{n+1}=pa_n+qr^n$型】になっていることに注目！

あとは、指数型漸化式①の方法で解いきましょう。

両辺を$\small 2^{n+1}$で割り算すると

\begin{split}
\frac{a_{n+1}}{2^{n+1}}-2\cdot \frac{a_{n}}{2^{n+1}}&=1\\
\frac{a_{n+1}}{2^{n+1}}-\frac{a_{n}}{2^{n}}&=1\\
\end{split}

$\small \displaystyle b_n=\frac{a_{n}}{2^{n}}$とおくと、上記漸化式は

\begin{split}
b_{n+1}-b_n&=1\quad \color{magenta}{◀\small 等比数列 b_{n+1}=b_n+1の漸化式}
\end{split}

となるので、数列$\small \{b_n\}$は、初項が$\small \displaystyle b_1=\frac{a_1}{2}=\color{green}{0}$、公差が1の等差数列であることから、

\begin{split}
b_{n}&=0+(n-1)\cdot 1 \\
b_{n}&=n-1\\
\end{split}

よって、

\begin{split}
\frac{a_{n}}{2^{n}}&=n-1 \quad \color{magenta}{◀\small b_n=\frac{a_{n}}{2^{n}} とおいていた}\\
∴\space \color{red}{a_n}&\color{red}{=2^{n}(n-1)\quad \cdots【答】}\\
\end{split}

●解答
　$\small \color{red}{a_n=2^{n}(n-1)}$

本記事のまとめ

今回は漸化式問題の定番問題として押さえておきたいパターンを徹底解説していきました。

●本記事で扱った問題
・$\small a_{n+1}=pa_n+qr^n$型の漸化式　【問題1】
・$\small a_{n+1}=p(a_n)^q$型の漸化式　【問題2】
・多項式型（$\small a_{n+1}=pa_n+\alpha n+\beta$など）の漸化式　【問題3】
・3項間漸化式（$\small a_{n+2}+pa_{n+1}+qa_n+r=0$）　【問題4】【問題5】【問題6】

いろいろなパターンが出てきたので、改めて「この問題の解き方ってどんなんだっけ？」と思った人は、リンクから攻略法を確認しておきましょう。

今回の問題パターンをおさえておけば受験対策はある程度問題ないと思いますが、さらに漸化式を極めたい人向けの難問集を次回は作成する予定ですので、アップロードされましたらぜひ確認してみてください。

では今回は以上です。お疲れ様でした！