【領域における最大最小】円・直線・放物線で囲まれた領域の最大最小の見分け方！基本問題～応用問題を徹底解説

今回は、円、直線、放物線で囲まれた領域における最大値や最小値の求め方について解説していきます。「最大最小の問題なのに、なんでグラフが出てくるの？」、「グラフをかいて最大最小を求める解き方がよくわからない…」、「問題演習を通して自分自身の理解度をチェックしたい！」など領域における最大最小の問題に関する悩みを一つずつ解決できる記事になっていると思うので、ぜひ最後まで読んでみてください！

　本記事はこんな人におすすめ

グラフのどの部分で最大値、最小値になるのか分からない…
グラフの傾きや切片など、どこに注目すればいいのか分からない…
分かりやすくて丁寧な解説がほしい…
問題のパターンや解き方のコツを知りたい…
ちょっと難しめの問題にも挑戦して自分の実力をチェックしたい！

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

【はじめに】領域における最大最小の求め方
【領域における最大最小】基本問題5選
【領域における最大最小】応用問題2選
1. 問題6：分数型の最大最小
2. 問題7：特殊な領域における最大最小
まとめ

【はじめに】領域における最大最小の求め方

はじめに、領域における最大最小の求め方について、問題の基本パターンと解き方を紹介します。

■よく出る領域の形3パターンの組み合わせ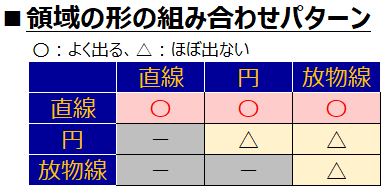

■よく出る求める式の形4パターン
　・直線型　：$\small x+y$などの1次式
　・円型　　：$\small x^2+y^2$など
　・放物線型：$\small x^2-y$など
　・分数型　：$\small \displaystyle \frac{x+y}{x+2}$など分数の形になっている

■基本の解き方4ステップ
　・STEP1：求める式の図形的な意味を確認
　　　　　　→$\small k$とおいて直線型/円型/放物線型/分数型のどれに当てはまるか確認
　・STEP2：領域を図示
　　　　　　→不等式の範囲を図示
　・STEP3：最大、最小となる点を特定
　　　　　　→図形的な問題に言い換えてみる
　・STEP4：最大値、最小値を求める
　　　　　　→$\small x,y$の値を代入して$\small k$の値を求める

上記の内容について、領域における最大最小の考え方や解き方を基礎から知りたいという人は、「【領域における最大最小】解き方の基本（例題＋線形計画法の解説付き）」の記事で詳しく解説しているので、先に読んでから今回の問題にチャレンジすると、より理解しやすくなると思います！

【領域における最大最小】基本問題5選

基本問題5選

(1) 不等式 $\small x^2+y^2≦4,\space y≧0$を満たす$\small x, y$に対して、$\small x-2y$ の最大値、最小値を求めよ。

(2) 不等式 $\small x-y+2≧0,\space x+2y+4≧0,\space 3x-y-4≦0$ を満たす$\small x, y$に対して、$\small x^2+y^2$ の最大値、最小値を求めよ。

(3) 不等式 $\small x^2+y^2≦1,\space y≧x$を満たす$\small x, y$に対して、$\small x^2+y^2-4x$ の最大値、最小値を求めよ。

(4) 不等式 $\small y≦-x^2+4, \space y≧x+2$を満たす$\small x, y$に対して、$\small x^2+y^2$ の最大値、最小値を求めよ。

(5) 不等式 $\small x^2+y^2≦4,\space y≧x$を満たす$\small x, y$に対して、$\small x^2-y$ の最大値、最小値を求めよ。

ではそれぞれの問題について解説していきます。

直線型の最大最小

問題1：円と直線で囲まれた領域における最大最小

直線型の最大最小（円と直線で囲まれた領域）

不等式 $\small x^2+y^2≦4,\space y≧0$を満たす$\small x, y$に対して、$\small x-2y$ の最大値、最小値を求めよ。

■最大・最小を求めるときの注意点
$\small k$にマイナス符号が付く場合、求める値の最大最小とグラフの位置関係の関係性が逆転するので気をつけろ！

　解説

求める式を$\small x-2y=k$とおくと、$\small \color{green}{y=\frac{1}{2}x-\frac{k}{2}}$となり、傾き$\small \frac{1}{2}$、切片$\small -\frac{k}{2}$の直線になります。

ここで、求める式の値$\small k$の最大最小と考えるときの注意点として、切片$\small -\frac{k}{2}$は$\small k$の前にマイナス符号がついているため、求める式の値$\small k$が最大のとき、直線のグラフ自体は最も下側に位置することになります。逆に、求める式の値$\small k$ が最小となるときは、直線のグラフは最も上側に位置することになります。

kの値が-2から4に大きくなるほど
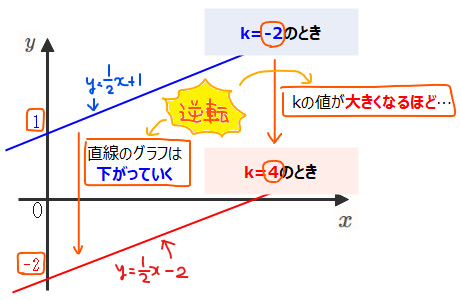
直線のグラフの切片が小さくなり、下がっていく

このように、$\small k$の前にマイナス符号がついているときには、求める値の最大・最小とグラフの位置関係のイメージが逆転するので注意しましょう。

本題にもどり、$\small x^2+y^2≦4,\space y≧0$の領域を図示すると、上半円内部になります（下図の黄色部分（境界を含む））。

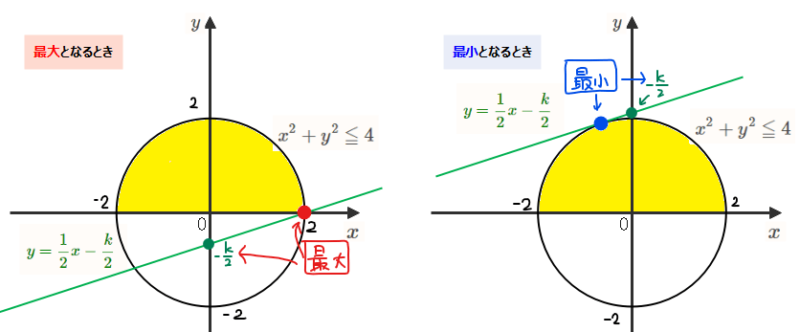
今回の問題を図形的な問題に言い換えると「黄色い領域を通る傾き$\small \frac{1}{2}$の直線を引くときに、切片が一番高いところと低いところはどこか？」となります。

すると、求める式の形から傾き$\small \frac{1}{2}$の直線を上下に動かして切片の範囲を確認すると左図のときが切片が最も小さくなる（＝$\small k$が最大）、右図のときが切片が最も大きくなる（＝$\small k$が最小）であることが分かります。

[1]最大となるとき
左図のときは、点$\small (2,0)$を通る直線となることから、$\small x=2,y=0$なので、求める式の値は、$\small x-2y=2-0=2 \cdots①$

[2]最小となるとき
右図のときは、直線$\small \color{green}{y=\frac{1}{2}x-\frac{k}{2}}$ と円$\small x^2+y^2=4$ が接する点（青色の点）を通ります。直線の式と円の方程式を連立して2次方程式の解が重解(D=0)を利用して求めてもよいですが計算が大変なので、直線と円が接するとき、「（直線と円の中心との距離）＝（半径）」となることを利用します。

すると、直線$\small y=\frac{1}{2}x-\frac{k}{2}$ ⇔ $\small \color{green}{x-2y-k=0}$と原点の距離が2になることから、点と直線の距離の公式より
\begin{equation}
\begin{split}
\frac{|0-2\cdot0-k|}{\sqrt{1^2+(-2)^2}}&=2\\
\frac{|k|}{\sqrt{5}}&=2\\
|k|&=2\sqrt{5}\\
k&=\pm 2\sqrt{5}\\
\end{split}
\end{equation}

ここで$\small k$の値ですが、図から切片$\small -\frac{k}{2}>0$なので、$\small k<0$となり、$\small k=-2\sqrt{5}$が適した解となります。

求める式を$\small k$としていたので、これが$\small x-2y$の最小値です。

（解答）
最小値は$\small -2\sqrt{5}$, 最大値は$\small 2$.

円型の最大最小

問題2：直線で囲まれた領域における最大最小

円型の最大最小（直線で囲まれた領域）

不等式 $\small x-y+2≧0,\space x+2y+4≧0,\space 3x-y-4≦0$ を満たす$\small x, y$に対して、$\small x^2+y^2$ の最大値、最小値を求めよ。

　解説

$\small x^2+y^2=k$とおくと、求める式は原点を中心とした半径$\small \sqrt{k}$の円を表します(ただし、$\small k≧0$)。

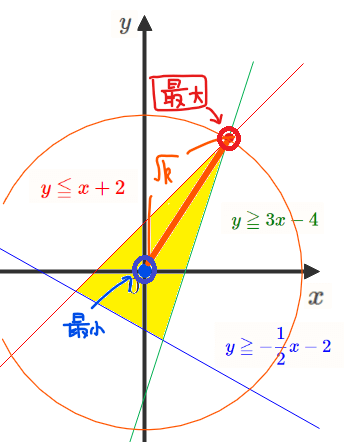
それぞれの不等式を$\small xy$平面上に図示すると下図の黄色部分（境界を含む）となります。

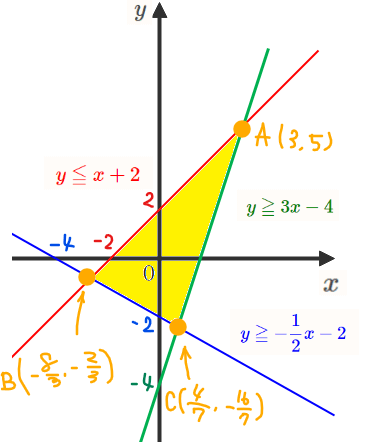
今回考える問題を図形的な問題に言い換えると、「黄色い領域を通って中心(0,0)、半径$\small \sqrt{k}$の円の半径が一番短くなるときと長くなるときを求めよ」となります。

すると、図から半径が最小となるのは円の半径＝ゼロ（=原点）のときです。一方、黄色い部分に触れながら円の半径を最大にしようと考えると、原点から一番距離が離れている点A$\small (3,5)$を通る円になることがわかります。

よって、解答をまとえると以下の通りです

（解答）
$\small x=0,y=0$のとき$\small x^2+y^2$は最小値0をとり、$\small x=3,y=5$のとき$\small x^2+y^2$は最大値34.

問題3：円と直線で囲まれた領域における最大最小

円型の最大最小（円と直線で囲まれた領域）

不等式 $\small x^2+y^2≦1,\space y≧x$を満たす$\small x, y$に対して、$\small x^2+y^2-4x$ の最大値、最小値を求めよ。

■最大・最小となる点の座標が具体的にわからないとき
求める座標を文字で置いて数式的に求める！
「図から何となく」や「感覚に頼る」のは危険！

　解説

求める式を$\small x^2+y^2-4x=k$とおくと、$\small x^2+y^2$があるので円の方程式になりそうです。少し式変形をしてみると、

$$
\begin{equation}
\begin{split}
x^2-4x\color{red}{+4}+y^2&=k\color{red}{+4}\\
\color{red}{(x-2)^2}+y^2&=k+4\quad \cdots①\\
\end{split}
\end{equation}
$$

となり、点$\small (2,0)$を中心とする半径$\small \sqrt{k+4}$の円であることが分かります。

今回考える領域については、問題文の不等式から、原点を中心とする半径1の円の内側（$\small x^2+y^2≦1$）かつ直線$\small y=x$の上側（$\small y≧x$）の部分になります（下図の黄色部分（境界を含む））。

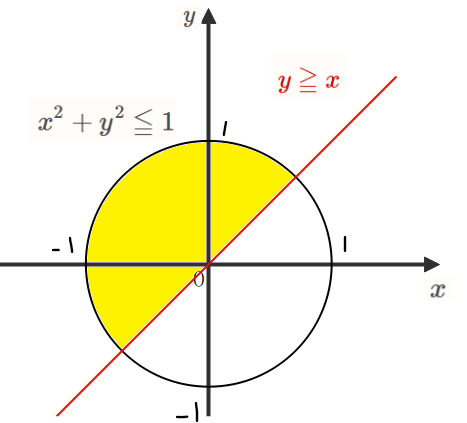
最大最小となる点の特定については、今回の問題文を図形的な問題に置き換えると「黄色い領域を通って中心(2,0)、半径$\small \sqrt{k+1}$の円の半径が最も長くなるときと最も短くなるときを求めよ」となります。

よって、それぞれ考えると下図のようなイメージになります。

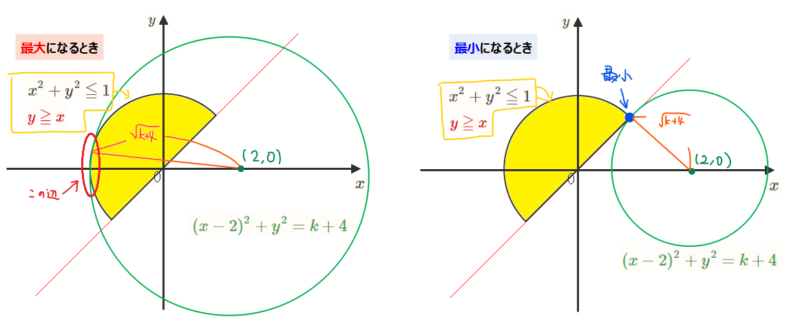
”イメージ”と書いたのは、最大となるときは赤丸で囲った部分あたりということまでは分かりますが、正確にどの点で半径が最大になるかはぱっとは分からなかったので、そういう場合はしっかり計算で求めていきます。くれぐれも「ここでしょ！」と早合点しないように注意しましょう。

半径$\small \sqrt{k+1}$が最大となる点の座標から求めていきます。求める座標を$\small (p,q)$とおくと、円$\small x^2+y^2=1$上の点であることは分かっているので、

$$\color{red}{p^2+q^2=1 \quad \cdots②}$$

すると下図のオレンジ色の三角形で三平方の定理をつかうことで

\begin{equation}
\begin{split}
(2-p)^2+q^2&=(\sqrt{k+4})^2\\
4-4p+\color{red}{p^2+q^2}&=k+4\\
4-4p+\color{red}{1}&=k+4\\
k&=-4p+1 \quad \cdots③\\
\end{split}
\end{equation}

ただし、赤字箇所は式②の関係を用いています。

ここで、$\small p$の存在範囲を考えてみます。

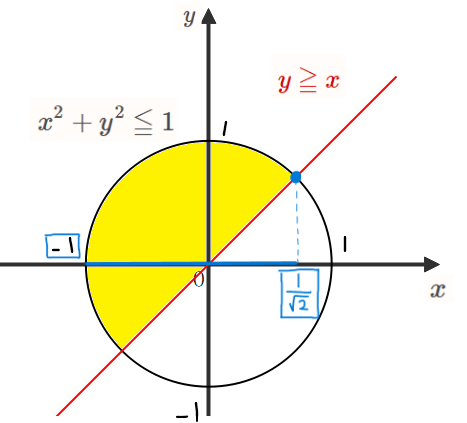
$\small p$は求める座標の$\small x$座標の値なので上図の通り一番左端は-1(円の左端)で、一番右端は円$\small x^2+y^2=1$と直線$\small y=x$の交点なので、連立させることで$\small x$座標が求められて

\begin{equation}
\begin{split}
x^2+\color{red}y^2&=1\\
x^2+\color{red}x^2&=1\\
2x^2&=1\\
x=&\pm\frac{1}{\sqrt{2}}\\
\end{split}
\end{equation}

図から、$\small x>0$なので、$\small \displaystyle x=\frac{1}{\sqrt{2}}$が一番右端の$\small x$座標と分かります。つまり、$\small p$の存在範囲は

$$\color{red}{-1≦p≦\frac{1}{\sqrt{2}}\quad \cdots④}$$

となります。$\small k$の存在範囲を求めるために、④の不等式を③の形になるように式変形していくと

\begin{equation}
\begin{split}
-1≦&p≦\frac{1}{\sqrt{2}}\\
\color{blue}{(-4)}\cdot \frac{1}{\sqrt{2}}≦&\color{blue}{(-4)}p≦\color{blue}{(-4)}\cdot(-1)\\
-2\sqrt{2}\color{red}{+1}≦&-4p\color{red}{+1}≦4\color{red}{+1}\\
-2\sqrt{2}+1≦&k≦5\\
\end{split}
\end{equation}

$\small k$が求める式の値だったので、それが$\small \color{red}{-2\sqrt{2}+1≦k≦5}$であることから、最大値は$\small 5$、最小値は$\small -2\sqrt{2}+1$であることが分かります。

最大値を求めるはずが、最小値まで一気に求めることができちゃいましたね。

ここでは解説は割愛しますが、最小値については、最小値をとる青点の座標$\small \left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$を$\small x^2+y^2-4x$に代入する方法でも求めることができます。

（解答）
最大値は5, 最小値は$\small -2\sqrt{2}+1$.

問題4：直線と放物線で囲まれた領域における最大最小

円型の最大最小（直線と放物線で囲まれた領域）

不等式 $\small y≦-x^2+4, \space y≧x+2$を満たす$\small x, y$に対して、$\small x^2+y^2$ の最大値、最小値を求めよ。

　解説

まずは$\small x^2+y^2=k$とおき、今回求める式の形が原点を中心とした半径$\small \sqrt{k}$の円だということを確認します。

次に領域を確認します。$\small y≦-x^2+4$は「$\small y≦\cdots$」なので放物線の下側、$\small y≧x+2$は「$\small y≧\cdots$」なので直線の上側を指していることから、下図の黄色部分が不等式の表す領域になります。

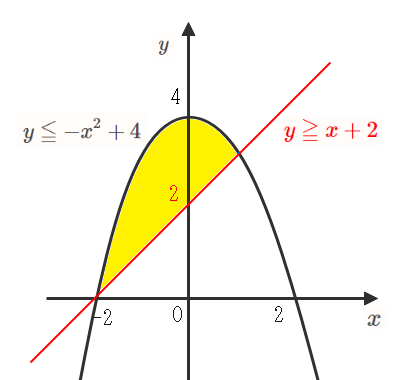
では、ここで今回の問題を図形的な問題に言い換えると、「黄色部分を通って、原点中心の円の半径が最も長くなるときと最も短くなるときを求めよ」ということができます。

それぞれをグラフで表すと下図の通りです。

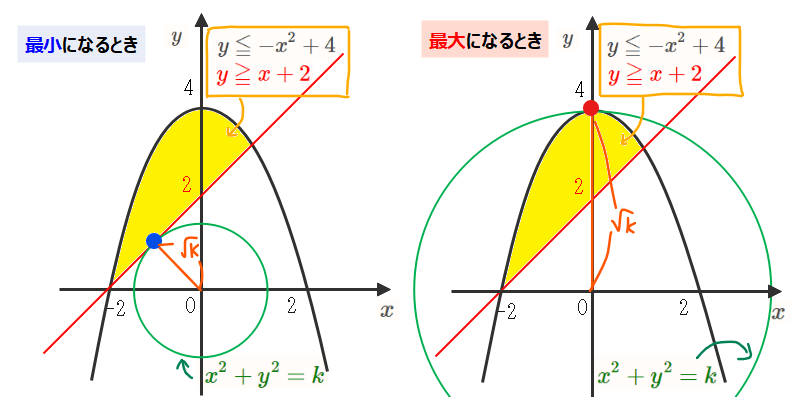
[1]最小になるとき
上左図のように、緑の円の半径が最小になるのは、円が直線 $\small y=x+2$（$\small x-y+2=0$）に接するときなので、原点と直線 $\small x-y+2=0$の距離が$\small \sqrt{k}$になることから
\begin{equation}
\begin{split}
\frac{|\color{red}0-\color{red}0+2|}{\sqrt{1^2+(-1)^2}}&=\sqrt{k}\\
\sqrt{k}&=\sqrt{2}\\
k&=2\\
\end{split}
\end{equation}
よって、最小値は$\small 2$となります。

[2]最大になるとき
黄色い領域の中で原点と最も離れているのは図より点(0,4)なので、$\small x=0,\space y=4$を求める式に代入することで、$\small x^2+y^2=\color{red}0^2+\color{red}4^2=\color{red}{16}$が最大値になります。

（補足）原点から一番離れている点は本当に点(0,4)なのか？
気になる人は、問題3のようにしっかり計算することで求めることができます。
最も離れている点は放物線上の点になるので$\small (p,-p^2+4)$とおけます。ただし、黄色の範囲しか動けないので$\small p$の存在範囲は$\small \color{blue}{-2≦p≦1}$です。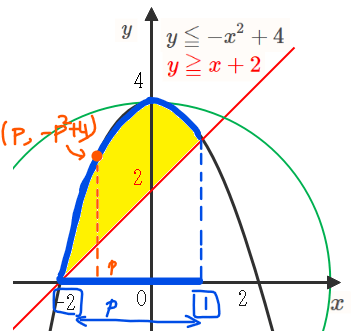

そうしたら、半径の長さ、つまり原点との距離は三平方の定理から
\begin{equation}
\begin{split}
\sqrt{p^2+(-p^2+4)^2}&=\sqrt{p^4-7p^2+16}\\
&=\sqrt{\left(p^2-\frac{7}{2}\right)^2+\frac{15}{4}}\\
\end{split}
\end{equation}
ただし、$\small 0≦p^2≦4$。よって、$\small 0≦p^2≦4$の範囲でルートの中身の最大を考えればよいので、$\small p^2=0$のとき最大になることが分かります。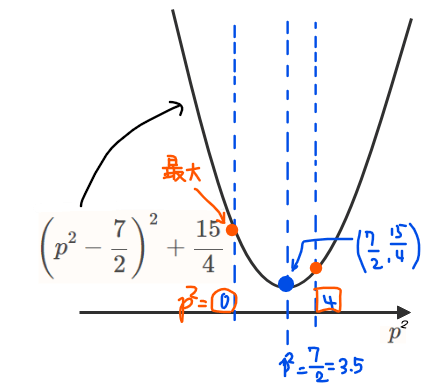

$\small p^2$のままだとわかりにくければ、$\small p^2=t$とおいて、$\small 0≦t≦4$で$\small \left(t-\frac{7}{2}\right)^2+\frac{15}{4}$の最大値を求めると考えるとわかりやすいと思います。

（解答）
最大値は16, 最小値は2.

放物線型の最大最小

問題5：円と直線で囲まれた領域における最大最小

放物線型の最大最小（円と直線で囲まれた領域）

不等式 $\small x^2+y^2≦4,\space y≧x$を満たす$\small x, y$に対して、$\small x^2-y$ の最大値、最小値を求めよ。

　解説

求める式を$\small x^2-y=k$とおくと、$\small y=x^2-k$より、求める式は切片が$\small -k$で下に凸の放物線を表していることが分かります。

不等式が表す領域は円$\small x^2+y^2≦4$の内部、直線$\small y≧x$の上側なので、図示すると以下の黄色の領域（境界を含む）になります。

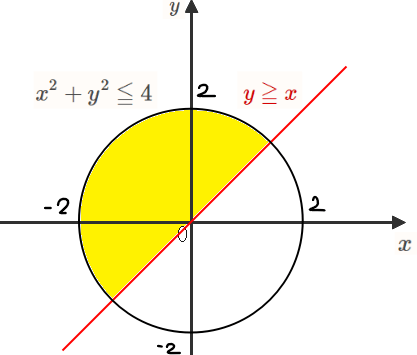
最大最小と考えるにあたって問題文を図形的な問題に言い換えると、「黄色い部分を通って、放物線$\small y=x^2-k$の切片$\small -k$が最も高くなるときと最も低くなるときを求めよ」となります。ちなみに、切片の符号がマイナスなので、切片が最大のとき求める式の値は最小で、逆に切片が最大のとき求める式の値は最小になることに注意します。

では、それぞれ最大と最小になるときの図をかいてみましょう。

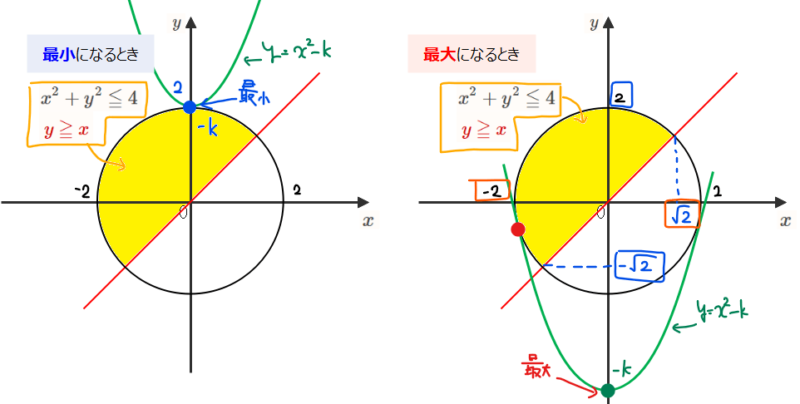
最小となる点については、左図の青点(0,2)のときが切片が最も高い（＝求める値としては最小）点となることから、$\small x=0, y=2$を$\small x^2-y$に代入することで、-2が最小値と求まります。

最大となる点については、右図の円周上の赤点箇所で放物線が円と接するときが最も切片が小さく（＝求める値としては最大に）なりそうです。このときの座標はさすがに図からは分からないので計算で求めていきます。

まずは、赤い点の座標を$\small (p,q)$とおきます。次に、$\small x^2+y^2=4$と$\small y=x$の交点の座標を求めると

\begin{equation}
\begin{split}
x^2+\color{red}x^2&=4\\
x^2&=2\\
x&=\pm \sqrt{2}\\
\end{split}
\end{equation}

より、$\small (\sqrt{2},\sqrt{2})、(-\sqrt{2},-\sqrt{2})$が交点の座標になります。赤い点は黄色い領域の円周上のどこかの点なので、図より$\small (p,q)$の取り得る値の範囲は、

\begin{equation}
\begin{split}
\color{red}{-2}&\color{red}{≦p≦\sqrt{2} \quad \cdots①}\\
\color{blue}{-\sqrt{2}}&\color{blue}{≦q≦2 \qquad \cdots②}\\
\end{split}
\end{equation}

となります。また、$\small p, q$は円周上の点なので

$$p^2+q^2=4 \quad \cdots③$$

以上の情報から、求める値$\small k$を$\small p, q$で表すと

\begin{equation}
\begin{split}
k=\color{red}{p^2}-q&=\color{red}{(4-q^2)}-q\\
&=-q^2-q+4\\
&=-(q^2+q)+4\\
&=-\left\{\left(q+\frac{1}{2}\right)^2-\frac{1}{4}\right\}+4\\
&=-\left(q+\frac{1}{2}\right)^2+\frac{17}{4}\quad \cdots⑤\\
\end{split}
\end{equation}

ただし、赤字の式変形は④の関係を使ってます。あとは、②の範囲$\small -\sqrt{2}≦q≦2$で⑤の最大値を求めればよいので、$\small q$の2次関数と考えることで、頂点の箇所$\small q=-\dfrac{1}{2}$で最大値$\small \dfrac{17}{4}$をとることが分かります。

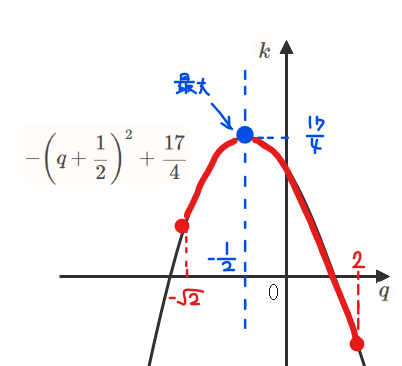
（解答）
最大値は$\small \dfrac{17}{4}$, 最小値は-2.

【領域における最大最小】応用問題2選

応用問題2選

（1）不等式 $\small x^2+y^2≦1,\space y≧0$を満たす$\small x, y$に対して、$\small \displaystyle \frac{x-y+3}{x+2}$ の最大値、最小値を求めよ。

（2）不等式 $\small y≧0,\space 1≦x^2+y^2≦4,\space y≧x$を満たす$\small x, y$に対して、$\small -2x+y$ の取り得る値の範囲を求めよ。

問題6：分数型の最大最小

分数型の最大最小（円と直線で囲まれた領域）

不等式 $\small x^2+y^2≦1,\space y≧0$を満たす$\small x, y$に対して、$\small \displaystyle \frac{x-y+3}{x+2}$ の最大値、最小値を求めよ。

■分数型の最大最小を求めるコツ
求める式を$\small k$とおいて、$\small \color{red}{y=}\color{green}{(kの式)}\color{red}{(x-a)+b}$の形に変形せよ！

　解説

$\small k=\dfrac{x-y+3}{x+2}$とおきます。「$\small y=\cdots$」の形に変形すると

\begin{equation}
\begin{split}
&k(x+2)=x-y+3\\
&y=(1-k)x\color{red}{-2k+3}\\
&y=(1-k)x\color{red}{+2(1-k)+1}\\
&\color{green}{y=(1-k)(x+2)+1\quad\cdots①}\\
\end{split}
\end{equation}

途中の赤字の式変形は、$\small x$の係数である$\small (1-k)$をうまく作り出すように変形していて、最後の式①を見ると図形的には「傾き$\small 1-k$で点(-2,1)を通る直線」を表しています。

■直線の方程式
点$\small (a,b)$を通り、傾き$\small m$の直線の方程式は
$$y=m(x-a)+b$$

分数型の場合は、必ずある点を通り傾きが$\small k$の値に依存して変わる直線の式になるので、そのことを念頭に置いて式変形を進めていくといいと思います。

問題文の領域は、半径1の円の上半分なので、下図の黄色部分（境界を含む）になります。

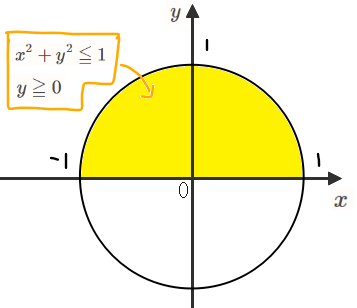
問題を図形的な問題に言い換えると、「黄色い部分を通って、点(-2,1)を通る直線の傾きが最大になるときと最小になるときを求めよ」になります。そのため、傾きがどんな範囲を動くのか確認すればよく、最大のときと最小のときはそれぞれ下図の通りになります。

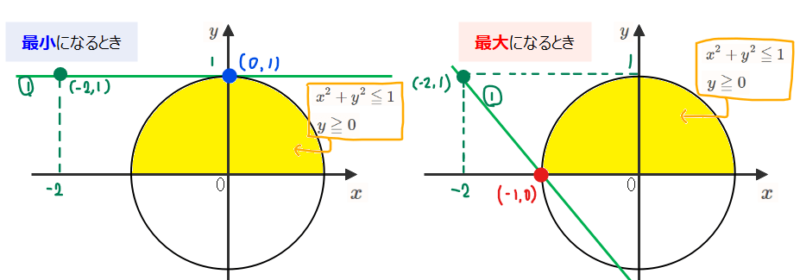
注意点としては、傾き $\small 1-k$は$\small k$にマイナス符号がついているので、「傾きが最大＝$\small k$（求める式の値）は最小」、「傾きが最小＝$\small k$（求める式の値）は最大」と最大最小が逆転します。

今回だと、左上図は傾きが0で、右上図は傾きが負なので右上図のときに傾きが最小＝求める式の値は最大といった感じです。

最小となるときは、左上図のように傾きが0になるので、$\small 1-k=0$、すなわち$\small k=1$となります（これが最小値）。

最大値については、右上図のように、点(-1,0)を通るときに傾きが最小となるときなので、$\small x=-1,\space y=0$を$\small \dfrac{x-y+3}{x+2}$に代入することで、$\small \dfrac{\color{red}{-1}-\color{red}0+3}{\color{red}{-1}+2}=2$が最大値となります。

（解答）
最大値は2, 最小値は1.

問題7：特殊な領域における最大最小

特殊な領域における最大最小

不等式 $\small y≧0,\space 1≦x^2+y^2≦4,\space y≧x$を満たす$\small x, y$に対して、$\small -2x+y$ の取り得る値の範囲を求めよ。

　解説

「取り得る値の範囲」という聞かれ方になっていますが、つまりは最大値と最小値を聞かれているので解き方は同じになります。

求める式を$\small k=-2x+y$とおくと、$\small y=2x+k$。

今回考える領域は、$\small 1≦x^2+y^2≦4$が少し難しそうに見えるかもしれませんが、$\small x^2+y^2≧1$と$\small x^2+y^2≦4$をまとめて書いているだけ（$\small x≧0, x≦2$をまとめて$\small 0≦x≦2$とかくのと同じ）なので、言語化すると原点を中心とする半径1の円の外側かつ半径2の円の内側となります。そこに、$\small y≧0$と$\small y≧x$の条件を組み合わせると下図の黄色部分(境界線を含む)になります。

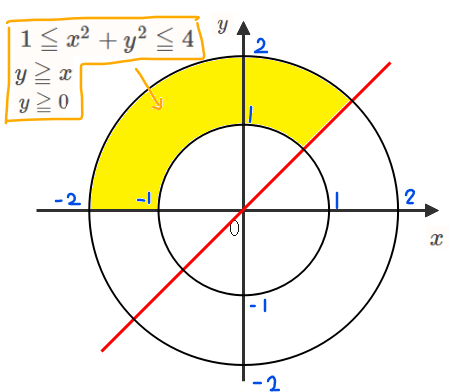
よって、図形の問題としては、「黄色い部分を通って、傾き2の直線の切片が最大になるときと最小になるときを求めよ」という問題に置き換わります。

先程の図の赤線$\small y=x$ よりも$\small y=2x+k$ の方が傾きが急であることに注意すると、最大点、最小点はそれぞれ以下の通りになります。

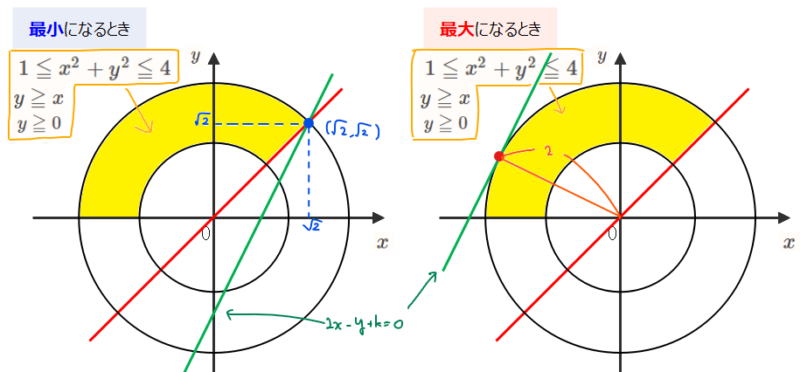
最小となるときについては、円$\small x^2+y^2=4$と直線$\small y=x$の交点である青点を通るので、連立方程式を解くことで

\begin{equation}
\begin{split}
&x^2+x^2=4\\
&2x^2=4\\
&x=\sqrt{2}\quad (∵ x≧0)\\
\end{split}
\end{equation}

$\small y=x$上の点なので、$\small y$座標も$\small \sqrt{2}$になるので、青色の点の座標は、$\small (\sqrt{2},\sqrt{2})$。よって、$\small -2x+y$に代入することで、$\small -\sqrt{2}$が最小値となります。

最大値については、円$\small x^2+y^2=4$と直線$\small y=x$が図のように接するときが切片が最大になるので、求める式$\small 2x-y+k=0$(緑の直線)と原点の距離が円の半径である2になればよいので、点と距離の公式より

\begin{equation}
\begin{split}
\frac{|2\cdot 0-0+k|}{\sqrt{2^2+(-1)^2}}&=2\\
\frac{|k|}{\sqrt{5}}&=2\\
k=&2\sqrt{5}\quad (∵ k≧0)\\
\end{split}
\end{equation}

$\small k$の値が求める式の値なので、$\small 2\sqrt{5}$が最大値です。

今回は、取り得る値の範囲を聞かれているので答えを不等式でかいてあげれば完成です。

（解答）
$$-\sqrt{2}≦-2x+y≦2\sqrt{5}$$