【図形と方程式】円と直線、放物線との共有点の個数（判別式・図形の位置関係を利用した解法を徹底解説）

今回は、円と直線、円と放物線の共有点の個数を求める問題について徹底解説していきます。

具体的な図形の方程式が分かっている場合は、グラフを描いて共有点の個数を調べることができますが、文字を含む場合は、場合分けして求める必要があります。また、共有点の求め方にも、判別式を利用して解く方法や図形的な位置関係から解く方法など複数の方法があります。

そのため、解き方や考え方が分かりにくかったり、結局どうやって解けばいいのか分からなくなることが多い分野かと思います。

そんな悩みを抱えた人向けに、本記事では、文字を含んだ図形の方程式同士の共有点の個数の求め方をパターンごとに分かりやすく解説しますので、、ぜひ最後までチェックしていきましょう！

　本記事はこんな人におすすめ

共有点の個数の求め方や解き方のコツを知りたい人
文字を含んだ共有点の個数を求める際の場合分けが苦手な人
共有点の個数を求める問題の定期テスト対策・受験対策がしたい人

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

本記事の要点
【問題＆解説】共有点の個数の求め方
【徹底解説】共有点の個数を求める問題
本記事のまとめ

本記事の要点

本記事では、共有点の個数を求める問題について解説していきますが、まずはじめに本記事の結論をお伝えします。

☆重要Point☆
・共有点の個数は一般的に、連立した方程式の解の配置問題として考えることができる。
・特に連立した式が2次方程式の場合は、判別式を利用すると簡単に求めることが可能。
・2次方程式ではない場合は、図形の位置関係で解いていき、詳細部分で数式利用。

では、上記の結論を頭の片隅に置きながら、共有点の個数の求め方について、実際の問題を通して理解を深めていきましょう。

【問題＆解説】共有点の個数の求め方

【問題1】円と直線の共有点【難易度：★】

問題1：円と直線の共有点

$\small k$を実数の定数とするとき、$\small (x-2)^2+y^2=2、x+2y-k=0$の共有点の個数を求めよ。

問題解決のKey

・共有点の個数は、2つの方程式を連立させることで得られる。
・円と直線の共有点では、連立させた結果得られる2次関数の判別式を利用するのが王道(講義2を参照)。
・ただし、円と直線の共有点の場合は、図形的な性質を利用したアプローチとして、「円の中心と直線までの距離」と「半径」の比較が効果的。

【王道】判別式を利用した解法

まずは王道の解法を解説します。

　解説

直線の方程式 $\small x+2y-k=0$を $\small y$について解くと

$$\small y=\frac{-x+k}{2}$$

これを、円の方程式 $\small (x-2)^2+y^2=2$に代入して$\small x$に関する2次方程式にすると

\begin{split}
\small (x-2)^2+\left(\frac{-x+k}{2}\right)^2 &\small =2\\
\small 4(x-2)^2+(x-k)^2 &\small =8 \quad \color{#ff6900}{◀\mathsf{両辺を}4\mathsf{倍}}\\
\small 5x^2-2(k+8)x+k^2+8 &\small =0\\
\end{split}

この2次方程式の解の個数＝共有点の個数となるため、判別式を考えることで

\begin{split}
\small \frac{D}{4}& \small =(k+8)^2-5(k^2+8)\\
\small & \small =-4k^2+16k+24\\
\end{split}

$\small x$の係数が2の倍数の場合の判別式

2次方程式の$\small x$の係数が $\small ax^2+\color{#ff6900}{2bx}+c=0$のように2の倍数の場合、判別式は
$$\small \color{#ff6900}{\frac{D}{4}=b^2-ac}$$
で求まる。
知っていると計算が楽になるのでしっかり覚えておきましょう！

よって、共有点の個数は

[1] 共有点の個数が2個になる場合
$\small \displaystyle \frac{D}{4}>0$の場合、すなわち
\begin{split}
\small -4k^2+16k+24 & \small >0\\
\small k^2-4k-6 & \small <0\\
\small ∴\space \color{#ff6900}{2-\sqrt{10}<k<2+}& \color{#ff6900}{\small \sqrt{10}}\\
\end{split}
の場合、共有点の個数は2個。

[2] 共有点の個数が1個になる場合
$\small \displaystyle \frac{D}{4}=0$の場合、すなわち、$\small \color{#ff6900}{k=2\pm\sqrt{10}}$の場合、共有点の個数は1個。

[3] 共有点の個数が0個になる場合
$\small \displaystyle \frac{D}{4}<0$の場合、すなわち、$\small \color{#ff6900}{k<2-\sqrt{10}、2+\sqrt{10}<k }$の場合、共有点の個数は0個。

（解答）
$\small 2-\sqrt{10}<k<2+\sqrt{10}$のとき、共有点の個数は2個。
$\small k=2\pm\sqrt{10}$のとき、共有点の個数は1個。
$\small k<2-\sqrt{10}、2+\sqrt{10}<k $のとき、共有点の個数は0個。

【別解】点と距離の公式を利用した解法

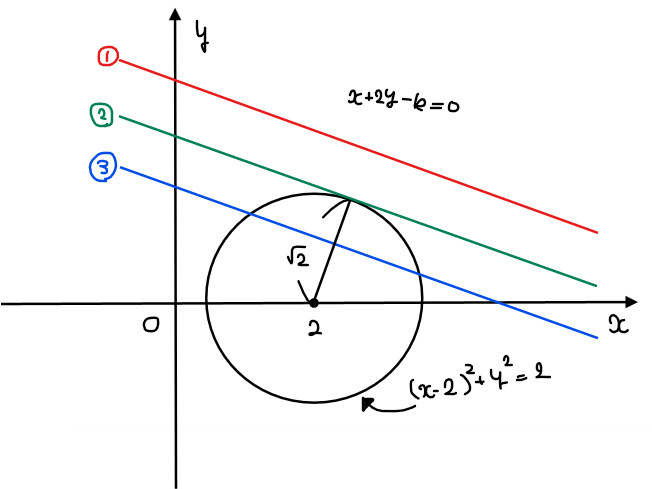
共有点の個数は、上図のような円と直線の位置関係によって、3パターンに分かれる。図を見ると明らかだが、円と直線が共有点を持つかどうかは、円の中心と直線までの距離が円の半径と比べて、①長い、②等しい、③短いによって決まる。

円の中心$\small (2,0)$と直線 $\small x+2y-k=0$の距離$\small d$は、点と距離の公式から

\begin{split}
\small d=\frac{|2-k|}{\sqrt{5}}
\end{split}

なので、半径$\small \sqrt{2}$と比較することで共有点の個数が求まる。

[1] $\small d>\sqrt{2}$の場合（冒頭図の赤線①）
\begin{split}
&\small \frac{|2-k|}{\sqrt{5}} > \sqrt{2}\\
&\small |2-k| > \sqrt{10}\\
&\small (k-2)^2 >10\\
&\small k^2-4k-6 >0\\
\small ∴\space & \small \color{#ff6900}{k<2-\sqrt{10}、2+\sqrt{10}<k}\\
\end{split}
このとき、共有点の個数は0個。

[2] $\small d=\sqrt{2}$の場合（冒頭図の緑線②）
\begin{split}
&\small \frac{|2-k|}{\sqrt{5}} = \sqrt{2}\\
&\small |2-k| = \sqrt{10}\\
&\small k-2 =\pm\sqrt{10}\\
\small ∴\space & \small \color{#ff6900}{k=2\pm \sqrt{10}}\\
\end{split}
このとき、共有点の個数は1個。

[3] $\small d<\sqrt{2}$の場合（冒頭図の青線③）
\begin{split}
&\small \frac{|2-k|}{\sqrt{5}} < \sqrt{2}\\
&\small |2-k| < \sqrt{10}\\
&\small (k-2)^2 <10\\
&\small k^2-4k-6 <0\\
\small ∴\space & \small \color{#ff6900}{2-\sqrt{10}<k<2+\sqrt{10}}\\
\end{split}
このとき、共有点の個数は2個。

●どっちの解法がおすすめ？
計算の楽さを重視するのか解法のシンプルさを重視するのかで変わってきます。

計算の楽さを求めるなら、別解で紹介した、点と距離の公式から求める方が計算量が少なくておすすめです。

一方で、点と距離の公式で解けるのは、円と直線の共有点の個数のみなので解法のシンプルさを求めるのであれば、汎用的に使える判別式を利用して解くのがよいでしょう。

【問題2】共有点を持つための条件【難易度：★★】

問題2：共有点を持つための条件

点$\small \mathrm{A}(-3,-1)$と点$\small \mathrm{B}(2,4)$を両端とする線分$\small \mathrm{AB}$と円 $\small x^2+y^2=a^2 \space (a>0)$が共有点を持つための$\small a$の値の範囲を求めよ。
[神戸薬大]

問題解決のKey

・問題1が直線との共有点だったのに対して、本問は線分との共有点である点が大きく異なる。
・線分と円の共有点の問題は、2次関数の解の配置問題に帰着できる（詳細は講義4を参照）。
　※解の配置問題について詳しく知りたい人は「【解の配置問題】2次方程式の解の存在範囲」の記事を要チェック！

　解説

2点$\small \mathrm{A}(-3,-1)$、$\small \mathrm{B}(2,4)$を通る直線の方程式は、$\small y=x+2$。ただし、線分$\small \mathrm{AB}$は、$\small -3≦x≦2$の範囲に限定されることに注意する。

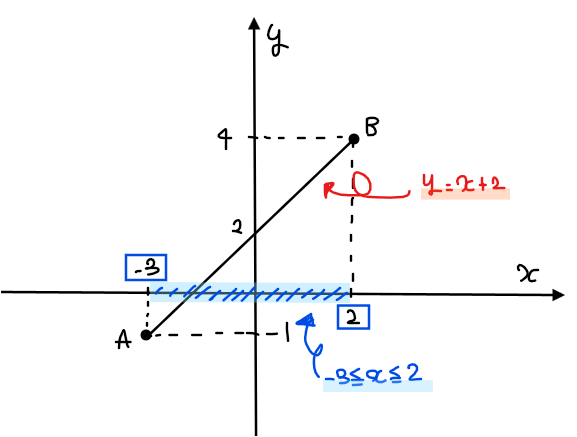
●直線と線分の違いは？
数学用語として似ているが、全然違う意味なので要注意。
直線とは、無限に伸びる線のこと。一方で、線分とは長さに限りがあるものを指す。本問では点$\small \mathrm{A}$と点$\small \mathrm{B}$を結んだ線のことなので、$\small x$の定義域も$\small -3≦x≦2$に限定されることに注意。

共有点を求めるために、円 $\small x^2+y^2=a^2$と線分$\small \mathrm{AB}$ $\small y=x+2\space (-3≦x≦2)$を連立させると

\begin{split}
&\small x^2+(x+2)^2 =a^2\\
&\small 2x^2+4x-a^2+4 =0\\
\end{split}

となる。

円と線分$\small \mathrm{AB}$が共有点を持つための条件は、『$\small -3≦x≦2$の範囲で上記の2次方程式が1つ以上の実数解を持つこと』である。

つまり、本問は2次関数の解の配置問題に帰着する。

Point：解の配置問題の解き方

・STEP1：問題を満たす2次関数のグラフを図示
・STEP2：グラフをもとに3つの観点で条件を確認
　　　　　・判別式の条件
　　　　　・軸の範囲
　　　　　・境界での$\small y$座標

●共有点を持つ条件が判別式 $\small D≧0$だけではだめな理由
2次方程式の解＝共有点の$\small x$座標なので、ただ2次方程式の判別式を解いて1つ以上の実数解があることが分かっても、その解が線分$\small \mathrm{AB}$の範囲である$\small -3≦x≦2$内の解になっているかを考える必要がある。

まずは、$\small f(x)=2x^2+4x-a^2+4$とおいて、2次関数$\small y=f(x)$のグラフを図示しておく。

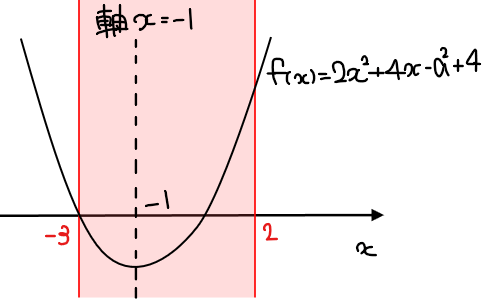
この2次関数は軸が$\small x=-1$で切片が$\small -a^2+4$なので、$\small a$の値によって上下にしか移動しないことくらいが分かっていればよいだろう。

判別式の条件は、実数解を1個以上持っていればよいので、$\small \displaystyle \frac{D}{4}≧0$より、

\begin{split}
\small \frac{D}{4}&\small =2^2-2(-a^2+4)≧0\\
\Leftrightarrow \space &\small\quad 2a^2-4≧0\\
\Leftrightarrow \space &\small \quad a≦-\sqrt{2}、\sqrt{2}≦a\\
\end{split}

問題文から、$\small a>0$の条件を加味すると、$\small \sqrt{2}≦a\space \cdots$①.

定義域の境界条件は、2次関数の性質から、軸$\small x=-1$を中心に左右対称なので、下図のようにグラフを徐々に下側にずらしていくとはじめに左側の解が定義域の左端 $\small x=-3$からはみ出て、続いて右側の解が定義域の右端 $\small x=2$からはみ出ることになる。

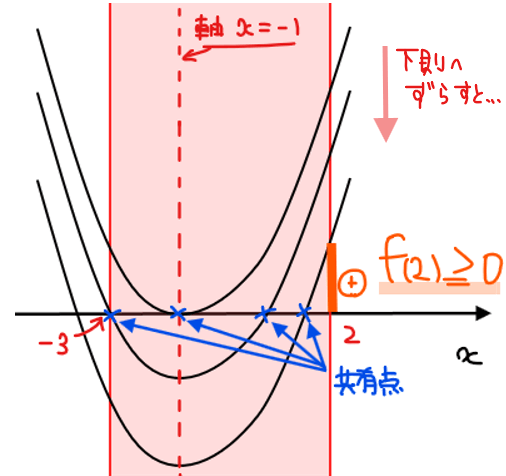
このことから、境界条件としては$\small x=-3$側の$\small y$座標については特に条件なし（$\small f(-3)$は正にも負にもなり得る）で、$\small x=2$側の$\small y$座標が0以上、すなわち$\small f(2)≧0$であれば少なくとも1つの実数解を持つことになる。

よって、

\begin{split}
\small f(2)= & \small -a^2+20≧0\quad \color{#ff7043}{\mathbf{◀}f(x)\mathbf{に}x=2\mathbf{を代入}}\\
\small \Leftrightarrow \space &\small \quad a^2≦20\\
\small ∴\space &\small -2\sqrt{5}≦a≦2\sqrt{5}\\
\end{split}

問題文から、$\small a>0$の条件を加味すると、$\small 0<a≦2\sqrt{5}\space \cdots$②.

よって、①、②の共通範囲（どちらの条件も満たさないとダメだから）を考えることで、$\small \sqrt{2}≦a≦2\sqrt{5}$ …【答】.

【問題3】円と放物線の共有点【難易度：★★★★】

問題3：円と放物線の共有点

放物線 $\small y=x^2$と円 $\small x^2+(y-a)^2=16$との共有点の個数を求めよ。ただし、$\small a$は任意の実数とする。
[中央大]

問題解決のKey

これまでと同様に、2つの方程式を連立して$\small y$を消去すると
\begin{split}
&\small x^2+(x^2-a)^2=16\\
&\small x^4+(-2a+1)x^2+a^2-16=0\\
\end{split}
となり、$\small x$に関する4次方程式になってしまうため、判別式が使えない…。
※判別式は2次方程式の場合のみ有効（講義3も併せてチェック！）

このような場合は、図形的なアプローチで解いていき、詳細な部分を数式的に解く合わせ技で考えるとよい。

　解説

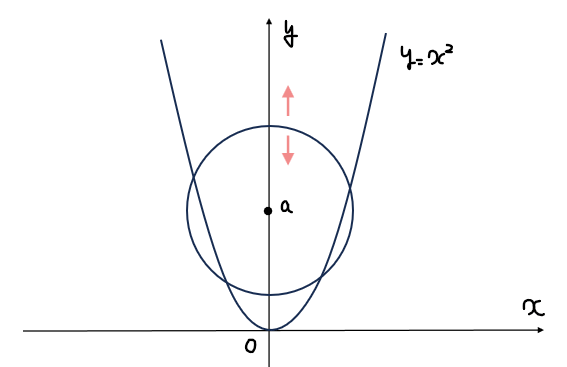
問題にある放物線と円のグラフは上図の通り。円の方程式は中心座標が$\small (0,a)$なので、$\small a$の値にのよって$\small y$軸上を上下に移動する。

円と放物線の図形的な位置関係から、共有点の個数は以下の7パターンに絞り込めることが分かる。

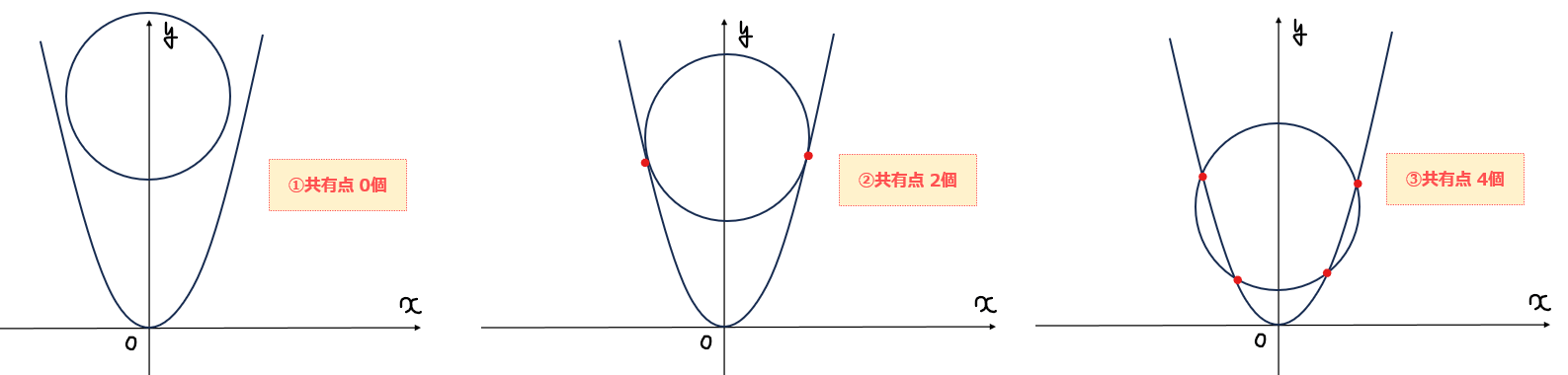
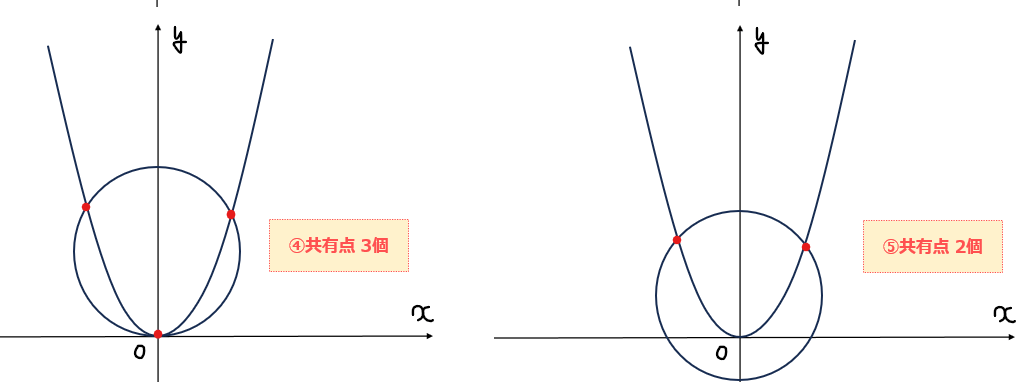
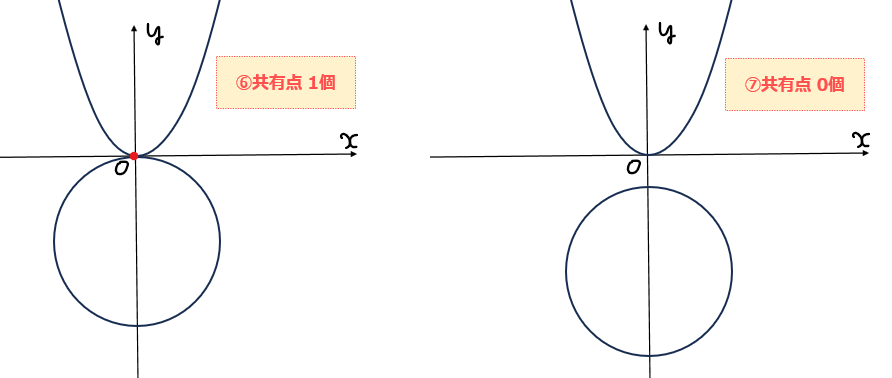
この中で、②、④、⑥は円と放物線の位置関係がちょうど図の位置にあるときしか成り立たないのでこのときの$\small a$の値から求めていく。

まず簡単なところから求めていくと、④は円の下端が原点に接しているパターンなので、円の中心＝半径の位置にあることが分かるので、$\small a=4$。よって、$\small a=4$のとき共有点は3個…②。

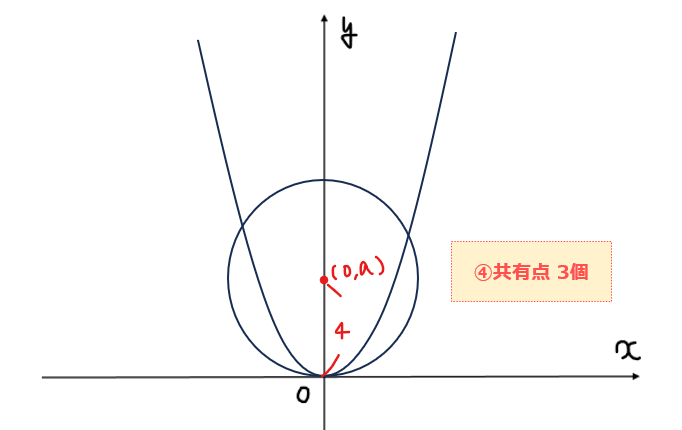
次に、⑥の場合も同様に考えると、円の上端が原点と接しているので、$\small a=-4$のとき共有点は1個…⑥。

②のパターンは円が放物線の内側で2点と接するパターンだが、図形的なアプローチだけではすぐにわかりそうにない。そのため、数式的なアプローチで考えてみる。

まず、円と放物線の方程式を連立させたいのだが、$\small y$を消去すると$\small x$に関する4次方程式になってしまいややこしいので、$\small x$の方を消去すると

\begin{split}
&\small y+(y-a)^2=16\\
&\small y^2+(-2a+1)y+a^2-16=0\\
\end{split}

これであれば、2次方程式なので判別式が使える。円と放物線が接するときには「判別式=0」となるので、

\begin{split}
\small D &\small =(-2a+1)^2-4(a^2-16)=0\\
&\small \Leftrightarrow \space 4a^2-4a+1-4a^2+64=0\\
& \small \Leftrightarrow \space a=\frac{65}{4}\\
\end{split}

よって、$\small \displaystyle a=\frac{65}{4}$のとき共有点は2個…②。

●判別式=0で接点なのか？
少し上級者向けの細かい話なので、一旦解き方がわかればOKという人はここは飛ばしてもらって大丈夫です。

ここでは次のような疑問に対して補足します。
2次方程式 $\small y^2+(-2a+1)y+a^2-16=0$で「判別式=0」の条件で分かるのは、$\small y$の実数解が1個、すなわち共有点の$\small y$座標が1つということなので、接点以外にも下図のようなパターン⑤の場合も含まれるのでは？という疑問です。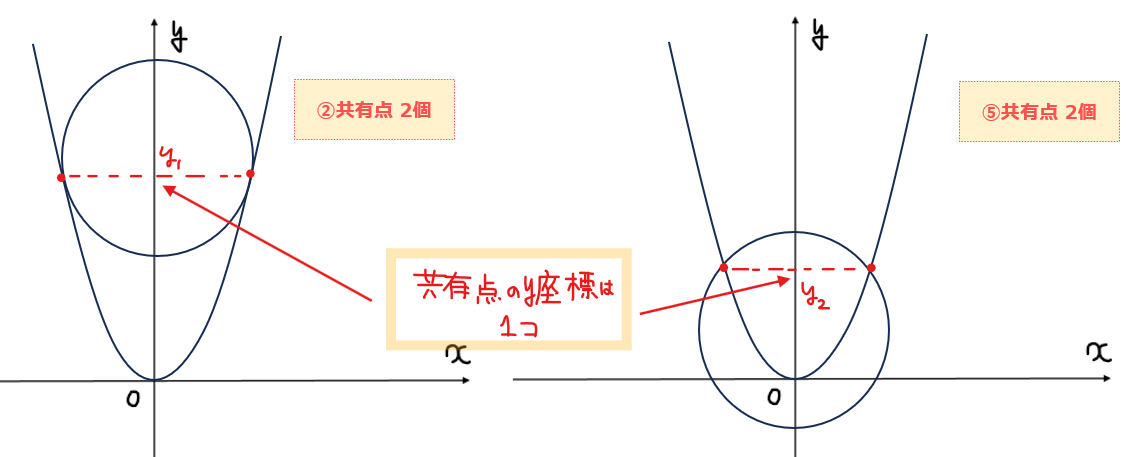

ここに疑問を感じた人は、結構数学的なセンスが鋭いなぁと思います！確かに一見すると両方のパターンが含まれそうですが、パターン⑤の場合は、2次方程式を解くとしっかり2つの実数解が出てきます。ただ、片方の解は$\small y<0$となるので、$\small y=x^2$の値域が$\small y≧0$に合致せず不適となり、結果1つの解だけが選ばれるわけです。
なので、判別式=0（重解）の場合は接点になります。

②、④、⑥の結果から、7パターンごとの$\small a$の範囲が求めることができる。

例えば、パターン③であれば、②$\small \displaystyle \left(a=\frac{65}{4}\right)$の状態から円を下にスライドして④$\small \displaystyle (a=4)$に到達するまでの範囲であり、$\small a$は円の中心の$\small y$座標だったので、$\small \displaystyle 4<a<\frac{65}{4}$となる。

他のパターンについても同様に計算すると

パターン①：$\small\displaystyle a>\frac{65}{4}$のとき共有点は0個
パターン②：$\small \displaystyle a=\frac{65}{4}$のとき共有点は2個
パターン③：$\small \displaystyle 4<a<\frac{65}{4}$のとき共有点は4個
パターン④：$\small \displaystyle a=4$のとき共有点は3個
パターン⑤：$\small \displaystyle -4<a<4$のとき共有点は2個
パターン⑥：$\small \displaystyle a=-4$のとき共有点は1個
パターン⑦：$\small \displaystyle a<-4$のとき共有点は0個

よって、共有点の個数ごとに整理したものが答えとなる。

（解答）
$\small \displaystyle a>\frac{65}{4}、a<-4$のとき共有点は0個、
$\small \displaystyle a=-4$のとき共有点は1個、
$\small \displaystyle -4<a<4、a=\frac{65}{4}$のとき共有点は2個、
$\small \displaystyle a=4$のとき共有点は3個、
$\small \displaystyle 4<a<\frac{65}{4}$のとき共有点は4個

●数式的に解く方法はないのか？
本問では連立した式が4次方程式になってしまったため、図形的なアプローチで解いたが、実は、判別式のように数式的に解く方法も存在する。ただし、非常に計算が複雑になるため、解説で記載した解法をおすすめするが、高校数学の範囲で十分理解できる内容なので、数式的な解法が気になる人は【特別講義】共有点の一般的な求め方を確認されたい。

【徹底解説】共有点の個数を求める問題

【講義1】共有点と交点の違い

はじめに用語の確認から。本記事のタイトルにもなっている共有点と似た言葉に交点があります。

では、ここで質問です。共有点と交点の違いを説明できますか？

交点と共有点の違い

・交点　：直線や曲線が交わる点のこと。
・共有点：直線や曲線が、接したり交わったりする点のこと。

厳密な定義ではないですが、この理解で高校数学はOKです。つまり、共有点とは接点も含んだ交点というわけですね。確かに、交点というとお互いがクロスして突き抜けているイメージなので、例えば円と直線が接しているのを交点というのは変な気もしますね…（細かいですが）。

論証のときに交点と共有点の言葉の使い方で減点される可能性は低いと思いますが、中には細かい採点者もいるので、盤石にいくなら交点も接点も含んでいる共有点を使っておくのが無難でしょう。

【講義2】判別式で共有点の個数が求まるワケ

復習ですが、例えば2直線

\begin{cases}
\small y=x+1\\
\small y=-2x-3\\
\end{cases}

の交点の座標を求める場合、2つ方程式を連立して$\small x、y$の解を求めればよいのでした。

つまり、一般的に「共有点の座標を求める」＝「連立方程式を解く」ことになります。

円と直線の共有点を求める場合、その連立方程式は2次方程式になるので、「2次方程式の解の個数」＝「共有点の個数」となります。

2次方程式の解の個数は判別式からわかるので、円と直線の共有点の個数を求めるときには判別式が使われるわけです。

Point：判別式と共有点の個数

連立した式が2次方程式になる場合は、判別式で共有点の個数を求めることができる！

【講義3】判別式が使えない場合もある！？

円と直線のように連立した式が2次方程式になるので判別式で共有点の個数を求めることができることを解説してきました。

ということは、裏を返せば、連立した式が2次方程式ではない場合、判別式は使えないということです。意外とこの点に触れている参考書は少ないです。

たとえば、円と放物線の共有点を求めるために、連立方程式を解こうとすると、一般的には4次方程式になります。つまり、円と放物線の共有点の個数を求める場合は、判別式は使えないことになります。なので、円と放物線の位置関係から図形的に解いていく解法になるわけです（問題3参照）。

Point：判別式が使える問題

判別式で共有点の個数を求めることができるのは、連立した式が2次方程式の場合だけ。

【講義4】共有点の個数と解の配置問題

2次方程式でも線分と円の共有点や、直線と上半円（$\small x^2+y^2=1\space (y≧0)$のような上半分の円）の共有点など、$\small x$または$\small y$の範囲が制限されている場合は、判別式だけでは求まりません。このような場合は、解の配置問題を考える必要がでてきます（問題2参照）。

解の配置問題について、詳細は【解の配置問題】2次方程式の解の存在範囲の記事で解説しているので、ここではざっくりと説明すると、解の配置問題とは、ある条件を満たす解を持つ方程式を求める問題のことです。

たとえば、問題2のように、線分$\small \mathrm{AB}$と円の共有点を求める問題では、連立して得られた2次方程式 $\small 2x^2+4x-a^2+4=0$と条件$\small -3≦x≦2$が組み合わさることで、「2次方程式 $\small 2x^2+4x-a^2+4=0$が区間$\small -3≦x≦2$に解を持つための$\small a$の条件」を求める解の配置問題になります。

【特別講義】共有点の一般的な求め方

判別式を使って共有点を求めることができるのは、求める直線や曲線を連立した方程式が2次方程式の場合のみということを解説しました。

では、一般的に共有点の個数はどのように求めればよいのでしょうか？

一般的には、連立して得られた$\small n$次方程式の解の配置問題を考えることで共有点の個数を求めることができます。ただ、大学入試では出てこないので安心を。出てきても2次方程式以外は図形的なアプローチから攻めていきましょう。

ここでは問題3を例に、連立して得られる$\small x$の4次方程式を直接解く方法を参考として解説します。ただ、はじめに断っておくと、計算が非常に大変なので、解法としてはおすすめしません。なので、「今はテスト対策・受験対策で手がいっぱい…」という人は飛ばしてしまってOKです。

私がここであえて難解な解法を紹介する理由としては、

①図形的なアプローチ以外に数式的に解く方法もちゃんとあることを理解してもらうため
②複数の解法を理解することで解き方の選択肢が広がり数学力が鍛えられるため

です。紹介する論証は、流れ重視で細かい計算は端折っているので、自分で実際に計算しながら確認してみるとより理解が深まると思います。

　問題3 別解（数式的アプローチ）

求める方程式を連立して

$$\small x^4+(-2a+1)x^2+a^2-16=0$$

の4次方程式を得るところまでは一緒なので割愛。

$\small x^2=t$とおくと、考える方程式は $\small t^2+(-2a+1)t+a^2-16=0$となり2次方程式に帰着できる。

ここで、円の方程式 $\small x^2+(y-a)^2=16$より、共有点の存在範囲は円の定義域は$\small -4≦x≦4$に限られることから、$\small 0≦t≦16$。

よって、本問は、「2次方程式 $\small f(t)=t^2+(-2a+1)t+a^2-16=0$が区間 $\small 0≦t≦16$の範囲に実数解を何個持つか」という解の配置問題に置き換えることができる。

[1] $\small D<0$（実数解なし）の場合
\begin{split}
\small D &\small =(-2a+1)^2-4(a^2-16)<0\\
&\small \Leftrightarrow \space 4a^2-4a+1-4a^2+64<0\\
& \small \Leftrightarrow \space a>\frac{65}{4}\\
\end{split}
よって、$\small \displaystyle a>\frac{65}{4}$のとき共有点の個数は0個…①。

[2] $\small D=0$（重解）の場合
$\small D=0$から、$\small \displaystyle a=\frac{65}{4}$。このとき、$\small t$の実数解は、$\small t^2+(-2a+1)t+a^2-16=0$に代入すると
\begin{split}
&\small 16t^2-504t+3969=0\\
&\small \quad (4t-63)^2=0\\
&\small \qquad ∴\space t=\frac{63}{4}\\
\end{split}
となるため、
\begin{split}
\small x^2 &\small =\frac{63}{4}\\
\small x = &\small \pm \frac{3\sqrt{6}}{2}\\
\end{split}
この2解は、$\small -4≦x≦4$の範囲内なので、どちらも共有点となる。
よって、$\small \displaystyle a=\frac{65}{4}$のとき共有点の個数は2個…②。

[3] $\small D>0$（2つの異なる実数解あり）の場合
判別式の条件から、$\small \displaystyle a<\frac{65}{4}\space \cdots(*)$。

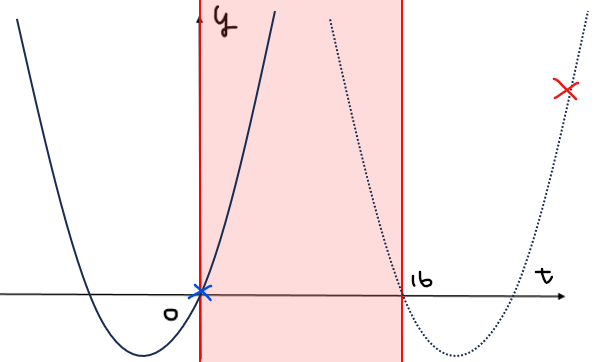
[3-1] $\small 0≦t≦16$の範囲に実数解を持たない場合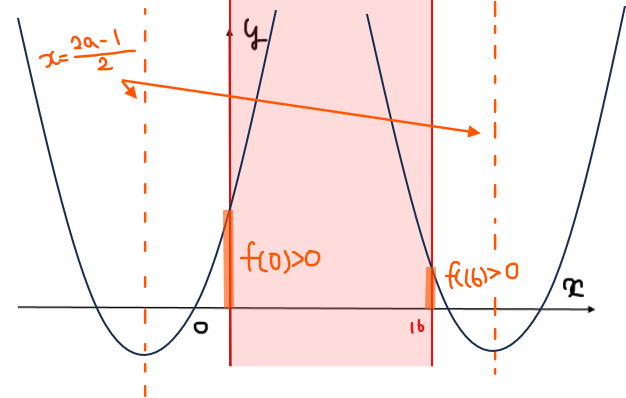

上図のような位置関係になるので、軸の範囲は
\begin{split}
\small & \small \frac{2a-1}{2}<0、\
\small & \small 16<\frac{2a-1}{2}\\
\small \Leftrightarrow \space & \small \color{red}{a<\frac{1}{2}、\frac{33}{2}<a}\\
\end{split}
境界条件は、
\begin{split}
\small &\small f(0)=a^2-16>0、\\
\small & \small f(16)=(a-16)^2>0\\
\small \Leftrightarrow \space & \small \color{blue}{a<-4、4<a<16、16<a}\\
\end{split}
よって、$\small (*)$と軸の範囲、境界条件の共通範囲から、$\small a<-4$のとき共有点の個数は0個…③。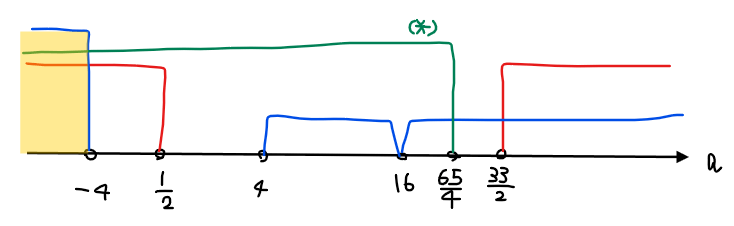

[3-2] $\small 0≦t≦16$の範囲に実数解を1つ持つ場合
大きく以下の2パターン。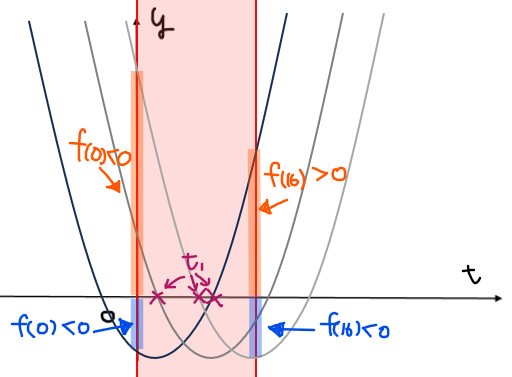

左上図のような位置関係のときは、軸には特に条件なし。
境界条件は、
\begin{split}
\small &\small f(0)f(16)=(a^2-16)(a-16)^2<0 \\
& \small \quad \Leftrightarrow \space -4<a<4\space (∵(a-16)^2≧0)\\
\end{split}
$\small -4<a<4$のとき、$\small 0<t<16$の範囲内の解は $\small t=t_1 \space \Leftrightarrow \space x=\pm\sqrt{t_1}$の2個より、共有点は2個…④。
一方、右上図のときは、軸の条件は
\begin{split}
&\small \frac{2a-1}{2}<0\\
& \quad \small a<\frac{1}{2}\\
\end{split}
境界条件は、$\small f(0)=a^2-16=0\space \Leftrightarrow \space a=\pm 4$。
よって、共通範囲を考えると、$\small a=-4$のとき、$\small t=0\space \Leftrightarrow \space x=0$のみであり共有点は1個…⑤。
※なお破線のパターンも可能性としてはあり得るが、軸と境界条件を同時に満たす$\small a$が存在しないため解説は割愛。

[3-3] $\small 0≦t≦16$の範囲に実数解を2つ持つ場合
条件を満たすパターンは下図の赤破線、黒実線、青破線の3パターン。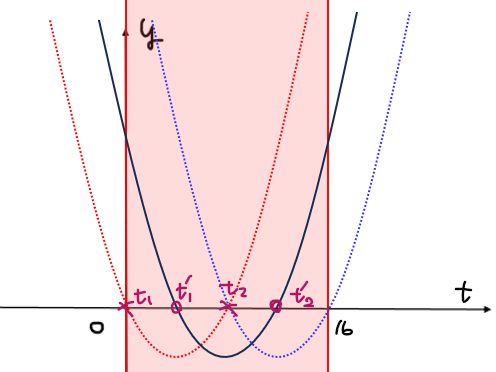

軸の条件はどのパターンでも共通で、$\small \displaystyle 0<\frac{2a-1}{2}<16 \space \Rightarrow \space \frac{1}{2}<a<\frac{33}{2}$。

赤破線のとき、境界条件 $\small f(16)=0\space \Rightarrow \space a=\pm4$より、軸との共通範囲は$\small a=4$。このとき、共有点の個数は、$\small t=0$で1個、$\small t=t_2$で2個なので、共有点は3個…⑥。

黒実践のとき、境界条件は、$\small f(0)>0、\mathrm{and} f(16)>0 \space \Rightarrow \space a^2-16>0、(a-16)^2>0 \space \Rightarrow \space a<-4、4<a<16、16<a$より、軸との共通範囲は、$\small \displaystyle 4<a<16、16<a<\frac{33}{2}$。さらに、判別式の条件$\small (*)$との共通範囲から、$\small \displaystyle 4<a<16、16<a<\frac{65}{4}$。共有点の個数は、$\small t=t_1’、t_2’$で実数解を持つので、$\small x$としては4つ実数解を持つことから、共有点の個数は4個…⑦。

青破線のとき、境界条件が$\small f(16)=(a-16)^2=0 \space \Rightarrow \space a=16$。これは軸の条件の範囲内なので、$\small a=16$のとき共有点は4個…⑧。

よって、①～⑧の合計範囲が答えになる。

≪参考≫
・共有点の個数が1個：①＋③
・共有点の個数が1個：⑤
・共有点の個数が2個：②＋④
・共有点の個数が3個：⑥
・共有点の個数が4個：⑦＋⑧（※）
　※$\small \displaystyle 4<a<16、16<a<\frac{65}{4}$と$\small a=16$が合体して、一つながりの範囲 $\small \displaystyle 4<a<\frac{65}{4}$になる