【関数の極限】不定形の全7パーンを分かりやすく解説（分数、ルート、三角関数などのn→∞、0の極限値）

今回は、関数の極限について、不定形と呼ばれる全7パターンの種類と求め方のコツを分かりやすく解説していきます。「分数型やルートの入ったの極限の求め方が分からない…」、「∞/∞や0/0といった不定形ってどうやって極限値を求めればいいの？」、「極限を求めるときのコツってあるの？」など関数の極限を求めるのが苦手な人でもわかるように基礎から解説するので、ぜひ最後まで読んでみてください！

• 分数やルートが含まれる多項式関数の極限値の求め方が知りたい
• ∞/∞や0/0、∞×0などのいわゆる「不定形」って何？全部で何パターンあるの？
• 問題ごとに式変形の仕方がたくさんあるけど、結局どう解けばいいの？

【はじめに】不定形とはなにか？

極限を求める問題の中で少し厄介なのが「不定形」の極限を求める問題です。
不定形とは、∞/∞や0/0のような形になる極限のことで（後ほど個別に解説）、ちゃんと計算しないと値が定まらないことから「不定形」と呼ばれています。

言葉だけだとわからないと思うので、具体例で説明します。
たとえば
$$
\begin{equation}
\begin{split}
&\lim_{x \to \infty} \frac{x}{2x}\\
&\lim_{x \to \infty} \frac{3x}{x}\\
\end{split}
\end{equation}
$$
の極限は、そのまま単純に\(\small x\to\infty\)としてしまうと、どちらも∞/∞となってしまいますが、ちゃんと計算してから極限をとれば
$$
\begin{equation}
\begin{split}
&\lim_{x \to \infty} \frac{x}{2x}=\color{red}{\frac{1}{2}}\\
&\lim_{x \to \infty} \frac{3x}{x}=\color{red}3\\
\end{split}
\end{equation}
$$
のように極限値を求めることができます。
ここでポイントになるのが、最初はどちらも∞/∞だったのに計算してみると値が異なっているという点です。このように、∞/∞という形だけでは値が定まらないので「不定形」と呼ばれるわけです。

関数の極限を求める手順

関数の極限の問題を解く手順を整理しておきましょう。関数の極限を求めるときには、だいたいは以下の手順で考えていけば大丈夫です。

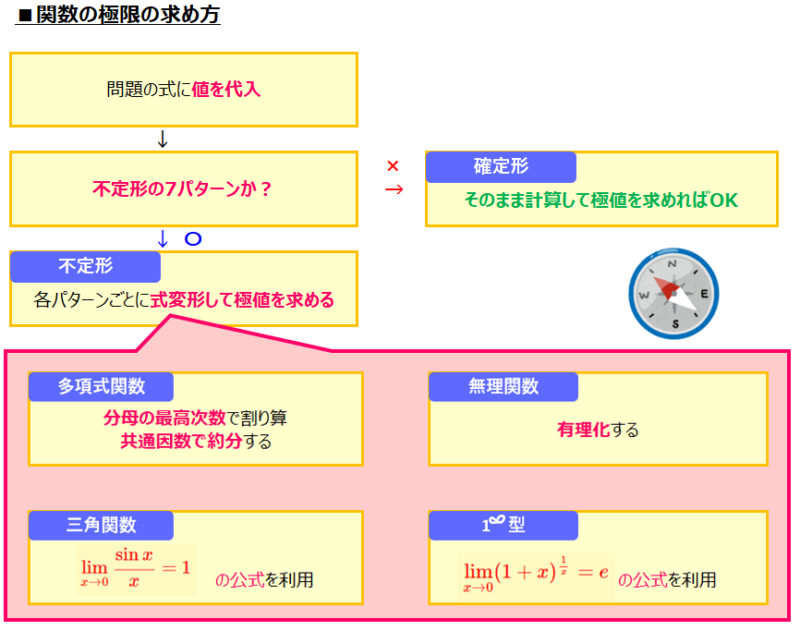
まずは問題の式で極限をとってみて値が求まるのか、不定形になるのかを確認します。不定形かどうかの判断は、この後説明する不定形の7パターンに当てはまるかどうかで判断できます。不定形でなければ、値が確定するのでその値が極限、不定形であれば式変形して極限を求めるというのが大まかな流れです。

では、具体的に不定形の7パターンとパターンごとの解き方について学んでいきましょう！

【極限の不定形】全7パターンを解説

【パターン別】不定形の極限の求め方

↓↓各問題の解説はこちら

• 問題(1)の解説
• 問題(2)の解説
• 問題(3)の解説
• 問題(4)の解説
• 問題(5)の解説
• 問題(6)の解説
• 問題(7)の解説

不定形はどんな問題でも上記7パターンのどれかに当てはまるので、しっかり覚えておきましょう！
また、式変形の方法はパターンごとというよりは、関数ごとに方針が異なるのでこの後の問題で一緒に確認していきましょう。
では、具体的な解法をそれぞれ確認していきます。

パターン①：∞/∞型

そのまま、\(\small x \to \infty\)とすると、\(\small \displaystyle \color{blue}{\frac{\infty}{\infty}}\)となり、∞/∞型の不定形となります。
このような場合は、収束する形に式変形します。収束する形がどんな形かは問題によるため、ある程度の慣れが必要です。ただ、それほどパターンは多くないので後で類題を載せておきます。
今回は多項式関数なので、分母の最高次数の文字で分母・分子を割り算することで発散を回避します。

$$
\begin{equation}
\begin{split}
\lim\limits_{x \to \infty} &\frac{3x^2-x+2}{x^2-2x+1}\\
=\lim\limits_{x \to \infty} &\frac{3-\frac{1}{x}+\frac{2}{x^2}}{1-\frac{2}{x}+\frac{1}{x^2}}\\
=&\frac{3-\color{red}0+\color{red}0}{1-\color{red}0+\color{red}0}\\
=& \space \color{red}{3 \quad \cdots (答)}\\
\end{split}
\end{equation}
$$

(1) 分母の中で一番発散スピードが速い(すぐに無限大になる)項は\(\small 4^x\)なので、分母・分子を\(\small 4^x\)で割ると
$$
\begin{equation}
\begin{split}
\lim\limits_{x\to\infty} \frac{3^x}{2^x+4^x} &=\lim\limits_{x\to\infty} \frac{\left(\frac{3}{4}\right)^x}{\left(\frac{2}{4}\right)^x+1}\\
&=\frac{\color{red}0}{\color{red}0+1}\\
&= \color{red}{0\quad\cdots(答)}\\
\end{split}
\end{equation}
$$

(2) 分母・分子を\(\small x\)で割ると
$$
\begin{equation}
\begin{split}
\lim\limits_{x\to\infty} \frac{2x^3-2x+1}{x+3} &=\lim\limits_{x\to\infty} \frac{2x^2-2+\frac{1}{x}}{1+\frac{3}{x}}\\
&=\frac{\color{red}\infty -2+\color{red}0}{1+\color{red}0}\\
&= \color{red}{\infty \quad\cdots(答)}\\
\end{split}
\end{equation}
$$

パターン②：0/0型

問題の式で\(\small x \to 2\)をそのまま計算すると
$$
\begin{equation}
\begin{split}
\lim\limits_{x \to 2} &\frac{x^3-3x-2}{x^2-x-2}\\
=&\frac{8-6-2}{4-2-2}\\
=&\space \color{blue}{\frac{0}{0}}\\
\end{split}
\end{equation}
$$
となり0/0型の不定形です。0/0型の極限も問題によって解き方が何パターンかあるので、類題で紹介します。今回は多項式関数なので、因数分解してゼロになる部分を約分で取り除きましょう。
$$
\begin{equation}
\begin{split}
\lim\limits_{x \to 2} &\frac{x^3-3x-2}{x^2-x-2}\\
=\lim\limits_{x \to 2} &\frac{(x-2)(x^2+2x+1)}{(x+1)(x-2)}\\
=\lim\limits_{x \to 2} &\frac{x^2+2x+1}{x+1}\\
=&\space \frac{9}{3}\\
=&\space \space \color{red}{3 \quad \cdots (答)}\\
\end{split}
\end{equation}
$$

(1)無理関数の極限で、\(\small x\to1\)で0/0になる不定形です。ルートがある場合は、有理化すると分母が0になることを回避できるので、分母・分子に\(\small \sqrt{x+3}+2\)を掛け算することで
$$
\begin{equation}
\begin{split}
&\lim\limits_{x\to 1} \frac{(\sqrt{x+3}-2)\color{red}{\cdot(\sqrt{x+3}+2)}}{(x^2-1)\color{red}{\cdot(\sqrt{x+3}+2)}}\\
=&\lim\limits_{x\to 1} \frac{(x+3)-4}{(x+1)(x-1)(\sqrt{x+3}+2)}\\
=&\lim\limits_{x\to 1} \frac{\color{blue}{x-1}}{(x+1)\color{blue}{(x-1)}(\sqrt{x+3}+2)}\\
=&\lim\limits_{x\to 1} \frac{1}{(x+1)(\sqrt{x+3}+2)}\\
=&\frac{1}{(\color{red}1+1)(\sqrt{\color{red}1+3}+2)}\\
=&\frac{1}{2\cdot4}\\
&=\color{red}{\frac{1}{8} \quad \cdots (答)}
\end{split}
\end{equation}
$$

(2)三角関数の極限の問題では、0/0型のパターンに限らず
$$\lim_{x\to0} \frac{\sin x}{x}=1$$
の公式を使うことを意識して式変形するとよいです。今回の問題では、分母に\(\small 1-\cos x\)があるので、無理やり\(\small \sin x\)を作り出すために、2倍角の公式
$$
\begin{equation}
\begin{split}
&\cos2x=1-2\sin^2 x\\
\end{split}
\end{equation}
$$
で、\(\small 2x\)を\(\small x\)に置き換えることで
$$
\begin{equation}
\begin{split}
&\cos x=1-2\sin^2 \left(\frac{x}{2}\right)\\
&\color{red}{1-\cos x=2\sin^2 \left(\frac{x}{2}\right)}\\
\end{split}
\end{equation}
$$
この関係式を使うことで、
$$
\begin{equation}
\begin{split}
&\lim\limits_{x\to 0} \frac{x^2}{\color{red}{1-\cos x}}=\lim\limits_{x\to 0} \frac{x^2}{\color{red}{2\sin^2 \left(\frac{x}{2}\right)}}\\
&\\
\end{split}
\end{equation}
$$
\(\small \displaystyle t=\frac{x}{2}\)とおくと、\(\small x=2t\)なので、\(\small x\to0\)で\(\small t\to0\)となることから、
$$
\begin{equation}
\begin{split}
\lim\limits_{x\to 0} \frac{x^2}{2\sin^2 \left(\frac{x}{2}\right)}&=\lim\limits_{t\to 0} \frac{(2t)^2}{2\sin^2 t}\\
&=\lim\limits_{t\to 0} \frac{2t^2}{\sin^2 t}\\
&=2 \lim\limits_{t\to 0} \left(\frac{t}{\sin t}\right)^2\\
&=2 \lim\limits_{t\to 0} \dfrac{1}{\left(\color{red}{\frac{\sin t}{t}}\right)^2}\\
&=2\cdot\frac{1}{\color{red}1}\\
&=\color{red}{ 2\quad\cdots(答)}
\end{split}
\end{equation}
$$

パターン③：∞-∞型

有理化すると、
$$
\begin{equation}
\begin{split}
&\lim\limits_{x \to \infty} (\sqrt{x^2+3x+4}-x)\\
=&\lim\limits_{x \to \infty} \frac{(\sqrt{x^2+3x+4}-x)\color{red}{(\sqrt{x^2+3x+4}+x)}}{\color{red}{\sqrt{x^2+3x+4}+x}}\\
=&\lim\limits_{x \to \infty} \frac{(x^2+3x+4)-x^2}{\sqrt{x^2+3x+4}+x}\\
=&\lim\limits_{x \to \infty} \frac{3x+4}{\sqrt{\color{red}{x^2+3x+4}}+x}\\
\end{split}
\end{equation}
$$
この式で\(\small n\to\infty\)とすると、∞/∞型のパターンになっているので、分母の最高次数\(\small x\)をくくりだすと(最高次数は\(\small x^2\)のように見えるが、ルートの中にあるので\(\small x\)が最高次数)、
$$
\begin{equation}
\begin{split}
(与式)=&\lim\limits_{x \to \infty} \frac{3x+4}{\sqrt{\color{red}{x^2(1+\frac{3}{x}+\frac{4}{x^2})}}+x}\\
=&\lim\limits_{x \to \infty} \frac{3x+4}{\color{red}{x}\sqrt{\color{red}{1+\frac{3}{x}+\frac{4}{x^2}}}+x}\\
=&\lim\limits_{x \to \infty} \frac{\color{blue}x\left(3+\frac{4}{x}\right)}{\color{blue}x\left(\sqrt{1+\frac{3}{x}+\frac{4}{x^2}}+1\right)}\\
=&\lim\limits_{x \to \infty} \frac{3+\frac{4}{x}}{\sqrt{1+\frac{3}{x}+\frac{4}{x^2}}+1}\\
=&\frac{3+\color{red}0}{\sqrt{1+\color{red}0+\color{red}0}+1}\\
=&\color{red}{\space \frac{3}{2} \quad \cdots (答)}
\end{split}
\end{equation}
$$

$$
\begin{equation}
\begin{split}
&\lim\limits_{x\to \infty} (\sqrt{x+1}-\sqrt{x})\\
=&\lim\limits_{x\to \infty} \frac{(\sqrt{x+1}-\sqrt{x})\color{red}{(\sqrt{x+1}+\sqrt{x})}}{\color{red}{\sqrt{x+1}+\sqrt{x}}}\\
=& \lim\limits_{x\to \infty} \frac{(x+1)-x}{\color{red}{\sqrt{x+1}+\sqrt{x}}}\\
=& \lim\limits_{x\to \infty} \frac{1}{\sqrt{x+1}+\sqrt{x}}\\
=& \space \color{red}{0 \quad \cdots (答)}\\
\end{split}
\end{equation}
$$
最後の式変形は、1/∞なので0になります。このように、ほとんどの場合、有理化したあとは「∞/∞型」になるか、「定数/∞→０」になります。

パターン④：∞×0型

問題の式でそのまま\(\small x\to\infty\)をとると
$$
\begin{equation}
\begin{split}
\lim\limits_{x \to \infty} x \sin \frac{1}{x}&=\color{red} \infty \times \sin \color{red}{\frac{1}{\infty}}\\
&=\infty \times \sin 0\\
&=\color{blue}{\infty \times 0}\\
\end{split}
\end{equation}
$$
となり、∞×0型の不定形です。

今回は、sinが入っているので、
$$\lim_{x\to0} \frac{\sin x}{x}=1$$
を使うことを意識して式変形します。問題の式を見るとsinの中身が\(\small \displaystyle \frac{1}{x}\)となっているので、\(\small \displaystyle t=\frac{1}{x}\)とおくと、
$$
\begin{equation}
\begin{split}
\lim\limits_{x \to \infty}x\sin \frac{1}{x}&=\lim\limits_{\color{red}t \to \infty}\color{red}{\frac{1}{t} \sin t}\\
&=\lim\limits_{t \to \infty}\frac{\sin t}{t}\\
&=\color{red}{1 \quad \cdots(答)}\\
\end{split}
\end{equation}
$$

パターン⑤：\(\small 1^\infty\)型

問題の式で、そのまま\(\small x\to\infty\)とすると\(\small 1^\infty\)となることが分かります。このような場合は、ポイントにも記載の通り、自然対数の定義の形に持ち込んで極限を求めていきます。

\(\small t=2x\)とおくと、\(\small \displaystyle x=\frac{t}{2}\)なので、\(\small x\to0\)で\(\small t\to0\)となる。\(\small t\)を使って問題の式を書き換えると
$$
\begin{equation}
\begin{split}
\lim\limits_{x \to 0} \left( 1+2x \right)^{\frac{1}{4x}} &= \lim\limits_{\color{red}t \to 0} \left( 1+\color{red}t \right)^{\frac{1}{\color{red}{2t}}} \\
&=\left[ \space \color{blue}{\lim\limits_{t \to 0} \left( 1+t \right)^{\frac{1}{t}} }\right]^{\frac{1}{2}}\\
&=\color{red}{\sqrt{e}\quad\cdots(答)}
\end{split}
\end{equation}
$$

パターン⑥：\(\small 0^0\)型

不定形のパターンとして載せていますが、ほとんど見かけることはないです。

問題の式で\(\small x\to\infty\)とすると
$$\lim\limits_{x \to \infty} \left( e^{-{x^2}}\right)^{\frac{1}{x^2}}=(e^{-\color{red}{\infty}})^{\color{red}{\frac{1}{\infty}}}=\color{blue}{0^0}$$
となりますが、明らかに指数部分が約分できるので、計算してから極限をとると
$$\lim\limits_{x \to \infty} \left( e^{-{x^2}}\right)^{\frac{1}{x^2}}=\lim\limits_{x \to \infty} e^{-1}=\color{red}{\frac{1}{e}\quad\cdots(答)}$$

パターン⑦：\(\small \infty^0\)型

誘導なしだとかなり難問になっているので、(1)、(2)と誘導を付けています。

(3)が\(\small \infty^0\)型の不定形になっています。こちらもほとんど見ることはないパターンですが、紹介しておきます。ちなみに、(1)は不定形ではないシンプルな極限の問題、(2)は∞/∞型の不定形です。

(1)\(\small \displaystyle \color{blue}{\frac{2}{e}<1}\)より、
$$\lim\limits_{x \to \infty} \left(\frac{2}{e}\right)^x=\color{red}{0 \quad \cdots (答)}$$

(2)\(\small \color{blue}{x<2^x}\)より
$$
\begin{equation}
\begin{split}
x &<2^x \\
\frac{x}{e^x} &<\frac{2^x}{e^x}
\end{split}
\end{equation}
$$
両辺で\(\small x\to\infty\)の極限をとると
$$
\begin{equation}
\begin{split}
\lim_{x\to\infty} \frac{x}{e^x}≦ \lim_{x\to\infty} \frac{2^x}{e^x}
\end{split}
\end{equation}
$$
右辺は(1)の結果から0であり、\(\small \displaystyle \frac{x}{e^x}\)についても、\(\small x\to\infty\)では\(\small \displaystyle 0≦\frac{x}{e^x}\)なので、
$$
\begin{equation}
\begin{split}
&0≦\lim_{x\to\infty} \frac{x}{e^x}≦ \lim_{x\to\infty} \frac{2^x}{e^x}\\
&0≦\lim_{x\to\infty} \frac{x}{e^x}≦ 0.\\
\end{split}
\end{equation}
$$
よって、はさみうちの原理から
$$\lim_{x\to\infty} \frac{x}{e^x}=0$$
よって、題意は示された 。

補足：\(\small x＜０\)の場合、\(\small \displaystyle 0≦\frac{x}{e^x}\)は成り立たないのに、なぜ0以上としていいの？
たとえば、\(\small x=-1\)の場合、
$$\left. \frac{x}{e^x} \right|_{x=-1}=\frac{-1}{e^{-1}}=-e<0$$
となり、確かに\(\small \displaystyle \frac{x}{e^x}<0\)になります。ただ、今回考えている極限は\(\small x\to\infty\)というプラスのとてつもなくデカい数であり、\(\small x\)がマイナスになることはないので\(\small \displaystyle 0≦\frac{x}{e^x}\)と考えてよいというわけです。

(3)問題の式で\(\small x\to\infty\)とすると
$$\lim\limits_{x \to \infty} x^{\frac{1}{x}}=\color{red}\infty^{\frac{1}{\color{red}\infty}}=\color{blue}{\infty^0}$$
となり、\(\small \infty^0\)型の不定形です。今回は、指数部分の\(\small x\)をうまく処理するため、\(\small y=x^\frac{1}{x}\)とおいて両辺の対数をとった極限を考えるとうまくいきます。つまり、求めたい極限は
$$\lim_{x\to\infty} x^{\frac{1}{x}}= \lim_{x\to\infty}y \quad \cdots①$$
です。

\(\small \displaystyle y=x^\frac{1}{x}\)の両辺の対数をとると
$$
\begin{equation}
\begin{split}
\log \color{red}y&= \log \color{red}{x^{\frac{1}{x}}}\\
\log y&= \frac{1}{x}\log x\\
\color{blue}{\lim_{x\to\infty}} \log y&= \color{blue}{\lim_{x\to\infty}} \frac{\log x}{x}\quad \cdots②\\
\end{split}
\end{equation}
$$

右辺について、\(\small t=\log x\)とおくと、\(\small x=e^t\)より、\(\small x\to\infty\)で\(\small t\to\infty\)なので
$$\lim_{x\to\infty} \frac{\log x}{x}=\color{red}{\lim_{t\to\infty} \frac{t}{e^t}=0}.$$
ただし、赤字箇所は(2)の結果を用いています。

この結果を②の式に代入すると
$$
\begin{equation}
\begin{split}
\lim_{x\to\infty} \log y&= \lim_{x\to\infty} \frac{\log x}{x}=0\\
\end{split}
\end{equation}
$$
\(\small x\to\infty\)で\(\small \log y\)の極限が0であることが分かったので、logの中身である\(\small y\)自身の極限値は
$$\lim_{x\to\infty} y=1$$

よって、①の関係式から
$$\lim_{x\to\infty} x^{\frac{1}{x}}=\color{red}{1 \quad \cdots (答)}$$

【補足】7パターン以外の極限は不定形ではなく確定形！

関数の極限をとったときに、不定形の7パターン以外となった場合はすべて「確定形」になります。たとえば、\(\small \displaystyle \frac{1}{\infty}=0\)（分子が定数で分母が無限大なので）、\(\small \displaystyle \frac{1}{+0}=\infty\)（「+0」はプラス方向から0に近づけることを意味する）、\(\small 0^\infty=0\)のように、∞が含まれていたとしても不定形以外のパターンであれば式変形せずに答えが決まるので、注意しましょう。

【まとめ】関数の極限の解き方

今回は、関数の極限の求め方について不定形とは何か、どんなパターンがあるのかとパターンごとの解き方を説明しました。

内容を簡単に整理すると以下の通りです。

今回解説した不定形の極限の問題以外にも、極限の収束条件（極限×三角関数）などの問題も解説しているので、興味がある人はぜひ読んでみてください！

では、本日はここまでです。お疲れさまでした！