本記事では、ベクトル方程式の中でも苦手な人が多い「終点の存在範囲」について解説します。「関係式がたくさん出てくるけど、なにをどこまで覚えたらいいの?」、「関係式が表す意味って結局どういうこと?」、「終点の存在範囲はどうやって図示すればいいの?」といった疑問を抱えている人向けに、絶対に覚えておきたい問題のパターン3選とそれぞれを活用した具体的な問題の解き方についてわかりやすく解説しているので、ぜひ最後まで読んでみてください!
- 終点の存在範囲がどういう意味かが分からない
- 終点の存在範囲を表す関係式の図形的な意味が分からない
- 終点の存在範囲の求め方/図示の仕方が分からない
【導入編】終点の存在範囲とは
そもそも、本記事のタイトルにもなっている「終点の存在範囲」がどういう意味なのかをまず初めに説明します。
終点の存在範囲とは、「2つのベクトルを足し算した答え全部」のこと。
上記は正確な定義ではありませんが、ここではイメージだけつかめればokです。
終点の存在範囲の問題では、「\(\small \vec{p}=s\vec{a}+t\vec{b},s+t=1\)」といった式がよく登場します。文字がたくさんあって難しそうに見えますが、シンプルに言語化すれば、「\(\small \vec{a}\)と\(\small \vec{b}\)を足し算したベクトル\(\small \vec{p}\)を求めよ」といわれているだけです。
そして、足し算した答えである\(\small \vec{p}\)は、\(\small \vec{a}\)と\(\small \vec{b}\)の係数である\(\small s,t\)の値によって当然答えが変わるので、答えになり得るすべてのパターンを解答しようとすると、結果として、直線や線分といった「図形」になるので、これらを「存在範囲」といっているだけです。

【解説編】終点の存在範囲の基本パターン3選
終点の存在範囲の意味が理解できたところで、早速、本題である終点の存在範囲の求め方について解説します。いくつかパターンがあるのですが、今回は思い切ってよくでる基本の3パターンに厳選して紹介していこうと思います!
\(\small \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)を考える。
このとき、終点Pの存在範囲は、実数\(\small s,t\)の条件によって決まる。
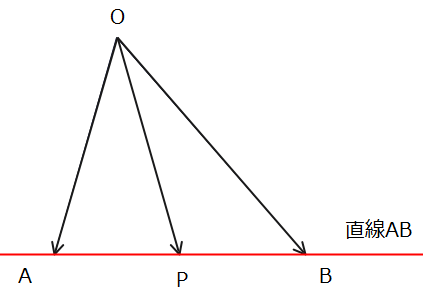
- 【基本パターン1】終点の存在範囲が直線上になるパターン
→条件:\(\small s+t=1\)
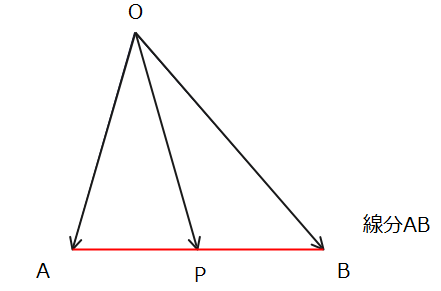
- 【基本パターン2】終点の存在範囲が線分になるパターン
→条件:\(\small s+t=1\)かつ\(\small s≧0、t≧0\)
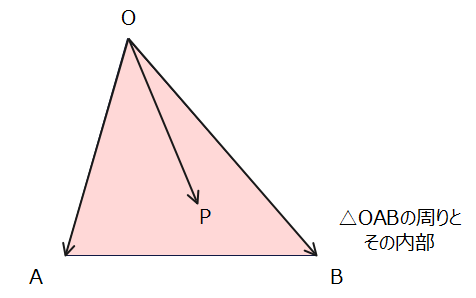
- 【基本パターン3】終点の存在範囲が三角形OABの周りとその内部になるパターン
→条件:\(\small s+t≦1\)かつ\(\small s≧0、t≧0\)
3パターンだけでも条件がいろいろあって覚えようとすると大変ですよね?なので、ここからはそれぞれのパターンごとに、「その条件だとなぜその存在範囲になるのか?」を詳しく解説するので、理由の部分をしっかり理解しましょう!
2.1 【基本パターン1】存在範囲が直線上になる条件の意味
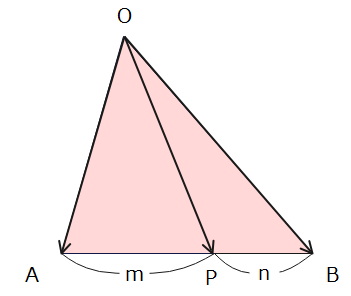
これは、三角形OABに対して辺ABをm:nに内分または外分する点の集合です。
- 三角形OABの辺ABをm:nに内分する点Pは

$$\overrightarrow{OP}=\frac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}$$ - 三角形OABの辺ABをm:nに外分する点Pは

$$\overrightarrow{OP}=\frac{-n\overrightarrow{OA}+m\overrightarrow{OB}}{m-n}$$
内分点の公式では、\(\small \overrightarrow{OA}\)の係数である\(\frac{n}{m+n}=s\)、\(\small \overrightarrow{OB}\)の係数である\(\small \frac{m}{m+n}=t\)とおけば、s+t=1で\(\small \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)となります。外分点についても同様の方法でsとtを設定することで同じ結果になります。
よって、係数同士を足してちょうど1になるときは、終点Pは辺ABの内分点または外分点なので、つまりは直線AB上のどこかにあるということになります。
もっと具体的に理解したいひとは、例えば、「三角形OABにおいて辺ABを1:2に内分する点をPとするとき\(\small \overrightarrow{OP}\)を\(\small \overrightarrow{OA}\)と\(\small \overrightarrow{OB}\)で表せ」という問題を考えるとよいでしょう。答えは、内分点の公式より\(\small \overrightarrow{OP}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}\)となるので、確かに係数を足すと\(\small \frac{2}{3}+\frac{1}{3}=1\)となっていることが分かります。
2.2 【基本パターン2】存在範囲が線分ABになる条件の意味
先程の直線ABになるパターンの条件に「s≧0、t≧0」が追加されると存在範囲が線分ABに限定されます。念のため、直線ABと線分ABの違いは、直線ABは2点A、Bを通り無限に伸びる線なのに対して、線分ABは、点Aと点Bを結ぶ線(つまり辺AB)だという点です。用語の意味が曖昧だと最初のパターンと何が違うのかわからなくなってしまうので、注意が必要です。
条件に「s≧0、t≧0」が追加されるとなぜ、直線から線分に存在範囲が限定されるのでしょうか。答えはこれまた内分点と外分点の公式にあります。
例えば、「三角形OABにて辺ABを3:2に外分する点をPとするとき\(\small \overrightarrow{OP}\)を\(\small \overrightarrow{OA}\)と\(\small \overrightarrow{OB}\)で表せ」という問題を考えてみましょう。答えは、\(\small \overrightarrow{OP}=-2\overrightarrow{OA}+3\overrightarrow{OB}\)となります。もちろん、s=-2、t=3とおけば、s+t=1は満たしています。しかし\(\small \overrightarrow{OA}\)の係数が-2と負の値になっています。
実は、外分点の公式では、必ずsかtのどちらかが負の値になります。もっとシンプルに言えば、必ずどちらかの係数がマイナスになるということです。これは簡単に証明できるので皆さんもぜひ考えてみてください(本記事の最後にを載せておきます)。
逆に、内分点の公式では、どちらの係数も必ずプラスになります。つまり、終点Pが線分AB上にある(=辺ABを内分する)場合は、係数に「s≧0、t≧0」という条件が追加されるということです。
2.3 【基本パターン3】存在範囲が三角形OABの周りとその内部になる条件の意味
最後は、線分ABの条件で「s≧0、t≧0 かつ s+t=1」の部分が「s≧0、t≧0 かつ s+t≦1」と条件が緩められると、なぜ三角形の内部まで存在範囲が広がるのかについて説明します。
存在範囲が線分ABの時は、係数同士を足したらぴったり1にならないといけなかったのに対して、今回は1以下なので、\(\frac{1}{2}\)でも\(\frac{2}{3}\)でもokということで、条件が緩められています。
では、具体的に係数同士の和が\(\frac{1}{2}\)になる場合で終点Pがどんな位置にいるのかを考えてみましょう。
実数\(\small s,t\)が、条件\(\small s≧0、t≧0\)と\(\small s+t=\frac{1}{2}\)を満たすとき、\(\small \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)で表される終点Pの位置を図示せよ。
これは、先程紹介した線分AB上に存在するパターンに帰着させて解くことが可能です。
条件式\(\small s+t=\frac{1}{2}\)の両辺を2倍すると\(\small 2s+2t=1\)となるので、\(\small m=2s、n=2t\)とおき直すと、条件式と問題は
$$m≧0、n≧0、m+n=1のとき、\overrightarrow{OP}=\frac{m}{2}\overrightarrow{OA}+\frac{n}{2}\overrightarrow{OB}となる点\mathrm{P}を図示せよ。$$
という問題に置き換えることができます。ただし、ベクトルの和の部分では、\(\small m=2s、n=2t\)とおいたので、\(\small s=\frac{m}{2}、t=\frac{n}{2}\)の関係を代入してます。
そうすると、条件については線分ABの時と同じです。異なるのはベクトルの和の式の係数が2で割られた状態になっていること。これは、
$$\overrightarrow{OP}=m\left( \frac{\overrightarrow{OA}}{2}\right)+n \left(\frac{\overrightarrow{OB}}{2}\right)$$
というひとまとまりで考えると、\(\small \overrightarrow{OA}\)を半分にしたベクトルと\(\small \overrightarrow{OB}\)を半分にしたベクトルで構成される三角形の線分上…(答)ということになります。
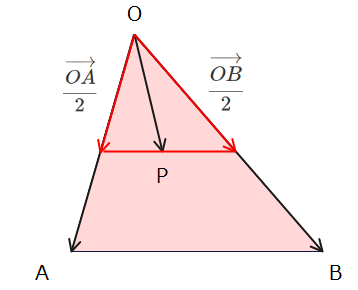
このように、係数の和が\(\frac{1}{2}\)以外の場合でも同様の方法で点Pの存在範囲は辺OAと辺OB上のどこかの点を結んだ線分上になるため、結果として、係数の和が1以下の場合は、三角形の内部とその周りが存在範囲となります。係数の和=0の時は点O、係数の和=1の時は辺AB、係数の和が0~1の時はその間のどこかという感じです。
ちなみに、「その周り」というのは三角形OABの周辺のことで、s=0の場合が辺OB上、t=0の場合が辺OA上、s>0,t>0かつs+t=1の時が辺AB上になります。
2.4 応用問題は基本の3パターンに当てはめて解く
終点の存在範囲の問題のほとんどは、今回紹介した基本の3パターンに当てはめて解くことができます。なのでそのままでは3パターンのどれかには当てはまらなくても文字の置き換えなどをして当てはめることができないかをまず考えるのがよいでしょう。
また、今回紹介した基本の3パターンに当てはまらない場合もあるので、そのような問題に対処するためには、基本の3パターンの考え方を理解するのが重要です。3パターンをただ単に暗記してしまうと、このパターン以外の条件が出てきたときにお手上げになってしまいますが、しっかり考え方を理解できていれば、この3つ以外の条件が出てきたときでも、考え方を応用して解くことができます。
では、どのくらい考え方が理解できたか、理解した考え方を使ってどう問題を解くのかを演習編で確認していきましょう!
【演習編】終点の存在範囲を求めてみよう
3.1【問題1(基本)】係数の和が1にならない場合の対処
三角形OABにおいて、\(\small s,t\)を実数とし、\(\small \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)を考える。このとき、\(\small 4s+3t=2\)の場合の終点Pの存在範囲を図示せよ。
係数の和の条件のみなので、解説編の基本パターン1の形に持っていきます。
「係数の和=1」の形を作るため、\(\small 4s+3t=2\)の両辺を2で割ると、\(\small 2s+\frac{3}{2}t=1\)。\(\small u=2s,v=\frac{3}{2}t\)とおくと、条件は、\(\small u+v=1(u,vは実数)\)となります。
条件式を\(\small u,v\)のみで表せたので、次は\(\small \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)の式も\(\small u,v\)を使って表しましょう。
$$
\begin{equation}
\begin{split}
& \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\\
& \overrightarrow{OP}=\frac{u}{2}\overrightarrow{OA}+\frac{2}{3}v \overrightarrow{OB}\\
& \overrightarrow{OP}=u\left( \frac{1}{2}\overrightarrow{OA}\right)+v\left( \frac{2}{3}\overrightarrow{OB}\right)\\
\end{split}
\end{equation}
$$
ここで、\(\small \frac{1}{2} \overrightarrow{OA}=\overrightarrow{OA’}\)、\(\small \frac{2}{3} \overrightarrow{OB}=\overrightarrow{OB’}\)とおくと、上式は、\(\small \overrightarrow{OP}=u\overrightarrow{OA’}+v\overrightarrow{OB’}\)となり、条件式、\(\small u+v=1(u,vは実数)\)と合わせて解説編の基本パターン1の形になりました。
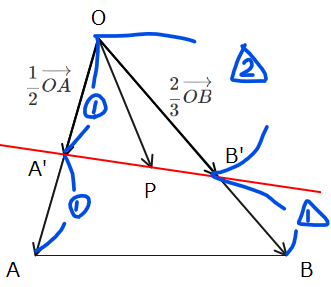
よって、答えは直線A’B’上が点Pの存在範囲になりますが、点A’、B’は解答する中でこちらが決めた点なので、回答を見る人が分かるように言語化しておきましょう。
点B’の位置が分かりにくいですが、\(\small \overrightarrow{OB’}=\frac{2}{3}\overrightarrow{OB}\)ということは、「点Oと点B’を結んだベクトルは、点Oと点Bを結んだベクトルを3個に分けたうちの2つ分(\(\small =\frac{2}{3}\)倍)」ということなので、端的に言えば「線分OBを2:1に内分した点」となります。
線分OAの中点をA’、線分OBを2:1に内分する点をB’とおいたとき、点Pの存在範囲は直線A’B’…(答)。
3.2【問題2(基本)】係数の和が不等式になっている場合の対処
三角形OABにおいて、\(\small s≧0,t≧0\)(s,tは実数)とし、\(\small \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)を考える。このとき、\(\small 2< s+t <3\)の場合の終点Pの存在範囲を図示せよ。
\(\small s+t\)が一定値ではなく不等式になっていることから、解説編の基本パターン3の形に持っていく。
「係数の和≦1」の形にするべく、条件式の全体を3で割ると
$$\small \displaystyle \frac{2}{3}<\frac{s}{3}+\frac{t}{3}<1$$
ここで、\(\small \displaystyle \frac{s}{3}=u、\frac{v}{3}=v\)とおくと、
$$\small \displaystyle \frac{2}{3}<u+v<1$$
また、\(\small s=3u、t=3v\)より
\begin{split}
\small \overrightarrow{OP}&\small =s\overrightarrow{OA}+t\overrightarrow{OB}\\
&\small = 3u\overrightarrow{OA}+3v\overrightarrow{OB}\\
&\small = u(3\overrightarrow{OA})+v(3\overrightarrow{OB})\\
\end{split}
ここで、\(\small 3\overrightarrow{OA}=\overrightarrow{OA’}、3\overrightarrow{OB}=\overrightarrow{OB’} \space \cdots ①\)とおくと、上式は
\begin{split}
\small \overrightarrow{OP}&\small = u\overrightarrow{OA’}+v\overrightarrow{OB’} \quad (\frac{2}{3}<u+v<1)\\
\end{split}
上式は、基本パターン3と非常に似ているが係数の和の範囲に下限がある点に注意する。「係数の和≦1」の場合は、終点の存在範囲は三角形内部だったが、下限がついているということは、三角形の内部の一部は範囲外になるということがイメージできる。
では、ある程度終点の存在範囲のイメージを沸かせたところで、実際に図を書きながら範囲を求めていこう。まず、条件式が\(\small \overrightarrow{OP} = u\overrightarrow{O\color{red}{A’}}+v\overrightarrow{O\color{red}{B’}} \)であることから、\(\small \mathrm{△OA’B’}\)を図示する。
点\(\small \mathrm{A’、B’}\)がどんな点だったかを忘れてしまった人は①を思い出すと、線分\(\small \mathrm{OA、OB}\)をそれぞれ3倍に延長した点であることが分かる。
あとは、\(\small \displaystyle \frac{2}{3}<u+v<1\)の条件から、\(\small \displaystyle u+v=\frac{2}{3}\)のラインに下限が設定されていることから、下図のような範囲が点\(\small \mathrm{P}\)の存在範囲になる。
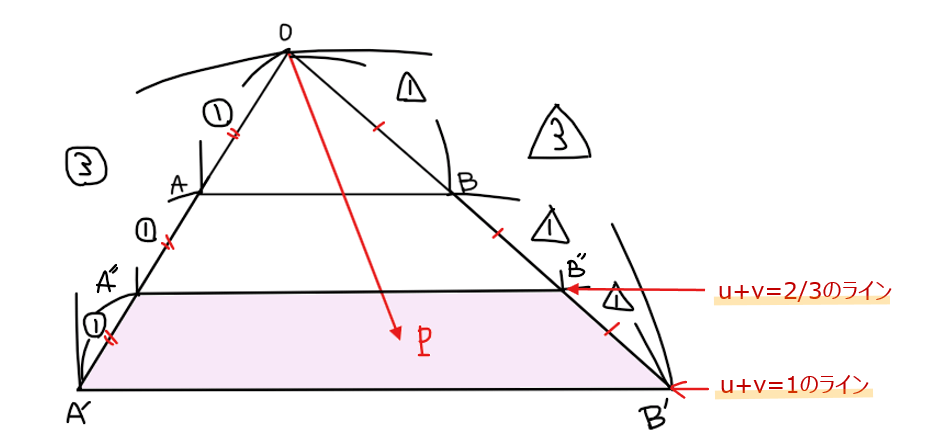
あとは、境界に気を付けながら図示した範囲を言語化すればよいでしょう。
点\(\small \mathrm{P}\)は上図の四角形\(\small \mathrm{A’A”B”B’}\)の内部および辺\(\small \mathrm{A’A”、B’B”}\)上(ただし、点\(\small \mathrm{A’、A”、B’、B”}\)を除く)…(答)。
●補足
たとえば、\(\small v=0\)のとき、条件式は\(\small \displaystyle \overrightarrow{OP}= u\overrightarrow{OA’}\space (\frac{2}{3}<u<1)\)は、辺\(\small \mathrm{A’A”}\)上(端点を除く)、同様に\(\small u=0\)のとき、条件式は\(\small \displaystyle \overrightarrow{OP}= v\overrightarrow{OB’}\space (\frac{2}{3}<v<1)\)は、辺\(\small \mathrm{B’B”}\)上(端点を除く)にあることから、これらの範囲は点\(\small \mathrm{P}\)の存在範囲に含まれる点に注意しよう。
3.3【問題3(応用)】係数の差が条件になっている場合の対処
三角形OABにおいて、\(\small s≧0,t≧0\)(s,tは実数)とし、\(\small \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)を考える。このとき、\(\small s-t=1\)の場合の終点Pの存在範囲を図示せよ。
最後は、解説編の基本パターン2に近い形をしていますが、係数の差になっているため、すこし考え方が応用的になります。ただし、解説編で紹介した内分点、外分点の公式を理解できていればそれほど難しくはないので、最後の一息、頑張って理解していきましょう!
まず、係数の和=1の形にするため、\(\small u=s,v=-t\)とおき直します。sは置き直す必要がないですが、解説の都合上置き換えています。
すると条件式は、\(\small u≧0、v≦0、u+v=1\)となります。\(\small \overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)も、
$$
\begin{equation}
\begin{split}
& \overrightarrow{OP}=u\overrightarrow{OA}-v\overrightarrow{OB}\\
& \overrightarrow{OP}=u\overrightarrow{OA}+v(-\overrightarrow{OB})\\
\end{split}
\end{equation}
$$
と書き直せます。ここで、\(\small \overrightarrow{OC}=-\overrightarrow{OB}\)とおくと、上式は、\(\small \overrightarrow{OP}=u\overrightarrow{OA}+v\overrightarrow{OC}\)となります。
一旦、置き換え後の条件を整理すると、\(\small u≧0、v≦0、u+v=1\)として\(\small \overrightarrow{OP}=u\overrightarrow{OA}+v\overrightarrow{OC}\)で表される点Pの存在範囲は?という問題を考えればokということなります。これは解説編の基本パターン2と殆ど同じですが、ベクトル\(\small OC\)の係数が「\(\small v≦0\)」という部分だけが異なります。基本パターン2ではベクトルの係数はいずれもゼロ以上でした。この違いは何を意味するのでしょうか?
解説を注意深く読んでいた人であれば、「そういえば基本パターン2の解説の時に、外分点を表すときはベクトルの係数が負になっていた!」ということに気づいたかもしれません(忘れていた人はもう一度見返してみましょう!)。実は、外分点の場合は、ベクトルの係数がマイナスになります。
■外分点の公式(再掲)
三角形OABの辺ABを\(\small m:n\)に外分する点Pは
$$\overrightarrow{OP}=-\frac{n}{m-n}\overrightarrow{OA}+\frac{m}{m-n}\overrightarrow{OB}$$
少しベクトルの係数が分かりやすいように分数を分けていますが、解説編の公式と同じ式です。今考えている式が\(\small \overrightarrow{OP}=u\overrightarrow{OA}+v\overrightarrow{OC}\)なので、\(\small u\)が\(\small -\frac{n}{m-n}\)、\(\small v\)が\(\small \frac{m}{m-n}\)に対応しています。
ここで、\(\small v≦0\)ということは、公式の\(\small \overrightarrow{OB}\)の係数\(\small \frac{m}{m-n}\)がマイナスになるということです。そのためには、\(\small m,n\)は正の値なので、分母の\(\small m-n\)がマイナスとなっている必要があります。このとき、公式の\(\small \overrightarrow{OA}\)の係数\(\small -\frac{n}{m-n}\)は先頭のマイナスと\(\small m-n\)のマイナスが打ち消し合って自動的にプラスになるので、今回考えている\(\small u≧0、v≦0\)という条件とも合致します。
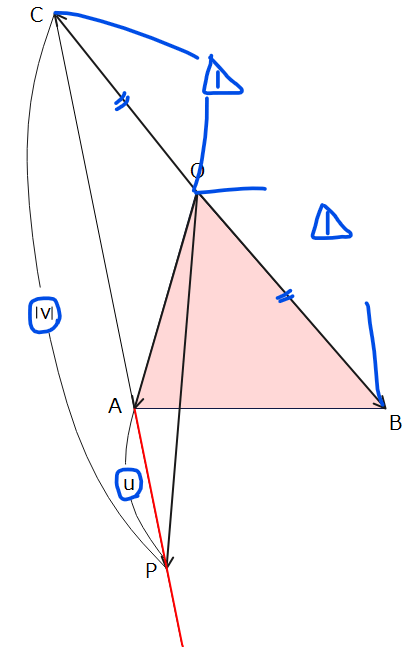
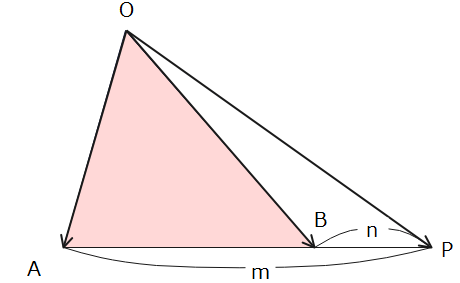
そして、\(\small m-n\)がマイナスということは\(\small m\)よりも\(\small n\)が大きいということで、図形的には辺ABを\(\small m:n\)に外分するときに点A側に外れてから点Bの方に戻ってくるような外分をすることを意味しています(下図参照)。
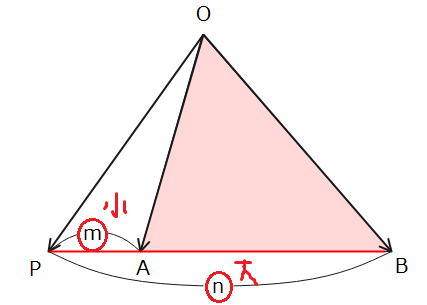
以上の考察から、\(\small \frac{m}{m-n}≦0\)という図形的な意味は、「上図のような△OABに対して、線分ABを上図のように\(\small m:n\)に外分する位置に点Pが存在する」ということが分かったのでこの考え方を今回の問題にも適用します。
\(\small \overrightarrow{OP}=u\overrightarrow{OA}+v\overrightarrow{OC}\)で\(\small v≦0\)ということは、\(\small \overrightarrow{OC}=-\overrightarrow{OB}\)と定義していたことから、下図のように点Oを基準として点Bと反対側にとった点がCです。△OACにおいて線分ACを点Cと反対側に外れて\(\small u:|v|\)(細かいですが\(\small v≦0\)なので絶対値を付けておく)に外分する点の集合が点Pであることから、点Pの存在範囲は、点Aを始点として、直線ACを点Cと反対側に伸ばした半直線上…(答)。
【おまけ】外分点の公式の補足
最後に証明するといっていた「外分点の公式では、必ずどちらかの係数がマイナスになる」の解答だけ最後におまけとして載せておきます。いろいろな証明方法があるので他にも探してみるとよいかもしれません。
証明)\(\small m>0,n>0,m≠n\)として、△OABの外分点Pの公式は一般に
$$\overrightarrow{OP}=-\frac{n}{m-n}\overrightarrow{OA}+\frac{m}{m-n}\overrightarrow{OB}$$
と表される。必ずどちらかの係数がマイナスということは、2つの係数を掛け算した結果が常にマイナスであることを示せばよいので、
$$-\frac{n}{m-n} \times \frac{m}{m-n}=-\frac{mn}{(m-n)^2}<0 $$
(証明終わり).
なので、ベクトルの係数の和が1で片方がマイナスになっていたら、外分点だなって覚えておくのもありですね。
本記事のまとめ
今回は、終点の存在範囲について、基本パターン3選とそれを使った問題3つを紹介しましたがいかがでしたか?
終点の存在範囲の問題は、平面上のベクトルは、2つのベクトルを何倍かして足し合わせれば表せるということから、足し合わせた結果のベクトル、すなわち終点がどの範囲に存在するのかを計算するというものなので、2つのベクトルの係数の条件に注目して解いていこうという流れでした。
大学入試などではそれほど出てこない分野ですが、定期試験では出てくると思うので、しっかり理解して点数をとれるようにしておきましょう。
では、本日はここまでです。お疲れさまでした!







コメント
問題2の解説、違くないですか?
コメントいただきありがとうございます。
ご指摘の通り、問題2の解説に誤りがありましたので、解説を修正しています。大変申し訳ございません。
今後も可能な限り正確な解説を心掛けてまいりますので、引き続きよろしくお願いします。