【数Ⅲ】式変形して区分求積法を利用する超難問（2003年京大理系後期を分かりやすく解説）

本記事では、2003年京都大学理系後期で出題された区分求積法の超難問について、分かりやすく解説していきたいと思います。この問題は、説明するよりも実際に解いて見てもらう方が分かると思いますが、明らかに区分求積法を利用して極限を求める問題なのですが、うまく区分求積法が使える形になっていないというところが最難関ポイントとなっています。

今回はこの問題を通して区分求積法と極限の問題を解くコツについても併せて解説していきますので、是非一緒に挑戦して理解を深めていきましょう！

• 極限と積分の難問に挑戦したい人
• 区分求積法の問題を極めたい人
• 極限と積分の面白い問題を理解したい人
• 極限・積分分野の大学入試対策をしたい人

【問題＆解説】式変形して区分求積法を利用する超難問

問題編（難易度：★★★）

解説編（考え方を分かりやすく解説）

問題を見た第一印象として、「極限（lim）」「シグマ（\(\small \sum\)）」「\(\small k/n\)を含む関数」から、区分求積法を利用する問題と気づければ第一関門はクリア。でも、区分求積法を利用する場合、積分の「dx」に相当する微小幅である「1/n」が必要となるが本問では見当たらない…が、式変形していくうちに出てくればラッキーとして一旦忘れておこう。

まずは、手始めにどこから攻めるかだが、シグマの中にある「\(\small (-1)^k\)」という係数も地味に扱いずらいので、シグマの和を偶数項目と奇数項目に分けて「\(\small (-1)^k\)」を＋の項と－の項に分割しておこう。

\begin{split}
\small \displaystyle \lim_{n \to \infty} \sum_{k=1}^{2n}(-1)^k\left(\frac{k}{2n}\right)^{100}\\
\end{split}

において、偶数番目の項（\(\small k=2,4,\cdots,2n\)）は、\(\small k=2\ell \space (\ell =1,2,\cdots,n)\)とすれば、

\begin{split}
&\small \displaystyle \lim_{n \to \infty} \sum_{\ell=1}^{n}(-1)^{2\ell}\left(\frac{2\ell}{2n}\right)^{100}\\
&\small \displaystyle =\lim_{n \to \infty} \sum_{\ell=1}^{n}\left(\frac{\ell}{n}\right)^{100}\\
\end{split}

一方で、奇数番目の項（\(\small k=1,3,\cdots,2n-1\)）は、\(\small k=2\ell-1 \space (\ell =1,2,\cdots,n)\)とすれば、

\begin{split}
&\small \displaystyle \lim_{n \to \infty} \sum_{\ell=1}^{n}(-1)^{2\ell-1}\left(\frac{2\ell-1}{2n}\right)^{100}\\
&\small \displaystyle =- \lim_{n \to \infty} \sum_{\ell=1}^{n}\left(\frac{\ell}{n}-\frac{1}{2n}\right)^{100}\\
\end{split}

よって、

\begin{split}
&\small \displaystyle \lim_{n \to \infty} \sum_{k=1}^{2n}(-1)^k\left(\frac{k}{2n}\right)^{100}\\
&\small \displaystyle =\lim_{n \to \infty} \sum_{\ell=1}^{n} \bigg[\left(\frac{\ell}{n}\right)^{100}-\left(\frac{\ell}{n}-\frac{1}{2n}\right)^{100}\bigg]\\
\end{split}

さて、ここから辺で手が止まる人が多くなってくると思います。100乗の差なので第2項目を2項展開して式を整理するのか、ここから1/nをどうにか括り出して区分求積法の形に持って行くのか…。あれこれ試していくうちに、「この和の極限を直接求めることはできないのでは？」ということに気が付けるとgood！

直接求められない極限の求め方は、はさみうちの原理（または追い出しの原理）を利用すればOKでした。本問では、区分求積法を\(\small f(x)=x^{100}\)として利用することが推測できるので、\(\small \displaystyle \frac{\ell}{n}-\frac{1}{2n}≦x≦\frac{\ell}{n}\)の範囲ではさみうちの原理が利用できないかを考えてみます。

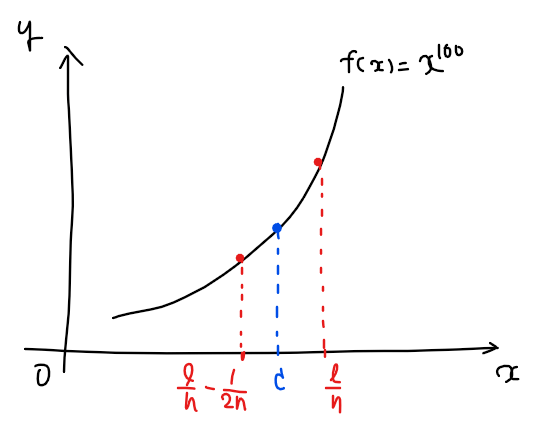
関数と定義域をグラフで図示すると上図のようになることから、\(\small x>0\)の範囲[*1]では、明らかに

\begin{split}
&\small \displaystyle f\left(\frac{\ell}{n}-\frac{1}{2n}\right)<f(c)<f\left(\frac{\ell}{n}\right)
\end{split}

を満たす実数\(\small c\)が存在する。

*1：補足
\(\small f(x)=x^{100}\)は、\(\small x<0\)の範囲では、\(\small f(-1)=1,f(-2)=2^{100}\)のように単調減少になるので、\(\small x\)の正負で場合分けが必要。このあたりは自明としてよいと思うが、厳密に増減を確認しておきたければ\(\small f^{(2)}(x)\)（2階微分）を計算すればよいでしょう。

この形は中間値の定理に酷似していることから、上記の範囲で中間値の定理を考えてみよう。

関数\(\small f(x)=x^{100}\)は、\(\small \displaystyle \frac{\ell}{n}-\frac{1}{2n}≦x≦\frac{\ell}{n}\)で連続かつ微分可能なので、中間値の定理より
\begin{split}
&\small \displaystyle \frac{ f\left(\dfrac{\ell}{n}\right)-f\left(\dfrac{\ell}{n}-\dfrac{1}{2n}\right)}{\dfrac{\ell}{n}-\left(\dfrac{\ell}{n}-\dfrac{1}{2n} \right)}=f^{\prime}(c_\ell) \quad \cdots ②\\
\end{split}
を満たす実数\(\small c_\ell\)が\(\small \displaystyle \frac{\ell}{n}-\frac{1}{2n}≦c_\ell≦\frac{\ell}{n}\)に存在する。

式②を具体的に計算すると

\begin{split}
&\small \displaystyle \frac{ f\left(\dfrac{\ell}{n}\right)-f\left(\dfrac{\ell}{n}-\dfrac{1}{2n}\right)}{\dfrac{\ell}{n}-\left(\dfrac{\ell}{n}-\dfrac{1}{2n} \right)}=f^{\prime}(c_\ell) \\
\small \Leftrightarrow \space &\small \displaystyle \left(\dfrac{\ell}{n}\right)^{100}-\left(\dfrac{\ell}{n}-\dfrac{1}{2n}\right)^{100}=\dfrac{1}{2n}f^{\prime}(c_\ell) \\
\small \Leftrightarrow \space &\small \displaystyle \sum_{\ell=1}^{n}\bigg[ \left(\dfrac{\ell}{n}\right)^{100}-\left(\dfrac{\ell}{n}-\dfrac{1}{2n}\right)^{100}\bigg]=\dfrac{1}{2n} \sum_{\ell=1}^{n} f^{\prime}(c_\ell)\\
\end{split}

よって、求める極限は

\begin{split}
&\small \displaystyle \lim_{n \to \infty} \sum_{\ell=1}^{n}\bigg[ \left(\dfrac{\ell}{n}\right)^{100}-\left(\dfrac{\ell}{n}-\dfrac{1}{2n}\right)^{100}\bigg]\\
&\small \displaystyle =\lim_{n \to \infty} \dfrac{1}{2n} \sum_{\ell=1}^{n} f^{\prime}(c_\ell)\\
\end{split}

あとは、

\begin{split}
&\small \displaystyle \frac{\ell}{n}-\frac{1}{2n}≦c_\ell≦\frac{\ell}{n}\\
\small \Leftrightarrow \space &\small \displaystyle \frac{2\ell-1}{2n}≦c_\ell≦\frac{2\ell}{2n}
\end{split}

より、\(\small \displaystyle 0<\frac{2\ell-1}{2n}\)であることから、\(\small x>0\)の範囲で関数 \(\small f^{\prime}(x)=100x^{99}\)は単調増加となるため

\begin{split}
\small \displaystyle f^{\prime}\left(\frac{\ell}{n}-\frac{1}{2n}\right) &\small \displaystyle ≦f^{\prime}\left(c_\ell\right)≦ f^{\prime}\left(\frac{\ell}{n}\right)\\
\small \Leftrightarrow \space \displaystyle \lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n} f^{\prime}\left(\frac{\ell}{n}-\frac{1}{2n}\right) &\small \displaystyle≦ \lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n}　f^{\prime}\left(c_\ell\right)≦ \lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n} f^{\prime}\left(\frac{\ell}{n}\right)\\
\end{split}

あとは、上式の両端の極限を区分求積法で計算すればOKです。

\begin{split}
\small (右辺) &\small \displaystyle =\lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n} f^{\prime}\left(\frac{\ell}{n}\right)\\
&\small \displaystyle =\frac{1}{2}\int _0^1 f^{\prime}(x)dx\\
&\small \displaystyle =\frac{1}{2}\bigg[f(x)\bigg]_0^1 \quad ◀微分の積分は元の関数\\
&\small \displaystyle =\frac{1}{2}\bigg[f(1)-f(0)\bigg]\\
&\small \displaystyle =\frac{1}{2}(1^{100}-0) \quad ◀f(x)=x^{100}\\
&\small \displaystyle =\frac{1}{2}\\
\end{split}

左辺も同様に計算すると

\begin{split}
\small (左辺) &\small \displaystyle =\lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n} f^{\prime}\left(\frac{\ell}{n}-\frac{1}{2n}\right) \\
&\small \displaystyle =\frac{1}{2}\int _0^1 f^{\prime}(x)dx\\
&\small \displaystyle =\frac{1}{2}\\
\end{split}

よって、はさみうちの原理より

\begin{split}
\small \displaystyle \lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n}　f^{\prime}\left(c_\ell\right) =\color{red}{\frac{1}{2} \space \cdots 【答】}\\
\end{split}

本記事のまとめ

今回は京大の超難問な区分求積法を利用する極限の問題を解説してきましたが、いかがでしたか？区分求積法がうまく適用できない場合は、はさみうちの原理を利用して評価するという考え方を教えてくれる良問でした。

多くの問題でははさみうちの原理を利用する場合は、その前段に誘導問題として利用する不等式を証明させる問題がセットですが、今回はその誘導がなかったので結構大変だったかなと思います。

京大くらいのレベルになると誘導がなくてもはさみうちの原理を利用するためにうまい不等式を用意する力が求められるわけですね（鬼畜…）。

最後に、そんな鬼畜レベルな難問のエッセンスだけ抽出した類題を解いて終わりにしましょう。

【類題】中間値の定理を利用した区分求積法

関数 \(\small \displaystyle f(x)=x^{x^x}\)とすると

\begin{split}
&\small \displaystyle \lim_{n \to \infty} \sum_{k=1}^{2n}(-1)^k \left(\frac{k}{2n}\right)^{{\left(\frac{k}{2n}\right)}^{\left(\frac{k}{2n}\right)}}\\
=&\small \displaystyle \lim_{n \to \infty} \sum_{\ell=1}^{n}\left[f\left(\frac{\ell}{n}\right)-f\left(\dfrac{\ell}{n}-\dfrac{1}{2n}\right)\right] \quad \cdots ①\\
\end{split}

ここで、\(\small f(x)\)は連続かつ微分可能であることから、中間値の定理より

\begin{split}
&\small \displaystyle f\left(\frac{\ell}{n}\right)-f\left(\frac{\ell}{n}-\frac{1}{2n}\right)=\frac{1}{2n}f^{\prime}(c_\ell)
\end{split}

を満たす実数\(\small c_\ell\)が\(\small \displaystyle \frac{\ell}{n}-\frac{1}{2n}≦c_\ell≦\frac{\ell}{n}\)に存在する。

よって、式①は

\begin{split}
&\small \displaystyle \lim_{n \to \infty} \sum_{\ell=1}^{n}\left[f\left(\frac{\ell}{n}\right)-f\left(\dfrac{\ell}{n}-\dfrac{1}{2n}\right)\right] \\
＝&\small \displaystyle \lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n}f^{\prime}(c_\ell)\\
\end{split}

今、\(\small n\to\infty\)より、\(\small \displaystyle \frac{\ell}{n}-\frac{1}{2n}≦c_\ell≦\frac{\ell}{n}\)を十分に狭くとることができることから、関数 \(\small f^\prime(x)\)の増減によって、\(\small \displaystyle f^\prime\left(\frac{\ell}{n}-\frac{1}{2n}\right)\)、\(\small \displaystyle f^\prime\left(\frac{\ell}{n}\right)\)の大小関係こそ変わる可能性はあるが、\(\small \displaystyle f^\prime\left(c_\ell \right)\)が両者の間に位置することは変わらない。

この事実と、\(\small n \to \infty\)の極限において

\begin{split}
&\small \displaystyle \lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n}f^\prime \left(\frac{\ell}{n}-\frac{1}{2n}\right) \\
＝&\small \displaystyle \lim_{n \to \infty} \frac{1}{2n}\sum_{\ell=1}^{n}f^\prime \left(\frac{\ell}{n}\right) \\
=&\small \displaystyle \frac{1}{2}\int_0^1f^\prime (x)dx\\
=&\small \displaystyle \frac{1}{2}\bigg[x^{x^x} \bigg]_0^1\\
=&\small \displaystyle \frac{1}{2}\\
\end{split}

であることから、はさみうちの原理より、求める極限値は\(\small \displaystyle \color{red}{\frac{1}{2}\cdots【答】}\)である。

では今回はここまでです。お疲れさまでした！