【整数問題】ax+by=c型の不定方程式の解き方（裏ワザあり！？ユークリッド互除法、合同式の利用）

今回は、1次不定方程式の解き方について、パターン別に解説していきます。「不定方程式を簡単に解くコツってないの？」という疑問を持っている人向けに、一般的に知らているユークリッド互除法や合同式を利用した解法から、あまり知られていない裏ワザの紹介まで解説しているので、ぜひ最後まで読んでみてください！

　本記事はこんな人におすすめ

自分で求めた不定方程式の解が正しいのか確認する方法が知りたい
ユークリッド互除法を使った不定方程式の解き方が知りたい
合同式を使った不定方程式の解き方が知りたい
不定方程式を簡単に解ける裏ワザを知りたい

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

【はじめに】不定方程式とは？
【徹底解説】不定方程式の解き方・考え方の基礎
特殊解が見つけずらい場合の対処法
1. 例題3：特殊解がすぐにわからない不定方程式
【問題＆解説】不定方程式の演習問題
本記事のまとめ

【はじめに】不定方程式とは？

こんにちは。数尾学（かずおまなぶ）です。

どうも！hiroemonです！今回は不定方程式について解説していきます。

今日のテーマの不定方程式ってなんだか難しそうな名前だけど、どんな方程式なの？

じゃあまずは「不定方程式とはなにか」というところから確認していこうか！

■不定方程式ってなに？
→答えを1つに決めることができない方程式のこと

そんな優柔不断そうな方程式があるんですか？

まぁ、ちょっと違うけど…。でも、はじめはそんなイメージでokです。

でも、答えが1つに決まらないってどういうこと？

たとえば、カズオくん。この方程式はとけるかな？
\begin{cases}
x+y=3\\
x-y=1\\
\end{cases}

先生、さすがに僕でもこれは解けますよー！答えは$\small x=2、y=1$でしょ？

大正解！じゃあこれは？
$$\small 2x+y=1\mathbf{の整数解を求めよ}$$

えっと、連立方程式にしては式が1つ足りないなぁ。先生！問題ミスあります！

これは、問題ミスじゃなくって、本当に式は1つだけだよ！

えっ！？ん…、1つだけじゃ、答えが求められないですよ。

実はこの「$\small 2x+y=1$の整数解を求めよ」という問題が不定方程式だね。カズオくんのいう通りこの方程式は答えを1組に絞ることはできない。でも、「こんな条件を満たすものが答えになります！」という候補なら求めることができるんだ！この解の候補を求めることが不定方程式を解くということになるよ。

答えの候補を求めるってどういうことか全然イメージわかないんですけど…。

そしたら、次章以降で不定方程式の具体的なパターンや解き方を一緒に見ていこうか！

【徹底解説】不定方程式の解き方・考え方の基礎

では、ここからは不定方程式の解き方と考え方のコツを解説していきます。

【基本パターン】不定方程式の基礎知識

不定方程式の解き方にはいくつかパターンや解法がありますが、基本は常に1つだけなので、まずはこれを理解しましょう！

■不定方程式の基本パターン
等式
$$ax=by$$
で $\small a$と$\small b$が互いに素ならば
$$\color{red}{x=bk,\space y=ak\space (k\mathbf{は整数})}$$
　が成り立つ。

（補足）互いに素ってなんだっけ？
「2と5」や「4と15」のように同じ数では割れない数同士のこと。
逆に、「3と9」はどちらも3で割れるし、「15と20」はどちらも5で割れるので、互いに素ではない。

どういうことか、具体的に$\small 2x=3y$を例に解説します。この式は「2×□=3×△」が成り立つような□と△に入る数字は？という問題です。答えは無限にあって、「□=3、△=2」や「□=6、△=4」、「□=-9、△=-6」などなど。

ここで□と△に入る数にはある共通点があることに気づきます。それは□は3の倍数、△は2の倍数になるということ。なので、$\small x=3k$、$\small y=2k$と表せるよ、ということです。

なぜこのようになるのかというと、$\small 2x=3y$は、左辺は2の倍数（$\small 2x$は2×□の形だから）、右辺は3の倍数ですが、通常、2の倍数と3の倍数はイコールにはなりません。

2の倍数＝$\small 2,4,\color{blue}6,8,10,\color{blue}{12},\cdots$
3の倍数=$\small 3,\color{blue}6,9,\color{blue}{12},\cdots$

でも、これらが$\small 2x=3y$という等式でイコールになるときがあって、それが両辺が$\small 2 \times 3 =6$の倍数になるときです。$\small 2x$が6の倍数になるということは、$\small x$が3の倍数になりますし、$\small 3y$が6の倍数になるということは、$\small y$が2の倍数になるわけです。

（補足）$\small a$、$\small b$が互いに素じゃないといけないの？
たとえば、
$$8x=6y$$
のように、$\small a$、$\small b$が互いに素ではない場合、$\small x=3, y=4$のような組み合わせも答えになってしまい、必ずしも$\small x$が6の倍数、$\small y$が8の倍数ではなくてもよくなってしまいます。そのため、互いに素になっていることが重要です。

（補足）答えは$\small x=3k$、$\small y=2k’$にはならないの？
よくある質問ですがこれは間違い。理由は、$\small \color{red}{x=3k}$とおくと、$\small y$の値は$\small 2x=3y$に代入することで
\begin{equation}
\begin{split}
2\cdot \color{red}{3k}&=3y\\
2k&=y
\end{split}
\end{equation}
となるので、必ず$\small y=2k$となります。

このあと、不定方程式の代表パターンを2つ紹介しますが、いずれもこの基本パターンに帰着させて解く考え方になります。

【パターン1】$\small ax+by=1$型の解法のポイント

■$\small ax+by=1$型の不定方程式の解き方
・STEP1：特殊解を見つける
・STEP2：『（与式）$\small -$（特殊解の式）』で基本パターンに持ち込む

では具体的な方法を例題で確認していきます。

【例題1】$\small ax+by=1$の具体的な解き方

例題1：$\small ax+by=1$型の解法

方程式$\small 4x+7y=1$の整数解をすべて求めよ。

　解説

STEP

特殊解を見つける

まずはじめは、問題の方程式$\small 4x+7y=1$を満たす$\small (x,y)$をなんでもいいので1つ探します。すると、たとえば$\small (x,y)=(2,-1)$が見つかります。$\small 4\cdot \color{red}2+7\cdot\color{red}{(-1)}=8-7=1$となり、確かに方程式の解になっていますね。

STEP

『（与式）$\small -$（特殊解の式）』で基本パターンに持ち込む

与式とは、『$\small 4x+7y=1$』のこと。特殊解の式とは、与式にSTEP1で求めた特殊解を代入した式、すなわち『$\small 4\cdot \color{red}{2}+7\cdot\color{red}{(-1)}=1$』のことを指しています（ネーミングは私が勝手につけたのでご認識を…）。

与式から特殊解の式を引き算すると

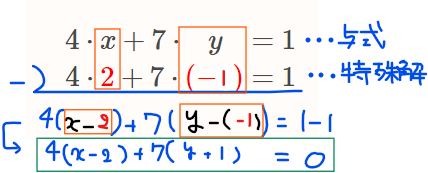
\begin{equation}
\begin{split}
4(x-2)+&7(y+1)=0\\
4(x-2)&=-7(y+1)\\
\end{split}
\end{equation}

（補足）引き算の式変形が苦手な人へ
数字のまま引き算する式変形が苦手な人は、特殊解を$\small 2=x’$、$\small -1=y’$と文字で置いて、特殊解の式を$\small 4\color{red}{x’}+7\color{red}{y’}=1$としたうえで引き算してあげると計算しやすいと思います。
\begin{equation}
\begin{split}
(4x+7y)-(4x’+7y’)&=1-1\\
4x-4x’+7y-7y’&=0\\
4(x-x’)+7(y-y’)&=0\\
4(x-\color{red}{x’})=-7&(y-\color{red}{y’})\\
4(x-\color{red}{2})=-7&(y-\color{red}{(-1)})\\
4(x-2)=-7&(y+1)\\
\end{split}
\end{equation}

$\small x-2=X$、$\small y+1=Y$とおいてあげれば、

$$4X=-7Y\quad\cdots(*)$$

となり、基本パターンの形になります(慣れている人はわざわざ$\small X、Y$とおかなくてOK)。

4と7は互いに素なので、$\small X=7k$（$\small k$は整数）、つまり、$\small x-2=7k$となるので、$\small \color{red}{x=7k+2}$と表せます。$\small (*)$に$\small X=7k$を代入してあげると、

\begin{equation}
\begin{split}
4\cdot\color{red}{(7k)}&=-7Y\\
-4k&=Y\\
\end{split}
\end{equation}

よって、$\small y+1=-4k$、すなわち $\small \color{red}{y=-4k-1}$と求まります。

（解答）
$\small \quad x=7k+2,\space y=-4k-1$($\small k$は整数)

【補足説明】自分の答えが解答と違うときの検算の方法は？

不定方程式の解は、特殊解を何にするかによって解答の表現が変わります。実際には同じ答えを表していても答えの見え方が変わってしまうわけですね。

たとえば、例題1の問題で特殊解として$\small x=9,y=-5$を選んだ場合、答えは$\small \color{red}{x=7k+9,\space y=-4k-5}$となります。もちろんこれも正解です。

ただ、参考書などの解答は1つしかかかれないので、自分の答えがあっているか不安になりますよね。そんなときは、次の方法で確かめましょう！

■自分の答えを確かめる方法
　$\small k=0、1$のときの$\small x,y$を問題の式に代入して成り立つか確認せよ！
　（$\small k=0$というのは『$\small x=$〇$\small k$+★』の★部分が$\small x$の特殊解になっているかということ（$\small y$も同様））

たとえば、例題1であれば解答の$\small x=7k\color{red}{+2},\space y=-4k\color{blue}{-1}$で$\small k=0$とすると、$\small x=\color{red}{+2}$、$\small y=\color{blue}{-1}$となり、確かに特殊解になっていますね。

$\small k=1$のときは、$\small (x,y)=(9,-5)$なりますが、問題文左辺に代入すると

\begin{equation}
\begin{split}
(左辺)&=4x+7y\\
&=4\cdot9+7\cdot(-5)\\
&=36-35\\
&=1=(右辺)\\
\end{split}
\end{equation}

となり成り立つので、これで検算完了です。

この検算方法は、今回のパターンに限らずどんな不定方程式のパターンでも使えるのでぜひ活用してみてください！

【パターン2】$\small ax+by=c$ 型の解法のポイント

■$\small ax+by=c$ 型の不定方程式の解き方
解き方の方針は$\small ax+by=1$と同じだが、
特殊解の見つけ方がSTEP1、2の2段階になるのがポイント！
・STEP1：$\small ax+by=1$の特殊解(仮の特殊解)を見つける
・STEP2：仮の特殊解を$\small c$倍して真の特殊解とする
・STEP3：『（与式）$\small -$（真の特殊解の式）』で基本パターンに持ち込む

【例題2】$\small ax+by=c$ の具体的な解き方

例題2：$\small ax+by=c$ 型の解法

方程式$\small 11x+2y=5$の整数解をすべて求めよ。

　解説

STEP

$\small ax+by=1$の特殊解(仮の特殊解)を見つける

まずは、$\small 11x+2y=\color{red}1$の特殊解を見つけます。たとえば、$\small (x,y)=(1,-5)$があてはまるので、これを仮の特殊解とします。

STEP

仮の特殊解を$\small c$倍して真の特殊解とする

$\small (x,y)=(1,-5)$を5倍（$\small 11x+2y=\color{red}5$の5）した$\small (x,y)=(5,-25)$が$\small 11x+2y=5$の特殊解になります。実際に代入してみると、

\begin{equation}
\begin{split}
11x+2y&=11\cdot \color{red}5+2\cdot\color{red}{(-25)}\\
&=55-50\\
&=5\\
\end{split}
\end{equation}

となり確かに特殊解になっていることが確認できますね。

（補足）なぜ仮の特殊解を$\small c$倍すると求める不定方程式の特殊解になるのか？
$\small ax+by=c$の仮の特殊解を$\small (x,y)=(m,n)$とすると、仮の特殊解の定義より$\small am+bn=1\cdots①$。ここで①の式全体を$\small c$倍すると
\begin{equation}
\begin{split}
c(am+bn)&=c\cdot1\\
a(\color{red}{cm})+b(\color{red}{cn})&=c\\
\end{split}
\end{equation}
上式は、$\small (x,y)=(cm, cn)$が不定方程式 $\small ax+by=c$の特殊解であることを示しているので、仮の特殊解 $\small (x,y)=(m,n)$と見比べると$\small c$倍したものが真の特殊解になっていることが分かります。

STEP

『（与式）$\small -$（真の特殊解の式）』で基本パターンに持ち込む

特殊解が分かったのであとはパターン1の解き方と同じです。

\begin{equation}
\begin{split}
11x\space\space\space+\qquad 2y\space\space\space&=5\quad \cdots①\\
11\cdot \color{red}5+2\cdot\color{red}{(-25)}&=5\quad \cdots②\\
\end{split}
\end{equation}

①-②より

\begin{equation}
\begin{split}
11(x-5)&+2(y+25)=0\\
11(x-5)&=-2(y+25)\quad \cdots ③\\
\end{split}
\end{equation}

11と2は互いに素なので、$\small x-5=2k$（ただし、$\small k$は整数）より、$\small \color{red}{x=2k+5}$。この結果を③に代入することで

\begin{equation}
\begin{split}
11\cdot\color{red}{(2k)}&=-2(y+25)\\
11k&=-(y+25)\\
\color{red}y&\color{red}{=-11k-25}\\
\end{split}
\end{equation}

（解答）
$\small \quad \color{red}{x=2k+5,\space y=-11k-25}$($\small k$は整数)

特殊解が見つけずらい場合の対処法

ここまでで、不定方程式の解き方の基礎固めはできたのでここからはいよいよ実践編に入ります。これまでの例題では特殊解を自力で見つけてきましたが、$\small x,y$の係数が大きくなるにつれて特殊解が見つけずらくなります。そんな場合の対処法を身につけましょう！

例題3：特殊解がすぐにわからない不定方程式

方程式$\small 155x＋42y＝1$の整数解をすべて求めよ。

■特殊解の見つけ方
　・方法1：自力で見つける
　・方法2：ユークリッドの互除法を利用
　・方法3：簡易的互除法の利用　※おすすめの裏ワザ
　・方法4：合同式の利用

ここでは、例題3のような問題に対して自力で特殊解を見つける方法以外に、特殊解が見つけずらい場合の対処方法を3つ紹介します。裏ワザ的方法もあるのでしっかりと理解して使いこなせるようになりましょう。

【対処法1】ユークリッドの互除法の利用

■ユークリッドの互除法を使った特殊解の求め方
　・STEP1：割る数と余りで繰り返し割り算し、
　　　　　　元の数と余りの関係式を作る（余りが1になったら終了）
　・STEP2：関係式を「余り=…」の形に変形
　・STEP3：「余り＝…」の式を繰り返し代入して問題文の方程式を復元

$\small 155x＋42y＝1$を満たす特殊解をぱっと見で見つけるのは大変です。そんなときは、ユークリッドの互除法が利用できます。一番よく使われている解法になります。

では、ユークリッドの互除法を利用した解き方を解説します。ユークリッドの互除法とは、一言でいうと『お互いに除（割り算）をしていく方法』です。$\small x,y$の係数をお互いに割り算していくことで特殊解を見つけることができます。

STEP

割る数と余りで繰り返し割り算し、元の数と余りの関係式を作る（余りが1になったら終了）

$\small x$の係数である$\small \color{red}{155}$と$\small y$の係数である$\small \color{blue}{42}$を使って、

\begin{equation}
\begin{split}
\color{red}{155}&=\color{blue}{42}\cdot3+\color{green}{29}\cdots①\\
\color{blue}{42}&=\color{green}{29}\cdot1+\color{red}{13}\cdots②\\
\color{green}{29}&=\color{red}{13}\cdot2+\color{blue}{3}\space\space\cdots③\\
\color{red}{13}&=\color{blue}{3}\cdot4+1\quad\cdots④\\
\end{split}
\end{equation}

のように、割る数と余りを使ってどんどん割り算を続けていき、最後に式④のように余りが1になったら終了します。

（補足）割り算の式と筆算の対応関係
①～④の式を出すときには筆算を利用します。例えば筆算と式①との対応関係は次の通りです。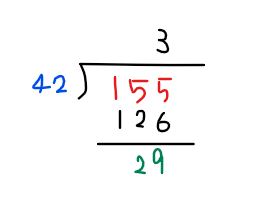

元の数、割る数、余りの関係式、(元の数)=(割る数)×(商)+(余り)を用いることで式①になります。

STEP

関係式を「余り=…」の形に変形

次に、①～④の式を「余り＝…」の形にします。

\begin{equation}
\begin{split}
\color{red}{155}&-\color{blue}{42}\cdot3=\color{green}{29}\cdots①\\
\color{blue}{42}&-\color{green}{29}\cdot1=\color{red}{13}\cdots②\\
\color{green}{29}&-\color{red}{13}\cdot2=\color{blue}{3}\space\space\cdots③\\
\color{red}{13}&-\color{blue}{3}\cdot4=1\quad\cdots④\\
\end{split}
\end{equation}

STEP

「余り＝…」の式を繰り返し代入して問題文の方程式を復元

そうしたら、③から順番に「余り＝…」の式を代入していきます。④に③を代入することで

\begin{equation}
\begin{split}
\color{red}{13}-(\color{green}{29}-\color{red}{13}\cdot2)\cdot4&=1\\
\color{red}{13}-\color{green}{29}\cdot4+\color{red}{13}\cdot8&=1\\
\color{red}{13}\cdot(1+8)-\color{green}{29}\cdot4&=1\\
\color{red}{13}\cdot9-\color{green}{29}\cdot4&=1\\
\end{split}
\end{equation}

（補足）式変形のコツ
・割る数と余り（式で青、赤、緑の数字）は計算せずに残しておく。
・同じ項が出てきたら文字式の計算の要領で一つの項にまとめる。
　例1：$\small 13\cdot\color{red}{3}+13\cdot\color{red}{5}=13\cdot\color{red}{8}$（13を3個と13を5個を足すと全部で13が8個になるということ）
　例2：$\small 13\cdot\color{red}{3}-13\cdot\color{red}{5}=13\cdot\color{red}{(-2)}$（13を3個から13を5個を引くと全部で13が-2個になるということ）

今度はこの式に②を代入して

\begin{equation}
\begin{split}
(\color{blue}{42}-\color{green}{29}\cdot1)\cdot9-\color{green}{29}\cdot4&=1\\
\color{blue}{42}\cdot9-\color{green}{29}\cdot9-\color{green}{29}\cdot4&=1\\
\color{blue}{42}\cdot9-\color{green}{29}\cdot13&=1\\
\end{split}
\end{equation}

今度はこの式に①を代入して

\begin{equation}
\begin{split}
\color{blue}{42}\cdot9-(\color{red}{155}-\color{blue}{42}\cdot3)\cdot13&=1\\
\color{blue}{42}\cdot9-\color{red}{155}\cdot13+\color{blue}{42}\cdot39&=1\\
-\color{red}{155}\cdot13+\color{blue}{42}\cdot48&=1\\
\color{red}{155}\cdot(-13)+\color{blue}{42}\cdot48&=1\\
\end{split}
\end{equation}

最後の式と問題の式 $\small 155x+42y=1$を見比べると、$\small (x,y)=(-13,48)$が特殊解になっていることが分かります。このようにしてユークリッドの互除法を使って特殊解を見つけることができます。

ここからの解き方は、パターン1と同じなので簡単に解説します。$\small 155x+42y=1$から$\small 155\cdot(-13)+42\cdot48=1$を引き算することで$\small 155(x+13)=-42(y-48)\cdots⑤$を得るので、$\small x+13=42k\cdots⑥$（$\small k$は整数）より、$\small \color{red}{x=42k-13}$。⑥を⑤に代入することで$\small \color{red}{y=-155k+48}$。

（解答）
$\small \quad \color{red}{x=42k-13,\space y=-155k+48}$（$\small k$は整数）

【対処法2】簡易的互除法の利用

『簡易的互除法』という名前は私が勝手につけてます…（なので覚えなくって大丈夫）。この方法はユークリッドの互除法がベースとなっているのですが、ユークリッドの互除法は関係式を代入しまくって元の式を復元する工程の計算が面倒なので、その手間を簡略化するために編み出された方法です。

やり方は言葉だと説明しにくいので、先のどの例題3を使って解きながら解説します。

まず、ユークリッドの互除法のときみたいにひたすら割り算をしていきます。このときにポイントとして、下のように横に筆算をかいていきます。

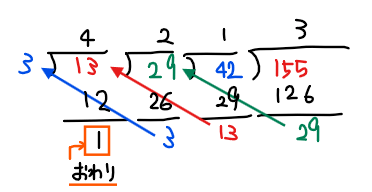
次に、下のように左上に「1」（赤丸箇所）をかき、その右に真下の数字をそのまま書きます（今回なら「4」）。

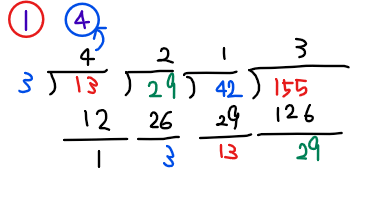
そうしたら、さらにその右側に数字をかいていくのですが、下のように、「右隣りと真下の数字を掛け算して、2つ右隣の数を足した数」を書きます（最初はちょびっと複雑かも…練習して慣らしましょう！）。

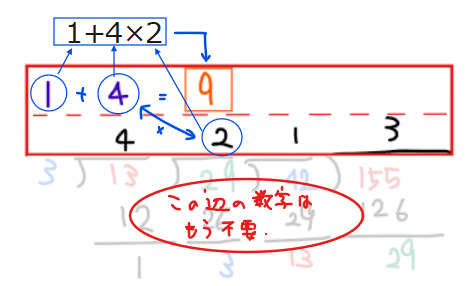
これを一番右端に到達するまで繰り返します。

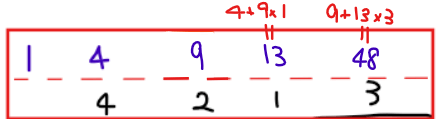
最後に残った右の2つの数字に$\small \pm$の符号をつけたものが特殊解の候補になります。今回であれば、$\small \pm 13, \pm 48$が特殊解の候補です。

ここで注意したいのが、「特殊解の候補」という点です。「$\small x$と$\small y$のどちらが13または48なのか？」、「符号はプラスなのかマイナスなのか？」は、問題文の式に代入して確かめる必要があります。

見つけ方にも一応コツがあって、かけ算の1の位だけ計算して問題文の右辺になるかを確認するのがおすすめです。どういうことかというと、今回の例であれば、$\small 155x+42y=1$なので、仮に$\small x=48,y=13$（一旦符号は置いておこう）だとすると、$\small 155 \times 48$の計算結果の1の位は「0」、$\small 42 \times 13$の計算結果の1の位は「6」なので足し引きしても絶対に右辺の1になりません。なので、$\small x=13,y=48$と決まります。符号は、$\small 155 \times 13$の計算結果の1の位は「5」、$\small 42 \times 48$は「6」なので、右辺が1になるためには「6-5=1」にならないといけないので、$\small 155 \times 13$の計算結果がマイナスになればよく、$\small x=-13$、$\small y=48$と決まります。

慣れないうちは面倒だと思うかもですが、慣れてしまえばユークリッドの互除法で解くよりも素早く簡単に解けるので覚えておくと便利です（検算にもつかえる）。

特殊解が見つかったのであとの解き方は、ユークリッドの互除法と同じなので割愛します。

【対処法3】合同式の利用

最後は、合同式(mod)を利用した解法です。先に伝えておくと、合同式を使った解法は若干勘頼みな手法なので個人的にはすごく便利というわけではないですが、合同式を使うことで特殊解と合わせて一気に一般解まで求めることができるので知っておいてもよいかと思います。

■合同式を用いた特殊解の求め方
　・STEP1：$\small x$と$\small y$の係数のうち絶対値が小さい方の数字$\small p$を法とする$\small \pmod p$
　・STEP2：合同式の性質を使ってうまく「$\small x \equiv$〇$\small \pmod p$」（または「$\small y \equiv$〇$\small \pmod p$」）の形をつくる

実際に例題3を合同式を使って解いてみます。

STEP

$\small x$と$\small y$の係数のうち絶対値が小さい方の数字$\small p$を法とする$\small \pmod p$

$\small 155x+42y=1$の係数を見ると、$\small y$の係数である42の方が小さいので42を法とする合同式を考えます。

（補足）合同式(mod)ってなんだっけ？
$\small a \equiv b \pmod{p}$というのは、整数$\small a$を$\small p$で割ったときの余りが$\small b$という意味を表しています。

$\small 155x+42y=1$を式変形すると、$\small 155x=\color{red}{-42y+1}$なので、$\small 155x$は42で割ると1余る数なので、$\small 155x \equiv 1 \pmod {42}\quad \cdots ①$。

STEP

合同式の性質を使ってうまく「$\small x \equiv$〇$\small \pmod p$」の形をつくる

■合同式の性質
　・合同式同士は足し引きできるよ
　　$\small \color{red}a \equiv \color{red}b \pmod p$、$\small \color{blue}c \equiv \color{blue}d \pmod p$ならば、$\small \color{red}a \pm \color{blue}c \equiv \color{red}b \pm \color{blue}d \pmod p$

　・合同式の両辺は整数倍できるよ
　　$\small a \equiv b \pmod p$ならば $\small \color{red}ka \equiv \color{red}kb \pmod p$（$\small k$は0ではない整数）

　・合同式の両辺を割り算するときは互いに素を要チェック！
　　$\small k$と$\small p$が互いに素ならば、$\small \color{red}ka \equiv \color{red}kb \pmod p$のとき$\small a \equiv b \pmod p$

$\small 42x \equiv 0 \pmod{42}\quad \cdots②$（$\small 42x$は明らかに42の倍数なので42で割った余りは0）より、両辺を3倍すると$\small 126x \equiv 0 \pmod{42} \quad \cdots③$。

①-③より、

\begin{equation}
\begin{split}
155x-126x &\equiv 1-0 \pmod{42}\\
29x &\equiv 1 \pmod{42} \quad \cdots④\\
\end{split}
\end{equation}

②-④より

\begin{equation}
\begin{split}
42x-29x &\equiv 0-1 \pmod{42}\\
13x &\equiv -1 \pmod{42}\\
39x &\equiv -3 \pmod{42} \quad \cdots⑤\\
\end{split}
\end{equation}

⑤-④より

\begin{equation}
\begin{split}
39x-29x &\equiv -3-1 \pmod{42}\\
10x &\equiv -4 \pmod{42} \\
30x &\equiv -12 \pmod{42} \quad \cdots⑥\\
\end{split}
\end{equation}

⑥-④より

\begin{equation}
\begin{split}
30x-29x &\equiv -12-1 \pmod{42}\\
\color{red}x &\color{red}{\equiv -13 \pmod{42} }\\
\end{split}
\end{equation}

なんとか「$\small \color{red}{x \equiv \cdots}$」の形を作れました。この合同式を言語化すると「$\small x$は42で割ると-13余る数」ということなので、$\small \color{red}{x=42k-13}$（$\small k$は整数）が一般解だと求まります（特殊解を求めたつもりが一気に一般解まで求まっている！）。あとは、$\small x=42k-13$を問題文の方程式に代入することで$\small y$の一般解も$\small \color{red}{y=-155k+48}$と求めることができます。

【問題＆解説】不定方程式の演習問題

問題：不定方程式

方程式$\small 67x-60y=2$の整数解をすべて求めよ。

　解説

左辺が1ではないので、パターン2（$\small ax+by=c$型）の方針に従ってまずは、$\small 67x-60y=1$の特殊解を求める。自力で探すのは難しそうなので、簡易的互除法で特殊解を見つける（ユークリッドの互除法や合同式を使った解法はのちほど）。

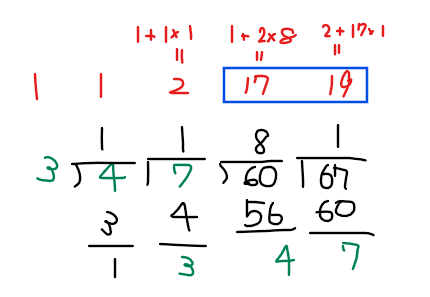
$\small 67 \times 17$の1の位は「9」、$\small 60 \times 19$の1の位は「0」なので「$\small \color{blue}{(60 \times 19)}-\color{red}{(67 \times 17)}$」とすれば、計算結果が1になる（1の位の計算は、0-9ではなく、10-9=1と考えるのがポイント）。

よって、

\begin{equation}
\begin{split}
60\cdot19-67\cdot17&=1\\
-67\cdot17+60\cdot19&=1\\
67\cdot(-17)-60\cdot(-19)&=1 \quad (67x-60y=1\mathbf{の形によせる})\\
\end{split}
\end{equation}

となり、$\small 67x-60y=1$と比較することで、仮の特殊解$\small (x,y)=(-17,-19)$が求まった。両辺を2倍することで

$$67\cdot(-34)-60\cdot(-38)=2$$

となることから、問題文の不定方程式 $\small 67x-60y=2$の特殊解は、$\small (x,y)=(-34,-38)$となる。

$\small 67x-60y=2$から$\small 67\cdot(-34)-60\cdot(-38)=2$を引き算することで

\begin{equation}
\begin{split}
67(x+34)-&60(y+38)=0\\
67(x+34)&=60(y+38)\quad \cdots①\\
\end{split}
\end{equation}

60と67は互いに素なので、$\small x+34=60k$（$\small k$は整数）、これを式①に代入することで

\begin{equation}
\begin{split}
67\cdot \color{red}{60k}&=60(y+38)\\
67k&=y+38\\
\end{split}
\end{equation}

よって、整数解は、$\small \color{red}{x=60k-34, \space y=67k-38}$。

（解答）
$\small \quad \color{red}{x=60k-34, \space y=67k-38}$（ただし、$\small k$は整数）

　別解1(ユークリッドの互除法)

ユークリッドの互除法の場合も、まずは$\small 67x-60y=1$の特殊解から求める。

\begin{equation}
\begin{split}
67&=60\cdot1+7→67-60\cdot1=7\cdots①\\
60&=7\cdot8+4\space\space →60-7\cdot8=4\cdots②\\
7&=4\cdot1+3\space\space →7-4\cdot1=3\cdots③\\
4&=3\cdot1+1\space\space →4-3\cdot1=1\cdots④\\
\end{split}
\end{equation}

④に③～①を順番に代入することで

\begin{equation}
\begin{split}
4-(7-4\cdot1)&=1\quad(\mathbf{③を代入})\\
-7+4\cdot2&=1\\
-7+(60-7\cdot8)\cdot2&=1\quad(\mathbf{②を代入})\\
60\cdot 2-7\cdot17&=1\\
60\cdot 2-(67-60\cdot1)\cdot17&=1\quad(\mathbf{①を代入})\\
-67\cdot17+60\cdot19&=1\\
67\cdot\color{blue}{(-17)}\color{red}-60\cdot\color{red}{(-19)}&=1\\
67\cdot\color{blue}{(-34)}-60\cdot\color{red}{(-38)}&=2\\
\end{split}
\end{equation}

よって、特殊解は$\small (x,y)=(-34,-38)$。以降の一般解の求め方は同じなので割愛。

　別解2(合同式)

$\small 67x-60y=1$の特殊解から考えてもよいが、合同式の場合は、$\small 67x-60y=2$の特殊解を直接求めることが可能。$\small x,y$の係数である67と-60のうち、絶対値が小さい60を法とした合同式を考える。

問題文から、$\small 67x=-60y+2$より、

$$67x \equiv 2 \pmod{60}\quad\cdots①$$

$\small 60x \equiv 0 \pmod{60}\cdots②$なので、①-②より、

\begin{equation}
\begin{split}
7x &\equiv 2 \pmod{60}\quad\cdots③\\
70x &\equiv 20 \pmod{60}\quad\cdots④\\
\end{split}
\end{equation}

④-①より

\begin{equation}
\begin{split}
3x &\equiv 18 \pmod{60}\\
6x &\equiv 36 \pmod{60}\quad\cdots⑤\\
\end{split}
\end{equation}

③-⑤より

$$x \equiv -34 \pmod{60}$$

よって、$\small x=60k-34$（$\small k$は整数）。$\small 67x+60y=2$に代入すると（頑張って計算…）

\begin{equation}
\begin{split}
67(60k-34)-60y&=2\\
67\cdot60k-2278-60y&=2\\
-60y=-67\cdot60k&+2280\\
y=67k&-38\\
\end{split}
\end{equation}

よって、、$\small \color{red}{x=60k-34,\space y=67k-38}$（$\small k$は整数）。

（補足）合同式は割り算に注意
途中式で$\small 3x \equiv 18 \pmod{60}$という結果が出てきたときに、全体を3で割って $\small x \equiv 6 \pmod{60}$としたくなりますが、これはNG。なぜなら、合同式の性質でも触れたように、modの$\small 60$と3は互いに素ではないため割ってはいけないのです。