【整数問題】3乗を含む不定方程式の整数解【有名大学入試の良問】【京大、千葉大、一橋大】

今回は、整数問題の王道、不定方程式の整数解を求める問題の中でも3乗を含んだ不定方程式について解説します。「整数解を求める問題の基礎は理解できたけど、実際の入試問題が解けない…」、「解き方や考え方のコツってあるの？」という人向けに、今回は京大、千葉大、一橋大の入試問題からセレクトした良問を用いながら分かりやすく解説していくので、ぜひ最後まで読んでみてください！

• 整数解を求める問題の入試問題を解くコツが知りたい！
• 以下のような不定方程式の整数問題が苦手…
  \(\small \color{red}{x^3-y^3=217}\) を満たす整数\(\small x,y\)の組を求めよ。
• いろいろな整数解を求める問題を解くことで自分の実力をアップさせたい！

本記事は、大学入試対策を想定しています。不定方程式の整数問題の基本を理解したいという人は、以下の記事から学習するのがよいかと思います！

★基本から学びたい人向け

• 【整数問題】不定方程式の整数解・自然数解（不等式絞り込みパターン）
• 【整数問題】不定方程式の整数解【2次式】（因数分解・判別式を用いた解き方）

【解説編】\(\small x^3 \pm y^3=k\)型の整数問題の解き方

3乗を含んだ不定方程式、\(\small x^3 \pm y^3=k\)型の整数解の求め方について解説します。初見で解くのはかなり大変ですが、今から説明するポイントを知っていれば、どんな問題でも解くことができますし、解の絞り込みも効率的にできるので、ぜひ覚えておきましょう！

不定方程式を文字と数字に分離して、因数分解して積の組み合わせパターンに持ち込む手法は王道ですが、数字が大きい場合、約数の組み合わせパターンが多くなり計算がかなり大変になるので解の絞り込みポイントはしっかり押さえておきたいですね。

では実際の問題を解きながら解説していきます。

【問題＆解説】\(\small x^3 \pm y^3=k\)型の整数解の問題

【問題1】\(\small k=\)(整数)の基本問題

問題の式は、\(\small (x-y)(x^2+xy +y^2)=7\cdot31\)と積の形に因数分解できる。ここで、

\begin{equation}
\begin{split}
x^2+xy +y^2&=\left(x+\frac{y}{2}\right)^2-\frac{y^2}{4}+y^2\\
&=\left(x+\frac{y}{2}\right)^2+\frac{3}{4}y^2\color{red}{≧0}\\
\end{split}
\end{equation}

より、\(\small (x-y)(x^2+xy +y^2)\)は\(\small x^2+xy +y^2\)が0以上なので、\(\small x-y\)も0以上が確定する。

（補足1）2乗の和≧0
実数を2乗すると必ず0以上になるので、それらの和も0以上（0以上同士のものを足しても0以上なので）になります。上式で何とかして括弧の2乗を作っているのも0以上になることを示すためです。整数問題でよく使う考え方なので身に着けておきましょう。

また、

\begin{equation}
\begin{split}
&(x^2+xy +y^2)-(x-y)\\
=&x^2+(y-1)x+y^2+y\\
=&\left(x+\frac{(y-1)}{2}\right)^2-\left(\frac{y-1}{2}\right)^2+y^2+y\\
=&\left(x+\frac{(y-1)}{2}\right)^2\color{red}{-\frac{y^2-2y+1}{4}}+\color{blue}{y^2+y}\\
=&\left(x+\frac{(y-1)}{2}\right)^2+\frac{\color{red}{-y^2+2y-1}+\color{blue}{4y^2+4y}}{4}\\
=&\left(x+\frac{(y-1)}{2}\right)^2+\frac{\color{red}{3y^2+6y}-1}{4}\\
=&\left(x+\frac{(y-1)}{2}\right)^2+\frac{\color{red}{3(y+1)^2-3}-1}{4}\\
=&\left(x+\frac{(y-1)}{2}\right)^2+\frac{3(y+1)^2}{4}-1\\
\color{red}{≧}&\color{red}{-1}\\
\end{split}
\end{equation}

より、\(\small x^2+xy +y^2\)と\(\small x-y\)の差は必ず-1以上になる。

（補足2）不等式評価について
上式の最後が-1以上になるのは、補足1の知識を使うと最終式が
\begin{equation}
\begin{split}
&\color{red}{\left(x+\frac{(y-1)}{2}\right)^2+\frac{3(y+1)^2}{4}}-1\\
&\color{red}{≧0}-1=-1
\end{split}
\end{equation}
と評価できるからである。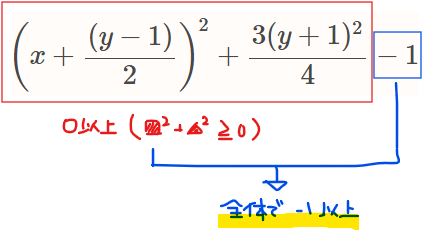

これら2つのことを考慮して積の組み合わせパターンを考えると

\begin{equation}
\begin{split}
&(x^2+xy +y^2,x-y)=(217,1)、(31,7)\\
\end{split}
\end{equation}

（補足3）積の組み合わせパターン
解答のように先に条件を確認しておいて解の組み合わせパターンを絞っておくと、洗い出しが楽になります。今回だと、\(\small (x^2+xy +y^2,x-y)=(-217,-1)、(-31,-7)\)などは、\(\small (x^2+xy +y^2,x-y)\)がともに0以上であること、\(\small (x^2+xy +y^2,x-y)=(1,217)、(7,31)\)などは、\(\small x^2+xy +y^2\)と\(\small x-y\)の差は必ず-1以上になることに反するので解として不適となる。
また、積の組み合わせを考えるときに、\(\small 7 \times 31\)の分けに気を取られて\(\small (217,1)\)の組を忘れないように注意しよう。一般に約数が\(\small n\)個ある場合、2数の整数解の組もn個（積が負であればその2倍）あるので抜け漏れチェックはしておこう。

[1]\(\small (x^2+xy +y^2,x-y)=(217,1)\)の場合

\(\small \color{blue}{x^2+xy +y^2}=\color{red}{(x-y)^2}+3xy\)より、左辺に\(\small \color{blue}{x^2+xy +y^2=217}\)、右辺に\(\small \color{red}{x-y=1}\)を代入することで、

\begin{equation}
\begin{split}
\color{blue}{217}&=\color{red}{1^2}+3xy\\
3xy&=216\\
xy&=72\
\end{split}
\end{equation}

\(\small x-y=1\space \Rightarrow x=y+1\)を\(\small xy=72\)に代入すると

\begin{equation}
\begin{split}
(y+1)y&=72\\
y^2+y-72&=0\\
(y+9)(y-8)&=0\\
\Rightarrow\space \color{red}{y=-9、}&\color{red}{8}\\
\end{split}
\end{equation}

よって、\(\small \color{red}{(x,y)=(-8、-9)、(9、8) \cdots ①}\)（\(\small x=y+1\)を用いた）

（補足）
もちろん、シンプルに\(\small x^2+xy +y^2=217\)に\(\small x=y+1\)をそのまま代入して\(\small y\)の2次方程式を解いてもよいが、少しでも計算を楽にする目的で上記のような式変形をしてます。

[2]\(\small (x^2+xy +y^2,x-y)=(31,7)\)の場合

[1]と同様、\(\small x^2+xy +y^2=(x-y)^2+3xy\)を用いると、

\begin{equation}
\begin{split}
31&=7^2+3xy\\
3xy&=-18\\
\color{red}xy&=-6\\
\color{red}{(y+7)}y&=-6\\
y^2+7y+6&=0\\
(y+1)(y+6)&=0\\
\Rightarrow\space \color{red}{y=-1、}&\color{red}{-6}\\
\end{split}
\end{equation}

よって、\(\small \color{red}{(x,y)=(6、-1)、(1、-6) \cdots ②}\).

よって、①、②をまとめたものが答え。

（解答）
\(\small \quad \color{red}{(x,y)=(-8、-9)、(9、8) 、(6、-1)、(1、-6) }\)

【問題2】\(\small k=\)(素数)の応用問題

\(\small (x+y)(x^2-xy+y^2)=p^2\)かつ \(\small \color{red}{x^2-xy+y^2≧0}\)より、\(\small x+y≧0\)が成り立つ。また、\(\small \color{red}{(x^2-xy+y^2)-(x+y)≧-1}\)より、\(\small (x^2-xy+y^2,x+y)=(p^2,1)、(p,p)\)に絞り込める。

（補足1）解の絞りこみ
\(\small (x^2-xy+y^2,x+y)=(1,p^2)\)は、\(\small p≧2\)（素数は2以上）であることから
\begin{equation}
\begin{split}
&(x^2-xy+y^2)-(x+y)\\
&=1-\color{red}{p^2}\\
&≦1-\color{red}{2^2}\\
&=-3\\
\end{split}
\end{equation}
なので、最大でも-3ということは-1以上にならないので不適。

さらに、\(\small x,y\)が自然数であることから、\(\small x+y≧2\)なので、\(\small (x^2-xy+y^2,x+y)=\color{red}{(p^2,1)}\)は解として不適。よって、\(\small (x^2-xy+y^2,x+y)=\color{red}{(p,p)}\)に確定する。

\(\small x^2-xy +y^2=(x+y)^2-3xy\)を用いると、

\begin{equation}
\begin{split}
p&=p^2-3xy\\
\Rightarrow \space 3xy&=p(p-1)\\
\end{split}
\end{equation}

\begin{cases}
3xy&=p(p-1)\\
x&=p-y\\
\end{cases}

を解くと、

\begin{equation}
\begin{split}
&3(p-y)y=p(p-1)\\
&3y^2-3py+p(p-1)=0\\
\end{split}
\end{equation}

上記を\(\small y\)の2次方程式とみなすと、\(\small y\)が整数解となるためには、少なくとも実数となる条件を満たす必要があるので、\(\small D≧0\)となる必要がある。

よって、
\begin{equation}
\begin{split}
D&=(-3p)^2-4\cdot 3\cdot p(p-1)≧0\\
\Rightarrow \space &9p^2-12p^2+12p≧0\\
\Rightarrow \space &-3p^2+12p≧0\\
\Rightarrow \space &p(p-4)≦0\\
\Rightarrow \space &0≦p≦4\\
\end{split}
\end{equation}

上記の範囲を満たす素数は\(\small p=2、3\)のみ。

[1] \(\small p=2\)の場合

\(\small 3y^2-3py+p(p-1)=0\)に代入すると

\begin{equation}
\begin{split}
3y^2-6y+2&=0\\
\Rightarrow \space y=\frac{3\pm \sqrt{3}}{3}
\end{split}
\end{equation}

となり、整数解ではないので不適。

[2] \(\small p=3\)の場合

\begin{equation}
\begin{split}
3y^2-9y+6&=0\\
3(y^2-3y+2)&=0\\
3(y-1)(y-2)&=0\\
\Rightarrow \space y=1、2
\end{split}
\end{equation}

\(\small x=3-y\)を用いて\(\small x\)の値を求めれば答えになる。

（解答）
\(\small \quad \color{red}{p=3、(x,y)=(2,1)、(1,2)}\)

【問題3】3乗を含む方程式の整数解（応用問題）

これまでとだいぶ見た目が異なりますが式の中に3乗が入ってますね。「\(\small m=10、n=1\)はすぐに見つけられたけど他にもあるのかな？」、「どこから手を付けよう…」と手が動かなくなりそうな問題ですが、少し式変形してあげるとこれまでの問題と同じように解くことができそうです。

\(\small m^3-n^3=10^3-1\)より、\(\small m^3-n^3=999\)を満たす整数\(\small m、n\)を求めることができればよい。

左辺は、\(\small (m-n)(m^2+mn+n^2)\)と因数分解でき、\(\small m^2+mn+n^2≧0\)であることから、\(\small \color{red}{m-n≧0 \cdots①}\)。また、\(\small \color{red}{m^2+mn+n^2-(m-n)≧-1 \cdots②}\)。

①、②を満たすことを考慮して\(\small (m-n)(m^2+mn+n^2)=999\)の積の組み合わせパターンを洗い出すと

\begin{equation}
\begin{split}
(m-n, m^2+mn+n^2)=&(1,999)、(3,333)、\\
&(9,111)、(27,37)\\
\end{split}
\end{equation}

さらに、\(\small m^2+mn+n^2=(m-n)^2+3mn\)なので、\(\small m^2+mn+n^2-(m-n)^2=\color{red}{3mn}\)、すなわち\(\small m^2+mn+n^2-(m-n)^2\)が3の倍数になる必要がある。

すると

\begin{split}
(m- & n, m^2+mn+n^2)\\
&=
\begin{cases}
(1,999)\mathbf{のとき}、999-1^2 \neq 3\mathbf{の倍数}\rightarrow \color{red}×\\
(3,333)\mathbf{のとき}、333-3^2 = 3\mathbf{の倍数}\rightarrow \color{red}〇\\
(9,111)\mathbf{のとき}、111-9^2 = 3\mathbf{の倍数}\rightarrow \color{red}〇\\
(27,37)\mathbf{のとき}、37-27^2 \neq 3\mathbf{の倍数}\rightarrow \color{red}×\\
\end{cases}
\end{split}

となるので、\(\small (m-n, m^2+mn+n^2)=(3,333)、(9,111)\)の2パターンに候補が絞れる。

（補足）3の倍数の見分け方
それぞれのパターンごとに計算して3の倍数かを確かめてもよいですが、「(3の倍数)-(3の倍数)=(3の倍数)」、「(3の倍数でない数)-(3の倍数)=(3の倍数ではない数)」（※引き算の順番は逆でも成り立つ）という性質を使うと計算せずに3の倍数かどうかを判別できるので楽です。
たとえば、上の例で、\(\small 333-3^2\)は\(\small 333\)は明らかに3の倍数ですし、\(\small 3^2\)も3が掛け算されただけなので3の倍数なので、引き算の結果も3の倍数と判断できます。
逆に、\(\small 37-27^2\)は37が3の倍数ではなく、\(\small 27^2\)が3の倍数なので、「(3の倍数でない数)-(3の倍数)=(3の倍数ではない数)」となります。

[1] \(\small (m-n, m^2+mn+n^2)=(3,333)\)の場合
\(\small 3mn=m^2+mn+n^2-(m-n)^2=333-3^2=324\)より\(\small mn=108\)。この式に、\(\small m=n+3\)を代入することで
\begin{split}
n(n+3)=&108\\
n^2+3n-108&=0\\
(n+12)(n-9)&=0\\
\Rightarrow \space n= -12& 、9\\
\end{split}
よって、\(\small (m,n)=(-9,-12)、(12,9)\cdots③\)

[2] \(\small (m-n, m^2+mn+n^2)=(9,111)\)の場合
同様に、\(\small 3mn=111-9^2=30\)より\(\small mn=10\)。この式に、\(\small m=n+9\)を代入することで
\begin{split}
n(n+9)=&10\\
n^2+9n-10&=0\\
(n-1)(n+10)&=0\\
\Rightarrow \space n= -10& 、1\\
\end{split}
よって、\(\small (m,n)=(-1,-10)、(10,1)\cdots④\)

③、④をまとめたものが答えになる。

（解答）
\(\small \quad \color{red}{(m,n)=(-9,-12)、(12,9)、(-1,-10)、(10,1)}\)

本記事のまとめ

今回は3乗を含む不定方程式の代表問題である\(\small x^3 \pm y^3 = k\)型の整数解の求め方を解説しました。整数問題はベースとなる考え方に加えて問題パターンごとの解き方を覚えておくことが重要になるので、今回のポイントもしっかり復習して解けるようにしておきましょう。

それでは今回はここまでです。お疲れさまでした！