【整数問題】不定方程式の整数解・自然数解（不等式絞り込みパターンの解き方）

今回は、方程式の整数解の求め方の基礎である不等式で解を絞り込むパターンの整数問題について解説していきます。「整数問題の解き方が全然わからない…」、「どう思考したら解答の解き方を思いつけるのか？」といった悩み、疑問を解決できる記事になっているので、ぜひ最後まで読んでみてください！

　本記事はこんな人におすすめ

不等式を使って整数解を絞り込むコツを知りたい！
どんな問題で不等式を使うのか知りたい！
問題を解いて自分の実力をチェックしたい！

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

【解き方解説】『方程式型』整数問題の解き方
1. 整数問題の基本パターン
2. 【苦手な人必見】自然数解を求める問題を解くコツ
【問題＆解説】方程式を満たす整数問題
本記事のまとめ

【解き方解説】『方程式型』整数問題の解き方

整数問題の基本パターン

方程式を題材とした整数問題には様々なパターンがありますが、今回は【まずはじめに押さえるべき】基本パターンを把握しておきましょう。

■方程式型整数問題の基本パターン
　・方程式の自然数解　☜ 今回はこっち
　　└$\small ax+by=c$ 型
　　└3つの文字を含む方程式
　　└分数型
　　└2次方程式型　etc…
　・方程式の整数解
　　└$\small kxy+\ell x+my+n=0$ 型
　　└分数型
　　└2次方程式型　etc…

【苦手な人必見】自然数解を求める問題を解くコツ

次は、前章で紹介した自然数解を求める問題の典型パターンの解き方について解説します。自然数解は整数解と異なり1以上の整数という制約があるので、この制約をうまく活用して解の候補を絞ることが問題を解くカギになります。

問題によって多少のカスタマイズはありますが、基本的には以下のポイントをおさえましょう！

■方程式の自然数解の求め方
　不等式で解の範囲を絞り込め！

・$\small ax+by=c$ 型の自然数解
　「不定方程式の解$\small ≧1$」で絞り込み

・3つの文字を含む方程式の自然数解
　文字をまとめて$\small ax+by=c$型の問題に帰着させろ！

・大小関係のある方程式の自然数解
　大きいもので置き換えて「問題の和≦★」の形で絞り込み

・2次方程式型の自然数解
　・判別式$\small D≧0$（実数解を持つ条件）
　・解の公式の「ルートの中身＝平方数」
　　で範囲を絞り込め！

では、実際の問題を解きながらそれぞれのポイントについて理解していきましょう。

【問題＆解説】方程式を満たす整数問題

【問題1】$\small ax+by=c$型の自然数解

問題1：$\small ax+by=c$ 型の自然数解

$\small 2x+5y=29$を満たす自然数$\small x,y$の組をすべて求めよ。

■$\small ax+by=c$ 型の自然数解
「不定方程式の解$\small ≧1$」で絞り込み

　解説

$\small x=2,y=5$が特殊解となっているので、

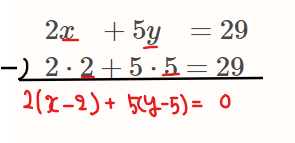
よって、

$$2(x-2)=-5(y-5)\quad \cdots①$$

2と5は互いに素なので、$\small x-2=5k$（$\small k$は整数）。これを①に代入して

\begin{equation}
\begin{split}
2\cdot(\color{red}{5k})&=-5(y-5)\\
2k&=-(y-5)\\
-2k&=y-5\\
y&=-2k+5\\
\end{split}
\end{equation}

よって、一般解は $\small x=5k+2,\space y=-2k+5\cdots②$となります。

（参考）不定方程式ってどうやって解くの？
不定方程式の解き方が怪しい人はこちらの記事で詳しく説明しているので、あわせて確認しておきましょう！
・【整数問題】ax+by=c型の不定方程式の解き方（ユークリッド互除法、合同式の利用）

ここで、今回の問題では$\small x,y$は自然数という条件があります。今の一般解では、例えば$\small k=3$であれば、$\small y$が負の値となっており自然数という条件に合致しません。そこで、求めた一般解に対して$\small x,y$が自然数となるように整数$\small k$の値の範囲を絞り込む必要があるわけです。

（補足）自然数ってなんだっけ？
自然数とは「$\small 1, 2, 3, \cdots$」のような1以上の正の整数です。「数を数えて！」って言われたら、普通「$\small 1, 2, 3, \cdots$」と数えていきますよね？なので「自然数」と言われています（「$\small \color{red}0,1, 2, \cdots$」」って数える人は少ないハズ！）。
もう少し話すと昔は「ゼロ」という概念がなかったんです。数字は数を数えるためにあったので物がない状態を数字で表すという発想がなかったわけです。なのでもともとの数字のことを指して自然数というわけです。

整数解 $\small x,y$が自然数になる条件は、$\small x≧1$ かつ $\small y≧1$（$\small x>0,y>0$としてもよいが、$\small x,y$は整数なので、1以上としても問題ない）なので、

\begin{equation}
\begin{cases}
x=5k+2≧1\space\mathbf{かつ}\\
y=-2k+5≧1\\
\end{cases}
\quad \cdots\mathbf{\color{blue}{\underline{今回のポイント}}}
\end{equation}

これらの不等式を解くと

\begin{cases}
k≧-\frac{1}{5}\space\mathbf{かつ}\\
k≦-2\\
\end{cases}

なので、共通範囲を求めると $\small -\dfrac{1}{5}≦k≦2$。この不等式を満たす整数$\small k$は、$\small k=0、1、2$の3つ。

（補足）共通範囲？合計範囲？
複数の不等式をすべて満たす範囲を「共通範囲」といいます。日本語では「かつ」と表現されます。旅行のホテル探しに例えるなら「夜景がきれいかつ食事がおいしいホテル」は、部屋から見える夜景がきれいじゃないといけないし宿の食事もおいしくなければいけません。
一方で、複数の不等式のうちどれか1つでも満たす範囲を「合計範囲」といいます。日本語では「または」と表現されます。旅行のホテル探しに例えるなら「夜景がきれいまたは食事がおいしいホテル」は、夜景がきれいじゃなくても食事がおいしければOK（またはその逆も可）で、必ずしもすべての条件を満たさなくてもよいという考え方です。

よって、それぞれの$\small k$の値を式②に代入することで、問題の方程式を満たす自然数$\small x,y$が求まります。

（解答）
$\small \quad \color{red}{(x,y)=(2,5)、(7,3)、(12,1)}$

【問題2】3つの文字を含む方程式の自然数解

問題2：3つの文字を含む方程式の自然数解

$\small x+3y+z=9$を満たす自然数$\small x,y,z$の組をすべて求めよ。

■3つの文字を含む方程式の自然数解
　文字をまとめて$\small ax+by=c$型の問題に帰着させろ！

　解説

$\small x+z=w$とおくことで問題の方程式は「 (1) $\small w+3y=9$を満たす自然数$\small w,y$の組を求める問題」と「(2) $\small x+z=w$を満たす自然数$\small x,z$を求める問題」の2つに分解することができます。では(1)から順番に解いていきましょう！

$\small w+3y=9$は$\small w=6,y=1$が特殊解なので、

\begin{equation}
\begin{split}
w+\space3y\space\space&=9\quad\cdots①\\
6+3\cdot1&=9\quad\cdots②\\
\end{split}
\end{equation}

①-②をすることで、$\small w-6+3(y-1)=0$、すなわち $\small \color{red}{w-6=-3(y-1)\cdots③}$。

③は右辺が3の倍数なので左辺も3の倍数になることから、$\small w-6=3k$（$\small k$は整数）より、$\small w=3k+6\cdots④$。この結果を式③に代入することで

\begin{equation}
\begin{split}
3k&=-3(y-1)\\
-k&=y-1\\
y&=-k+1\cdots⑤\\
\end{split}
\end{equation}

題意より$\small w,y$は自然数（$\small w$も$\small y$もどちらも自然数じゃないとダメなので（片方だけ自然数とかはだめ））なので、求める$\small k$の不等式の範囲は以下不等式の「共通範囲（かつ）」になります。

\begin{cases}
w=3k+6≧1\quad\mathbf{かつ}\\
y=-k+1≧1\\
\end{cases}

\begin{cases}
k≧-\dfrac{5}{3}\quad\mathbf{かつ}\\
k≦0\\
\end{cases}

よって、$\small \displaystyle -\frac{5}{3}≦k≦0$より、$\small k=-1,0$と求まります。あとは、この結果を式④、⑤に代入していけばOKです。

$\small k=-1$のとき、

\begin{cases}
w=3k+6=3\cdot\color{red}{(-1)}+6=\color{red}3\\
y=-k+1=-\cdot\color{red}{(-1)}+1=\color{red}2\\
\end{cases}

$\small w=3$と分かったので、冒頭の(2)の問題は、「$\small x+z=3$となる自然数$\small x,z$の組み合わせを求める問題」（$\small w=x+z$だったことを思い出そう）となり、それは$\small (x,z)=(1,2)、(2,1)$だけですね。

よって、$\small \color{red}{(x,y,z)=(1,2,2)、(2,2,1)\cdots⑥}$.

（補足）自然数の組み合わせを洗い出すコツ
一つの文字に着目して順番に大きくしていくと洗い出しやすいです。
上の問題であれば、$\small x$に着目して$\small x$を1、2と大きくしていき、$\small x=3$とすると、$\small z=0$となり自然数ではなくなるので、洗い出し完了になります（$\small x≧3$だと$\small z$が自然数じゃなくなることが計算するとすぐ分かります）。

$\small k=0$のときも同様に考えると

\begin{cases}
w=3k+6=3\cdot\color{red}0+6=\color{red}6\\
y=-k+1=-\cdot\color{red}{0}+1=\color{red}1\\
\end{cases}

なので、$\small x+z=6$を満たす自然数の組は$\small (x,z)=(1,5)、(2,4)、(3,3)、(4,2)、(5,1)$。よって、$\small \color{red}{(x,y,z)=(1,1,5)、(2,1,4)、(3,1,3)、(4,1,2)、(5,1,1)\cdots⑦}$。

⑥、⑦の組を合わせたものが答えになります。

（解答）
$\small \quad \color{red}{(x,y,z)=(1,1,5)、(2,1,4)、(3,1,3)、}$
$\small \qquad \qquad \color{red}{(4,1,2)、(5,1,1)、(1,2,2)、(2,2,1)}$

　別解

$$\small 3y=9-x-z≦9\color{red}{-1-1}=7$$

より、$\small 3y≦7$なので $\small y≦\dfrac{7}{3}$。$\small y$は自然数なので、この条件を満たすのは $\small \color{red}{y=1、2}$.

（補足）
$\small x,z$は自然数なので、$\small x≧1、z≧1$より $\small x+z≧2$（1以上のものと1以上のものを足したら2以上になる）.この式の両辺を-1倍して9を足すと
\begin{equation}
\begin{split}
\small \color{red}-(x+z)& \small ≦\color{red}-2\\
\small \color{red}9-(x+z)& \small ≦\color{red}9-2\\
\small \color{red}{9-x-z}&\color{red}{\small ≦7}\\
\end{split}
\end{equation}

（補足）なんで$\small y$の範囲を求めたの？
$\small x,y,z$の中で係数が一番大きいからです。$\small y$が1、2、3、…と大きくなるにつれて$\small 3y$はその3倍の3、6、9、…と大きくなるのですぐに全体和の9を超えます。$\small y$単独で全体和の9を超えてしまうと、$\small x、z$は自然数ですから満たす自然数解はなくなるのでその分素早くパターンを洗い出しやすいわけです。

$\small y=1$のとき、

\begin{equation}
\begin{split}
x+3y+z&=9\\
x+\color{red}3+z& =9\\
x+z& =6\\
\end{split}
\end{equation}

$\small y=2$のとき、

\begin{equation}
\begin{split}
x+3y+z&=9\\
x+\color{red}6+z& =9\\
x+z& =3\\
\end{split}
\end{equation}

となり、ここからの$\small x,z$の組み合わせの洗い出しは本線の解答と同じなので割愛。

（所感）
別解の方がたくさん文字を置かなくてよいので論証は楽かなと思い紹介しました。

【問題3】大小関係のある方程式の自然数解

問題3：大小関係のある自然数解

$\small \displaystyle \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$（$\small x≧y≧z$）を満たす自然数$\small x,y,z$の組をすべて求めよ。

■大小関係のある方程式の自然数解
　大きいもので置き換えて「問題の和≦★」の形で絞り込み

　解説

$\small x≧y≧z≧1$（自然数なので1以上）より、逆数の大小関係は

$$\color{red}{\frac{1}{x}≦\frac{1}{y}≦\frac{1}{z}≦1\quad \cdots①}$$

（補足）逆数の大小関係は逆転する
例えば、$\small 4≧2≧1$であれば、逆数の大小関係は $\small \displaystyle \frac{1}{4}≦\frac{1}{2}≦1$（$\small 0.25≦0.5≦1$）となりますね。

①より

\begin{equation}
\begin{split}
\color{red}{\frac{1}{x}+\frac{1}{y}}+\frac{1}{z}&≦\color{red}{\frac{1}{z}+\frac{1}{z}}+\frac{1}{z}=\frac{3}{z}\\
\Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z}&≦\frac{3}{z}\\
\end{split}
\end{equation}

（補足）
①の関係式を使って値が大きなものに置き換えることで「問題の和≦★」の形で不等式評価することができます。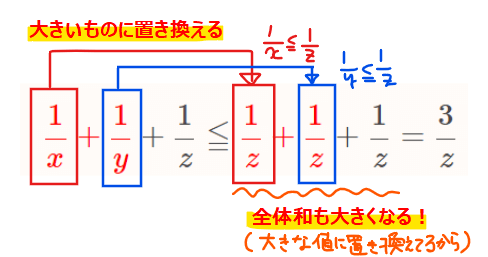

上記不等式の左辺は問題から$\small \displaystyle \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$なので、

\begin{equation}
\begin{split}
1&≦\frac{3}{z}\\
\Rightarrow z&≦3\space(z\mathbf{は自然数なので不等号の向きは変わらない})
\end{split}
\end{equation}

上記の不等式を満たす自然数 $\small z$は$\small z=1,2,3$。

[1] $\small z=1$のとき、問題の式は

\begin{equation}
\begin{split}
\frac{1}{x}+\frac{1}{y}+\color{red}1&=1\\
\frac{1}{x}+\frac{1}{y}&=0\\
\end{split}
\end{equation}

$\small \dfrac{1}{x}$ も $\small \dfrac{1}{y}$も0よりは大きな値なので、この2つを足した数はどうやっても0より大きくなるので上記の方程式を満たす$\small x、y$は存在しない。

（補足）$\small \displaystyle \frac{1}{x}+\frac{1}{y}=0$ の論証
自明なので解説で書いたような日本語的説明だけで済ませてしまっても減点にはならないはず。でも数式を使ってしっかり論証したいならば、以下のように示すとよいだろう。
$\small \displaystyle \frac{1}{x}+\frac{1}{y}=0$ の両辺を$\small xy$倍すると
\begin{equation}
\begin{split}
x+y&=0\\
\end{split}
\end{equation}
となるが、$\small x、y$は自然数より$\small x≧1、y≧1$なので $\small x+y≧2$となる。よって、$\small x+y=0$はこの条件を満たさないため解は存在しない。

[2] $\small z=2$のとき、問題文の式は

\begin{equation}
\begin{split}
\frac{1}{x}+\frac{1}{y}+\frac{1}{\color{red}2}&=1\\
\frac{1}{x}+\frac{1}{y}&=\frac{1}{2}\cdots②\\
\end{split}
\end{equation}

ここで①の関係式より

\begin{equation}
\begin{split}
\color{red}{\frac{1}{x}}+\frac{1}{y}&≦\color{red}{\frac{1}{y}}+\frac{1}{y}=\frac{2}{y}\\
\frac{1}{x}+\frac{1}{y}&≦\frac{2}{y}\\
\end{split}
\end{equation}

左辺に式②を代入すると

\begin{equation}
\begin{split}
\frac{1}{2}&≦\frac{2}{y}\\
y&≦4\\
\end{split}
\end{equation}

ここで、問題文の条件 $\small x≧y≧z$より、$\small x≧y≧\color{red}2$なので、$\small 2≦y≦4$となり$\small \color{red}{y=2、3、4}$。これをそれぞれ計算すると以下の通り。

$\small y=2$を式②に代入すると、$\small \displaystyle \frac{1}{x}+\frac{1}{\color{red}2}=\frac{1}{2}$ → $\small \displaystyle \frac{1}{x}=0$となりこの式を満たす自然数$\small x$は存在しない。

$\small y=3$を式②に代入すると、$\small \displaystyle \frac{1}{x}+\frac{1}{\color{red}3}=\frac{1}{2}$ → $\small \displaystyle \frac{1}{x}=\frac{1}{6}$となりこの式を満たす自然数$\small x$は$\small x=6$。

$\small y=4$を式②に代入すると、$\small \displaystyle \frac{1}{x}+\frac{1}{\color{red}4}=\frac{1}{2}$ → $\small \displaystyle \frac{1}{x}=\frac{1}{4}$となりこの式を満たす自然数$\small x$は$\small x=4$。

[3] $\small z=3$のとき、問題文の式は

\begin{equation}
\begin{split}
\frac{1}{x}+\frac{1}{y}+\frac{1}{\color{red}3}&=1\\
\frac{1}{x}+\frac{1}{y}&=\frac{2}{3}\cdots③\\
\end{split}
\end{equation}

ここで[2]同様に

\begin{equation}
\begin{split}
\color{red}{\frac{1}{x}}+\frac{1}{y}&≦\color{red}{\frac{1}{y}}+\frac{1}{y}=\frac{2}{y}\\
\frac{1}{x}+\frac{1}{y}&≦\frac{2}{y}\\
\end{split}
\end{equation}

なので、上記左辺に③を代入することで

\begin{equation}
\begin{split}
\frac{2}{3}&≦\frac{2}{y}\\
y&≦3\\
\end{split}
\end{equation}

問題文の条件 $\small x≧y≧z$より、$\small x≧y≧\color{red}3$なので、$\small 3≦y≦3$となり$\small \color{red}{y=3}$。式③に代入することで、$\small \displaystyle \frac{1}{x}+\frac{1}{\color{red}3}=\frac{2}{3}$ → $\small \displaystyle \frac{1}{x}=\frac{1}{3}$となりこの式を満たす自然数$\small x$は$\small x=3$となります。

以上の結果を頑張って整理すると答えになります。（解答との対応関係が分かりやすいように問題で見つけた順に答えを記載してます↓）

（解答）
$\small \quad \color{red}{(x,y,z)=(6,3,2)、(4,4,2)、(3,3,3)}$

【問題4】2次方程式型の自然数解

問題4：2次方程式型の自然数解

$\small x^2+2xy+3y^2=27$を満たす自然数$\small x,y$の組をすべて求めよ。

■2次方程式型の自然数解
　・判別式$\small D≧0$（実数解を持つ条件）
　・解の公式の「ルートの中身＝平方数」
　　で範囲を絞り込め！

　解説

$\small x^2+2xy+3y^2=27$を$\small x$に関する2次方程式と捉えると

$$\color{red}{x^2}+(2y)\color{red}x+(3y^2-27)=0\cdots①$$

と整理できる。$\small x$が自然数解となるとき、上記の2次方程式は少なくとも実数解を持つ必要があるので

\begin{equation}
\begin{split}
\frac{D}{4}=&y^2-1\cdot(3y^2-27)\color{red}{≧0}\\
\Rightarrow \space&-2y^2 ≧-27\\
\Rightarrow \space& y^2 ≦\frac{27}{2}=13.5\\
\end{split}
\end{equation}

よって、この不等式を満たす自然数$\small y$は$\small y=1、2、3$（$\small y=4$だと$\small y^2=16>13.5$となり不適）。

（補足）少なくとも実数解を持つ
「少なくとも」と書いたのは、実数解を持てば必ず自然数というわけではないから。実数とは、負の数や分数、無理数なども含むので自然数よりもかなり緩めの条件ですが、値の絞り込みという観点では有効なのでどんどん活用しましょう。

さらに、式①の解は2次方程式の解の公式から

\begin{equation}
\begin{split}
x&=-y \pm \sqrt{y^2-1\cdot(3y^2-27)}\\
&=-y \pm \sqrt{-2y^2+27}\cdots②\\
\end{split}
\end{equation}

なので、$\small x$が自然数になるには少なくともルートの中身 $\small -2y^2+27$が平方数（$\small \color{red}{★^2}$）になっている必要があることも考慮すると

\begin{cases}
y=1\mathbf{ のとき、}-2y^2+27=25\space→〇\\
y=2\mathbf{ のとき、}-2y^2+27=19\space→\color{red}{×(\mathbf{平方数じゃない})}\\
y=3\mathbf{ のとき、}-2y^2+27=9\space→〇\\
\end{cases}

よって、$\small y=1、3$だけ考えればよい。

[1] $\small y=1$のとき、②は $\small x=-1 \pm \sqrt{25}=-1\pm 5=4,-6$。$\small x$は自然数なので、$\small \color{red}{x=4}$。

[2] $\small y=3$のとき、②は $\small x=-3 \pm \sqrt{9}=-3\pm 3=0,-6$。どちらも自然数ではないので不適。

（解答）
$\small \quad \color{red}{(x,y)=(4,1)}$