【整数問題】不定方程式の整数解【2次式】（因数分解・判別式を用いた解き方）

今回は、2次不定方程式の整数解の問題を解説します。「整数解を求めるのが苦手…」、「どうやって解いていけばいいのか分からない…」という悩みを抱えている人向けに、2次不定方程式の解き方のポイントと実際の問題を解く際の思考回路を整理しているので、ぜひ最後まで読んでみてください！

• 2次不定方程式の解き方が知りたい！
• 問題を解く方針をどう見極めればいいのか知りたい！
• 問題を解いて自分の実力をチェックしたい！

【解き方解説】2次不定方程式の整数解の求め方

整数問題の基本パターン

整数問題の典型パターンである不定方程式の整数解を求める問題には大きく2種類のパターンがあります。それが「方程式の自然数解を求める問題」と「方程式の整数解を求める問題」です。

前者の「自然数解」を求める方法については、「【整数問題】不定方程式の整数解・自然数解（不等式絞り込みパターン）」の記事で解説したので、今回は少し難易度アップした「整数解」を求める方法に詳しく解説していきます。

■方程式型整数問題の基本パターン
　・方程式の自然数解
　　└\(\small ax+by=c\) 型
　　└3つの文字を含む方程式
　　└分数型
　　└2次方程式型　etc…
　・方程式の整数解　☜ 今回はこっち
　　└\(\small kxy+\ell x+my+n=0\) 型
　　└分数型
　　└2次方程式型　etc…

【苦手な人必見】整数解を求める問題を解くコツ

整数解を求める問題が自然数解を求める問題と圧倒的に異なるのが「解の絞り込みのアプローチ」です。

自然数解のときは、「求める解≧1」という条件を突破口に解の範囲を絞り込んできました。一方で整数解になると解の候補がマイナスの範囲まで広がるため、うまく条件を絞ることができません。やみくもに探しても答えの範囲が広すぎて見つけるだけでも一苦労ですし、漏れなく探せているかの確認もできないです…。

じゃあ、何か突破口はないのか？実は、整数解を求める問題はほぼほぼ2次式のことが多いので、2次方程式の性質をうまく利用します。2次方程式の解を求めるときにでてくる「因数分解する」、「解の公式（判別式）を使う」という考え方を活用して問題を解くことができます。

では実際の問題を解きながらポイントを理解していきましょう。

【問題＆解説】2次不定方程式の整数問題

【問題1】\(\small kxy+\ell x+my+n=0\) 型の整数解

（補足）2次不定方程式とは？
2次式の不定方程式のこと。2次式とは、\(\small x^2\)や\(\small xy\)など一つの項に文字が2つかけ算されたものが含まれている方程式のことです。\(\small kxy+\ell x+my+n=0\) は2乗がないので1次式と思われがちですが、\(\small xy\)という項が含まれるので2次式になります。

\(\small xy+3x+2y+5=0\)を因数分解すると

\begin{equation}
\begin{split}
xy+3x+2y+5\color{red}{+1}&=\color{red}1\\
(x+2)(y+3)&=1\\
\end{split}
\end{equation}

\(\small x、y\)は整数なので、\(\small x+2、y+3\)ももちろん整数より、かけ算して1になる組み合わせは、

\begin{cases}
\color{red}{1 \times 1} &= 1\\
\color{red}{(-1) \times (-1)} &= 1\\
\end{cases}

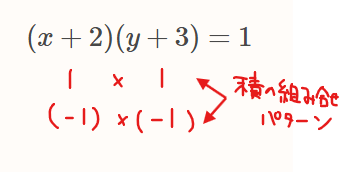
の2パターンのみ。よって、\(\small (x+2,y+3)=(1,1)、(-1,-1)\)を\(\small x、y\)について解けば答えになる。

（解答）
\(\small \quad \color{red}{(x,y)=(-1,-2)、(-3,-4)}\)

【問題2】分数型の整数解

分数の分母は0にならないことから、\(\small \color{red}{x \neq 0、y \neq 0 \cdots①}\).

問題文の式の両辺を \(\small xy\)倍して整理すると

\begin{equation}
\begin{split}
\color{red}{xy}\left( \frac{1}{x}+\frac{2}{y}+\frac{3}{xy}\right)&=\color{red}{xy}\cdot1\\
y+2x+3&=xy\\
xy-2x-y-3&=0\\
xy-2x-y-3\color{red}{+5}&=\color{red}5\\
(x-1)(y-2)&=5\\
\end{split}
\end{equation}

\(\small x、y\)は整数なので\(\small x-1、y-2\)も整数であることから、上式を満たす積の組み合わせパターンは、

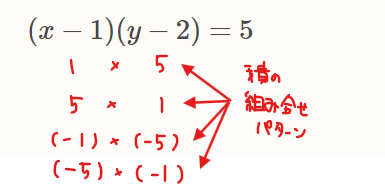
の計4つ。このときの \(\small x、y\)の組み合わせは

\begin{equation}
\begin{split}
(x-1,y-2)&=(1,5)、(5,1)、(-1,-5)、(-5,-1)\\
\Rightarrow \quad (x,y)&=(2,7)、(6,3)、(0,-3)、(-4,1)
\end{split}
\end{equation}

このうち、①の条件 \(\small \color{red}{x \neq 0、y \neq 0 }\)を考慮すると、\(\small (0,-3)\)は解として不適であることに気を付ける.

（解答）
\(\small \quad \color{red}{ (x,y)=(2,7)、(6,3)、(-4,1)}\)

【問題3】2次方程式型の整数解（判別式の利用）

問題の式を\(\small x\)に関する2次方程式とみなして整理すると

$$\color{red}{x^2}−2\color{red}x+(4y^2−4y−23)=0$$

上記方程式の解が整数解になるということは、少なくとも判別式\(\small D/4≧0\)（実数解）となる必要があるので

\begin{equation}
\begin{split}
\frac{D}{4}=(-1)^2-1\cdot(4y^2−4y−23)&≧0\\
-4y^2+4y+24&≧0\\
-4(y^2−y−6)&≧0\\
(y+2)(y-3)&≦0\\
\Rightarrow \space \color{red}{-2≦y≦3}&\\
\end{split}
\end{equation}

よって、\(\small y\)の候補は、\(\small \color{red}{y=-2、-1、0、1、2、3}\)に絞れました。あとは、それぞれの\(\small y\) の値を問題の式に代入して\(\small x\) が整数解になるかどうかを確認していけばよいのですが、若干数が多いのでもう少し絞れないか考えます。

2次方程式の \(\small x\)の解は解の公式より

\begin{equation}
\begin{split}
x&=1\pm\sqrt{-4(y+2)(y-3)}\\
&=1\pm 2\sqrt{\color{red}{-(y+2)(y-3)}}\cdots①\\
\end{split}
\end{equation}

ここで、\(\small x\)が整数解になるためにはルートの中身（赤色部分）が平方数になっている必要があります。なので、それぞれの\(\small y\)の値で赤色箇所が2乗の形になるかを確認していきます。

（補足）\(\small \sqrt{-(y+2)(y-3)}\)ってルートの中身がマイナスになるの？
\(\small y\)の値によってはマイナスになります。その場合は実数解なしとなりますが、判別式\(\small D≧0\)の条件から\(\small y\)の値を出しているので、今回はどの値を代入してもルートの中身は0以上になります。
※数式上はマイナスがついているが \(\small y-3≦0\)なので先頭のマイナスと打ち消し合って全体としては0以上になります（\(\small \sqrt{(y+2)(3-y)}\)ということ）

\begin{equation}
\color{red}{-(y+2)(y-3)}=
\begin{cases}
\color{red}{y=-2 \mathbf{のとき、}0\space\rightarrow〇}\\
\color{red}{y=-1 \mathbf{のとき、}4\space\rightarrow〇}\\
y=0 \mathbf{のとき、}6\space\rightarrow×\\
y=1 \mathbf{のとき、}6\space\rightarrow×\\
\color{red}{y=2 \mathbf{のとき、}4\space\rightarrow〇}\\
\color{red}{y=3 \mathbf{のとき、}0\space\rightarrow〇}\\
\end{cases}
\end{equation}

よって、上記赤字の4パターンを考えれば答えになります。

[1] \(\small y=-2\) のとき、式①に代入して \(\small x=1\)

[2] \(\small y=-1\) のとき、式①に代入して \(\small x=1\pm 4=\color{red}{5、-3}\)。どちらも整数なので解の条件を満たす。

[3] \(\small y=2\) のとき、式①に代入して \(\small x=1\pm 4=\color{red}{5、-3}\)。どちらも整数なので解の条件を満たす。

[4] \(\small y=3\) のとき、式①に代入して \(\small x=1\)

よって、[1]～[4]の解の組み合わせを整理したものが答え.

（解答）
\(\small \quad \color{red}{(x,y)=(1,-2)、(5,-1)、(-3,-1)、(5,2)、(-3,2)、(1,3)}\)

【問題4】2次方程式型の整数解（因数分解の利用）

\(\small x\)に関する2次方程式とみなすと

$$x^2-(y-3)x-(2y^2-3y+1)＝0$$

上記の2次方程式の解が少なくとも実数解となる必要があることから

\begin{equation}
\begin{split}
D=(y-3)^2-4\cdot1\cdot\{-(2y^2-3y+1)\}&≧0\\
(y^2-6y+9)+8y^2+12y+4&≧0\\
\color{red}{9y^2+6y}+13&≧0\\
\color{red}{9 \left( y^2+\frac{2}{3}y \right)}+13&≧0\\
\color{red}{9 \left( y^2+\frac{2}{3}y \color{blue}{+\frac{1}{9}}\right)\color{blue}{-1}}+13&≧0\\
\color{red}{9 \left( y+\frac{1}{3}\right)^2}+12&≧0\\
\end{split}
\end{equation}

上式の左辺は「\(\small \color{red}{(\mathbf{数字})^2+12}\)」なので、\(\small y\)の値にかかわらず必ず0以上となるため、判別式では\(\small y\)の値の範囲を絞り込むことができない。

（補足）
\(\small 9y^2+6y+13\)は\(\small y\)の値によらずに常に正であるということを論証するために、平方完成して「\(\small (\mathbf{●})^2+\mathbf{■}≧0\)」を示している。\(\small 3^2=9、(-2)^2=4\)のように2乗する数がどんな数であっても2乗してしまえば0以上になるのでそこに正の数を足しても0以上は変わらない。
他にも、不等式が常に成り立つ条件として、\(\small 9y^2+6y+13\)の判別式が負になることを示してもよい。

今回の場合は判別式では解の範囲を絞れないので、因数分解で解く方法で検討する。

ここで左辺は

\begin{equation}
\begin{split}
&x^2-(y-3)x-\color{red}{(2y^2-3y+1)}\\
&x^2-(y-3)x-\color{red}{(2y-1)(y-1)}\\
\end{split}
\end{equation}

と因数分解できるので、\(\small x\)の2次方程式全体をたすき掛けを使って因数分解をしようとすると

となり、\(\small x\)の係数である\(\small \color{blue}{-y+3}\)と若干ずれる。この部分の帳尻を合わせるためには、\(\small (2y\color{blue}{-1})(y\color{blue}{-1})\)の定数部分（青字）で調整するしかないので、青字部分を\(\small a,b\)と文字で置いた\(\small x^2-(y-3)x-\color{blue}{(2y+a)(y+b)}\)を考える。

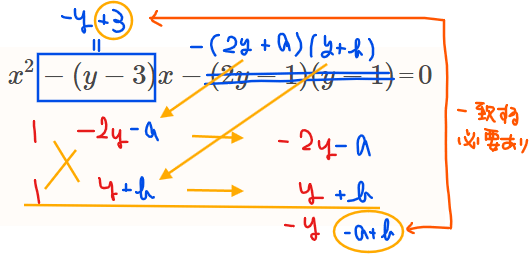
このとき、\(\small x\)の係数が\(\small -y+3\)になればよいので、

$$-a+b=3\quad \cdots ①$$

また、\(\small x^2-(y-3)x-\color{blue}{(2y+a)(y+b)}\)を展開すると

$$x^2-(y-3)x-\{ \color{blue}{2y^2+(a+2b)y+ab}\}$$

となるので、青字箇所の\(\small y\)の係数をもとの式と比較することで

$$a+2b=-3 \quad \cdots②$$

①、②を連立させることで、\(\small a=-3、b=0\)を得る。

（補足）\(\small ab=1\)はダメなのか？
定数項を合わせにいくと
\begin{cases}
-a+b&=3\\
ab&=1\\
\end{cases}
となり、\(\small a、b\)がルートを含んだ解になるため、整数問題を考える上では面倒になる。きれいな整数になるようにするには、\(\small y\)の係数の方を合わせにいき、定数項はあとで帳尻合わせするのがよいだろう。

\(\small x^2-(y-3)x-(2y+a)(y+b)\)に\(\small a=-3、b=0\)を代入して因数分解すると

\begin{equation}
\begin{split}
&x^2-(y-3)x-(2y\color{red}{-3})(y+\color{red}0)\\
\Rightarrow \space &x^2-(y-3)x-(2y-3)y\\
\end{split}
\end{equation}

$$\Rightarrow \space \color{red}{(x-2y+3)(x+y)}\quad \cdots③$$

一方でこの式を展開すると

\begin{equation}
\begin{split}
&x^2-(y-3)x-(2y-3)y\\
\Rightarrow \space &x^2-(y-3)x-2y^2+3y\\
\end{split}
\end{equation}

となり、もともとの式 \(\small x^2-(y-3)x-(2y^2-3y+1)＝0\)と比較すると

\begin{equation}
\begin{split}
x^2-(y-3)x-(2y^2-3y+1) &＝0\\
\Rightarrow \space \color{red}{x^2-(y-3)x-2y^2+3y} -1 &＝0\\
\Rightarrow \space \color{red}{x^2-(y-3)x-2y^2+3y}&＝1\\
\end{split}
\end{equation}

上記左辺は③のように因数分解できるので

$$\color{red}{(x-2y+3)(x+y)}＝1$$

\(\small x、y\)が整数解のとき、\(\small x-2y+3、x+y\)はどちらも整数になるので、上式を満たす組み合わせは、

$$(x-2y+3,x+y)=(1,1)、(-1,-1)$$

それぞれ、以下の連立方程式を解くことで\(\small x、y\)の値を求めることができる。

\begin{equation}
\begin{cases}
x-2y+3&=1\\
x+y&=1\\
\end{cases}
\space \Rightarrow \space \color{red}{(x,y)=(0,1)}
\end{equation}

\begin{equation}
\begin{cases}
x-2y+3&=-1\\
x+y&=-1\\
\end{cases}
\space \Rightarrow \space \color{red}{(x,y)=(-2,1)}
\end{equation}

（解答）
\(\small \quad \color{red}{(x,y)=(0,1)、(-2,1)}\)

（補足）
多くの問題では2次方程式を因数分解して解く場合、設問1が因数分解の誘導問題になっていることがほとんどです。誘導がついていないときには、解説で示したように因数分解の形から逆算して、定数項をうまく帳尻合わせしましょう。

【問題5】2次方程式型の整数解（\(\small (\)実数\(\small )^2\)の活用）

\begin{equation}
\begin{split}
x^2+2xy+2y^2&＝1\\
\color{red}{x^2+2xy+y^2}+y^2&＝1\\
\color{red}{(x+y)^2}+y^2&＝1\\
(x+y)^2＝1-y^2&\color{red}{≧0}\\
\end{split}
\end{equation}

より、\(\small y^2≦1\)なので、\(\small y=-1、0、1\)と解の候補を絞り込むことができる。あとはそれぞれの\(\small y\)の値をもとの式に代入して\(\small x\)が整数解になるかを確認してもよいが、小技として途中式の\(\small (x+y)^2+y^2＝1\)に代入すると計算がしやすい。

\begin{equation}
\begin{cases}
y=-1\mathbf{のとき、} &(x-1)^2=0\\
&\Rightarrow \space x=1\\
y=0\mathbf{のとき、} &x^2=1\\
&\Rightarrow \space x=\pm1\\
y=1\mathbf{のとき、} &(x+1)^2=0\\
&\Rightarrow \space x=-1\\
\end{cases}
\end{equation}

この結果を整理すれば答えになる。

（解答）
\(\small \quad \color{red}{(x,y)=(1,-1)、(-1,0)、(1,0)、(-1,1)}\)

【補足説明】結局、2次方程式型はどう解けばいい？

あえて最後に問題5を紹介したのは、よく参考書で\(\small (\)実数\(\small )^2\)を作ることで解の候補を絞り込む方法が解説されているからです。でも、そこでこんな疑問が生まれます。「\(\small (\)実数\(\small )^2\)を作る解法を使う場合と判別式で解く場合、因数分解で解く場合ってどう見分ければいいのか？」。ここではその答えについて解説をします。

結論、判別式→因数分解の順番で考えていけばOKです。あれ？実数の2乗はどうした？と思ったかもしれませんが、個人的には、実数の2乗で解く方法は考えなくていいかなと思っています。理由は、判別式を使えば解けるからです。

実際に問題5を判別式を使って解くと以下の通りです。

問題の式を\(\small x\)の2次方程式とみなすと
$$x^2+2yx+(2y^2-1)=0$$
方程式の解は少なくとも実数である必要があることから、判別式 \(\small \displaystyle \frac{D}{4}≧0\)を考えると
\begin{equation}
\begin{split}
\frac{D}{4}=1^2-1\cdot (2y^2-1)&≧0\\
-2y^2+2&≧0\\
y^2&≦1\\
\Rightarrow \space \color{red}{-1≦y}&\color{red}{≦1}\\
\end{split}
\end{equation}
となり、整数解の候補を\(\small y=-1、0、1\)に絞り込むことができる（以降同様のため略）.

2次方程式型の整数解の求め方のポイントにも「判別式での解法【パターン1】」と「因数分解での解法【パターン2】」しか書いてない意図はそういうことです。

じゃあ、なんで参考書には実数の2乗の解法が紹介されているのか？それは、実数の2乗で解けるならその方が楽に解けるからです。個人的には、まずは問題が解けるようになることが大事で、そのための解法パターンはなるべく少ない方が迷わなくていいと思っています。そして、整数問題に慣れてきたら、より簡単に解ける解法や小手先のテクニックを覚えていくのがよいでしょう。

本記事のまとめ

今回は、2次不定方程式の整数解を求める問題の解き方についてパターン別に解説してみました。問題のパターンとそれぞれの解き方は以下の通りです。

ここにある問題が解ければ基礎固めはばっちりでしょう。より実践的な問題にも取り組んでいけると思うので、ぜひ頑張って整数問題の苦手を克服していきましょう。

それでは今回はここまでです。お疲れさまでした！