【数Ⅲ】媒介変数表示された曲線の面積計算（積分の応用問題を徹底解説）

#PCやタブレットなどの大画面でご覧いただくと数式などが見やすいくなりおすすめです！

今回は媒介変数表示された曲線の面積を求める問題を解説します。媒介変数表示で表される曲線は、グラフの概形把握や積分計算も大変なことが多く苦手意識を持つ人が多い分野だと思います。

そこで本記事では、媒介変数表示を含む曲線の面積を求めるコツや考え方について分かりやすく解説していきますので、一緒に理解を深めていきましょう！

　本記事はこんな人におすすめ

媒介変数表示された関数の面積を求める問題に挑戦したい人
大学入試を用いた問題演習がしたい人
定期テスト対策がしたい人

　本記事のレベル

重要度

低

余力あれば

普通

必須

高
難易度

易しい

易

やや易

やや難

難

難しい
暗記/理解

暗記重視

暗記

半々

理解

理解重視

【問題＆解説】媒介変数表示を含む関数の積分計算
1. 【問題1】媒介変数表示された曲線と面積（場合分けなし）（難易度：★★☆）
2. 【問題2】媒介変数表示された曲線と面積（場合分けあり）（難易度：★★☆）
本記事のまとめ

【問題＆解説】媒介変数表示を含む関数の積分計算

【問題1】媒介変数表示された曲線と面積（場合分けなし）（難易度：★★☆）

直線$\small \ell:2x-\sqrt{3}y=0$と、媒介変数で表された曲線$\small \displaystyle C:x=\tan t, \space y=\frac{1}{\cos t}\space \left(0≦t <\frac{\pi}{2}\right)$を考える。
（1）$\small \ell$と$\small C$の交点の座標を求めよ。
（2）$\small \ell$と$\small C$および$\small y$軸で囲まれた部分の面積を求めよ。 [東北大]

問題解決のKey

・（1）は交点の座標なので、直線$\small \ell $と曲線$\small C$の方程式を連立して得られる三角関数の方程式を条件 $\small \displaystyle 0≦t < \frac{\pi}{2}$の範囲で解けばよい。
・一般的に定義域 $\small a≦x≦b$の範囲で関数$\small y=f(x)$と$\small x$軸で囲まれた面積は
\begin{split}
\small S &\small =\color{red}{\int_a^b y dx}\\
&\small =\int_a^b f(x)dx \\
\end{split}
が成り立つ。媒介変数を含む関数の面積を求める問題では、上記の1行目の公式を媒介変数$\small t$の積分に置き換える方針で考えると分かりやすい。
ちなみに、面積を求める式がなぜ1行目の計算で求まるのかを簡単に説明しておくと、微小な長方形の面積$\small y\times dx$を$\small a≦x≦b$の範囲で積み上げたものが求める面積になるからだ。

　解説（1）

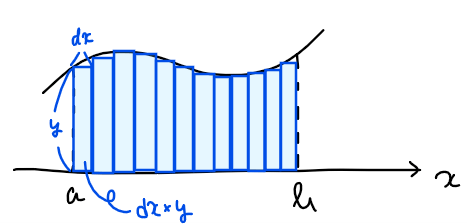
直線 $\small \ell$と曲線 $\small C$の交点を求めるには、

\begin{cases}
\small \ell:2x-\sqrt{3}y=0 \space \cdots①\\
\small \displaystyle C:x=\tan t, \space y=\frac{1}{\cos t} \space \cdots②\\
\end{cases}

の2式を連立すればよい。

②を①に代入することで、

\begin{split}
&\small \displaystyle 2\tan t-\frac{\sqrt{3}}{\cos t}=0\\
&\small \displaystyle \frac{2\sin t}{\cos t}-\frac{\sqrt{3}}{\cos t}=0\\
&\small \displaystyle ∴\space \sin t=\frac{\sqrt{3}}{2}\\
\end{split}

この方程式を、$\small \displaystyle 0≦t <\frac{\pi}{2}$の範囲で解くと

\begin{split}
&\small \displaystyle t=\frac{\pi}{3}\\
\end{split}

よって、直線 $\small \ell$と曲線 $\small C$の交点は、$\small \displaystyle t=\frac{\pi}{3}$のときであることが分かったので、②に代入することで交点の$\small x,y$座標は、

\begin{cases}
\small \displaystyle x=\tan\left(\frac{\pi}{3}\right)=\sqrt{3}\\
\small \displaystyle y=\frac{1}{\cos \left(\dfrac{\pi}{3}\right)}=2 \\
\end{cases}

よって、交点の座標は、$\small (\sqrt{3},2)$…【答】.

　解説（2）

曲線$\small C$のグラフの概形まで厳密に調べなくても、（1）で直線$\small \ell$との交点は1つのみであることが分かっているので、求める面積の概形をおおよそ把握することができる（下図赤線）。

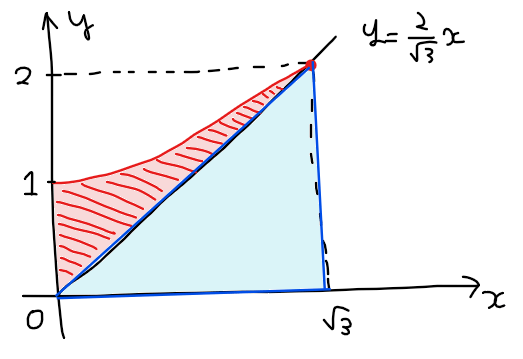
●補足
領域の面積を計算するうえで重要なのは、曲線$\small C$と直線$\small \ell$と$\small y$軸の位置関係であり、赤線で示す曲線$\small C$が上図のような概形なのか下図のような概形なのかによって、求める面積の計算式は変わらないので、解答を記載するときもそこまで厳密なグラフの概形を計算する必要はない。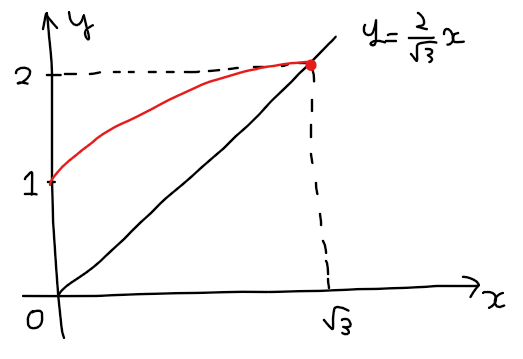

グラフの概形は、②より$\small t=0$のときの座標が$\small (0,1)$、$\small \displaystyle t=\frac{\pi}{2}$のときの座標が$\small x\to+\infty,\space y\to+\infty$（$\small xy$平面の右上方向）で、点$\small (\sqrt{3},2)$で直線$\small \ell$と交わるということさえ押さえていれば、ある程度の概形は把握できるだろう。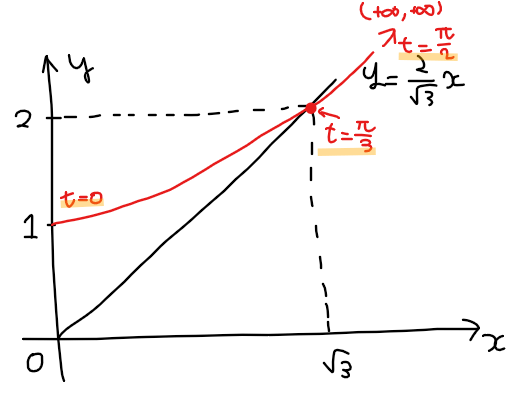

概形が把握できたので、求める面積を$\small S$とすると

\begin{split}
\small \displaystyle S &\small =\int_0^{\sqrt{3}}y dx-\color{blue}{（\mathsf{青色部分の三角形}）}\\
&\small \displaystyle =\int_0^{\frac{\pi}{3}}\frac{1}{\cos t}\cdot \frac{1}{\cos^2 t}dt -\frac{1}{2}\cdot \sqrt{3}\cdot {2}\\
&\small \displaystyle =\int_0^{\frac{\pi}{3}}\frac{1}{\cos^3 t}dt -\sqrt{3} \space \cdots (*)\\
\end{split}

●補足
問題解決のKeyでも記載した通り、定義域 $\small a≦x≦b$の範囲で関数$\small y=f(x)$と$\small x$軸で囲まれた面積は
\begin{split}
\small S &\small =\int_a^b y dx \\
\end{split}
で表される。本問の媒介変数表示の面積計算では、媒介変数$\small t$で積分がしたいので、$\small y$には$\small \displaystyle y=\frac{1}{\cos t}$、$\small dx$には
\begin{split}
&\small x=\tan t \\
\small \Leftrightarrow \space &\small dx =\frac{1}{\cos^2 t}dt\\
\end{split}
を代入し積分範囲も$\small t$の範囲に書き換えてあげれば変数$\small t$のみの積分になり計算ができる。

あとは、第1項目の積分

\begin{split}
&\small \displaystyle \int_0^{\frac{\pi}{3}}\frac{1}{\cos^3 t}dt\\
\end{split}

を求めるだけだ。

三角関数で分数型の積分では、分母と分子に$\small \sin t$と$\small \cos t$の組合せを作ることがポイントだった。今回であれば、$\small \cos t$のみの式になっているので、分母分子に$\small \cos t$を掛け算してあげることで

\begin{split}
&\small \displaystyle \int_0^{\frac{\pi}{3}}\frac{1}{\cos^3 t}dt\\
\small =&\small \displaystyle \int_0^{\frac{\pi}{3}}\frac{\cos t}{\cos^4 t}dt\\
\small =&\small \displaystyle \int_0^{\frac{\pi}{3}}\frac{\cos t}{(1-\sin^2 t)^2}dt\\
\end{split}

ここで、$\small u=\sin t$とおくと

\begin{cases}
\small \displaystyle <\mathsf{変数変換}>\\
\quad \small \displaystyle du=\cos t dt\\
\small \displaystyle <\mathsf{積分範囲}>\\
\small \displaystyle \quad t:0\to\frac{\pi}{3}\space \Rightarrow u:0\to\frac{\sqrt{3}}{2}\\
\end{cases}

となるので、

\begin{split}
&\small \displaystyle \int_0^{\frac{\pi}{3}}\frac{\cos t}{(1-\sin^2 t)^2}dt\\
\small =&\small \displaystyle \int_0^{\frac{\sqrt{3}}{2}}\frac{1}{(1-u^2)^2}du\\
\small =&\small \displaystyle \int_0^{\frac{\sqrt{3}}{2}}\left(\frac{1}{(1+u)(1-u)}\right)^2du\\
\small =&\small \displaystyle \int_0^{\frac{\sqrt{3}}{2}}\left[\frac{1}{2}\left(\frac{1}{1+u}+\frac{1}{1-u}\right)\right]^2du\\
\small =&\small \displaystyle \frac{1}{4}\int_0^{\frac{\sqrt{3}}{2}}\left[\frac{1}{(1+u)^2}+\frac{2}{(1+u)(1-u)}+\frac{1}{(1-u)^2}\right]du\\
\small =&\small \displaystyle \frac{1}{4}\int_0^{\frac{\sqrt{3}}{2}}\left[(1+u)^{-2}+(1-u)^{-2}\right]du\\
&\small \displaystyle \quad +\frac{1}{4}\int_0^{\frac{\sqrt{3}}{2}}\left[\frac{1}{1+u}+\frac{1}{1-u}\right]du\\
\small =&\small \displaystyle \frac{1}{4} \bigg[ -(1+u)^{-1} + (1-u)^{-1} \bigg]_0^{\frac{\sqrt{3}}{2}}\\
&\small \displaystyle \quad +\frac{1}{4}\bigg[\log(1+u)-\log(1-u)\bigg]_0^{\frac{\sqrt{3}}{2}}\\
\small =&\small \displaystyle \frac{1}{4} \bigg[\frac{2u}{1-u^2} \bigg]_0^{\frac{\sqrt{3}}{2}}+\frac{1}{4}\bigg[\log\frac{1+u}{1-u}\bigg]_0^{\frac{\sqrt{3}}{2}}\\
\small =&\small \displaystyle \frac{1}{4}\frac{\sqrt{3}}{1-\dfrac{3}{4}}+\frac{1}{4}\log\frac{2+\sqrt{3}}{2-\sqrt{3}}\\
\small =&\small \displaystyle \sqrt{3}+\frac{1}{4}\log\frac{(2+\sqrt{3})^2}{(2-\sqrt{3})(2+\sqrt{3})}\\
\small =&\small \displaystyle \sqrt{3}+\frac{1}{2}\log(2+\sqrt{3})\\
\end{split}

よって、$\small (*)$より、求める面積は

\begin{split}
\small S &\small \displaystyle =\color{#5c6bc0}{\int_0^{\frac{\pi}{3}}\frac{1}{\cos^3 t}dt}-\sqrt{3} \\
&\small \displaystyle =\color{#5c6bc0}{\sqrt{3}+\frac{1}{2}\log(2+\sqrt{3})}-\sqrt{3} \\
&\small \displaystyle =\color{red}{\frac{1}{2}\log(2+\sqrt{3})\space \cdots 【答】}\\
\end{split}

総評

解き方自体は面積を求める積分問題の王道であるが、（2）の積分 $$\small \displaystyle \int_0^{\frac{\pi}{3}}\frac{1}{\cos^3 t}dt$$ の計算が意外と骨が折れて大変。三角関数の積分処理能力と変数変換後の部分分数展開で次数を下げて積分する計算までの流れを確認できる良問だろう。

【問題2】媒介変数表示された曲線と面積（場合分けあり）（難易度：★★☆）

座標平面において、$\small t$を媒介変数として $$\small x=e^t \cos t+e^\pi,\space y=e^t \sin t \quad (0≦t≦\pi)$$ で表される曲線を$\small C$とする。曲線$\small C$と$\small x$軸で囲まれた部分の面積を求めよ。 [大阪大]

問題解決のKey

・面積を求める問題では、囲まれた部分の形を把握するために媒介変数表示された曲線の概形を把握することが重要。グラフの概形は、媒介変数表示された曲線の場合は5段の増減表をかくのが定石。
・面積を求める積分式の立式では、いきなり媒介変数での積分を考えるのではなく、$\small x$軸に沿った積分式を立式してから変数変換しよう。

　解説

まずはグラフの概形把握のために、増減表をかいておく。

\begin{split}
\small \displaystyle \frac{dx}{dt} &\small =e^t\cos t -e^t\sin t\\
&\small =e^t(\cos t -\sin t) \quad \cdots ①\\
\end{split}

$\small 0≦t ≦\pi$の範囲で、$\small \displaystyle \frac{dx}{dt}=0$になるときの$\small t$の値は、

\begin{split}
&\small e^t(\cos t -\sin t)=0\\
&\small \cos t -\sin t=0 \space (∵ \space e^t \neq 0)\\
&\small \tan t=1 \space (∵ \space \cos t \neq 0)\\
&\small \displaystyle ∴ \space t=\frac{\pi}{4}\\
\end{split}

同様に

\begin{split}
\small \displaystyle \frac{dy}{dt} &\small =e^t(\sin t+\cos t)\\
\end{split}

$\small 0≦t ≦\pi$の範囲で、$\small \displaystyle \frac{dy}{dt}=0$になるときの$\small t$の値は、

\begin{split}
&\small e^t(\sin t+\cos t)=0\\
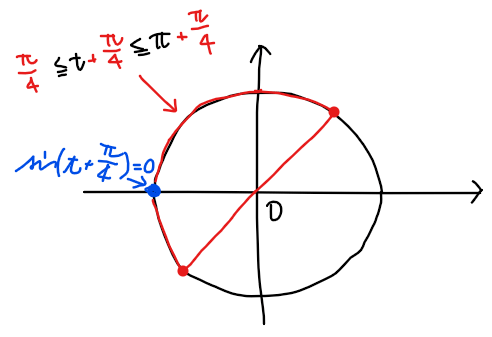
&\small \sqrt{2}e^t\sin\left(t+\frac{\pi}{4}\right)=0 \space \color{magenta}{◀\mathsf{三角関数の合成の利用}}\\
&\small \displaystyle ∴ \space t=\frac{3}{4}\pi\\
\end{split}

●補足
三角関数を含む方程式の解法は、「【徹底解説】三角方程式の解き方（三角関数の合成、2次関数の利用、角度の範囲から解く）」で詳しく解説しています。

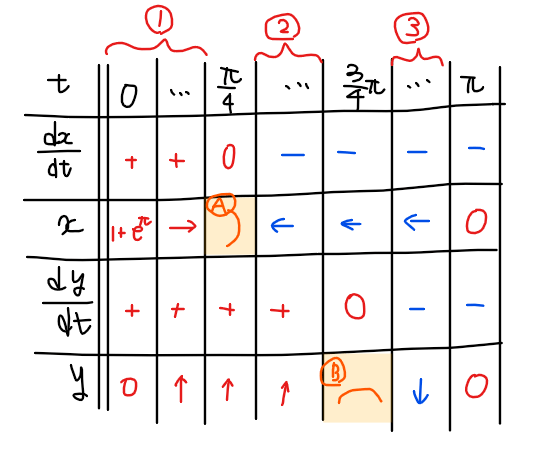
よって、増減表は下表のようになる。

●補足
$\small \displaystyle \frac{dx}{dt}$や$\small \displaystyle \frac{dy}{dt}$の符号は、$\small \displaystyle \frac{dx}{dt}=0、\frac{dy}{dt}=0$となる$\small t$の前後の値を具体的に代入することで確認すればよいでしょう。
媒介変数表示の増減表の書き方は参考書によっても様々ですが、個人的には上記の表がおすすめです。
特に、表中のAは$\small \displaystyle t=\frac{\pi}{4}$で$\small x$が右方向に増加している状態から左方向へ増加する（右方向へ減少する）状態へ変化するポイントになっているので、表中の「）」のようなカーブを描くことが分かります。
同様に、表中のBは$\small \displaystyle t=\frac{3}{4}\pi$で$\small y$が上方向に増加している状態から下方向へ増加する（上方向へ減少する）状態へ変化するポイントのため、表中の「⌒」のようなカーブを描くことが分かります。

増減表から、グラフの概形は以下のようになる。

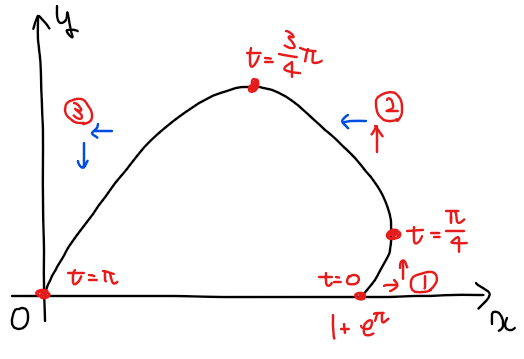
概形が把握できたところで、最後に囲まれた部分の面積を求める式を立式していく。

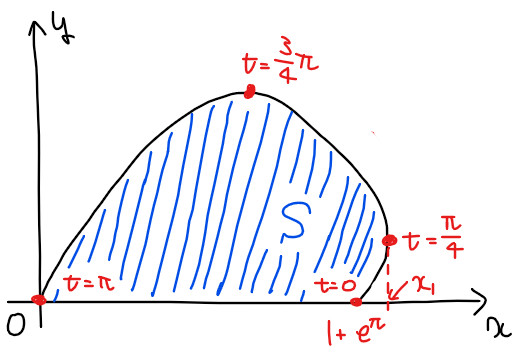
上図のように、$\small \displaystyle t=\frac{\pi}{4}$のときの$\small x$座標を$\small x_1$とし、求める面積を$\small S$とすると

\begin{split}
\small S &\small =\int_{x=0}^{x=x_1}y dx-\int_{x=1+e^\pi}^{x=x_1}ydx \quad [*1]\\
&\small =\int_{t=\pi}^{t=\pi/4}e^t\sin t \cdot e^t(\cos t-\sin t)dt\\
&\small \quad -\int_{t=0}^{t=\pi/4}e^t\sin t \cdot e^t(\cos t-\sin t)dt \quad [*2]\\
&\small =-\int_{\pi/4}^{\pi}e^{2t}(\sin t\cos t-\sin^2 t)dt \quad \color{magenta}{◀\mathsf{積分範囲の上下を入替}}\\
&\small \quad -\int_{0}^{\pi/4}e^{2t}(\sin t\cos t-\sin^2 t)dt\\
&\small =-\int_{0}^{\pi}e^{2t}(\sin t\cos t-\sin^2 t)dt \quad \color{magenta}{◀\mathsf{積分範囲を連結}}\\
\end{split}

[*1]補足
解説の都合上、媒介変数$\small t$ではなく、$\small x$に関する積分であることを明示するために
$$\small \color{red}{\int_{x=●}^{x=■}}ydx$$
という表記をしているだけなので、試験の解答では、通常通り
$$\small \int_{●}^{■}ydx$$
と記載すればOK。

[*2]補足
第一項目
\begin{split}
\small \int_{x=0}^{x=x_1}y dx\\
\end{split}
は、$\small y=e^t\sin t$、$\small \displaystyle dx=e^t(\cos t -\sin t)dt$（∵①）より
\begin{split}
&\small \int_{x=0}^{x=x_1}y dx \\
&\small =\int_{t=\pi}^{t=\pi/4}e^t\sin t \cdot e^t(\cos t-\sin t)dt\\
\end{split}
を得る。第二項目も同様。

ここで

\begin{split}
&\small \sin 2t=2\sin t\cos t\\
&\small \Leftrightarrow \space \sin t\cos t = \frac{1}{2}\sin 2t \space、\\
&\small \cos 2t=1-\sin^2 t\\
&\small \Leftrightarrow \space \sin^2 t=\frac{1-\cos 2t}{2}\\
\end{split}

より、

\begin{split}
\small S &\small =-\int_{0}^{\pi}e^{2t}(\sin t\cos t-\sin^2 t)dt\\
&\small =-\frac{1}{2}\int_{0}^{\pi}e^{2t}\sin 2tdt\\
&\small \quad +\frac{1}{2}\int_{0}^{\pi}e^{2t}(1-\cos 2t)dt\\
&\small =\frac{1}{2}\int_{0}^{\pi}e^{2t}dt -\frac{1}{2}\int_{0}^{\pi}e^{2t}(\sin 2t+\cos 2t)dt \space \cdots ②\\
\end{split}

第一項目は

\begin{split}
\small \frac{1}{2}\int_{0}^{\pi}e^{2t}dt &\small =\frac{1}{4}\bigg[e^{2t}\bigg]_0^\pi\\
&\small =\frac{1}{4}(e^{2\pi}-1)\space \cdots ③\\
\end{split}

第二項目は、自然対数と三角関数の積の積分なので、

\begin{split}
\small I=\frac{1}{2}\int_{0}^{\pi}e^{2t}(\sin 2t+\cos 2t)dt\\
\end{split}

とおき部分積分をすることで解くことができる（有名なやつですね(^^)/）。

\begin{split}
\small I &\small=\frac{1}{2}\int_{0}^{\pi}e^{2t}(\sin 2t+\cos 2t)dt\\
&\small=\frac{1}{2}\left(\bigg[\frac{1}{2}e^{2t}(\sin 2t+\cos 2t)\bigg]_{0}^{\pi} \right.\\
&\small \quad \left. -\color{#ef5350}{\frac{1}{2}\int_{0}^{\pi}e^{2t}(\cos 2t-\sin 2t)\cdot 2 dt}\right)\\
&\small=\frac{1}{2}\left(\frac{1}{2}(e^{2\pi}-1) \right.\\
&\small \quad \left. -\left(\color{#ef5350}{\bigg[\frac{1}{2}e^{2t}(\cos 2t-\sin 2t)\bigg]_{0}^{\pi}} \right.\right.\\
&\small \quad \left.\left. \color{#ef5350}{-\frac{1}{2}\int_{0}^{\pi}e^{2t}(-\sin 2t-\cos 2t) \cdot 2dt }\right)\right)\\
&\small=\frac{1}{2}\left(\frac{1}{2}(e^{2\pi}-1)\right.\\
&\small \left. \quad -\frac{1}{2}(e^{2\pi}-1)\right.\\
&\small \left. \quad -\int_{0}^{\pi}e^{2t}(\sin 2t+\cos 2t)dt\right)\\
&\small =\frac{1}{2}I\\
\end{split}

ゆえに、

\begin{split}
&\small I=\frac{1}{2}I\\
\small ∴ \space &\small I=0\\
\end{split}

よって、②と③より求める面積は

\begin{split}
\small S &\small =\color{red}{\frac{1}{4}(e^{2\pi}-1)\space \cdots 【答】}\\
\end{split}

総評

面積計算の立式は、いきなり媒介変数$\small t$に関する積分式を考えようとすると混乱してしまい \begin{split} \small S &\small =\int_{\pi/4}^{\pi}e^t\sin t \cdot e^t(\cos t-\sin t)dt\\ &\small \quad -\int_{0}^{\pi/4}e^t\sin t \cdot e^t(\cos t-\sin t)dt\\ \end{split} のような立式ミスにつながる可能性が高い。なので、まずは解答のように$\small x$に関する積分式を立式した後に、変数変換する方針で考えよう。