単位円ってどう書くの？三角比の拡張（三角方程式）の解き方をsin、cos、tanごとに分かりやすく解説

今回は、三角比の拡張として、0°～90°を超えた角度について三角比をどう求めるかを解説していきます（ちなみに、今回扱う問題は三角比を含む方程式のため、三角方程式と呼ばれます）。「単位円の書き方が分からない」、「sin、cos、tanが単位円のどの部分なのか分からない」という悩みに対してsin、cos、tanのそれぞれのパターンごとに三角比の求め方を解説するので、ぜひ最後まで読んでみてください！

広告

広告

1.三角方程式の解法

突然ですが、以下の問題を解けますか？

「\(\small \theta = \frac{7}{6}\pi、\frac{11}{6}\pi \)が答え！…」と思った人は要注意！三角方程式の解き方を完全には理解できてないかもしれません。

この問題の正しい答えは、\(\small \theta = -\frac{5}{6}\pi、-\frac{\pi}{6} \)…(答)になります。

今回は、単位円を利用した三角方程式の問題と解法をsin、cos、tanにパターンに分けて解説していきます！冒頭の問題が解けなかった人もどうやったら正解にたどり着けるのかをステップごとに丁寧に解説しているので、ぜひ一緒に見ていきましょう！また、「解けた！」という人は実力チェックもかねて他のパターンもしっかり解けるか確認していきましょう！

1.1 単位円の使い方

三角方程式の問題を解くにあたって一番重要なのは、いうまでもなく単位円の使い方です。なので、まず初めに単位円の使い方について解説していきます。

なお、問題を解くときの思考回路が分かりやすいように、私が問題を解くときに考えていることをそのまま書くので、数学的な正確性は若干無視されますがご了承ください。。。

まず、「なんで単位円なんか使うの？」という疑問ですが、理由は単純にわかりやすいからです。私は、\(\small \sin\theta=-\frac{1}{2}\)と言われても、\(\small \theta\)が何度か覚えてないので、さっぱりイメージがわきません。なので、単位円を描いてイメージを付けています。

では、皆さんはどんなふうに単位円をかきますか？ここでは、「私の場合はこうだよ」というのを紹介します。単位円の書き方は簡単に言うと以下の3STEPです。

次章で詳しく解説していきます！

1.2 単位円を使った解法3ステップ

STEP1

解の位置を特定

まず円を描いたら、今回求めるのは\(\small \sin\theta\)なのでy座標に\(\small -\frac{1}{2}\)の線を引きます。

sinの値はy座標、cosの値はx座標になります。なんでかという説明は教科書などに書かれているので割愛しますが、単純な理由なので調べてみましょう。今回は、sinの値が\(\small -\frac{1}{2}\)なので、y座標が\(\small -\frac{1}{2}\)に線を引きました。次に、円と線が交わった部分（図の赤点）に棒を伸ばします。ここが解の位置になります。

STEP2

三角形を特定

下図のような三角形を考えて、そこに、sinの値を書き込みます。sinの値が\(\small -\frac{1}{2}\)なので、斜辺が、2で縦の辺が-1です。

この時に、座標がマイナスの辺は、符号をマイナスにしておくと良いと思います。単位円は、半径が1の円を指すので、しれっと半径が2になっているのがおかしいですが、あくまで比を知るためには便利なので私はいつもこうしています。すると、赤色の三角形は辺の比が\(\small 1:2:\sqrt{3}\)の三角形なので、青色の角度は、30°とわかります。ラジアンで表せば、\(\small \frac{\pi}{6}\)の三角形であることが分かりました。

STEP3

角度を求める

最後に、実際に求める角度は先程求めた三角形の角度ではなく、単位円上の角度なので、ここからはその角度を求めます。とはいえ、角度というのは、360°一周すると同じところに戻ってしまうので「どこから計った角度なのか？」、「何周目なのか？」、「時計回りか？反時計回りなのか？」によって、角度は様々な表し方ができてしまいます（下図参照）。

なので、たいていの問題では、角度はこの範囲で考えればいいですよ、という前書きがあります。例題で言えば、「\(\small -\pi ≦ \theta ≦ \pi\)のとき」がそれに該当します。
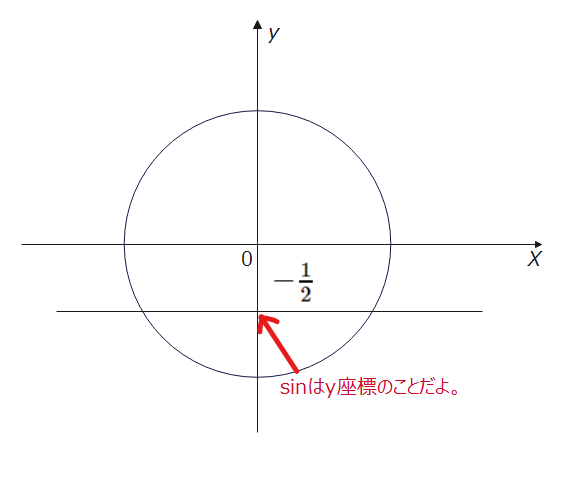
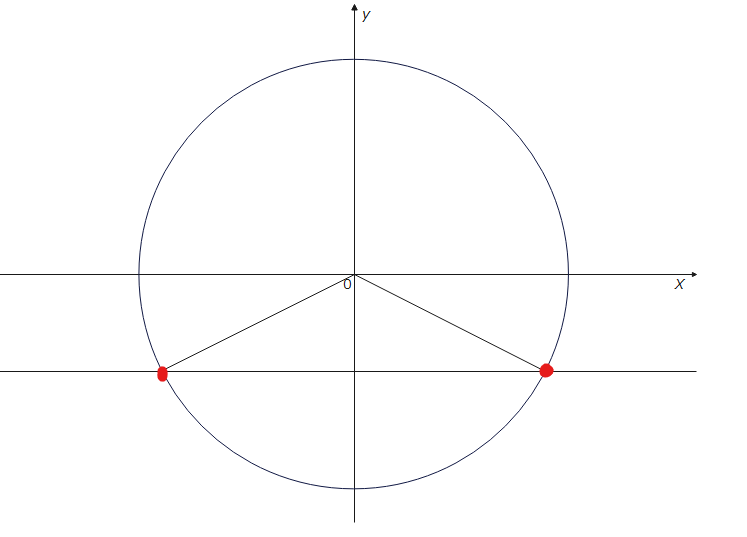
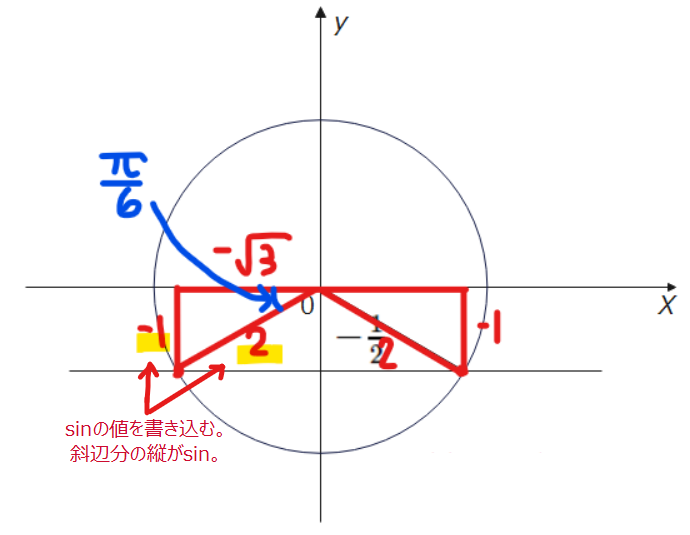
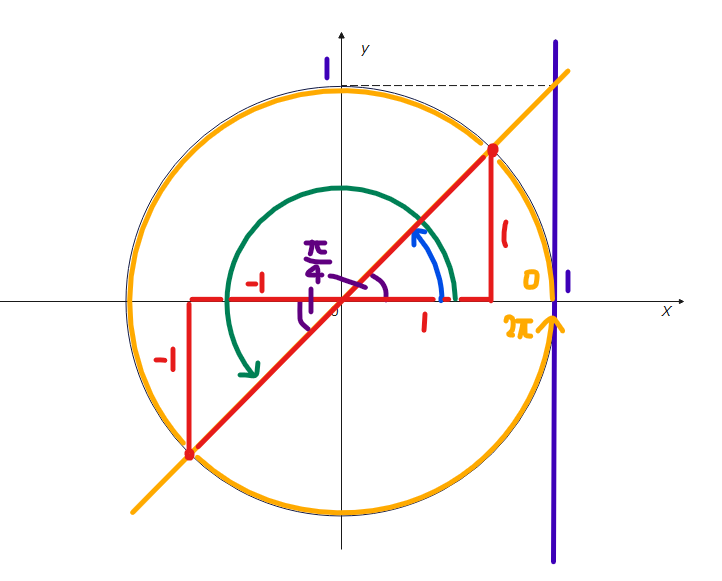
角度を求める際には以下の図を描きましょう。

オレンジは、今回考える角度の範囲（\(\small -\pi≦\theta≦\pi\)）、赤い三角形と紫の角度はstep2で特定した三角形の情報、そして青と緑が求める角度です。 角度を求めるときに注意したいのは、0°からの角度を求めるということ。範囲の開始地点からの角度ではないので注意しましょう！

あとはそれぞれの角度を求めればOK。青い角度は、紫の角度と同じなので\(\small \frac{\pi}{6}\)…としてしまいそうですが、単位円上の角度には＋－があるので注意が必要です。

★補足★
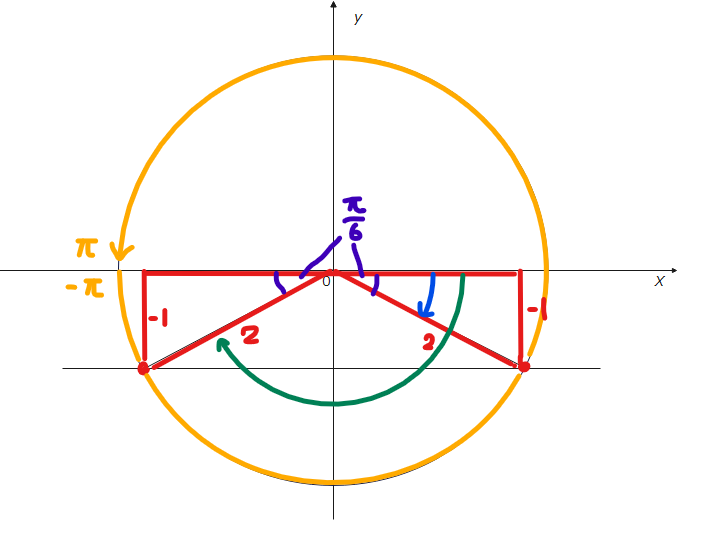
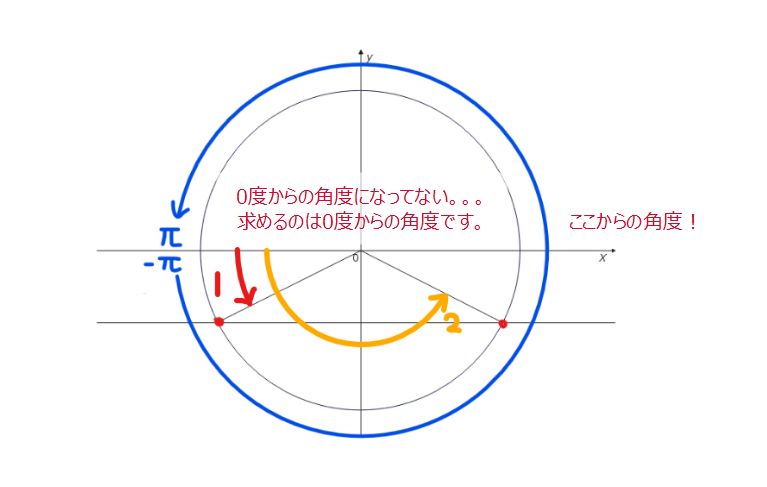
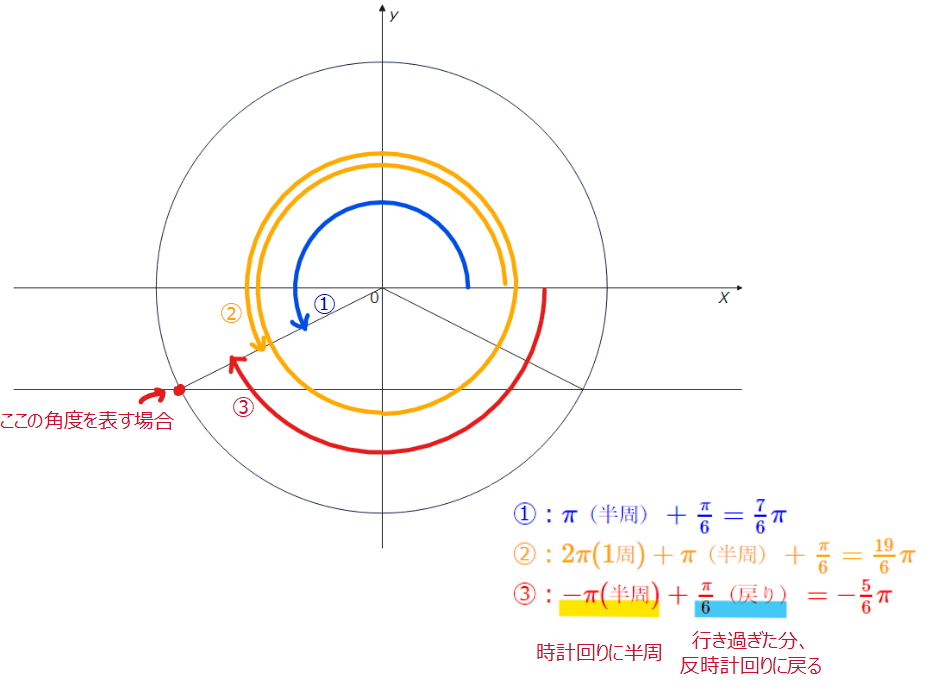
単位円の角度には、＋と－があり、反時計回りは＋、時計回りは－と決まっているので、注意しましょう。

よって、青色の角度は、\(\small -\frac{\pi}{6}\)です。緑色の角度はいろいろな求め方があります。下の図のように、一旦、\(\small -\pi\)(青色)まで進んでから、\(\small ＋\frac{\pi}{6}\)戻る(黄色)と緑色の角度になることが分かるので、\(\small -\pi＋\frac{\pi}{6}=-\frac{5}{6}\pi\)です。戻ったりするのが面倒…ということであれば、シンプルに一旦プラスマイナスのことは忘れて180°から30°引いた150°が緑の角度だからラジアンにすると\(\frac{5}{6}\pi\)で、あとは、0°から時計回りに進んでるので「－」つけて\(-\frac{5}{6}\pi\)だな、で全然okです。

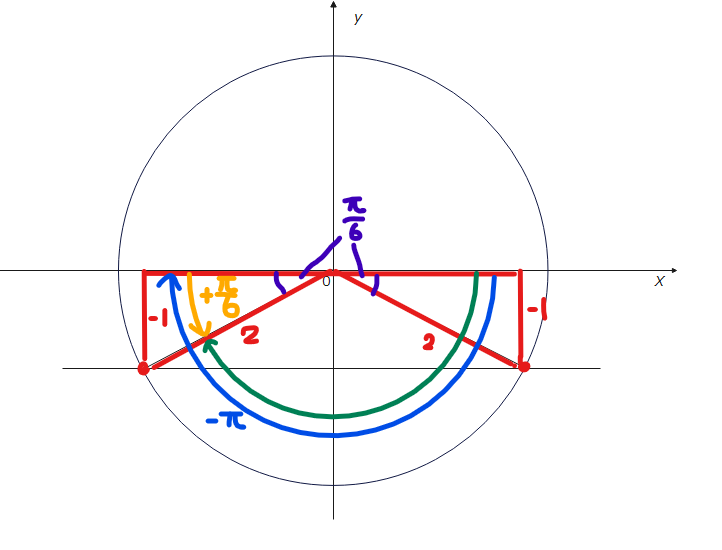
よって答えは、\(\small \theta = -\frac{\pi}{6}、-\frac{5}{6}\pi\space\cdots(答)\).

1.3 三角方程式-サイン編

解答

例題1と解くべき式は同じですが、角度の範囲が異なっています。\(\small \sin \theta = -\frac{1}{2}\)の位置と三角形を特定するところまでは、例題1と同じなので割愛します。

では、角度を求めていきましょう。例題1では、\(\small -\pi ≦ \theta ≦ \pi\)の範囲でしたが、今回は、\(\small 0 ≦ \theta < 2\pi\)です。

オレンジが、今回考える範囲（\(\small 0 ≦ \theta < 2\pi\)）で、0～\(\small 2\pi\)までの間に、2個解（赤丸）があるので、それぞれの角度（青と緑）を求めればよいです。
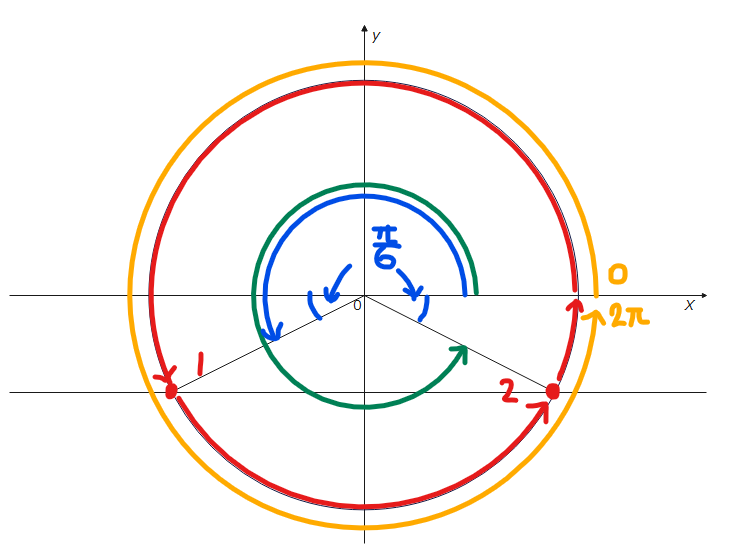
角度を求めるときは、下の図のようにきりの良い角度(\(\small \pi、2\pi\))から足し引きして考えると求めやすいです。青の角度は\(\small \theta= \pi+\frac{\pi}{6}=\frac{7}{6}\pi\)、緑の角度は、オレンジ色の角度を考えて、\(\small \theta=2\pi-\frac{\pi}{6}=\frac{11}{6}\pi\)とするとわかりやすいです。
ちょっと小難しいことを言うと、補足でも書きましたが、時計回りは－、反時計回りは＋の角度となるので、緑色の角度を求めるときには、反時計回りに\(\small 2\pi\)進んだ後に、時計回りに\(\small -\frac{\pi}{6}\)進むと考えるとよいです。図にマイナスをつけているのはそういう意味です。

よって答えは、
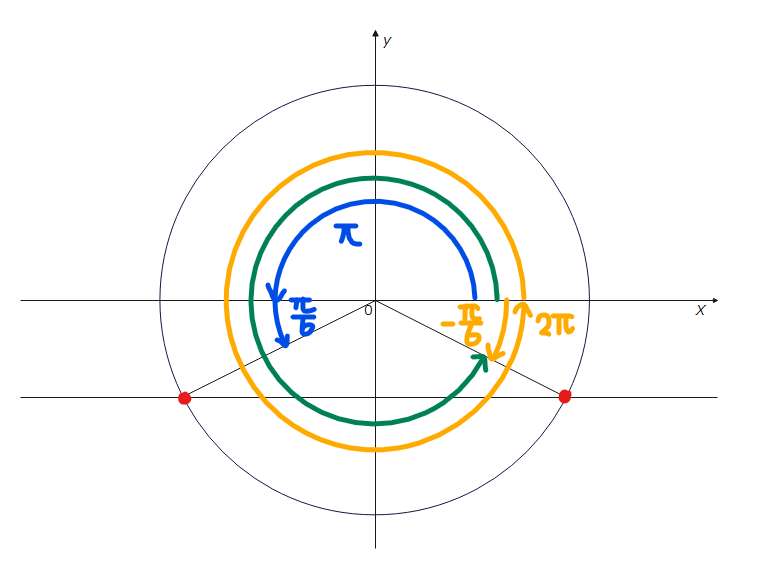
\(\small \theta = \frac{7}{6}\pi、\frac{11}{6}\pi\space \cdots\)(答)

1.4 三角方程式-コサイン編

解答

今回はcosですので、x座標を見ることになりますが、解き方は同じなので、例題の解き方を参考に解いていきましょう。 まずは解の位置を特定しましょう。

こんな感じ。sinの時は、y座標でしたが、cosなのでx座標が\(\small \frac{1}{2}\)のところに線を引きます。
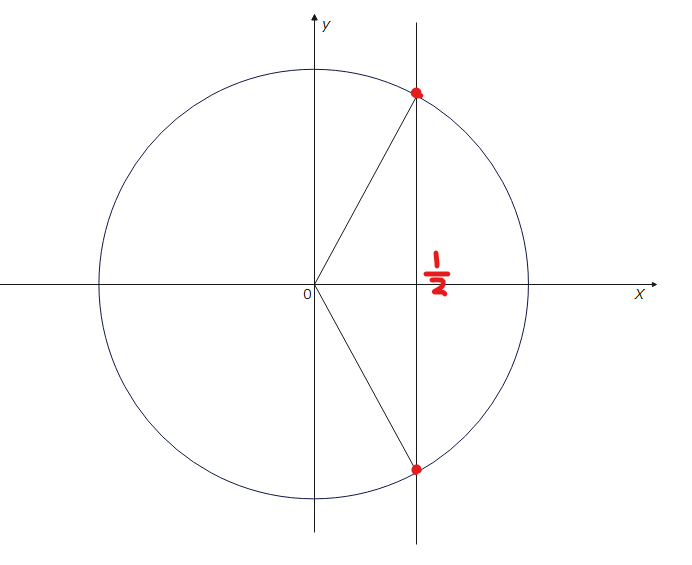
続いて三角形を特定します。

cosが\(\small \frac{1}{2}\)なので、上の図から、辺の比が1:2:\(\small \sqrt{3}\)の三角形とわかるので、青色の角度は、60°ですね。ラジアンで言えば、\(\small \frac{\pi}{3}\)。最後に、角度を求めたいので、必要な情報を図に書き込みます。

上の図のようなものが書ければよいです。今回求める解は1と2で、求める角度は、青と緑です。青の角度は図からすでに\(\small\frac{\pi}{3}\)です。緑の角度は、\(\small \theta=2\pi-\frac{\pi}{3}=\frac{5}{3}\pi\)です。
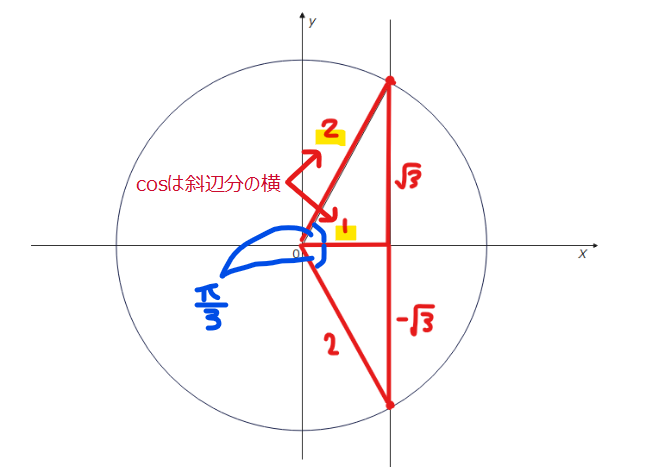
よって、 \(\small \theta = \frac{\pi}{3}、\frac{5}{3}\pi\space \cdots\)(答)

1.5 三角方程式-タンジェント編

解答

tanを求める三角方程式はあまり登場しませんが、いざという時に解けないと困るので解説します。
最初に皆さん無意識にやっていると思いますが、式変形して、「三角比=数字」の形にしておきましょう。今回だと、
\(\small \tan \theta +\sqrt{3}= 0\)
\(\small \tan \theta = -\sqrt{3}\)。
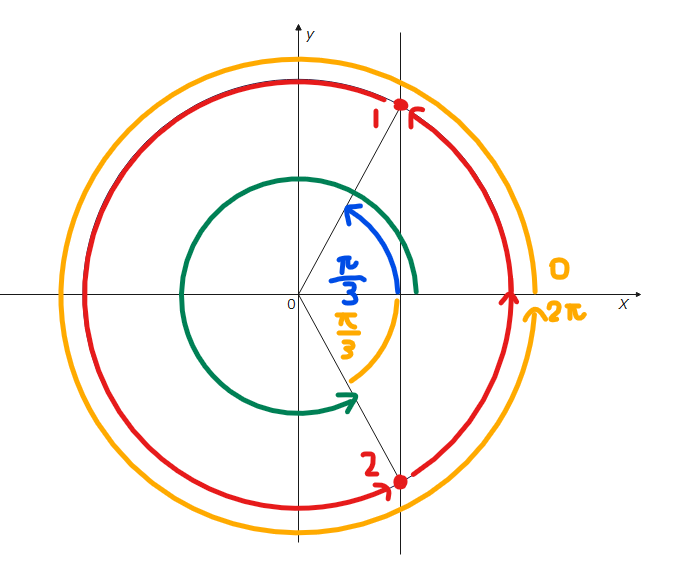
まず、解の位置を特定しますが、sinはy座標、cosはx座標でしたが、tanはどう考えればいいでしょうか？ちょっと特殊で tanの場合は斜めに線を引きます。引き方は以下の図の通り。

まず、x=1の線（青色の線）を引きます。次に、y座標がtanの値になるので、今回だとy座標が\(\small -\sqrt{3} \)の部分に点を付けます（青丸）。最後に、tanの値を通るように斜め線を引けば、単位円との交点が求める解の位置になります。さらっと流しましたが、「どうしてx=1の線を引くの？」、「どうしてy座標がtanの値なの？」、「どうして斜めに線を引いて単位円と交わる場所が解の位置なの？」と思った方は、補足に理由を書いているので確認してみましょう。

★補足-上の手順でなぜtanが求まるのか？★
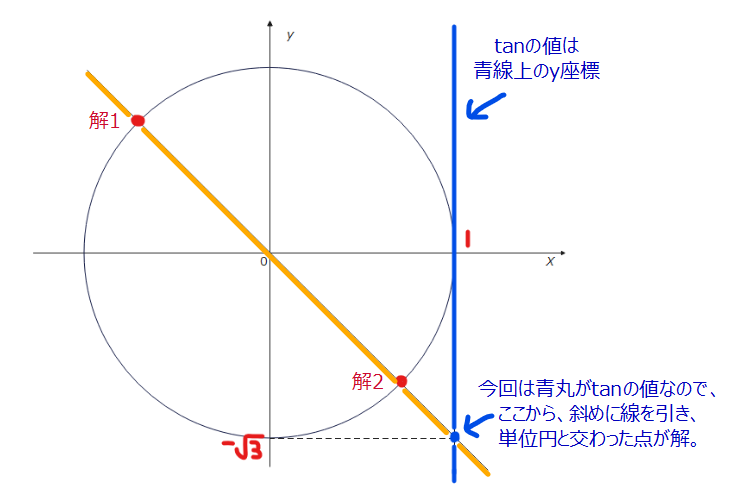
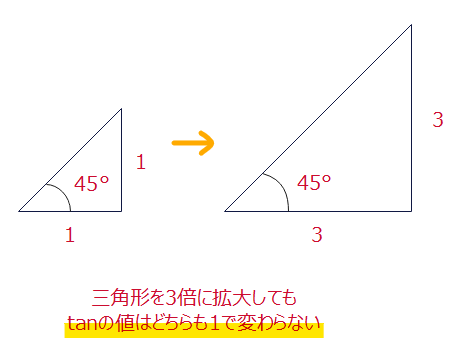
前提として、tanの値は、三角形の横の辺分の縦の辺で求めることができます。また、三角比なので、あくまで比であることから、三角形を拡大or縮小しても角度が同じである限り三角比は変わりません。あとでこの知識を使うので覚えておいてください。

では、本題で、今回x=1に線を引き、下図のオレンジ色の三角形を考えます。すると、tanの値は横の辺（赤）分の縦の辺（青）(正確には座標なのでマイナスになることもありますがあまり気にせず…)、すなわち\(\small \frac{-\sqrt{3}}{1}=-\sqrt{3}\)となり、確かに問題文で求めたいtanになっています。ポイントは、x=1に線を引くと tanの分母である横の辺が必ず1になるので、y座標をtanの値と考えることができるのでわかりやすいため、ここで考えているわけです。 理由はそれだけです。

ここで勘のいい人であれば気づいたかもしれませんが、今まで求めてきた三角形は単位円上でどんな三角形かを考えていました（例題1～3を見てみましょう）。tanの求めやすさを重視するがあまり、単位円上で考えるのを忘れていたわけです。単位円上で考えないと、解の位置が分からないですよね。でも大丈夫。ここで最初に説明した知識を思い出しましょう。三角形を拡大or縮小しても三角比は変わりませんね。なので、下の図の緑の三角形もtanの値は\(\small -\sqrt{3}\)です。なので、結果的に、斜めの線と単位円の交わる点を解の位置と考えればよいわけです。

次は、三角形を特定します。以下の図より今回は、辺の比が1:2:\(\small \sqrt{3}\)なので、60°の三角形です。

ここまで書ければ、いつもと同様、角度を求めるために必要な情報を書き込みます。

こんな感じで描ければgood。あとは角度を求めるだけです。
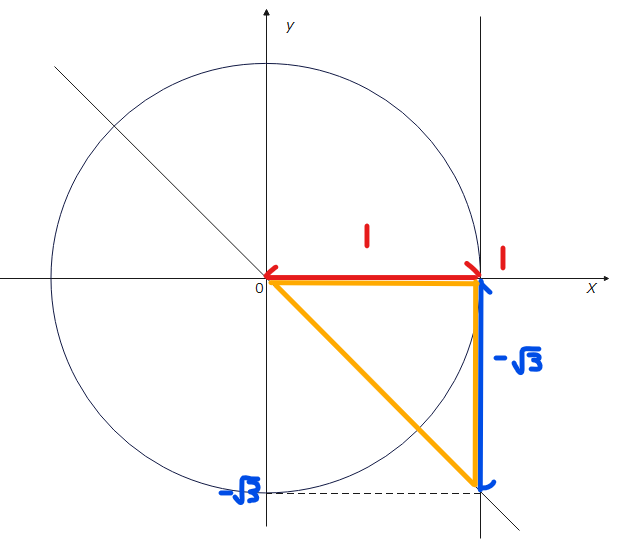
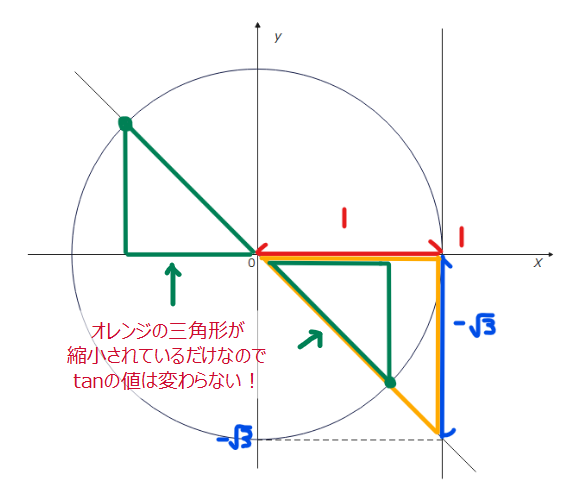
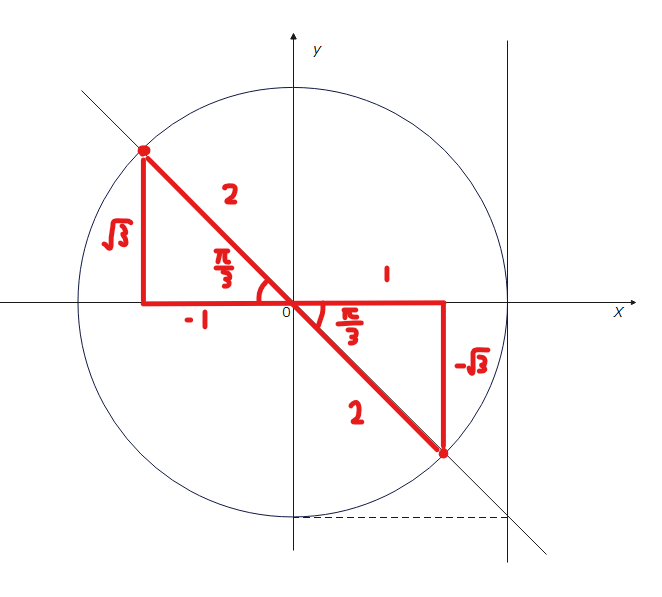
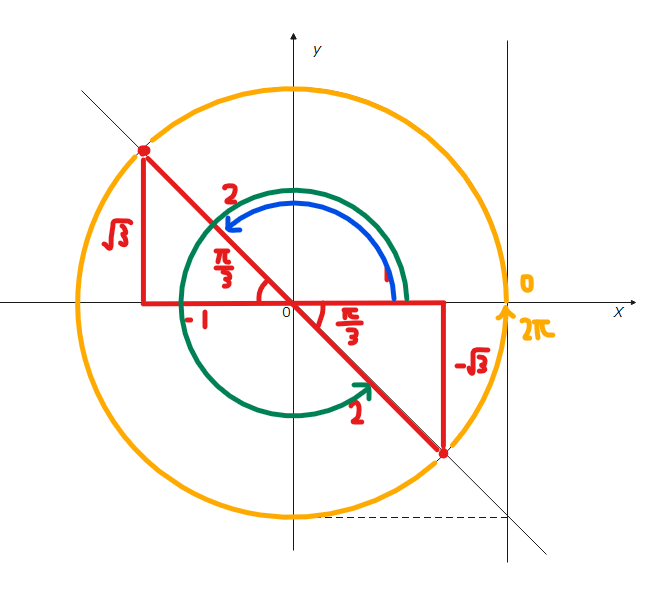
\(\small \theta = \pi-\frac{\pi}{3}=\frac{2}{3}\pi\)。
\(\small \theta = 2\pi-\frac{\pi}{3}=\frac{5}{3}\pi\)。
\(\small \theta = \frac{2}{3}\pi、\frac{5}{3}\pi\space \cdots\)(答)

2.三角方程式の練習問題

解答

(1)\(\small -\frac{\sqrt{2}}{2}\)が見慣れない値をしていますが、\(\small \sqrt{2}\)があるのでなんとなく 45°かな、という予想はついたかもしれません。ちょっと式変形にコツがいりますが、分母分子に\(\small \sqrt{2}\)を掛け算すると
\(\small -\frac{\sqrt{2}}{2}=-\frac{\sqrt{2}×\sqrt{2}}{2×\sqrt{2}}=-\frac{2}{2×\sqrt{2}}=-\frac{1}{\sqrt{2}}\)
です。三角比はパターンが決まっているので覚えておくとよいでしょう。図は以下の通り。

求める角度は
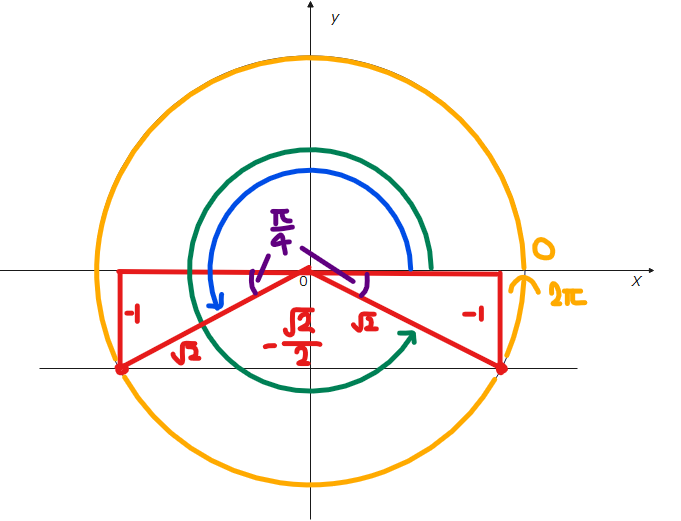
\(\small \theta = \pi+\frac{\pi}{4}=\frac{5}{4}\pi\)。
\(\small \theta = 2\pi-\frac{\pi}{4}=\frac{7}{4}\pi\)。
よって、\(\small \theta = \frac{5}{4}\pi、\frac{7}{4}\pi\space \cdots\)(答)
(2)こちらも最初に式変形すると、\(\small　\cos \theta = -\frac{\sqrt{3}}{2}\)です。

求める角度は
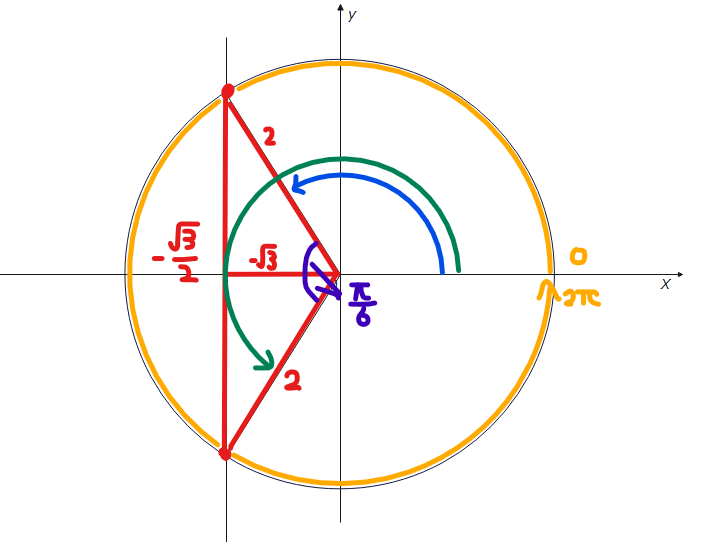
\(\small \theta = \pi-\frac{\pi}{6}=\frac{5}{6}\pi\)。
\(\small \theta = \pi+\frac{\pi}{6}=\frac{7}{6}\pi\)。
よって、\(\small \theta = \frac{5}{6}\pi、\frac{7}{6}\pi\space \cdots\)(答)
(3)以下の図より、求める角度は、
\(\small \theta = \frac{\pi}{4}\)。
\(\small \theta = \pi+\frac{\pi}{4}=\frac{5}{4}\pi\)。
よって、\(\small \theta = \frac{\pi}{4}、\frac{5}{4}\pi\space \cdots\)(答)

まとめ