今回は、三角関数の合成公式について解説します。三角関数は公式が多いので、いくつかのパートに分けて解説しています。加法定理と三角比の基本公式、2倍角、半角、3倍角の公式はこちらのリンクから飛べるので、よかったら併せて確認してみて下さい!
はじめに
今回は三角関数の合成の攻略法について解説します。この記事を読めばあの複雑な公式も覚えるべきなのか、覚えなくても理解すればいいのかなどわかるようになっているのでぜひ最後まで読んでみてください!
本記事で扱う公式
三角関数の合成
三角関数の合成の公式スペック
公式の攻略法
暗記か導出か
皆さん、三角関数の合成の公式は覚えるべきか、覚えなくても良いのかが一番気になっている部分だと思うので、初めに結論を言っちゃいます。結論、暗記がおすすめです。理由は、導出するにも式変形が特殊なため、結局式変形の方法自体を覚える必要があるからです。どうせ覚えるなら、個人的には公式を覚えようって感じです。
ただ、今回は正直、公式自体を暗記するのか導出方法を暗記するのかは、人によって意見が分かれそうなくらいどちらも微妙なので、ここからは、暗記のメリット・デメリットと、導出のメリット・デメリットをそれぞれ解説していきたいと思います。最後には、暗記と導出のデメリットを補った折衷案も紹介するので、この記事で皆さんがどの方法に向いているのか診断してみましょう。ちなみに、どちらが良くて、どちらが悪いということはないので、自分に合ったやり方を見つけていきましょう!
公式暗記と公式導出のメリット・デメリット
結論、それぞれのメリット・デメリットを簡単にまとめると以下の通りです。
■公式暗記
★メリット
・導出のための数式計算が不要
★デメリット
・忘れてしまう可能性が高い(特に、\(\small \sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\)、\(\small \cos\alpha=\frac{a}{\sqrt{a^2+b^2}}\)の部分)
■公式導出
★メリット
・暗記が難しい\(\small \sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\)、\(\small \cos\alpha=\frac{a}{\sqrt{a^2+b^2}}\)を覚えなくてよい
・応用問題に対応できる
★デメリット
・式変形が難しい
【公式暗記】メリット
公式暗記のメリットは以下の通りです。
- 覚えるのが大変なほど複雑な公式ではない
- 導出するにしても暗記が必要なら公式自体を暗記したほうが効率的
- 暗記することで数式計算を回避できる
暗記が得意なのであれば暗記しちゃいましょう。あとは、式を導出すること自体に苦手意識がある人は、思い切って暗記してしまう方が近道です。
【公式暗記】デメリット
暗記することのデメリットを挙げるとするならば、忘れてしまう可能性が高いということです。この公式は使用頻度がそれほど高いわけではないので、たまに出てきたときに忘れてしまうという可能性が高いと思います。なので、対策として定期的に復習するのがよいかと思います。
【公式導出】メリット
公式導出のメリットは以下の通りです。
- 公式を忘れても頑張れば導出できる
- 公式の成り立ちを理解しているので応用力が増す
1点目の公式導出については以下の計算方法で導くことができます。
■三角関数の合成公式の導出方法
$$
\begin{equation}
\begin{split}
&a\sin\theta+b\cos\theta\\
&=\color{red}{\sqrt{a^2+b^2}}\left(\frac{a}{\color{red}{\sqrt{a^2+b^2}}}\sin\theta+\frac{b}{\color{red}{\sqrt{a^2+b^2}}}\cos\theta\right)\\
&=\sqrt{a^2+b^2}\left(\sin\theta\color{blue}{\frac{a}{\sqrt{a^2+b^2}}}+\cos\theta\color{green}{\frac{b}{\sqrt{a^2+b^2}}}\right)\\
&=\sqrt{a^2+b^2}\left(\sin\theta\color{blue}{\cos\alpha}+\cos\theta\color{green}{\sin\alpha}\right)\\
&=\sqrt{a^2+b^2}\sin(\theta+\alpha)\\
\end{split}
\end{equation}
$$
公式暗記の時に若干覚えるのが大変な\(\small \sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\)、\(\small \cos\alpha=\frac{a}{\sqrt{a^2+b^2}}\)の部分が式変形の過程で自然に出てくることがメリットです。
2点目の応用力が増すについては、例えば、次のような問題にも応用が利きます。
■問題
次の空欄に当てはまるものを選べ。
$$a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\cos(\boxed{\phantom{hoge}})$$
【選択肢】
a. \(\small \theta+\alpha\), b. \(\small \theta-\alpha\)
ただし、\(\small \sin\alpha=\frac{a}{\sqrt{a^2+b^2}}\)、\(\small \cos\alpha=\frac{b}{\sqrt{a^2+b^2}}\)とする。
■解答
$$
\begin{equation}
\begin{split}
&a\sin\theta+b\cos\theta\\
&=\color{red}{\sqrt{a^2+b^2}}\left(\frac{a}{\color{red}{\sqrt{a^2+b^2}}}\sin\theta+\frac{b}{\color{red}{\sqrt{a^2+b^2}}}\cos\theta\right)\\
&=\sqrt{a^2+b^2}\left(\color{blue}{\sin\alpha}\sin\theta+\color{blue}{\cos\alpha}\cos\theta\right)\\
\end{split}
\end{equation}
$$
ここで、青字部分は問題文の条件、\(\small \sin\alpha=\frac{a}{\sqrt{a^2+b^2}}\)、\(\small \cos\alpha=\frac{b}{\sqrt{a^2+b^2}}\)を代入した。
$$
\begin{equation}
\begin{split}
(\textrm{与式})&=\sqrt{a^2+b^2}\left(\color{red}{\cos\alpha\cos\theta+\sin\alpha\sin\theta}\right)\\
&=\sqrt{a^2+b^2}\color{red}{\cos(\theta-\alpha)}\\
&\quad \textrm{※赤字箇所は、加法定理を利用}\\
\end{split}
\end{equation}
$$
よって、答えは、b. \(\small \theta-\alpha \quad \cdots\)(答)
このような問題は、公式を丸暗記しているだけでは解くことができず、公式の導出過程を理解しているからこそ応用が利く式変形ができます。
【公式導出】デメリット
公式導出のデメリットは、何といっても式変形が特殊ということです。改めて導出方法を見返すと、はじめに\(\small \sqrt{a^2+b^2}\)で全体をくくったり、途中で突然\(\small \cos\alpha\)、\(\small \sin\alpha\)がでてきたりと、「加法定理を使うことを見越した戦略的な式変形」になっています。いつものようにただ計算を進めていけばいい式変形とはわけが違うという点で、「この変形を覚えるくらいなら暗記しちゃった方が楽」と思った人も多いはずです。
三角関数の合成はこれで解ける!
ここまで、公式暗記vs公式導出でメリデメを紹介しましたが、それぞれのメリットを活かして、デメリットを相殺するような「第3の方法」はないのでしょうか?
結論、第3の方法はあります。その方法とは一言でいうと「図とコラボで暗記」です。
この方法は私自身が現役高校時代に使っていたおすすめの暗記方法なので、最後に紹介させていただきます。
図とコラボで解くのがおすすめ
この方法は、ベースは「公式暗記」になります。なので式の導出はありません。そのうえで、公式暗記のデメリットである\(\small \sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\)、\(\small \cos\alpha=\frac{a}{\sqrt{a^2+b^2}}\)の部分を図を描くことで回避するという方法です。
では、具体的に説明していきます。覚えるべきは、たった一つで
$$a\sin\theta+b\cos\theta$$
に対して、以下のような単位円を描くことです。
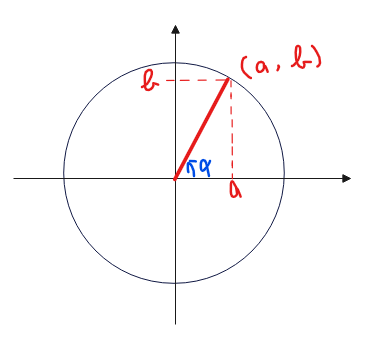
これだけです。サインとコサインの係数を座標にとって、角度を\(\small \alpha\)とおく。
これだけ描けてしまえば、あとはこの単位円の半径を合成後のサインの係数に、角度を\(\small \alpha\)とすればokです。
■三角関数の合成方法
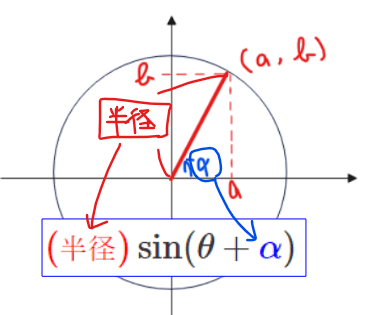
■補足:なぜ、これで求められるのか
なんでこれで求められるのかは、この単位円のサインコサインを求めてみると、
$$
\begin{equation}
\begin{split}
&\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\\
&\cos\alpha=\frac{a}{\sqrt{a^2+b^2}}\\
\end{split}
\end{equation}
$$
となり、三角関数の合成の定義に当てはまるからです。逆に言うと、三角関数の合成の公式で数式で表されている角度\(\small \alpha\)の定義を単位円で可視化するとこのようになるといえます。
単位円を描くときの注意点
元の式から単位円を描くときに注意点が2つあります。例えば、\(\small 2\sin\theta-2\cos\theta\)の合成をしたいときは、単位円はこうなります。
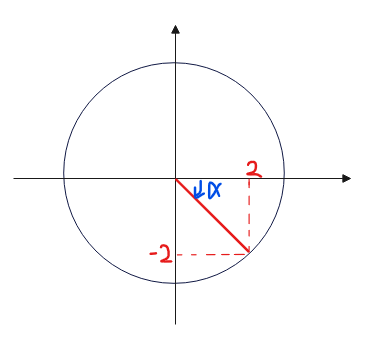
ここで1点目の注意点が、「係数の符号を含めて座標にする」必要があるということです。今回ならば(2,-2)に点を打ちに行きます。間違っても(2,2)ではないので符号には注意しましょう。
2点目が「角度\(\small \alpha\)のとり方」です。単位円の中にも青色で描いている通り、マイナス方向に角度を測ります。今回の場合は、図から\(\small \alpha=-\frac{\pi}{4}\)と反対方向に図るので「マイナス」の符号が付きます。\(\small \alpha=\frac{\pi}{4}\)としないように注意しましょう。また、通常\(\small \alpha\)は180°を超えない(マイナスなら、-180°を超えない)範囲で表すので、右回りか左回りの近い方で角度を測るようにしましょう(今回だったら、\(\small \alpha=\frac{7}{4}\pi=315°\)は180°超えるのでダメ)。
話が逸れましたが、以上の注意点を踏まえると、三平方の定理から半径が\(\small 2\sqrt{2}\)、角度\(\small \alpha=-\frac{\pi}{4}\)なので、答えは\(\small 2\sqrt{2}\sin\left(\theta-\frac{\pi}{4}\right)\quad \cdots\)(答)となります。
まとめ
今回は三角関数の合成公式の攻略方法を、公式暗記か公式導出か、それとも第3の方法「図とコラボで暗記」かという観点で解説しました。いろいろと紹介したんですが、個人的には「図とコラボで暗記」が一番忘れにくくおすすめなので、ぜひマスターできるように問題を通して使いこなしてみてください。
欲を言うと、「図とコラボで暗記」したうえで導出方法も頭の片隅に入れておく、これができたら最強だと思います。なので、使いこなせるようになってきたら、導出方法も覚えておきましょう。導出方法の暗記方法は、「\(\small \sqrt{a^2+b^2}\)でくくってから加法定理に持っていく」、これで私は覚えてます。
では本日はここまでです。お疲れさまでした!






コメント