【三角関数の公式一覧】2倍角、半角、3倍角の公式(sin、cos、tan)をまとめて覚える方法とは？

今回は、2倍角、半角、3倍角の公式について、よくセットで出てくる公式をまとめて覚える方法について解説します。三角関数は公式がめちゃくちゃ多いので、いくつかのパートに分けて解説しています。加法定理や三角関数の基本公式について知りたい人は、リンクから確認してみて下さい！

はじめに
★本記事で扱う公式
1. 2倍角、半角、3倍角の公式
2. 2倍角、半角の公式のスペック
★公式の解説
1. “〇倍角の公式”攻略の結論
まとめ

はじめに

今回は2倍角、半角、3倍角の公式の攻略法を解説します。三角関数の分野では必ずと言っていいほど出てくる公式なので、ぜひ一緒に覚える公式を減らしていきましょう！

★本記事で扱う公式

2倍角、半角、3倍角の公式

2倍角の公式

$$ \begin{equation} \begin{split} &\sin2\theta=2\sin\theta\cos\theta\\ \end{split} \end{equation} $$ $$ \begin{equation} \begin{split} \cos2\theta&=2\cos^2\theta-1\\ &=1-2\sin^2\theta\\ \end{split} \end{equation} $$ $$ \begin{equation} \begin{split} \tan2\theta=\frac{2\tan\theta}{1-\tan^2\theta}\\ \end{split} \end{equation} $$

半角の公式

$$ \begin{equation} \begin{split} &\sin^2\frac{\theta}{2}=\frac{1-\cos\theta}{2}\\ &\cos^2\frac{\theta}{2}=\frac{1+\cos\theta}{2}\\ &\tan^2\frac{\theta}{2}=\frac{1-\cos\theta}{1+\cos\theta}\\ \end{split} \end{equation} $$

3倍角の公式

$$ \begin{equation} \begin{split} &\sin3\theta=3\sin\theta-4\sin^3\theta\\ &\cos3\theta=3\cos\theta+4\cos^3\theta\\ \end{split} \end{equation} $$

2倍角、半角の公式のスペック

使用頻度

低

1

2

3

高
導出難易度

易しい

1

2

3

難しい
暗記/理解

暗記重視

1

2

3

理解重視

★公式の解説

“〇倍角の公式”攻略の結論

2倍角の公式、半角の公式などめちゃくちゃ重要でしっかり覚えるようにと教え込まれたと思いますが、結論これらの公式は全部覚えなくてokです。理由は、すべて加法定理から導き出せるからです。

2倍角の公式の攻略法

2倍角の公式

例として、
$$
\begin{equation}
\begin{split}
\cos2\theta&=2\cos^2\theta-1\quad\cdots①\\
&=1-2\sin^2\theta\quad\cdots②
\end{split}
\end{equation}
$$
の導出方法を解説します。ずばり使う公式は「加法定理」のみです。加法定理の覚え方はpart1の記事で解説しているので、詳しくはそちらを確認しておきましょう。

■2倍角の公式導出方法（$\small \cos2\theta$編）
$\small 2\theta=\theta+\theta$として加法定理を用いると、
$$
\begin{equation}
\begin{split}
\cos\color{red}{2\theta}&=\cos(\color{red}{\theta+\theta})\\
&=\cos\theta\cos\theta-\sin\theta\sin\theta\\
&=\cos^2\theta-\sin^2\theta\\
\end{split}
\end{equation}
$$
①$\small \sin^2\theta=1-\cos^2\theta$で$\small \sin\theta$を消去すると…
$$
\begin{equation}
\begin{split}
(\text{与式})&=\cos^2\theta-\color{blue}{\sin^2\theta}\\
&=\cos^2\theta-\color{blue}{(1-\cos^2\theta)}\\
&=2\cos^2\theta-1\quad\cdots①\\
\end{split}
\end{equation}
$$
②$\small \cos^2\theta=1-\sin^2\theta$で$\small \cos\theta$を消去すると…
$$
\begin{equation}
\begin{split}
(\text{与式})&=\color{blue}{\cos^2\theta}-\sin^2\theta\\
&=\color{blue}{(1-\sin^2\theta)}-\sin^2\theta\\
&=1-2\sin^2\theta\quad\cdots②\\
\end{split}
\end{equation}
$$

こんな感じですぐに導けるので、加法定理だけ覚えておけば大丈夫です。
$\small \sin2\theta$と$\small \tan2\theta$も$\small 2\theta=\theta+\theta$として加法定理を使えば同じように計算できるので、試してみましょう！

半角の公式の攻略法

半角の公式

これは、2倍角の公式と同じこと言っているだけなので覚える価値”ゼロ”です。
そもそも、しれっと左辺が2乗（$\small \sin^\color{red}2\frac{\theta}{2}$など）になっているという訳の分からない公式。無いならないで無理やり作らないで…。

話を戻して、どうして半角の公式を覚えなくてよいのかですが、例えば2倍角の公式
$$\cos2\theta=2\cos^2\theta-1$$
で、$\small \theta=\frac{\alpha}{2}$と置き換えると
$$
\begin{equation}
\begin{split}
&\quad\cos\left(2\cdot\color{red}{\frac{\alpha}{2}}\right)=2\cos^2\color{red}{\frac{\alpha}{2}}-1\\
\Leftrightarrow &\quad\cos\alpha=2\cos^2\frac{\alpha}{2}-1\\
\Leftrightarrow &\quad\cos\alpha+1=2\cos^2\frac{\alpha}{2}\\
\Leftrightarrow &\quad\frac{\cos\alpha+1}{2}=\cos^2\frac{\alpha}{2}\\
\end{split}
\end{equation}
$$

皆さんお気づきの通り、この式は右辺と左辺が逆ですが、半角の公式の$\small \cos^2\frac{\theta}{2}$の公式です。

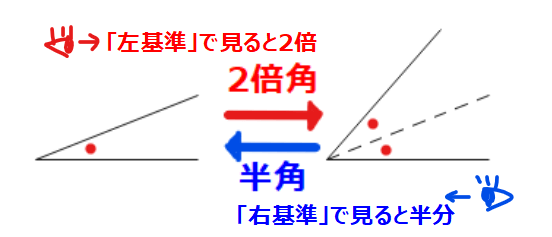
今回の式変形は、元を辿れば2倍角の公式なので、「半角の公式は2倍角の公式と同じことを言っている」ことになります。これは相対的な話で、元の角度と2倍した角度があったときに、元の角度基準で見れば当然2倍ですが、2倍の角度を基準に元の角度を見ると半分に見えるからです。あまりピンと来ない人は、「人から見てアリは小さいけど、アリから見て人は大きい」的なことを言っていると思っておきましょう。

$\small \sin^2\frac{\theta}{2}$も$\small \cos2\theta=1-2\sin^2\theta$の公式を使って同じような置き換えをすれば出てくるので確かめてみるとよいと思います。$\small \tan^2\frac{\theta}{2}$は、あまり使う機会はないですが
$$
\begin{equation}
\begin{split}
\tan^2\frac{\theta}{2}&=\frac{\sin^2\frac{\theta}{2}}{\cos^2\frac{\theta}{2}}\\
&=\dfrac{\frac{1-\cos\theta}{2}}{\frac{1+\cos\theta}{2}}\\
&=\frac{1-\cos\theta}{1+\cos\theta}\\
\end{split}
\end{equation}
$$

で求まります。

★豆知識
実際の使用場面としては、数Ⅲの積分でよく使います。ここでは詳細触れませんが、$\small \cos^2\theta$はそのままだと積分ができないので、半角の公式を使って
$$\int \cos^2\theta dx=\int \frac{1+\cos2\theta}{2}dx$$
として計算を進めたりします。この時に式変形で使った公式が
$$\cos^2\theta=\frac{1+\cos\theta}{2}$$
で、半角の公式と2倍角の公式の中間みたいな感じで使っています。
このことからもわかるように、公式自体を覚えるよりも2倍角の公式を式変形していろいろな形に応用できるようにすることが大切です。

3倍角の公式

3倍角の公式

$$ \begin{equation} \begin{split} &\sin3\theta=3\sin\theta-4\sin^3\theta\\ &\cos3\theta=3\cos\theta+4\cos^3\theta\\ \end{split} \end{equation} $$

3倍角の公式は、使用頻度もほぼないので導出方法だけ覚えておけばよいかなと思います。
導出方法も2倍角の公式と同じで、加法定理を使えばokです。

■$\small \sin3\theta$の公式導出方法
$$
\begin{equation}
\begin{split}
\sin\color{red}{3\theta}&=\sin\color{red}{(\theta+2\theta)}\\
&=\sin\theta\color{blue}{\cos2\theta}+\cos\theta\color{blue}{\sin2\theta}\\
&=\sin\theta\color{blue}{(1-2\sin^2\theta)}+\cos\theta\cdot\color{blue}{(2\sin\theta\cos\theta)}\\
&=\sin\theta-2\sin^3\theta+2\sin\theta\color{blue}{\cos^2\theta}\\
&=\sin\theta-2\sin^3\theta+2\sin\theta\color{blue}{(1-\sin^2\theta)}\\
&=\sin\theta-2\sin^3\theta+2\sin\theta-2\sin^3\theta\\
&=3\sin\theta-4\sin^3\theta\\
\end{split}
\end{equation}
$$

$\small \cos3\theta$も同様に導出できるので、試してみましょう。

まとめ

今回は、三角関数頻出の2倍角/半角/3倍角の公式の攻略法について解説しました。結論、2倍角/半角/3倍角の公式は暗記不要で、加法定理からすべて導出できることを解説しました。

でも、「本当に全部暗記しなくていいの？」、「全部導出していたら試験時間内に問題が解き終わらなくなるんじゃないか？」という疑念の声もあるかと思います。

この質問に関しては、「暗記できるなら暗記すればいい」というのが個人的な答えです。勘違いしてほしくないのは、「暗記不要≠暗記してはいけない」ではないということ。
もちろん、暗記できるのであれば導出しなくてよい分、問題を考えることに時間を割ける、導出による頭のキャパを使わなくてよいなどメリットもあります。一方で、暗記だけでは、ド忘れしたときに詰んでしまう、応用力に欠けるといったデメリットもあります。
なので、個人的には、「公式暗記はしつつも、忘れたとき用に導出方法も押さえておく」というのが完璧だと思います。皆さんもこんな塩梅を目指して頑張っていきましょう！

本日はここまでです。お疲れさまでした！