【三角関数を含む不等式】置き換え・場合分けのコツと単位円を使った解の範囲の求め方を分かりやすく解説

こんにちは。管理人のhiroemonです。

本記事では、三角関数を含む不等式の中でも、2次不等式を利用した問題の解き方を徹底解説していきます。「単位円を使った解き方がよくわからない…」、「出てきた答えの範囲をどうすればよいかわからない（合計範囲？共通範囲？）…」という悩みを抱えている人でもわかりやすいように丁寧に解説しているので、ぜひ最後まで読んでみてください！

今回解く問題では、2次不等式の解き方は理解できている前提での解説になりますので、もし「2次不等式ってどう解くんだっけ？」と不安になった人は、初めに2次不等式の解き方を読んでからこの記事の問題を解くのがよいかと思います。では早速始めましょう！

　本記事はこんな人におすすめ

単位円を使った解き方がよくわからない…
出てきた答えの範囲をどうすればよいかわからない（合計範囲？共通範囲？）…
三角関数を含む不等式の問題が解きたい！

　本記事で扱う問題

問題

$\small 0 \leq \theta < 2\pi$のとき、以下の不等式を解け。
(1) $\small 2 \sin^2 \theta +5\cos \theta \ge 4 $
(2) $\small \sin 2\theta > \cos\theta$

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

1.予備知識
1. 1.1 知っておきたい公式
2. 1.2 知っておきたい単位円の性質
2.三角関数×2次関数の問題＆解説
3.まとめ

1.予備知識

1.1 知っておきたい公式

三角関数にはいろいろな公式がありますが、三角関数と2次関数がコラボした不等式を解くときに必要な公式は、実は以下の1つしかありません！

■2次関数を含む三角関数を解く上で必要な公式
$$\sin^2\theta + \cos^2 \theta =1$$

三角関数には、3つの登場人物$\small \sin\theta,\cos\theta,\tan\theta$がいますが、2次関数として解くためには1種類に統一してあげる必要があります。そして、ほとんどの問題では$\small \tan\theta$は出てこないので、$\small \sin\theta$と$\small \cos\theta$を変換するために、「$\small \sin^2\theta+\cos^2\theta=1$」の公式を使います。

1.2 知っておきたい単位円の性質

三角不等式を解く上で、単位円の性質は絶対に押させておく必要があるので、ここで改めて確認しておきましょう。

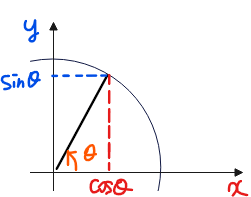
■単位円の特徴

単位円上では、$\small \cos\theta$=$\small x$座標。
単位円上では、$\small \sin\theta$=$\small y$座標。

2.三角関数×2次関数の問題＆解説

★基本問題

基本問題

$\small 0 \leq \theta < 2\pi$のとき、以下の不等式を解け。
(1) $\small 2 \sin^2 \theta +5\cos \theta \ge 4 $

★解法と解説

■解き方の流れ

STEP1

文字種の統一

→$\small \sin\theta$または$\small \cos\theta$だけに統一する。

STEP2

範囲の確認

→$\small \theta$の範囲から$\small \sin\theta$または$\small \cos\theta$の範囲を求める。

STEP3

2次不等式への置き換え

→$\small \sin\theta =x$などと置き換えて、step2で求めた範囲を踏まえて2次不等式として解く。

STEP4

三角不等式の処理

→step3で解いた答えを三角関数の不等式として解く。

解説

手順が盛りだくさんですが、一つずつ理解してしまえばそれほど難しくはないので、stepごとに見ていきましょう！

step1：文字種の統一

今回の問題では、$\small 2 \sin^2 \theta +5\cos \theta \ge 4 $の式の中に、$\small \sin\theta$と$\small \cos\theta$が含まれているので、$\small \sin^2\theta + \cos^2 \theta =1$の公式を使って、

$$
\begin{equation}
\begin{split}
&2 \sin^2 \theta +5\cos \theta \ge 4 \\
&2(1-\cos^2\theta)+5\cos \theta \ge 4 \\
&-2\cos^2\theta+5\cos \theta -2 \ge 0 \\
&2\cos^2\theta-5\cos \theta +2 \leq 0 \quad \cdots (*)\\
\end{split}
\end{equation}
$$

step2：範囲の確認

すぐに$\small (*)$の2次不等式を解きたくなる気持ちを抑えて、$\cos\theta$がとり得る値の範囲を求めておきます。これを忘れる人が多いのでしっかり覚えておきましょう！

$\small 0 \leq \theta < 2\pi$とあるので、$\small -1 \leq \cos\theta \leq 1 \cdots ①$ですね。

step3：2次不等式への置き換え

では、お待ちかねの$\small (*)$を解いていきます。「文字を置き換えなくてもできるよ！」という人はそのままでもokですが、ここでは$\small \cos\theta = x$と置き換えることにします。

①から、$\small -1 \leq x \leq 1\cdots①’$.
$$
\begin{equation}
\begin{split}
&2\cos^2\theta-5\cos \theta +2 \leq 0\\
&\Rightarrow 2x^2-5x+2 \leq 0\\
&\space \quad (2x-1)(x-2)\leq 0\\
\end{split}
\end{equation}
$$
$$\frac{1}{2} \leq x \leq 2\cdots ②$$

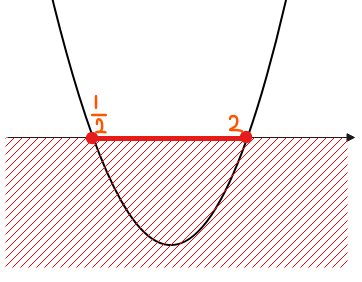
①’と②の共通範囲をとって、$\small \frac{1}{2} \leq x \leq 1$。 ※まだ答えではないので注意！

step4：三角不等式の処理

もともと、$\small x$は$\small \cos\theta$のことだったので、戻してあげると

$$\frac{1}{2} \leq \cos\theta \leq 1$$

あとは、この三角不等式を解けば答えになります。

三角不等式を解くときには必ず単位円を描いて考えるようにしましょう。

■解法のポイント
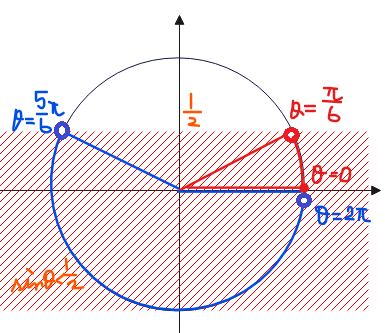
今回の三角不等式は、「$\small \cos\theta$ が$\small \frac{1}{2}$～1となる」＝「単位円上の$\small x$座標が$\small \frac{1}{2}$～1となる角度を求める」ことができればOK！

■$\small \cos \theta$が$\small \frac{1}{2}$になる角度$\small \theta$の求め方

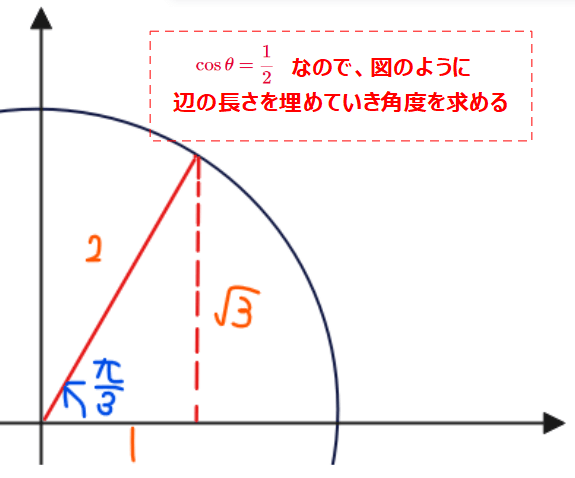
■$\small \frac{1}{2} \leq \cos \theta \leq 1$の範囲

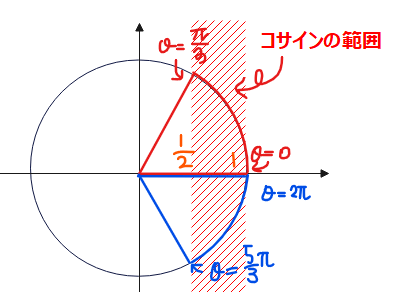
不等号にイコールが入るかだけ注意して、単位円で求めた範囲を不等号で表せば答えになります。

（解答）
$$0 \leq \theta \leq \frac{\pi}{3},\quad \frac{5}{3}\pi \leq \theta < 2\pi \quad \cdots (答)$$

★応用問題

応用問題

$\small 0 \leq \theta < 2\pi$のとき、以下の不等式を解け。
(2) $\small \sin 2\theta > \cos\theta$

★解法＆解説

解説

解き方は先程とほぼ同じですが、ひとひねりされているので、復習もかねて解けるか確認してみましょう！

step1：文字種の統一

はじめは文字種の統一ですが、今回は実は1種類に統一することはできません。ですが、2次不等式みたいに因数分解できれば解くことができるので、その形を目指すべく2倍角の公式を使っていきます。

■2倍角の公式
$$\sin 2\theta =2\sin \theta \cos \theta$$

2倍角の公式より

$$
\begin{equation}
\begin{split}
&\sin 2\theta > \cos\theta\\
&2\sin \theta \cos \theta > \cos\theta\\
&2\sin \theta \cos \theta -\cos\theta > 0\\
&\cos \theta (2\sin \theta – 1) > 0\\
\end{split}
\end{equation}
$$

step2：範囲の確認

$\small 0 \leq \theta < 2\pi$なので、$\small -1 \leq \sin \theta \leq 1$、$\small -1 \leq \cos \theta \leq 1$になります。

step3：不等式の処理

解くべき不等式$\small \cos \theta (2\sin \theta – 1) > 0$は、「掛け算が正になる」という式ですので、2つの掛け合わせる値の符号について以下のことが分かります。

■AB>0の解き方
A、Bは以下(1)、(2)のいずれかを満たす。
(1)$\small \mathrm{A}>0$ かつ $\small \mathrm{B}>0$
(2)$\small \mathrm{A}<0$ かつ $\small \mathrm{B}<0$

※掛け算が正ということは、「$\small (+)×(+)$」または「$\small (-)×(-)$」ということ

よって、

[1]$\small \cos \theta > 0$ かつ $\small 2\sin \theta – 1>0$の場合
[2]$\small \cos \theta < 0$ かつ $\small 2\sin \theta – 1<0$の場合
のいずれかを満たす。

を解いていけばよいことになります。

step4：三角不等式の処理

[1]$\small \cos \theta > 0$ かつ $\small 2\sin \theta – 1>0$の場合

$\small 2\sin \theta – 1>0$は、式変形しておくと$\small \sin\theta >\frac{1}{2}$.

■$\small \cos \theta > 0$

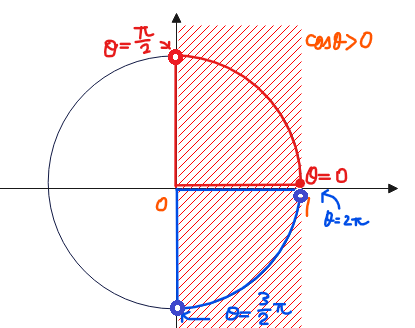
$$0 \leq \theta < \frac{\pi}{2}, \quad \frac{3}{2}\pi < \theta < 2\pi \quad \cdots①$$

■$\small \sin\theta >\frac{1}{2}$

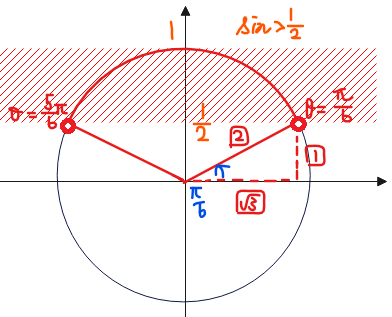
$$\frac{\pi}{6} < \theta < \frac{5}{6}\pi\quad \cdots②$$

「$\small \cos \theta > 0$」かつ「$\small 2\sin \theta – 1>0$」は、①と②の共通範囲（AND条件）なので、

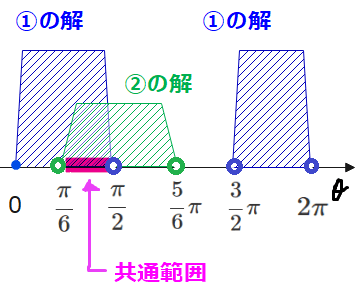
$$\frac{\pi}{6} < \theta < \frac{\pi}{2} \quad \cdots ③$$

[2]$\small \cos \theta < 0$ かつ $\small 2\sin \theta – 1<0$の場合

こちらも同様に解いていきます（$\small 2\sin \theta – 1<0$は、式変形しておくと$\small \sin\theta <\frac{1}{2}$）。

■$\small \cos \theta < 0$

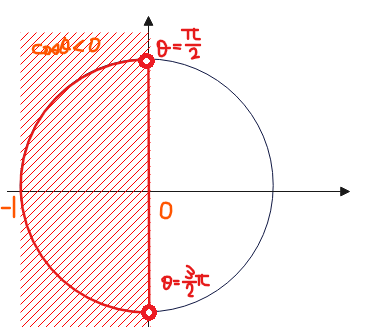
$$\frac{\pi}{2} < \theta < \frac{3}{2}\pi \quad \cdots④$$

■$\small \sin\theta <\frac{1}{2}$

$$0 \leq \theta < \frac{\pi}{6}, \quad \frac{5}{6}\pi < \theta < 2\pi \quad \cdots⑤$$

④、⑤の共通範囲から、

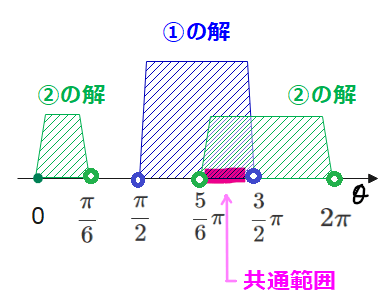
$$\frac{5}{6}\pi < \theta < \frac{3}{2}\pi \quad \cdots ⑥$$

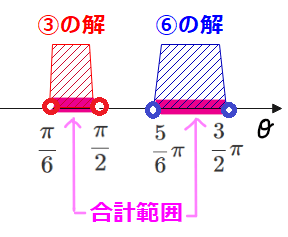
最後に、[1]で求めた③と[2]で求めた⑥は、「いずれかを満たす」だったので、合計範囲を求めることで答えになります。

(解答)
$$
\begin{equation}
\begin{split}
&\frac{\pi}{6} < \theta < \frac{\pi}{2},\\
&\frac{5}{6}\pi < \theta < \frac{3}{2}\pi \quad \cdots (答)
\end{split}
\end{equation}
$$