今回は、三角関数の不等式の中でも少し応用的な問題である角度を置き換えする問題や角度の範囲が\(\small 0≦\theta <2\pi\)ではない問題、三角関数の両端が不等号で挟まれている問題の解き方について徹底解説していきます。そのため、基本的な三角関数の不等式を解く問題の解き方を確認したい方は、【三角関数を含む不等式】単位円を利用した解の範囲の求め方(基礎問題)の記事で詳しく解説しているので、確認してみてください!
本記事で扱う問題は、基礎をしっかり理解していれば変数の置き換えや範囲変更の手順が加わるだけで大きな考え方は基本問題と変わらないのですが、基礎的な考え方を十分に理解せずに暗記しているとかなり混乱してしまうことになるため、差がつきやすい分野になっています。なので、不明点があれば冒頭の解説記事で扱っている全12パターンの基礎問題に立ち返って考え方を再確認するとよいでしょう。
では早速今回の問題の解説を始めていきたいと思います!
- 三角関数を含む不等式の応用問題(変数の置き換え、範囲変更)が解けるようになりたい人
- 応用的な問題での単位円の活用方法を知りたい人
- 定期テスト対策、大学受験対策がしたい人
【問題&解説】三角関数の不等式(応用問題)
【問題1】角度が \(\small p\theta+q\) 型の問題(難易度:★★☆)
\(\small 0≦\theta < 2\pi\)のとき、次の不等式を解け。
(1)\(\small \displaystyle \sin\left(\theta-\frac{\pi}{4}\right) ≧\frac{1}{2}\)
(2)\(\small \displaystyle 2\cos\left(2\theta+\frac{\pi}{6}\right) >\sqrt{3}\)
(3)\(\small \displaystyle \sqrt{3}\tan\left(\theta-\frac{\pi}{3}\right) ≦1\)
・STEP1:角度部分を\(\small p\theta + q =t\)とおき、基本形(12パターン)に帰着させる。
*基本形(12パターン)とその解き方は本記事参照。
・STEP2:置き換えた 文字 \(\small t\) の範囲を確認
・STEP3:STEP2で確認した範囲内で、三角関数の不等式を解く。
・STEP4:STEP3で求めた解を変換前の文字 \(\small \theta \) に戻す。
角度の中身を \(\small \displaystyle \theta -\frac{\pi}{4} = t\)とおく。
変数の置き換えをしたので、問題の条件 \(\small 0≦\theta<2\pi\) で与えられている\(\small \theta\)の範囲に対応して \(\small t\)の範囲を確認しておく。
\begin{split}
\small 0 &\small ≦\theta<2\pi\\
\small \Leftrightarrow \space \color{#ef5350}{-\frac{\pi}{4}} &\small ≦\theta\color{#ef5350}{-\frac{\pi}{4}}<2\pi\color{#ef5350}{-\frac{\pi}{4}}\\
\small \Leftrightarrow \space -\frac{\pi}{4} &\small ≦t <2\pi-\frac{\pi}{4} \space \cdots ①\\
\end{split}
●補足
①の不等式の一番右端は、\(\small \displaystyle 2\pi – \frac{\pi}{4}=\frac{7}{4}\pi\)と計算してもよいが、あとで単位円を描く際に \(\small \displaystyle \frac{7}{4}\pi\)の位置が分かりにくくなるため、あえて計算せずにそのままにしている。
変数変換した不等式は \(\small \displaystyle \sin t ≧\frac{1}{2}\)となるため、これは三角関数の不等式の基本形に帰着する。ただし、角度 \(\small t\) の範囲が\(\small 0~2\pi\)ではなく、①の範囲であることに注意が必要。
すなわち、下図のような単位円で考えると、\(\small \displaystyle t=-\pi/4\)からスタートし、\(\small t = 2\pi-\pi/4\)まで一周する範囲で不等式\(\small y≧1/2\)を満たす範囲(紫色領域)を通過する単位円上の部分を確認すればよい。
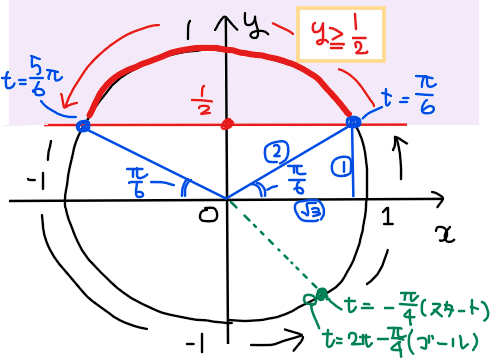
よって、図の赤線部分が解の範囲となるので、端点の角度を求めることで \(\small \displaystyle \frac{\pi}{6}≦t≦\frac{5}{6}\pi\)を得る(まだ答えじゃないので注意!!)。
最後に変数変換した文字をもとの \(\small \theta\)に戻してあげると
\begin{split}
&\small \frac{\pi}{6}≦t≦\frac{5}{6}\pi\\
\small \Leftrightarrow \space &\small \frac{\pi}{6} ≦\color{#ef5350}{\theta-\frac{\pi}{4}}≦\frac{5}{6}\pi\\
\small \Leftrightarrow \space &\small \color{red}{\frac{5}{12}\pi ≦\theta ≦\frac{13}{12}\pi \space \cdots 【答】}\\
\end{split}
問題文の不等式を式変形して
\begin{split}
&\small \cos\left(2\theta +\frac{\pi}{6}\right)>\frac{\sqrt{3}}{2}\\
\end{split}
の形にしておく。
角度部分を \(\small \displaystyle 2\theta +\frac{\pi}{6}=t\) とおくと、\(\small t\)の範囲は
\begin{split}
&\small 0≦\theta <2\pi\\
\small \Leftrightarrow \space &\small 0≦\color{#ef5350}{2}\theta <\color{#ef5350}4\pi\\
\small \Leftrightarrow \space &\small \color{#ef5350}{\frac{\pi}{6}} ≦2\theta \small \color{#ef5350}{+\frac{\pi}{6}} <4\pi \color{#ef5350}{+\frac{\pi}{6}} \\
\small \Leftrightarrow \space &\small \frac{\pi}{6} ≦ t <4\pi +\frac{\pi}{6} \\
\end{split}
単位円を考えると、今回は\(\small t = \pi/6\)からスタートし、\(\small t = 4\pi +\pi/6\)がゴールとなるが、\(\small 4\pi = 2\pi \times 2\)なので単位円上を2周することに注意する。
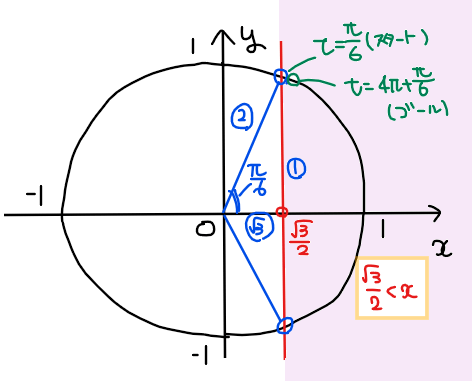
●補足
スタート地点が\(\small \displaystyle t = \frac{\pi}{6}\)となっているため、\(\small \displaystyle \cos t = \frac{\sqrt{3}}{2}\)の解となる \(\small t\)の値との位置関係に注意して単位円上に図示するようにする。本問ではたまたま一致している。
よって、解の範囲は下図の赤色部分(1周目)と緑色部分(2周目)になる[*1]ので
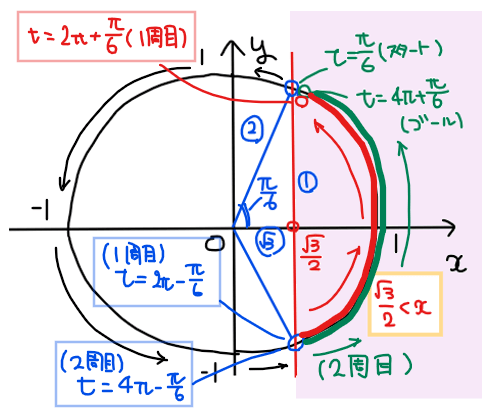
\begin{split}
&\small \displaystyle \color{red}{2\pi-\frac{\pi}{6}< t < 2\pi +\frac{\pi}{6}}, \space \color{green}{4\pi-\frac{\pi}{6}< t < 4\pi +\frac{\pi}{6}} \quad [*2]\\
\end{split}
が不等式の解の範囲になる。
*1:【補足】端点の \(\small t\) の値について
2周以上になると角度計算が分かりにくくなるが、たとえば\(\small t =2\pi -\pi/6\)であれば、1周目は\(\small 2\pi\)から\(\small \pi/6\)だけ時計回りに戻った点、2周目は\(\small 4\pi\)から\(\small \pi/6\)だけ時計回りに戻った点(または、1周目の\(\small t =2\pi -\pi/6\)に\(\small +2\pi\)(+1周)した点)と考えると求めやすい。
*2:【補足】不等式の分数計算について
不等式 \(\small t\)の範囲は計算してもよいが、分数計算のため面倒になりがち(+計算ミスの温床になりがち…)であり、このあとに変数を\(\small \theta \)に戻す際に\(\small \pi/6\)が打ち消す部分もあるので、一旦はあえて計算せずに残しておく方が計算が楽になることが多い。
よって、文字 \(\small t\)をもとの文字 \(\small \theta \)に戻してあげれば答えになる。
\begin{split}
&\small \color{red}{2\pi-\frac{\pi}{6}< t < 2\pi +\frac{\pi}{6}}\\
\small \Leftrightarrow \space &\small 2\pi-\frac{\pi}{6}< 2\theta+\frac{\pi}{6} < 2\pi +\frac{\pi}{6}\\
\small \Leftrightarrow \space &\small 2\pi-\frac{\pi}{3}< 2\theta < 2\pi\\
\small \Leftrightarrow \space &\small \frac{5}{6}\pi< \theta < \pi\\
\end{split}
\begin{split}
&\small \color{green}{4\pi-\frac{\pi}{6}< t < 4\pi +\frac{\pi}{6}}\\
\small \Leftrightarrow \space &\small 4\pi-\frac{\pi}{6}< 2\theta+\frac{\pi}{6} < 4\pi +\frac{\pi}{6}\\
\small \Leftrightarrow \space &\small \frac{11}{6}\pi< \theta < 2\pi\\
\end{split}
ゆえに、\(\small \displaystyle \frac{5}{6}\pi< \theta < \pi, \space \frac{11}{6}\pi< \theta < 2\pi\)…【答】.
\begin{split}
&\small \displaystyle \sqrt{3}\tan\left(\theta-\frac{\pi}{3}\right) ≦1\\
\small \Leftrightarrow \space &\small \displaystyle \tan\left(\theta-\frac{\pi}{3}\right) ≦\frac{1}{\sqrt{3}} \space \cdots ①\\
\end{split}
角度部分を \(\small \displaystyle \theta -\frac{\pi}{3}=t\) とおくと、\(\small t\)の範囲は
\begin{split}
\small 0 &\small ≦ \theta <2\pi\\
\small \Leftrightarrow \space \color{#ef5350}{-\frac{\pi}{3}} &\small ≦\theta \color{#ef5350}{-\frac{\pi}{3}} <2\pi \color{#ef5350}{-\frac{\pi}{3}}\\
\small \Leftrightarrow \space -\frac{\pi}{3} &\small ≦t <2\pi -\frac{\pi}{3}\\
\end{split}
スタート地点である\(\small t=-\pi/3\)からゴール地点の\(\small t =2\pi-\pi/3\)の1周分(ちょうど \(\small 2\pi\) だけ移動しているので)の範囲内で、①の不等式の範囲に該当する単位円上の部分を図示すると下図の通り。
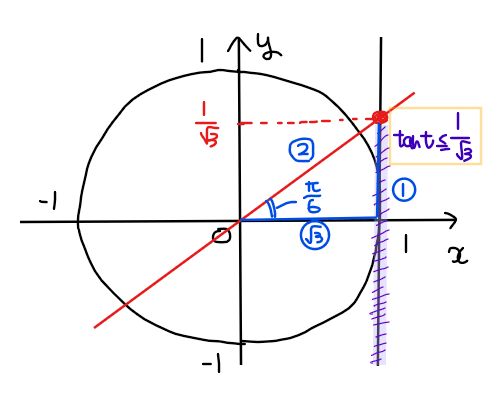
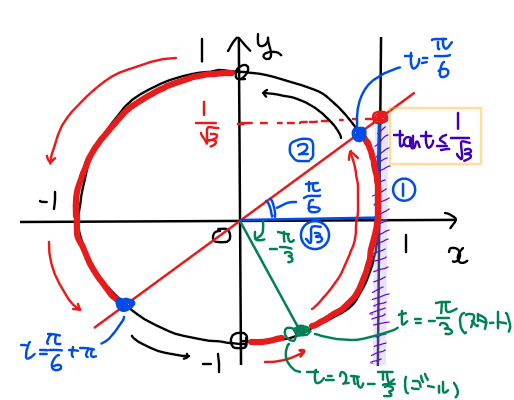
スタート位置との兼ね合いで今回は解の範囲が3つ範囲に分かれている。
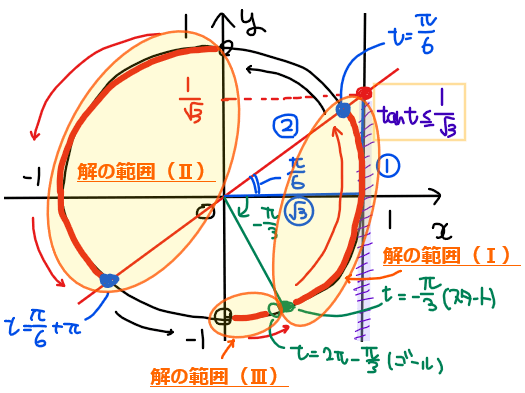
赤色部分の3つの範囲を不等式で表すと
\begin{split}
&\small \displaystyle \color{green}{-\frac{\pi}{3}}≦ t ≦ \color{blue}{\frac{\pi}{6}}, \\
&\small \displaystyle \frac{\pi}{2}< t ≦ \color{blue}{\pi +\frac{\pi}{6}}, \\
&\small \displaystyle \frac{3}{2}\pi< t < \color{green}{2\pi -\frac{\pi}{3}} \quad [*3]\\
\end{split}
*3:【補足】端点の不等号について
\(\small \tan t\)が定義されていない \(\small \displaystyle \frac{\pi}{2}\)や\(\small \displaystyle \frac{3}{2}\pi\)、ゴール地点である \(\small \displaystyle t = 2\pi -\frac{\pi}{3}\)はイコールを含まない不等号(白丸)になることに注意しよう。
最後に、置き換えた文字 \(\small t\)を \(\small \theta \) に戻すと
\begin{split}
\small -\frac{\pi}{3}≦ &\small \color{#ef5350}t ≦ \frac{\pi}{6}\\
\small \Leftrightarrow \space -\frac{\pi}{3}≦ &\small \color{#ef5350}{\theta -\frac{\pi}{3}} ≦ \frac{\pi}{6}\\
\small \Leftrightarrow \space 0≦ &\small \theta≦ \frac{\pi}{2}\\
\end{split}
\begin{split}
\small \frac{\pi}{2}< &\small \color{#ef5350}t ≦ \pi +\frac{\pi}{6}\\
\small \Leftrightarrow \space \frac{\pi}{2}< &\small \color{#ef5350}{\theta -\frac{\pi}{3}}≦ \pi +\frac{\pi}{6}\\
\small \Leftrightarrow \space \frac{5}{6}\pi &\small < \theta ≦ \frac{3}{2}\pi\\
\end{split}
\begin{split}
\small \frac{3}{2}\pi<&\small \color{#ef5350}t < 2\pi -\frac{\pi}{3}\\
\small \Leftrightarrow \space \frac{3}{2}\pi<&\small \color{#ef5350}{\theta -\frac{\pi}{3}} < 2\pi -\frac{\pi}{3}\\
\small \Leftrightarrow \space \frac{11}{6}\pi &\small < \theta< 2\pi\\
\end{split}
よって、\(\small \displaystyle 0≦ \theta≦ \frac{\pi}{2}\), \(\small \displaystyle \frac{5}{6}\pi < \theta ≦ \frac{3}{2}\pi\), \(\small \displaystyle \frac{11}{6}\pi < \theta< 2\pi\)…【答】.
【問題2】角度の範囲が\(\small 0≦\theta <2\pi\)ではない問題(難易度:★☆☆)
(1)\(\small -\pi≦\theta < \pi\)のとき、不等式 \(\small \displaystyle \cos\theta > \frac{1}{2}\) を解け。
(2)\(\small 0≦\theta ≦ \pi\)のとき、不等式 \(\small \displaystyle \cos\theta ≦ -\frac{1}{\sqrt{2}}\) を解け。
単位円上で \(\small \displaystyle x>\frac{1}{2}\)の範囲を図示すると下図のようになる。
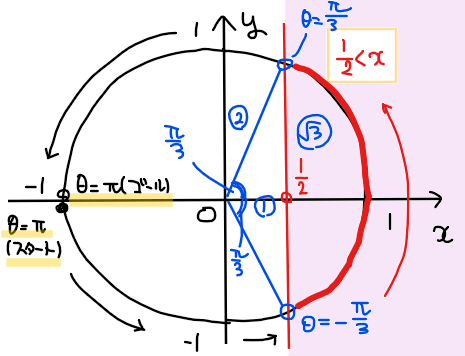
本問では、考えるべき角度の範囲が \(\small \theta = -\pi\)をスタート地点として、\(\small \theta =\pi\)まで一周する範囲であることから、該当する角度の範囲は、\(\small \displaystyle -\frac{\pi}{3}< \theta < \frac{\pi}{3}\)…【答】.
●参考
考える角度の範囲が \(\small 0≦\theta < 2\pi\)であれば、下図のようにスタート地点が不等式の範囲の中間に位置しているため、赤色部分と緑色部分の2箇所の範囲に解が分かれる。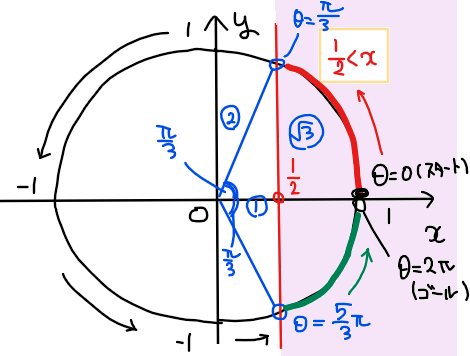
このように角度の範囲は答えに大きく影響するため、しっかりと確認すること。
単位円上で \(\small \displaystyle x≦-\frac{1}{\sqrt{2}}\)の範囲を図示すると下図のようになる。
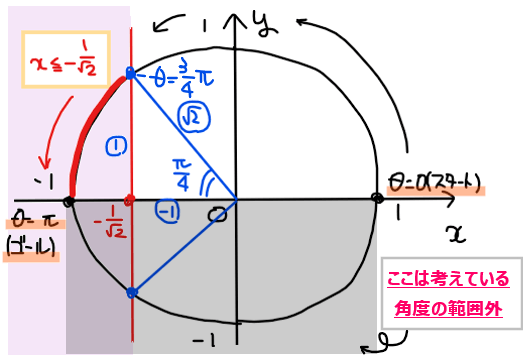
今回考えている角度の範囲としては \(\small 0≦\theta ≦\pi\)(単位円の上半分)なので、不等式を満たすような角度の範囲は、\(\small \displaystyle \frac{3}{4}\pi≦\theta ≦\pi\)…【答】.
●補足
\(\small \displaystyle \pi≦\theta ≦\frac{5}{4}\pi\)の範囲も不等式を満たすが、\(\small 0≦\theta≦\pi\)の範囲外となるため、今回は解の範囲には含まれない点に注意する。
【問題3】不等号で挟まれた三角関数の不等式(難易度:★☆☆)
\(\small 0≦\theta <2\pi\)のとき、次の不等式を解け。
(1)\(\small \displaystyle \frac{1}{2}≦\sin\theta≦\frac{\sqrt{3}}{2}\)
(2)\(\small \displaystyle -\frac{1}{\sqrt{2}}≦\cos\theta < \frac{1}{2} \)
問題の不等式 \(\small \displaystyle \frac{1}{2}≦y≦\frac{\sqrt{3}}{2}\) が表す範囲を単位円上に図示すると下図の紫色領域の範囲になる。
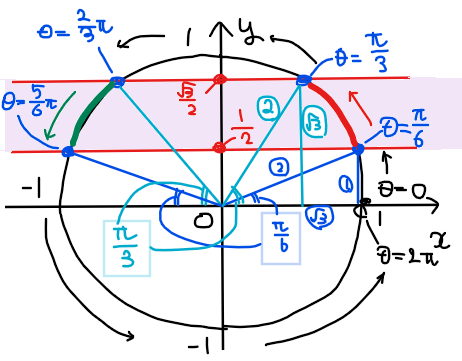
よって、求める角度の範囲は、\(\small \displaystyle \frac{\pi}{6}≦\theta ≦\frac{\pi}{3}\), \(\small \displaystyle \frac{2}{3}\pi≦\theta ≦\frac{5}{6}\pi\)…【答】.
問題の不等式 \(\small \displaystyle -\frac{1}{\sqrt{2}}≦x < \frac{1}{2}\) が表す範囲を単位円上に図示すると下図の紫色領域の範囲になる。
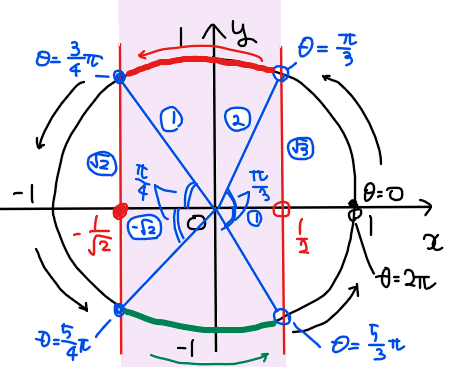
よって、求める角度の範囲は、\(\small \displaystyle \frac{\pi}{3}<\theta ≦\frac{3}{4}\pi\), \(\small \displaystyle \frac{5}{4}\pi≦\theta <\frac{5}{3}\pi\)…【答】.
本記事のまとめ
今回は三角関数の不等式の応用問題として、角度が \(\small p\theta + q\)型の問題、角度の範囲が \(\small 0 ≦\theta<2\pi \) ではない問題、不等号で挟まれた三角関数の不等式の問題について解説していきました。いずれの問題であっても、三角関数の不等式の基本形である『【三角関数】 【不等号】 【値】』の形に帰着させて解くという方針は共通のため、それほど難しくはなかったかのではないかなと思います。
入試問題では、単純な暗記で解ける問題だけでは『理解している人』と『ただ解き方を暗記している人』を見分けることができず点数の差も生まれにくいため、しっかりと考え方を理解できているかという応用力を問う問題が頻出します。今回の問題も、考え方を理解していれば多少問題の見た目が変わっても解くことができるはずなので、解き方を覚えるのではなく、考え方を理解することを意識して演習することをおすすめします。
では、本日はここまでです。お疲れさまでした!








コメント