本記事では、角度の範囲が指定された三角関数の最大値・最小値の求め方を、基礎から入試レベルの応用まで順を追って解説します。
三角関数の問題では一般に、角度の範囲は\(\small 0≦\theta <2\pi\)で指定されていることが多いですが、入試問題では\(\small 0≦\theta≦\pi\)や\(\small -\pi≦\theta ≦\pi\)など角度の範囲が一部に限定された「範囲あり」の問題が頻出します。
このような範囲制限があると、最大値・最小値の求め方が一気に難しく感じる人も多いはずです。そこで本記事では、角度の範囲が指定されている場合の三角関数の最大値、最小値を求める問題について、三角関数の合成や単位円を使った根本的な考え方をわかりやすく解説していきます。本記事の解説を通して基本的な考え方の流れと実践的な解法を身に着けていきましょう!
- 角度の範囲が指定された三角関数の最大値・最小値の求め方を基礎から理解したい人
- 単位円を使った最大最小の判断方法や、合成・置き換えの流れを確実に身につけたい人
- 定期テスト・共通テスト・大学入試レベルの三角関数問題をスムーズに解けるようになりたい人
【問題&解説】範囲指定がある三角関数の最大・最小
【問題1】範囲指定がある三角関数の最大最小【基礎編】(難易度:★☆☆)
\(\small \displaystyle -\frac{\pi}{3}≦\theta≦\frac{2}{3}\pi\)のとき、\(\small f(\theta)= 2\sin \theta\)の最大値、最小値を求めよ。
2次関数関数の最大・最小を求める問題では、グラフを書いて求めていたので、同じように考えると三角関数の最大・最小もグラフを書いて求めたくなりますが、三角関数のグラフをかくのは意外と面倒です。
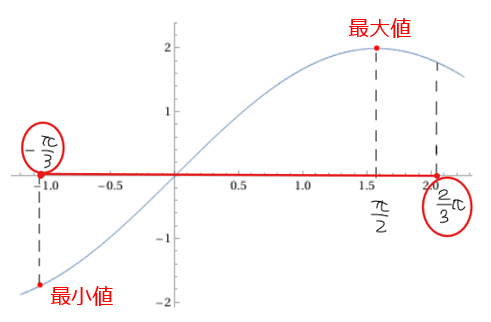
この程度の三角関数であればグラフを図示しても解けるが、縦軸・横軸方向への平行移動したグラフになってくるとグラフの図示が大変に…
そこで、三角関数ではグラフをかく代わりに、単位円を描いて最大・最小を求める方法が王道なので、その手順についてまずは本問を通して理解していきましょう。
\(\small 2\sin \theta\)の最大・最小を求める問題ですが、\(\small \theta \)によって変動するのは\(\small \sin \theta\)の部分なので、本質的には\(\small \sin\theta\)の最大・最小を求めてあげればよいことになります [*1]。
*1:【補足】\(\small \sin\theta\)の最大・最小を考えればよい理由
例えば、”\(\small 2a\)”の最大・最小を考えるとき、\(\small a\)が変数で\(\small 2\)は定数(一定の値)なので、当たり前ですが\(\small a\)の値が大きいほど\(\small 2a\)の値も大きくなりますし、逆に\(\small a\)の値が小さいほど、\(\small 2a\)の値も小さくなります。
この考え方と同様に、今回の問題では”\(\small 2\sin\theta\)”の\(\small \sin \theta\)が\(\small a\)の部分に相当すると考えれば、\(\small \sin \theta\)が最大・最小になる点が\(\small 2\sin\theta\)の最大・最小になる点であると求めることができます。
\(\small \sin\)の値の最大・最小を求める問題では、単位円を描いて指定された角度の範囲内で縦軸が最大になる点と最小になる点を確認します [*2]。
*2:【補足】単位円と\(\small \sin \)、\(\small \cos \)の値の関係
下図のように、単位円(半径が1の円のこと)では三角形の斜辺が1になるので、横軸の値が\(\small \cos\)の値、縦軸の値が\(\small \sin\)の値になります。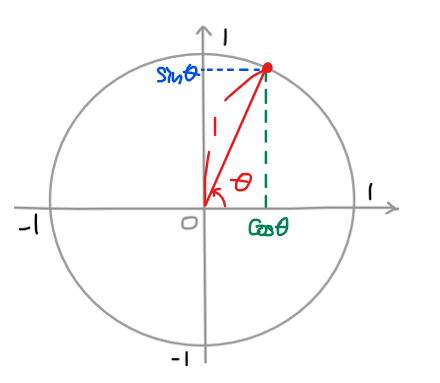
\(\small \displaystyle -\frac{\pi}{3}≦\theta ≦\frac{2}{3}\pi\)の範囲を単位円上に図示すると下図の赤線部分になります。
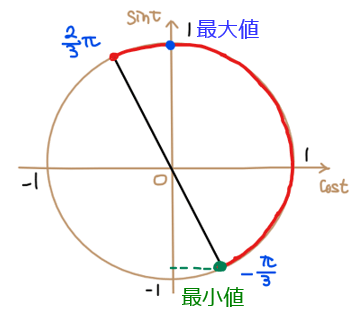
この範囲内で\(\small \sin\theta\)が最大・最小になる点を探します。すなわち、単位円上の赤色部分で縦軸の値が最大・最小になる点を探します。すると、図より、青丸箇所が最大、緑丸箇所が最小になることが分かります。
あとは、最大値、最小値とそのときの角度\(\small \theta\)の値を求めればOKでしょう。
\(\small \sin \theta \)の最大値は、\(\small \displaystyle \theta =\frac{\pi}{2}\)で、最大値 \(\small 1\)なので、\(\small 2\sin\theta\)の最大値は2倍することで、\(\small \displaystyle \theta =\frac{\pi}{2}\)で、最大値 \(\small 2\)…【答】になります [*3]。
*3:【補足】\(\small 2\sin\theta\)が最大値をとるときの角度
\(\small \sin\theta\)の最大値が1なので\(\small 2\sin\theta\)の最大値は2倍した2になりますが、最大値をとるときの単位円上の位置(角度)が青丸箇所であることは変わらないので、\(\small \displaystyle \theta = \frac{\pi}{2}\)は2倍しないことに注意しましょう。
続いて最小値ですが、こちらは微妙な位置にあり値を求めるが難しそうですね…。ですが、単位円を活用することで値を求めることができます。
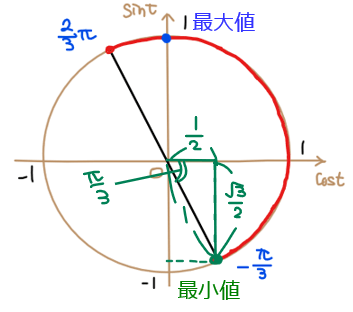
緑色の三角形に着目すると角度が\(\small \displaystyle \frac{\pi}{3}\)の三角形なので、縦軸方向の辺の長さは\(\small \displaystyle \frac{\sqrt{3}}{2}\)になるので、最小値は\(\small \displaystyle -\frac{\sqrt{3}}{2}\)になります。また、このときの角度の値は、緑丸箇所の角度なので\(\small \displaystyle \theta =-\frac{\pi}{3}\)です。
よって、\(\small \sin\theta\)の最小値は\(\small \displaystyle \theta =-\frac{\pi}{3}\)で、最小値 \(\small \displaystyle -\frac{\sqrt{3}}{2}\)なので、\(\small 2\sin\theta\)の最大値は2倍することで、\(\small \displaystyle \theta =-\frac{\pi}{3}\)で、最小値 \(\small \displaystyle -\sqrt{3}\)…【答】となります。
【問題2】範囲指定がある三角関数の最大最小【実践編】(難易度:★★★)
\(\small 0≦\theta≦\pi\)のとき、\(\small f(\theta)= 3\sin \theta +2\cos \theta\)の最大値、最小値を求めよ。 [類 福島大]
・角度が求まらない場合の最大値、最小値の求め方は、三角関数の合成を利用した最大値・最小値の求め方(角度が分からないパターンも解説)の記事をチェック!
三角関数の合成より
\begin{split}
\small f(\theta) &\small =3\sin \theta +2\cos \theta\\
&\small =\sqrt{13}\sin\left(\theta +\alpha\right) \space \cdots ①\\
\end{split}
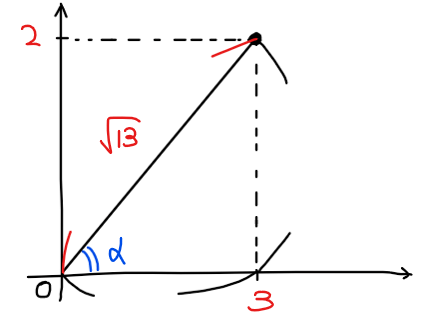
ただし、角度 \(\small \alpha\)は
\begin{split}
\begin{cases}
\small \displaystyle \sin \alpha =\frac{2}{\sqrt{13}}\\
\small \displaystyle \cos \alpha =\frac{3}{\sqrt{13}}\\
\end{cases}
\space \cdots ②
\end{split}
を満たします。
①の角度部分を \(\small t = \theta +\alpha\)と置き換えると
\begin{split}
\small f(t) &\small =\sqrt{13}\sin t\space \cdots ③\\
\end{split}
文字の置き換えをしたので、\(\small t\)の範囲についてもセットで確認しておきましょう。
\begin{split}
\small \displaystyle 0≦ &\small \theta≦\pi\\
\small \Leftrightarrow \space \color{#ef5350}{\alpha} ≦&\small \theta \color{#ef5350}{+\alpha} ≦\pi \color{#ef5350}{+\alpha}\\
\small \Leftrightarrow \space \alpha ≦&\small t ≦\pi+\alpha \cdots ④\\
\end{split}
③の最大値、最小値を求めたければ、\(\small \sin t\)の最大値、最小値を考えればよいことになります。
【補足】
\(\small \sqrt{13}\sin t\)の最大値、最小値を求める問題に帰着できたので、問題1と同じ手順で解くことができますね。
\(\small \sin t\)の最大・最小を求めるために④の範囲で単位円をかいていきます。
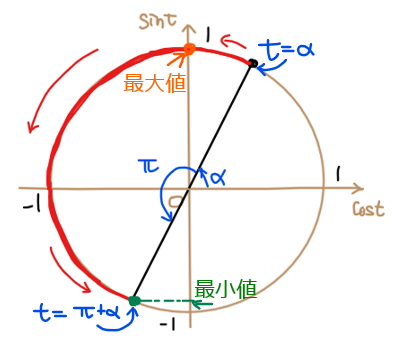
ここで、角度 \(\small t\)の範囲に\(\small \alpha \)が含まれていて、どこからどこまでの範囲なのか図示するときにつまづいてしまう人も多いかもしれません。具体的な角度が分からないときは、②で角度\(\small \alpha \)が満たす\(\small \sin, \cos\)の値は分かっているので、\(\small \sin, \cos\)の符号から第1象限~第4象限のどこにあるかくらいを把握できればOKです。
今回であれば、\(\small \sin, \cos\)が両方とも正の値なので、第1象限の角度であることが確定します [*1]。
*1:【補足】三角比の符号
単位円の横軸が\(\small \cos\)、縦軸が\(\small \sin\)であることから、三角比の符号は単位円を描けば、暗記しなくてもすぐに判断できます。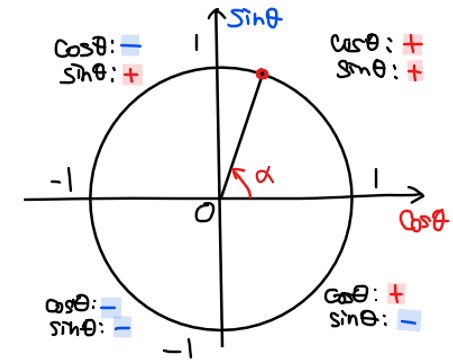
なので、冒頭の図にあるように第1象限の中の適当なところに\(\small \alpha\)をとってあげればOKです。
範囲の上限である\(\small t=\pi+\alpha\)の位置は『\(\small \alpha\)から\(\small \pi\)(180°)だけ進んだ位置』と読みかえてあげます。180°は単位円の半周分ですから、図のように\(\small t=\alpha\)の正反対の位置に\(\small t=\pi+\alpha\)をプロットしてあげればOKです。
これで、④の不等式の範囲が単位円上の赤線の範囲であることが図示できました。あとは、この赤線の範囲内で\(\small \sin t\)、すなわち単位円の縦軸が最大になる点と最小になる点を探してあげましょう。
すると、最大になるのは\(\small \displaystyle t=\frac{\pi}{2}\)のとき(オレンジ色の点)で、最小になるのは\(\small t=\pi+\alpha\)(緑色の点)になることが図から分かります。
【補足】最小値をとる点について
今回の問題で\(\small \displaystyle t= \frac{3}{2}\pi\)のときに最小値にならないのは、角度\(\small t\)の範囲外だからです。解説のところでも触れた通り、今回考えている角度の範囲は単位円の赤線範囲なので、\(\small \displaystyle t= \frac{3}{2}\pi\)は赤線範囲外になっています。最大、最小を考えるときには、関数が取り得る最大値、最小値ではなく、指定された範囲内で関数が取り得る最大値、最小値を求める必要があるという点に注意するようにしましょう。
よって、ここまでの結果をまとめると、\(\small \sin t\)は…
\(\small \displaystyle t=\frac{\pi}{2}\)のとき最大値 \(\small \displaystyle \sin \frac{\pi}{2} =1\)、
\(\small \displaystyle t=\pi+\alpha\)のとき最小値 \(\small \sin (\pi+\alpha)\)
となりますが、最小値の値が\(\small \alpha\)が入ってしまっており、\(\small \alpha\)は問題文中で与えられている文字ではないので、どうにか頑張って式変形することで、消してあげる必要があります。
\(\small \sin (\pi+\alpha)\)の形を見て式変形できることと言えば、加法定理を使って角度部分を分解することくらいしかないので、ひとまず計算してみると
\begin{split}
\small \sin (\pi+\alpha) &\small =\sin \pi \cos \alpha +\cos \pi \sin \alpha\\
&\small =0\cdot \cos \alpha +(-1)\cdot \sin \alpha\\
&\small =-\sin \alpha\\
\end{split}
となるので、②の \(\small \displaystyle \sin \alpha = \frac{2}{\sqrt{13}}\)を代入することで、
\begin{split}
\small \sin (\pi+\alpha) &\small =-\sin \alpha\\
&\small = -\frac{2}{\sqrt{13}}\\
\end{split}
と求めることができます。
よって、\(\small \sin t\)の最大値、最小値は
\(\small \displaystyle t=\frac{\pi}{2}\)のとき最大値 \(\small 1\)、
\(\small \displaystyle t=\pi+\alpha\)のとき最小値 \(\small \displaystyle -\frac{2}{\sqrt{13}}\)
なので、今回求めたい③の \(\small \sqrt{13}\sin t\)の最大値、最大値は\(\small \sqrt{13}\)倍してあげればよいので、
\(\small \displaystyle t=\frac{\pi}{2}\)のとき最大値 \(\small \sqrt{13}\)、
\(\small \displaystyle t=\pi+\alpha\)のとき最小値 \(\small \displaystyle -2\)
と求めることができます。
あとは、文字 \(\small t\)は自分で設定した文字なので、問題文にある\(\small \theta\)に戻してあげればよいでしょう。
\(\small t= \theta +\alpha\)と置き換えていたことから、最大値 \(\small \displaystyle t= \frac{\pi}{2}\)のときの\(\small \theta\)の値は
\begin{split}
\small t &\small =\theta + \alpha\\
\small \displaystyle \Leftrightarrow \space \frac{\pi}{2} &\small= \theta + \alpha \space \color{#ef5350}{◀t = \frac{\pi}{2}を代入}\\
\small \displaystyle \Leftrightarrow \space \theta &\small= \frac{\pi}{2} -\alpha\\
\end{split}
具体的な角度\(\small \alpha\)は求まらないので、\(\small \sin \theta \), \(\small \cos \theta \)の値で解答すればよいでしょう。
\begin{split}
\small \sin \theta &\small \displaystyle =\sin\left( \frac{\pi}{2} -\alpha\right)\\
&\small \displaystyle =\cos \alpha\\
&\small \displaystyle =\color{#ef5350}{\frac{3}{\sqrt{13}}} \space (∵②)\\
\end{split}
\begin{split}
\small \cos \theta &\small \displaystyle =\cos \left( \frac{\pi}{2} -\alpha\right)\\
&\small \displaystyle =\sin \alpha\\
&\small \displaystyle =\color{#ef5350}{\frac{2}{\sqrt{13}}} \space (∵②)\\
\end{split}
よって、\(\small \displaystyle \sin \theta =\frac{3}{\sqrt{13}}\), \(\small \displaystyle \cos \theta =\frac{2}{\sqrt{13}}\)のとき、最大値\(\small \sqrt{13}\)をとる…【答】と求めることができました。
同様に、最小値\(\small t= \pi +\alpha\)のときの\(\small \theta\)の値は
\begin{split}
&\small t =\theta + \alpha\\
\small \displaystyle \Leftrightarrow \space &\small \pi+\alpha = \theta + \alpha \space \color{#ef5350}{◀t = \pi + \alphaを代入}\\
\small \displaystyle \Leftrightarrow \space &\small \theta = \pi \\
\end{split}
となり、こちらは具体的な角度が求まりました。
よって、\(\small \theta = \pi\)のとき最小値\(\small -2\)をとる…【答】となります。
本記事のまとめ
本記事では、角度の範囲が指定された三角関数の最大値・最小値の求め方を、基本から入試レベルまでレベル別に解説しました。特に、三角関数の合成や文字の置き換えなど、入試頻出のテクニックをどのような流れで使うのか理解することが重要です。まずは、解法の本質が詰まった「問題1」で 単位円をかき、最大値・最小値を見つけ出すプロセス を確実にマスターしましょう。
三角関数の最大最小は、「範囲あり」になるだけで難易度が上がりますが、単位円で角度の位置を把握することができれば、安定して正答にたどりつけます。単位円の理解は三角関数全体の土台になるので、苦手な人は早めに克服しておくのがおすすめです。
また、実践的な「問題2」には、三角関数の合成・文字の置き換え・最大最小の判断といった入試レベルのポイントが詰まっています。この記事を参考に、ぜひ自分の力で解けるように演習してみてください。
他にも三角関数の最大値、最小値を求める問題についてパターン別に知りたいという人は、三角関数の最大値、最小値の求め方-三角関数の合成や二次関数への置き換えなどパターン別にわかりやすく解説!の記事で詳しく解説しているので、ぜひ確認してみてください!
今回は以上です。お疲れさまでした!





コメント