今回は、相加・相乗平均の関係を利用して最小値や最大値を求める問題について、徹底解説していきたいと思います。相加・相乗平均は公式自体は簡単なものですが、使える条件があったり、最小値、最大値を求める問題になると急に難しくて解けない…という人は多いのではないでしょうか?
この記事は、そんな悩みを解決できる記事になっていると思うので、ぜひ最後まで読んでみてください!
- 相加・相乗平均を復習したい人
- 相加・相乗平均を利用した最小値・最大値を求める問題が苦手な人
- 入試問題になると最大最小の求め方は相加・相乗平均以外にも、2次関数や微分などもあるけど、どうやったら相加・相乗平均を使う問題を見極められるのか知りたい人
- 入試レベルの相加・相乗平均を利用した問題を解きたい人
本記事の要点
今回は、相加・相乗平均の関係を利用した最大値・最小値の求め方について解説していきますが、はじめに本記事の結論をお伝えします。
☆重要Point☆
・相加・相乗平均の関係は、変数が正のときの最大値や最小値を求めるときに有効!
・最小値だけでなく、等号成立時の変数の値もしっかり確認!
・相加・相乗平均の利用にこだわりすぎずに最大値・最小値の求め方の1つと捉えておく!
では、上記の結論をもとに、問題を通して理解を深めていきましょう。
【問題&解説】相加・相乗平均を利用した最大最小
【問題1】和の最小値①(難易度:★)
\(\small x>0\)として、\(\small \displaystyle x+\frac{4}{x}\)の最小値を求めよ。
\(\small x>0\)であることから、相加・相乗平均の関係より、
\begin{split}
x+\frac{4}{x}&=2\sqrt{x\cdot \frac{4}{x}}\\
&=2\sqrt{4}\\
&=\color{red}{4\quad \cdots【答】}\\
\end{split}
最小値をとるときの\(\small x\)の値は、
\begin{split}
x&=\frac{4}{x}\quad \color{#ff7043}{◀\small 最小値は等号成立時}\\
⇔\space & x^2=4\\
⇔\space & x=2 \quad (∵ \space x>0)\\
\end{split}
●OnePoint
相加・相乗平均は変数が正のときしか使えないので、今回であれば\(\small x>0\)であることを論証することがポイントになります【詳細は講義3の「相加・相乗平均の関係」をチェック】。
●解答
最小値 4(\(\small x=2\)のとき)
【問題2】和の最小値②(難易度:★★)
\(\small x>0\)として、\(\small \displaystyle x+\frac{25}{x+3}\)の最小値を求めよ。
●問題解決のKey
2変数を\(\small x\)と\(\small \displaystyle \frac{25}{x+3}\)とみなして相加・相乗平均の関係を使おうとすると、
$$\small x+\frac{25}{x+3}=2\sqrt{x \cdot \frac{25}{x+3}}$$
となり、計算に行き詰ってしまうので、分母分子がうまく消えるような形に式変形するのがポイント
\begin{split}
x+\frac{25}{x+3}&=x\color{#ff7043}{+3}+\frac{25}{x+3}\color{#ff7043}{-3} \quad \color{#ff7043}{◀ \small 分母と同じ x+3 を作りに行く}\\
\end{split}
\(\small x+3>0\)、\(\small \displaystyle \frac{25}{x+3}>0\)から、相加・相乗平均の関係より
\begin{split}
\color{#ff7043}{(x+3)+\frac{25}{x+3}}-3&≧\color{#ff7043}{2\sqrt{(x+3)\cdot\frac{25}{x+3}}}-3\\
&=2\cdot 5 -3\\
&=\color{red}{7\quad \cdots 【答】}\\
\end{split}
念のため、\(\small x>0\)の範囲で最小値をとるかどうかも確かめておく。
最小値をとるときは等号成立のときなので、
\begin{split}
x+3&=\frac{25}{x+3}\quad \small \color{#ff7043}{◀2変数はx+3、\frac{25}{x+3}に注意}\\
(x+3)^3&=25\\
x+3&=5\quad \small \color{#ff7043}{◀x+3>0 なので}\\
x&=2\\
\end{split}
より、\(\small x=2\)のときなので、題意である\(\small x>0\)に解を持つ。
●解答
最小値 7 (\(\small x=2\)のとき)
【問題3】積の最小値(難易度:★★★)
\(\small x>0\)として、\(\small \displaystyle \left(x+\frac{1}{x}\right)\left(x+\frac{16}{x}\right)\)の最小値を求めよ。
\begin{split}
&\left(x+\frac{1}{x}\right)\left(x+\frac{16}{x}\right)\\
&=\color{#ff7043}{x^2+\frac{16}{x^2}}+17\quad \cdots①
\end{split}
\(\small \displaystyle \color{#ff7043}{x^2>0、\frac{16}{x^2}>0}\)より、相加・相乗平均の関係から
\begin{split}
\color{#ff7043}{x^2+\frac{16}{x^2}}≧2\sqrt{x^2\cdot\frac{16}{x^2}}=\color{#ff7043}8\\
\end{split}
式①に代入することで
\begin{split}
\color{#ff7043}{x^2+\frac{16}{x^2}}+17&≧\color{#ff7043}8+17\\
&=\color{red}{25 \space \cdots【答】}
\end{split}
最小値をとるときの\(\small x\)の値は、
\begin{split}
x^2&=\frac{16}{x^2}\quad \color{#ff7043}{◀\small 最小値は等号成立時}\\
⇔\space & x^4=16\\
⇔\space & x=\sqrt{2} \quad (∵ \space x>0)\\
\end{split}
●よくある失敗
積のそれぞれに対して、相加・相乗平均の関係を利用することで
\begin{split}
x+\frac{1}{x}&≧2\sqrt{x\cdot\frac{1}{x}}=2\\
x+\frac{16}{x}&≧2\sqrt{x\cdot\frac{16}{x}}=8\\
\end{split}
より、
\begin{split}
\left(x+\frac{1}{x}\right)\left(x+\frac{16}{x}\right)&≧
2\cdot 8=16\\
\end{split}
とするのは間違い…
\(\small \displaystyle x+\frac{1}{x}\)が最小値2となるのは \(\small x=1\)のときだが、\(\small \displaystyle x+\frac{16}{x}\)が最小値8となるのは \(\small x=4\)のときであり、両方同時に最小にはならないことに注意する。
●解答
最小値 25(\(\small x=\sqrt{2}\)のとき)
【問題4】変数の範囲に制限がある場合の最小値(難易度:★★★)
\(\small 2≦x≦5\)のとき、\(\small \displaystyle x+\frac{3}{x}\)の最小値を求めよ。
\(\small x>0\)より、相加・相乗平均の関係を用いると
\begin{split}
x+\frac{3}{x}&≧2\sqrt{x\cdot\frac{3}{x}}\\
&=2\sqrt{3}\\
\end{split}
等号成立時(最小値をとるときの)の\(\small x\)の値は、
\begin{split}
x&=\frac{3}{x}\\
x^2&=3\\
∴\space x&=\pm \sqrt{3}\\
\end{split}
となるが、これは\(\small 2≦x≦5\)の範囲外のため不適。
\(\small 2≦x≦5\)の範囲では、\(\small \displaystyle x+\frac{3}{x}\)は単調増加(\(\small x\)が大きいほど値が大きくなる)であることから、\(\small x=2\)のときが最小値となり、その値は
$$\left. x+\frac{3}{x}\right|_{x=2}=2+\frac{3}{2}=\color{red}{\frac{7}{2}\space \cdots【答】}$$
●解答
最小値 \(\small \displaystyle \frac{7}{2}\) (\(\small \space x=2\)のとき)
●OnePoint:等号成立を確認する理由
本問のように、変数\(\small x\)に条件が課されているときは、そもそも最小値をとる変数の値が条件を満たさない場合があるため、最小値をとるときの変数の値までしっかり確認するようにしたい【詳細は講義4の「注意点其の2」をチェック】。
【問題5】最大値を求める問題(難易度:★★)
\(\small x\)が正の数のとき、\(\small \displaystyle \frac{2x}{x^2+5}\)の最大値を求めよ。
●問題解決のKey
分母が最小=式全体は最大
\(\small x>0\)より、分母分子を\(\small x\)で割ると
\begin{split}
\small \frac{2x}{x^2+5}& \small =\frac{2}{x+\dfrac{5}{x}}\quad \cdots①\\
\end{split}
分母に対して相加・相乗平均の関係を用いると
\begin{split}
\small x+\dfrac{5}{x}≧2\sqrt{x\cdot\frac{5}{x}}=2\sqrt{5}\\
\end{split}
(等号成立は\(\small x=\sqrt{5}\)のとき)。
式①で分母が最小となるとき、式全体としては最大となるため、
\begin{split}
\small \frac{2}{\color{#ff7043}{x+\dfrac{5}{x}}}≦\frac{2}{\color{#ff7043}{2\sqrt{5}}}=\color{red}{\frac{1}{\sqrt{5}}\quad \cdots【答】}\\
\end{split}
●OnePoint
「分母が最小のとき、式全体は最大となる」という論証は、相加・相乗平均で導いた関係式を用いて、
\begin{split}
\small x+\dfrac{5}{x}& \small ≧2\sqrt{5}\\
\small \dfrac{1}{x+\dfrac{5}{x}}& \color{magenta}≦\small \frac{1}{2\sqrt{5}}\quad \color{magenta}{◀逆数をとると大小関係が逆転}\\
\small \dfrac{2}{x+\dfrac{5}{x}}& ≦\small \frac{1}{\sqrt{5}}\quad \color{magenta}{◀両辺を2倍}\\
\end{split}
と数式的に示してもよい。
●解答
最大値 \(\small \displaystyle \frac{1}{5}\)(\(\small x=\sqrt{5}\)のとき)
【問題6】部分分数分解を利用した最小値問題(難易度:★★★★)
\(\small x>0\)のとき、\(\small \displaystyle \frac{x^2+2}{\sqrt{3x^2+1}}\)の最小値を求めよ。
●問題解決のKey
分母分子にルートの中身と同じ形を作って、
$$\small \frac{\color{#ff7043}●+■}{\sqrt{\color{#ff7043}●}}=\frac{\color{#ff7043}●}{\sqrt{\color{#ff7043}●}}+\frac{■}{\sqrt{\color{#ff7043}●}}=\sqrt{\color{#ff7043}●}+\frac{■}{\sqrt{\color{#ff7043}●}}$$
のような形に部分分解することで、相加・相乗平均の関係が利用できる。
\(\small x>0\)より、相加・相乗平均の関係を用いることで
\begin{split}
\small \frac{\color{#ff7043}{x^2+2}}{\sqrt{3x^2+1}}&=\small \frac{\color{#ff7043}{\dfrac{1}{3}(3x^2+6)}}{\sqrt{3x^2+1}} \quad \color{#ff7043}{◀分母の3x^2に近づけていく}\\
&=\small \frac{\color{#ff7043}{\dfrac{1}{3}\left[(3x^2+1)+5\right]}}{\sqrt{3x^2+1}}\\
&\small =\frac{1}{3}\left( \frac{3x^2+1}{\sqrt{3x^2+1}}+\frac{5}{\sqrt{3x^2+1}}\right)\\
&\small =\frac{1}{3}\left(\color{#ff7043}{\sqrt{3x^2+1}}+\frac{5}{\sqrt{3x^2+1}}\right)\quad \color{#ff7043}{◀\frac{●}{\sqrt{●}}=\sqrt{●}で変形}\\
&\small ≧\frac{1}{3}\left( 2\cdot \sqrt{\sqrt{3x^2+1}\cdot \frac{5}{\sqrt{3x^2+1}}}\right)\\
&\small = \frac{2\sqrt{5}}{3}\\
\end{split}
等号成立時の\(\small x\)の値は、
\begin{split}
\small \sqrt{3x^2+1}& \small =\frac{5}{\sqrt{3x^2+1}}\\
\small 3x^2+1& \small =5\\
\small 3x^2& \small =4\\
\small x& \small =\frac{2}{\sqrt{3}}\quad(∵\space x>0)\\
\end{split}
よって、最小値は\(\small \displaystyle \color{red}{\frac{2\sqrt{5}}{3}}\) …【答】.
●解答
最小値 \(\small \displaystyle \color{red}{\frac{2\sqrt{5}}{3}} \left( x=\frac{2}{\sqrt{3}} のとき\right)\)
【問題7】条件確認が必要な最小問題(難易度:★★★)
\(\small \displaystyle x^2+x+\frac{1}{x^2+x+1}\)の最小値を求めよ。
●問題解決のKey
問題自体は\(\small x^2+x+1\)の形を分母分子に作り出すことで相加・相乗平均の関係が利用できそうだとわかれば、解法自体は難しくないが、今回のポイントは論証。
相加・相乗平均を使用するためには、変数が\(\small x^2+x+1>0\)の条件を満たす必要がある【講義4の注意点其の1】ので、この論証がないと減点対象に…。
\(\small \displaystyle x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\)(※)より、相加・相乗平均の関係を用いることで
\begin{split}
x^2+x+\frac{1}{x^2+x+1}&=\color{#ff6900}{(x^2+x+1)+\frac{1}{x^2+x+1}}-1\\
&≧\color{#ff6900}{2\sqrt{(x^2+x+1)\cdot \frac{1}{x^2+x+1}}}-1=1\\
\end{split}
※補足:\(\small \displaystyle \left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\)>0になる理由
一般に実数の2乗はゼロ以上(\(\small ●^2≧0\))になるので、ゼロ以上の数に\(\small \displaystyle \frac{3}{4}\)を足した数は0より大きな実数になるため、上記の不等号が成り立つ。
等号成立は、
\begin{split}
&x^2+x+1=\frac{1}{x^2+x+1}\\
\Leftrightarrow \space & (x^2+x+1)^2=1\\
\Leftrightarrow \space & x^2+x+1=1\quad(∵\space x^2+x+1>0)\\
\Leftrightarrow \space & x(x+1)=0\\
∴ \space & x=-1、0\\
\end{split}
よって、\(\small x=-1、0\)のとき、最小値\(\small 1\)…【答】.
●OnePoint
等号成立時の\(\small x\)の値が、\(\small x=-1、0\)と出てきたので、\(\small x>0\)ではないから不適では?と思うかもしれませんが、変数>0の条件は、あくまで相加・相乗平均の関係を使うときの変数が正でなくてはいけないという条件であり、本問であれば\(\small x^2+x+1\)が正であれば\(\small x\)自体が正でなくてもよい点に注意されたい。
●解答
最小値 1(\(\small x=-1、0\)のとき)
【問題8】変数が負の場合の相加・相乗平均の利用(難易度:★★★)
\(\small \displaystyle \frac{x}{x^2+2x+2}\)の最小値を求めよ。
●問題解決のKey
\(\small x \neq 0\)として、\(\small \displaystyle \frac{x}{x^2+2x+2}=\frac{1}{\color{#ff6900}{x+\dfrac{2}{x}}+2}\)と変形した場合、分母に相加・相乗平均の形が現れるが、\(\small x>0\)の条件がない。
さらに問題の式をもう一歩踏み込んで考察すると、\(\small x^2+2x+2=(x+1)^2+1>0\)より、式の分母は常に正だが、分子は\(\small x\)の値によって正にも負にもなり得るため、最小値をとるときの\(\small x\)の値は\(\small x<0\)になることが分かる。
一見すると相加・相乗平均の関係を利用できなさそうだが、うまく文字を置き換えることで【変数>0】の形を作り出せるかがポイント。
問題の式の分母について、\(\small x^2+2x+2=(x+1)^2+1>0\)であることから、問題の式が最小値をとるとき、変数\(\small x\)は必ず\(\small x<0\)となる。

符号の大小関係的に式の値が負となる\(\small x<0\)の範囲で最小値をとることが分かる
よって、\(\small x<0\)の範囲で考えても一般性を失わない。
\(\small x=-t\)とおくと、\(\small \displaystyle t>0、\frac{1}{t}>0\)より、
\begin{split}
\frac{x}{x^2+2x+2}&=\frac{-t}{t^2-2t+2}\\
&= -\frac{1}{t-2+\dfrac{2}{t}}\\
&= -\frac{1}{t+\dfrac{2}{t}-2} \quad \cdots①\\
\end{split}
①の分母に対して、相加・相乗平均の関係を用いることで、
\begin{split}
\color{#ff6900}{t+\dfrac{2}{t}}-2&≧2\sqrt{\color{#ff6900}{t \cdot \frac{2}{t}}}-2\\
&=2\sqrt{2}-2\\
\end{split}
等号成立は、
\begin{split}
t&=\frac{2}{t}\\
\Leftrightarrow \space t^2&=2\\
∴ \space t&=\sqrt{2}\space(t>0)\\
\end{split}
より、\(\small x=-t\)とおいていたことから、\(\small x=-\sqrt{2}\)のときに最小値をとる。
最後に、最小値は、式①の分母が最小となるとき式全体も最小となることから、
\begin{split}
-\frac{1}{t+\dfrac{2}{t}-2}&≧-\frac{1}{2\sqrt{2}-2}\\
&=\color{red}{-\frac{\sqrt{2}+1}{2}\cdots【答】}
\end{split}
●OnePoint
本問は式全体が負なので、大小評価では分母が最小となるときに、式全体としても最小となることに注意されたい(式全体が正であれば、分母が最小のとき式全体は最大となる)。
具体例で考えれると、\(\small \displaystyle -\frac{1}{100}>-\frac{1}{10}>-\frac{1}{2}\)のように分母が小さくなるにつれて全体の値自体も小さくなっていく(より負の方向にいく)ことが分かる。
●解答
最小値 \(\small \displaystyle -\frac{\sqrt{2}+1}{2}\)(\(\small x=-\sqrt{2}\)のとき)
【入試問題に挑戦】相加相乗平均を利用した最小値
\(\small x>1\)のとき、\(\small \displaystyle 4x^2+\frac{1}{(x+1)(x-1)}\)の最小値とそのときの\(\small x\)の値を求めよ。 [類 慶応義塾大]
●問題解決のKey
問題文中の\(\small x>1\)から\(\small x^2-1>0\)となることと、求める式の形が「●+\(\small \frac{■}{●}\)」に変形できる形になっており、\(\small x^2-1\)の形も含まれていることから、相加相乗平均の関係を使って解けるのではないかという読みができるとよい。
\begin{split}
&\small 4x^2+\frac{1}{(x+1)(x-1)}\\
&\small =4(x^2\color{#ff7043}{-1})+\frac{1}{x^2-1}\color{#ff7043}{+4} \quad \color{#ff7043}{◀分母のx^2-1と同じ形を作りにいく}\\
\end{split}
\(\small x>1\space \Leftrightarrow x^2>1 \space \Leftrightarrow \color{#ff7043}{x^2-1>0}\)より、相加・相乗平均の関係から
\begin{split}
&\small 4(x^2-1)+\frac{1}{x^2-1}+4\\
& \small ≧2\sqrt{4(x^2-1)\cdot\frac{1}{x^2-1}}+4\\
&\small =4+4=8\\
\end{split}
等号成立時の\(\small x\)の値は
\begin{split}
\small 4(x^2-1)& \small =\frac{1}{x^2-1}\\
\small (x^2-1)^2& \small =\frac{1}{4}\\
\small x^2-1& \small =\frac{1}{2}\quad(∵\space x^2-1>0)\\
\small x^2& \small =\frac{3}{2}\\
\small x& \small =\frac{\sqrt{6}}{2}\quad(∵\space x>1)\\
\end{split}
よって、\(\small \displaystyle x=\frac{\sqrt{6}}{2}\)のとき、最小値8…【答】.
【徹底解説】相加・相乗平均を利用した最小・最大問題
相加・相乗平均の関係とは、相加平均と相乗平均の間に成り立つ関係式のことです。なので、関係性の話をする前に、まずは、相加平均と相乗平均がそれぞれどういう意味なのかについて簡単に復習しておきましょう。
【講義1】相加平均とは?
●相加平均とは
$$(\mathsf{相加平均})=\frac{a+b}{2}$$
いわゆる”平均”のことです。なので、相加平均と聞くと難しそうに感じますが、テストの平均点とか男女別の平均身長など日常生活のあらゆる場面で利用されているなじみ深い概念ですね。
【講義2】相乗平均とは?
●相乗平均とは
$$(\mathsf{相乗平均})=\sqrt{ab}$$
こちらは聞きなじみがない平均ですね。相加平均を【足し算の平均】というならば、相乗平均とは、”かけ算の平均”ということができます。ちょっとイメージしにくいと思うので、簡単な例で考えてみましょう。
●例題
ある都市の人口が2倍、8倍と年々増加した場合、人口は1年間で平均何倍増加したでしょうか?
●よくある失敗例
2倍と8倍の平均だから、\(\small \displaystyle \frac{2+8}{2}=5\)倍…というのは間違い。
もし仮に年間5倍増加していたとすると、2年間では\(\small 5 \times 5 =25\)倍増加したことになるが、実際は、\(\small 2 \times 8 =16\)倍。
●分かりやすい解説
2年間全体では、\(\small 2×8=16\)倍になったということは、毎年平均\(\small x\)倍に増加だったとすると、2年間では\(\small x^2\)倍となり、これが16倍になればよいので
\begin{split}
\small x^2&=16\\
\small x&=4\quad (∵\space x>0)\\
\end{split}
よって、平均4倍増加したことになります。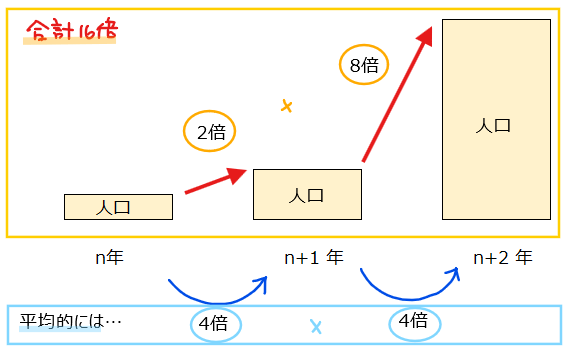
例題で求めた平均4倍という増加率は、実は相乗平均を用いると、
$$\small \mathbf{相乗平均} = \sqrt{2\times8}=4$$
とあっという間に計算できます。
このように相乗平均は、変化率のようなかけ算の平均を求める場合に利用されています。
【講義3】相加平均と相乗平均の関係
相加平均と相乗平均についてなんとなくわかったところで、ここからが本題です!
相加平均と相乗平均の間には次のような関係性があります。
●相加平均と相乗平均の関係性
相加平均 ≧ 相乗平均
相加平均\(\small \displaystyle \left( \frac{a+b}{2} \right)\)は、相乗平均(\(\small \sqrt{ab}\))以上になるという関係が成り立ちます。先程の人口増加の例題でも、相加平均(5倍)≧相乗平均(4倍)となっていましたね。
数式で表すと
$$\frac{a+b}{2}≧\sqrt{ab}$$
ですが、数学の問題では両辺を2倍して分数をなくした形で出てくることが多いので、次の関係で覚えておくのがおすすめです。
【超重要】相加・相乗平均の関係
\(\small a>0、b>0\)のとき、
$$\small \color{red}{ a+b≧2\sqrt{ab}}$$
が成り立つ(等号成立は、\(\small a=b\) のとき)。
【講義4】相加・相乗平均を利用するときの注意点
相加・相乗平均の関係式が不等式になっていることから、テストや大学入試では相加・相乗平均の関係の関係式を利用した式の最小値を求める問題がよく出題されます。
ただ、本来、相加・相乗平均の関係は最小値を求めるための公式ではないので、使いどころには注意が必要です。
【注意点其の1】相加・相乗平均の関係が使える条件
相加・相乗平均の関係は、変数が正のときしか使えません。
なので、解答するときは変数が正であることを必ず確認しましょう。
変数が正でなくてはならない理由は、相乗平均の定義が\(\small \sqrt{ab}\)のように平方根を含むため、中身の変数は正でないといけないと覚えておくのがよいでしょう。
【注意点其の2】等号成立時の変数(\(\small x\))の値は要確認
相加・相乗平均の関係式を利用して【(式の値)\(\small ≧■\)】のような関係が導けたとしても、必ずしも【■=最小値】とは限りません。
そのため、最小値をとるときの変数の値が存在するかについてしっかり確認しておくことが大切です。
注意点其の2について、「相加・相乗平均の関係から求めた値が最小値になるとは限らないってどういうこと!?」と混乱した人もいると思うので、簡単な問題で説明しましょう。
hiroemon大学の入学試験は合格ボーダーが70点だったとします。このとき、今年の合格者の中で最低点だった人の点数は何点でしょうか?
もちろん、明確な答えは分かりません(いきなり問題出しておいてあれですが…)。ただし合格しているということは、少なくても70点以上の点数であることは確かなので、合格者の最低得点を\(\small x\)とするならば、\(\small x≧70\)という不等式は成り立ちます。
ただし、\(\small x≧70\)の関係式が成り立つからと言って、必ずしも\(\small x=70\)、すなわち合格者の最低得点が70点になるかどうかは別問題で、実際には最低得点は80点だったかもしれませんし、本当に70点ぎりぎりの合格者がいたかもしれません。
つまり、注意点其の2で言いたかったことは、「不等式が成り立つからと言って、必ず等号が成立するとは限らない」ということです。なので、相加・相乗平均の関係を利用した最小値問題では、必ず等号成立を確認するようにしましょう。
【講義5】相加・相乗平均の使いどころ
相加・相乗平均を利用した最大、最小問題を勉強すると、多くの人は「どんなときに相加・相乗平均を使って最大最小を求めればいいの?」という疑問が湧いてくると思います
これは数学をどこまで勉強しているかによって答えが異なります。
数Ⅲまで学習している理系志望の人であれば、数Ⅲで微分を習うので、正直最大最小問題は微分で解けばOKです。強いて言うなら、相加・相乗平均を使った方が計算が圧倒的に楽になるので、気づいたらラッキーと思って使えばいいくらいの感覚でいいと思います。
一方で、数学Ⅱまでが出題範囲のテストだったり、文系志望の人であれば、問題文中に「変数が正(変数>0)」という条件がある最大・最小問題であれば、相加・相乗平均が使える可能性が高いです(数Ⅱの微分や2次関数などで解けそうな最大最小問題は、もちろんそのまま解けばOK)。
他には、求める式の形が「●+\(\small \frac{■}{●}\)」の形になっている(または変形できる)ことが多いので、問題慣れをしておけば、式の見た目からも気づけるようになると思います。
本記事のまとめ
今回は、相加・相乗平均の関係式を利用した最大値、最小値の求め方について実践的な問題を解説してきましたがいかがでしたか?
最後に、本記事の重要Pointを簡単に振り返っておきましょう。
☆重要Point☆
・相加・相乗平均の関係は、変数が正のときの最大値や最小値を求めるときに有効!
・最小値だけでなく、等号成立時の変数の値もしっかり確認!
・相加・相乗平均の利用にこだわりすぎずに最大値・最小値の求め方の1つと捉えておく!
今回は以上です。お疲れ様でした!








コメント