正弦定理・余弦定理を応用した平面図形・空間図形の問題【基礎～入試対策までパターン別に徹底解説】

今回は、正弦定理・余弦定理を応用した平面図形・空間図形の問題について解説していきます。

「正弦定理と余弦定理のどちらを使えばいいのか分からない…」、「空間図形の把握が苦手…」といった悩みを持っている人向けに、公式利用の見極め方や使いどころ、問題を解くアプローチまで徹底解説していきます。ぜひ最後までチェックしてみてください！

　本記事はこんな人におすすめ

正弦定理と余弦定理のどちらを使えばよいかがわからない人
平面図形で辺や角度、面積など求める問題がが苦手な人
空間図形の問題が苦手な人
平面図形や空間図形で頻出の公式＆定理を知りたい人
入試問題にチャレンジして実力を確かめたい人

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

本記事の要点
【問題＆解説】平面図形問題
【問題＆解説】空間図形問題
1. 【問題5】正四面体の切り口の面積（難易度：★★）
2. 【問題6】正四面体の体積・垂線（難易度：★★★）
【徹底解説】正弦定理と余弦定理の応用問題へのアプローチ
本記事のまとめ

本記事の要点

今回は、正弦定理・余弦定理を応用した平面図形・空間図形問題の解き方について解説していきますが、はじめに本記事の結論をお伝えします。

☆重要Point☆
・問題文は必ず図で描いて視覚的に捉える。
・空間図形は平面図形に切り出して考える。
・正弦定理・余弦定理も重要だが、図形的な性質の利用も忘れない。

では、上記の結論をもとに、問題を通して理解を深めていきましょう。

【問題＆解説】平面図形問題

【問題1】辺の長さを求める問題①（難易度：★）

問題1：辺の長さを求める問題①

$\small \displaystyle \sin \mathrm{A}=\frac{3}{\sqrt{11}}$、$\small \mathrm{AB}=2\sqrt{11}$、$\small \mathrm{BC}=7$である鋭角三角形$\small \mathrm{△ABC}$がある。このとき、$\small \mathrm{AC}$の値を求めよ。 [東北学院大]

問題解決のKey

問題文の条件を図式化すると下図のようになる。

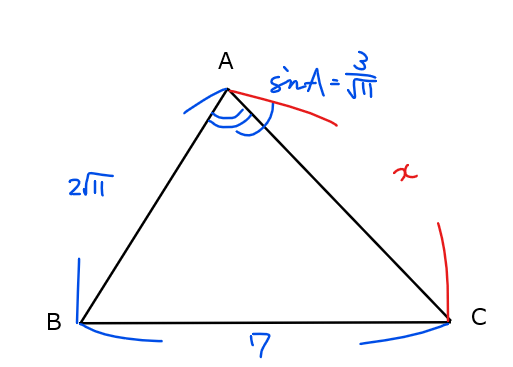
この図からもわかる通り、向か合う辺と角が2組揃っていないので、余弦定理を使って解いていくのが定石。余弦定理を使うために問題文の$\small \sin \mathrm{A}$を、鋭角三角形であるという条件に注意して$\small \cos \mathrm{A}$に変換してあげればよい。

　解説

$\small \mathrm{△ABC}$が鋭角三角形のとき、$\small \cos \mathrm{A}>0$であることに注意して、三角比の関係から

\begin{split}
\small \sin^2 \mathrm{A}& \small +\cos^2 \mathrm{A}=1\\
\small \cos^2 \mathrm{A}&\small =1-\left(\frac{3}{\sqrt{11}}\right)^2\\
\small \cos^2 \mathrm{A}&\small =\frac{2}{11}\\
\small \cos \mathrm{A}&\small =\sqrt{\frac{2}{11}}\quad(∵\space \cos \mathrm{A}>0)\\
\end{split}

●OnePoint：三角比の符号
・$\small \angle \mathrm{A}$が鋭角のとき
　$\small \sin \mathrm{A}>0$、$\small \color{red}{\cos \mathrm{A}>0}$
・$\small \angle \mathrm{A}$が鈍角のとき
　$\small \sin \mathrm{A}>0$、$\small \color{blue}{\cos \mathrm{A}<0}$

$\small \mathrm{AC}=x$とおき、$\small \mathrm{△ABC}$において、余弦定理を用いることで、

\begin{split}
\small \mathrm{BC}^2 & \small =\mathrm{AB}^2+\mathrm{AC}^2-2\mathrm{AB}\cdot \mathrm{AC} \cdot \cos\mathrm{A}\\
\small 49 & \small =44 + x^2 -2\cdot 2\sqrt{11} \cdot x \cdot \sqrt{\frac{2}{11}}\\
\small \Leftrightarrow \space x^2 &\small -4\sqrt{2}x-5=0\\
\small ∴\space x & \small =2\sqrt{2}\pm \sqrt{13}\\
\end{split}

$\small x$は辺$\small \mathrm{AC}$の長さなので、$\small x>0$であることから、$\small \mathrm{AC}=2\sqrt{2}+\sqrt{13}$…【答】.

●OnePoint
問題文で与えられている情報が$\small \sin \mathrm{A}$なので、正弦定理を使う問題に見えますが、わかっている辺や角の情報から余弦定理を使うと見極めが必要になります。
余弦定理では$\small \cos \mathrm{A}$になるので、間違って$\small \sin \mathrm{A}$のまま計算しないように注意しましょう。

【問題2】辺の長さを求める問題②（難易度：★★★）

問題2：辺の長さを求める問題②

$\small △\mathrm{ABC}$において、$\small \mathrm{AB}=8$、$\small \mathrm{AC}=4$、$\small \angle{\mathrm{A}}=120°$とする。$\small \angle{\mathrm{A}}$の二等分線と辺$\small \mathrm{BC}$の交点を$\small \mathrm{D}$とするとき、線分$\small \mathrm{AD}$の長さを求めよ。

問題解決のKey

問題文の条件を図で整理すると下図のようになるので

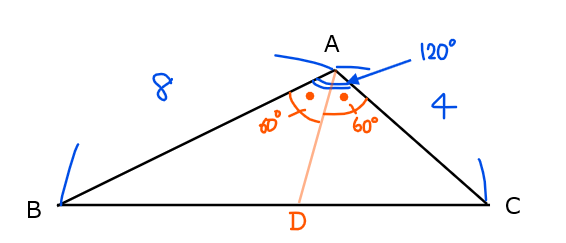
求める辺$\small \mathrm{AD}$を含む三角形について正弦定理、余弦定理が使えないかを考えるのが定石だが、そのまま余弦定理を適用してもうまくいかない。この問題では、見方によって、$\small \mathrm{△ABC}$、$\small \mathrm{△ABD}$、$\small \mathrm{△ADC}$の3つの三角形があるので、それぞれについて、正弦定理・余弦定理の使い分け方【詳細は講義1を参照】に則って立式してけるかがポイント。

　解説

$\small \mathrm{△ABC}$において、余弦定理から

\begin{split}
\small \mathrm{BC}^2& \small =8^2+4^2-2\cdot 8 \cdot 4 \cdot \cos 120°\\
& \small =64+16-64 \cdot \left(-\frac{1}{2}\right)\\
& \small =112\\
\small ∴\space \mathrm{BC} & \small = 4\sqrt{7}\\
\end{split}

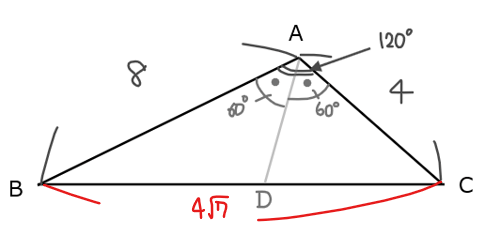
$\small \mathrm{△ABC}$において、角の二等分線の性質から、$\small \color{#ff6900}{\mathrm{BD}:\mathrm{DC}}=\mathrm{AB}:\mathrm{AC}=\color{#ff6900}{2:1}$より、

\begin{split}
\small \mathrm{BD} & \small =\frac{2}{3}\mathrm{BC}=\frac{8\sqrt{7}}{3}\\
\small \mathrm{DC} & \small =\frac{1}{3}\mathrm{BC}=\frac{4\sqrt{7}}{3}\\
\end{split}

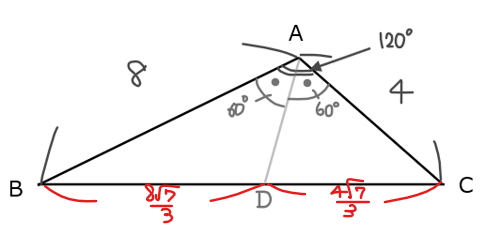
次に、求める辺を$\small \mathrm{AD}=x$とおく。

$\small \mathrm{△ABD}$において、余弦定理を用いることで

\begin{split}
\small \mathrm{BD}^2 & \small =\mathrm{AB}^2+\mathrm{AD}^2-2\mathrm{AB}\cdot \mathrm{AD} \cdot \cos60°\\
\small \left( \frac{8\sqrt{7}}{3}\right)^2 & \small =8^2+x^2-2\cdot 8x\cdot \left(\frac{1}{2}\right)\\
\small x^2-8x & \small +\frac{128}{9}=0 \quad \cdots ①\\
\end{split}

同様に、$\small \mathrm{△ADC}$でも余弦定理より

\begin{split}
\small \mathrm{DC}^2 & \small =\mathrm{AD}^2+\mathrm{AC}^2-2\mathrm{AD}\cdot \mathrm{AC} \cdot \cos60°\\
\small \left( \frac{4\sqrt{7}}{3}\right)^2 & \small =4^2+x^2-2\cdot 4x\cdot \left(\frac{1}{2}\right)\\
\small x^2-4x & \small +\frac{32}{9}=0 \quad \cdots ②\\
\end{split}

②-①より

\begin{split}
\small 4x & \small = \frac{96}{9}\\
\small ∴ \space x & \small = \frac{8}{3}\\
\end{split}

よって、線分$\small \displaystyle \mathrm{AD}=\frac{8}{3}$…【答】.

　別解

「2辺とその間の角」が分かっているので、三角形の面積の関係を利用することで、簡単に求めることができる。

\begin{split}
\small \mathrm{△ABC}& \small =\mathrm{△ABD}+\mathrm{△ADC}\\
\small \frac{1}{2}\cdot 8 \cdot 4 \cdot \sin120° & \small =\frac{1}{2}\cdot 8 \cdot \mathrm{AD} \sin 60°+\frac{1}{2}\cdot 4 \cdot \mathrm{AD} \sin 60°\\
\small 8 & \small = 3\mathrm{AD} \quad \color{#ff7043}{◀\sin120°=\sin60°=\frac{\sqrt{3}}{2}なので約分可}\\
\small ∴ \space \mathrm{AD} & \small = \frac{8}{3}\\
\end{split}

【問題3】円に内接する四角形の面積（難易度：★★）

問題3：円に内接する四角形の面積

円に内接する四角形$\small \mathrm{ABCD}$を考える。$\small \mathrm{AB}=\mathrm{AD}=\sqrt{7}$、$\small \mathrm{BC}=1$、$\small \mathrm{CD}=5$のとき、四角形$\small \mathrm{ABCD}$の面積を求めよ。

問題解決のKey

円に内接する四角形では向かい合う角度の合計が$\small 180°$になることを利用する。円に内接する四角形の問題は、四角形を2つの三角形に切り分けて考えるのが定石。2つの三角形が出てきたときには、それぞれの三角形に対して余弦定理を適用し、2本の式を立式してあげるとうまくいくことが多い。

　解説

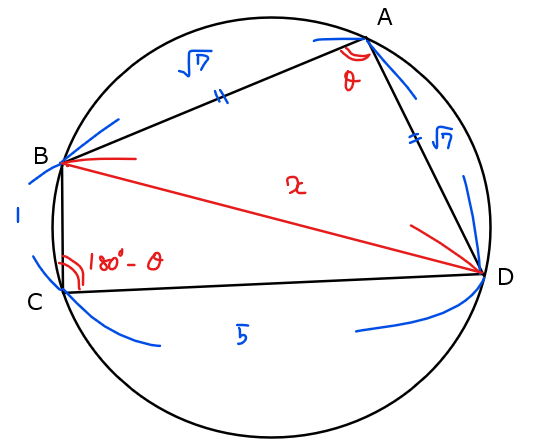
$\small \mathrm{BD}=x$、$\small \angle \mathrm{BAD}=\theta$とおく。

$\small \mathrm{△ABD}$において、余弦定理より

\begin{split}
\small x^2 & \small =(\sqrt{7})^2+(\sqrt{7})^2-2\cdot \sqrt{7} \cdot \sqrt{7} \cdot \cos \theta\\
\small x^2 & \small =14-14\cos \theta\quad\cdots①\\
\end{split}

円に内接する四角形の性質【頻出公式No.7】より、$\small \color{red}{\angle \mathrm{BCD}=180°-\theta}$であることから、$\small \mathrm{△BCD}$において、余弦定理より

\begin{split}
\small x^2 & \small =(1)^2+(5)^2-2\cdot 1 \cdot 5 \cdot \cos(180°-\theta)\\
\small x^2 & \small =26-10\cdot \color{#ff6900}{ (-\cos \theta)}\quad \color{#ff6900}{◀ \cos(180°-\theta)=-\cos \thetaを利用}\\
\small x^2 & \small =26+10\cos \theta\quad\cdots②\\
\end{split}

①＝②より（どちらも左辺が$\small x^2$なので）、

\begin{split}
\small 14-14\cos \theta & \small =26+10\cos \theta\\
\small \Leftrightarrow \space \cos \theta & \small =-\frac{1}{2}\\
\end{split}

三角比の関係より

\begin{split}
\small \sin^2 \theta & \small +\cos^2 \theta =1\\
\small \sin^2 \theta & \small =1-\left(-\frac{1}{2}\right)^2\\
\small \sin^2 \theta & \small =\frac{3}{4}\\
\small ∴\space \sin \theta & \small =\frac{\sqrt{3}}{2}\\
\end{split}

また、$\small \displaystyle \color{#ff6900}{ \sin (180°-\theta)=\sin \theta}=\frac{\sqrt{3}}{2}$.

よって、求める四角形$\small \mathrm{ABCD}$の面積は、

\begin{split}
\small \mathbf{四角形}\mathrm{ABCD} & \small =\mathrm{△ABD}+\mathrm{△BCD}\\
& \small =\frac{1}{2} \cdot \sqrt{7} \cdot \sqrt{7} \sin\theta +\frac{1}{2} \cdot 1 \cdot 5\sin(180°-\theta) \\
& \small =\frac{7\sqrt{3}}{4}+\frac{5\sqrt{3}}{4} \\
& \small =\color{red}{3\sqrt{3} \space \cdots \mathbf{【答】}}\\
\end{split}

途中で出てきた三角比の角度変換（$\small 180°-\theta$）について公式を忘れていた人は頻出公式_三角比に関する諸公式を確認しておこう。

【問題4】平面図形の応用問題（難易度：★★★★）

問題4：平面図形の応用問題

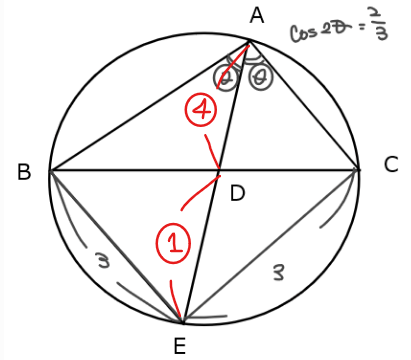
$\small \mathrm{△ABC}$における$\small \angle \mathrm{A}$の二等分線と辺$\small \mathrm{BC}$の交点を$\small \mathrm{D}$とし、$\small \mathrm{A}$から$\small \mathrm{D}$へのばした半直線と$\small \mathrm{△ABC}$の外接円との交点を$\small \mathrm{E}$とする。$\small \angle \mathrm{BAD}$の大きさを$\small \theta$とし、$\small \mathrm{BE}=3$、$\small \displaystyle \cos 2\theta=\frac{2}{3}$とする。このとき、次の各問に答えよ。

(1)線分$\small \mathrm{BC}$の長さを求めよ。
(2)$\small \mathrm{△BEC}$の面積を求めよ。
(3)$\small \mathrm{AD}:\mathrm{DE}=4:1$のとき、線分$\small \mathrm{AB}$、$\small \mathrm{AC}$の長さを求めよ。ただし$\small \mathrm{AB}>\mathrm{AC}$とする。 [宮崎大学]

問題解決のKey

問題文の条件を整理すると下図のようになる。

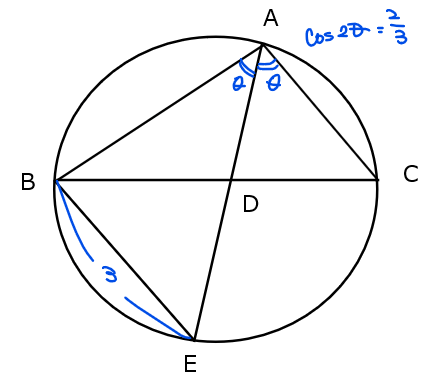
この図からもわかる通り、本問は与えられている情報量が少ないので、図形的な考察から隠れた条件に気づけるかがポイントとなる。
また、$\small (3)$は代数的なアプローチで解く問題となっており、図形的な性質をもとに関係式を立式して解く問題になっている。

　問(1) 解説

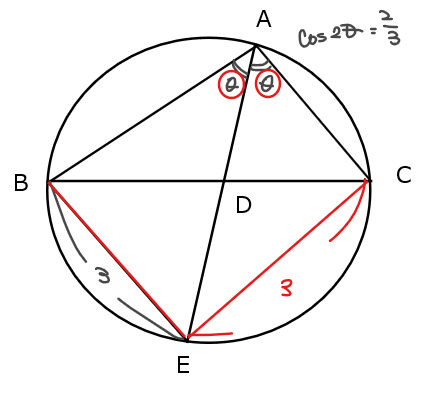
円周角が等しければ弦の長さも等しいので、$\small \mathrm{EC}=\mathrm{BE}=3$。よって、$\small \mathrm{△BEC}$は二等辺三角形。また、円に内接する四角形の対角の和は180°であることから、$\small \angle \mathrm{BEC}=180°-2\theta$。

以上より、線分$\small \mathrm{BC}$の長さは、$\small \mathrm{△BEC}$に対して余弦定理を用いることで、

\begin{split}
\small \mathrm{BC}^2 & \small =3^2+3^2-2\cdot 3\cdot 3\cos (180°-2\theta)\\
& \small =18-18(-\cos 2\theta)\quad \color{#ff6900}{◀ \space \cos(180°-\theta)=-\cos\thetaの利用}\\
& \small =18-18\cdot \left(-\frac{2}{3}\right)\\
& \small =30\\
\end{split}

ゆえに、$\small \mathrm{BC}=\sqrt{30}$…【答】.

　問(2) 解説

三角比の関係より、

\begin{split}
\small \sin \angle \mathrm{BEC}& \small =\color{#ff6900}{\sin (180°-2\theta) }\\
&\small =\color{#ff6900}{\sin 2\theta}\\
&\small =\sqrt{1-\cos^2 2\theta }\\
&\small =\sqrt{1-\left(\frac{2}{3}\right)^2}\\
&\small =\frac{\sqrt{5}}{3}\\
\end{split}

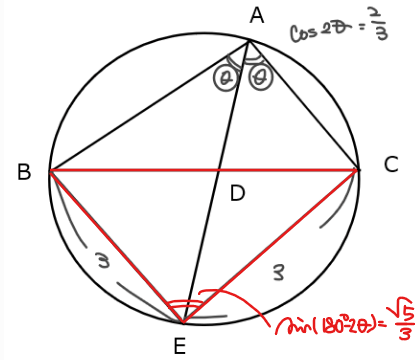
よって、$\small \mathrm{△BEC}$の面積は、

\begin{split}
\small \mathrm{△BEC} & \small = \frac{1}{2}\mathrm{BE}\cdot\mathrm{EC}\sin \angle \mathrm{BEC}\\
&\small =\frac{1}{2}\cdot 3\cdot 3\cdot \frac{\sqrt{5}}{3}\\
& \small = \color{red}{\frac{3\sqrt{5}}{2}\space \cdots\mathbf{【答】}}\\
\end{split}

　問(3) 解説

だいぶ比率が違いますが（ごめんなさい…）、追加された条件を図に表すと上図のようになります。

この条件から、$\small \color{red}{\mathrm{△BEC}:\mathrm{△ABC}=1:4}$であることが分かります。

●OnePoint：面積比の計算
$\small \mathrm{DE}:\mathrm{AD}=1:4$という条件から、$\small \color{blue}{\mathrm{△ABE}}$と$\small \color{red}{\mathrm{△AEC}}$に分けて考えると、底辺の比が面積比【頻出公式No.6】になるので、それぞれ4つの区画の面積は、$\small \color{blue}{\mathrm{△ABE}}$、$\small \color{red}{\mathrm{△AEC}}$を基準として下図のように計算できます。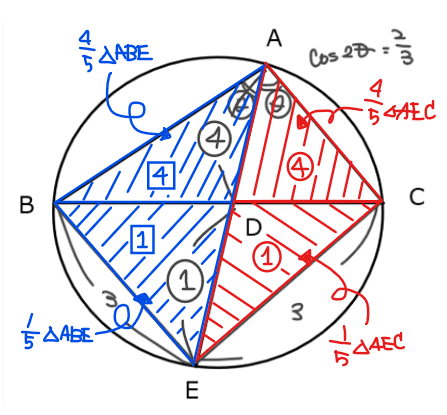

よって、
\begin{cases}
\small \mathrm{△BEC}& \displaystyle \small =\color{blue}{\frac{1}{5}\mathrm{△ABE}}+\color{red}{\frac{1}{5}\mathrm{△AEC}}\\
& \displaystyle \small =\frac{1}{5}(\mathrm{△ABE}+\mathrm{△AEC})\\
\small \mathrm{△ABC}& \displaystyle \small =\color{blue}{\frac{4}{5}\mathrm{△ABE}}+\color{red}{\frac{4}{5}\mathrm{△AEC}}\\
& \displaystyle \small =\frac{4}{5}(\mathrm{△ABE}+\mathrm{△AEC})\\
\end{cases}
となるので、
\begin{split}
&\small \mathrm{△BEC}:\mathrm{△ABC}\\
& \small =\frac{1}{5}(\mathrm{△ABE}+\mathrm{△AEC}):\frac{4}{5}(\mathrm{△ABE}+\mathrm{△AEC})\\
& \small =1:4\\
\end{split}
と求めることができます。

(2)の結果から、$\small \displaystyle \color{red}{\mathrm{△ABC}}=4\times \mathrm{△BEC}=\color{red}{6\sqrt{5}}$と求まる。

$\small \mathrm{AB}=x$、$\small \mathrm{AC}=y$とおく。

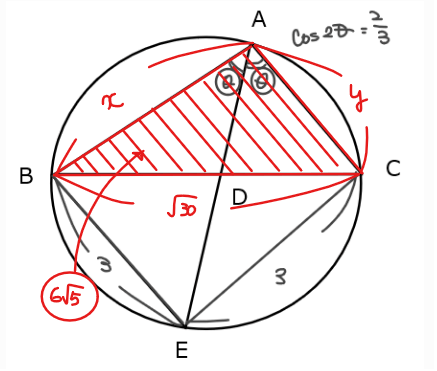
●OnePoint
現時点で分かってる情報を一旦整理すると、上図のように$\small \mathrm{△ABC}$に関して、「面積」と「辺と角」の情報が結構集まっていることに気づく。
このことから、面積に関する公式と、余弦定理（3辺と1角の関係性なので）を用いた立式を検討するのがよさそうだ。

$\small \mathrm{△ABC}$の面積の公式から

\begin{split}
\small \mathrm{△ABC} & \small = \frac{1}{2}\mathrm{AB} \cdot \mathrm{AC} \sin 2\theta\\
\small 6\sqrt{5} &\small =\frac{1}{2}xy\cdot \frac{\sqrt{5}}{3}\\
\small xy& \small = 36 \space \cdots ①\\
\end{split}

また、$\small \mathrm{△ABC}$において余弦定理から

\begin{split}
\small \mathrm{BC}^2 & \small =\mathrm{AB}^2+\mathrm{AC}^2-2\mathrm{AB}\cdot\mathrm{AC}\cos 2\theta\\
\small 30 & \small =x^2+y^2-\frac{4}{3}xy\\
\small 30 & \small =x^2+y^2-\frac{4}{3}\cdot \color{red}{36}\quad \color{red}{◀①を代入}\\
\small x^2 & \small +y^2 =78\quad \cdots ②\\
\end{split}

求める変数が2つで関係式も2本（①、②）なので、あとはゴリゴリ計算を頑張れば解くことができます。ただ、計算はかなり気合が必要です…。

$\small x>0$より、①を$\small \displaystyle y=\frac{36}{x}$として②に代入すると

\begin{split}
\small x^2 & \small +\left(\frac{36}{x}\right)^2 =78\\
\small x^4 & \small -78x^2+36^2=0\\
\small \Rightarrow \space x^2 & \small =39\pm\sqrt{39^2-36^2}\\
\small x^2 & \small =39\pm 15 \color{#ff6900}{\quad ◀ \small 39^2-36^2=(39+36)(39-36)}\\
\small x^2 & \small =54、24\\
\small ∴\space x & \small = 3\sqrt{6}、2\sqrt{6}\\
\end{split}

①より、$\small y$の値は、$\small (x,y)=(3\sqrt{6},2\sqrt{6})、(2\sqrt{6},3\sqrt{6})$。

問題文より、$\small x>y$の条件を加味すると、$\small \mathrm{AB}=3\sqrt{6}$、$\small \mathrm{AC}=2\sqrt{6}$…【答】.

【問題＆解説】空間図形問題

【問題5】正四面体の切り口の面積（難易度：★★）

問題5：正四面体の切り口の面積

1辺の長さが1の正四面体$\small \mathrm{OABC}$がある。辺$\small \mathrm{OA}$の中点を$\small \mathrm{L}$、辺$\small \mathrm{OB}$を$\small 2:1$に内分する点を$\small \mathrm{M}$、辺$\small \mathrm{OC}$を$\small 1:2$に内分する点を$\small \mathrm{N}$とするとき、$\small \mathrm{△LMN}$の面積を求めよ。

問題解決のKey

空間図形の問題は、平面図形に落とし込んで考えるのが定石。
今回であれば、正四面体はすべての面が正三角形の立体であることを利用して、$\small \mathrm{△LMN}$に関する情報を求めていければよいだろう。

　解説

問題文の条件を図式化すると下図の通り。紫色部分が今回求める面積。

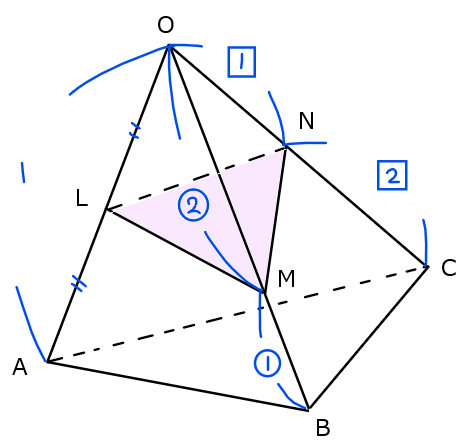
●OnePoint：比の表し方
辺$\small \mathrm{OB}$を$\small 2:1$に内分と言われたら、点$\small \mathrm{O}$から点$\small \mathrm{B}$に向かって、$\small 2:1$となる点に注意。

辺$\small \mathrm{OL}、\mathrm{OM}、\mathrm{ON}$の長さは辺の比から以下の通り。

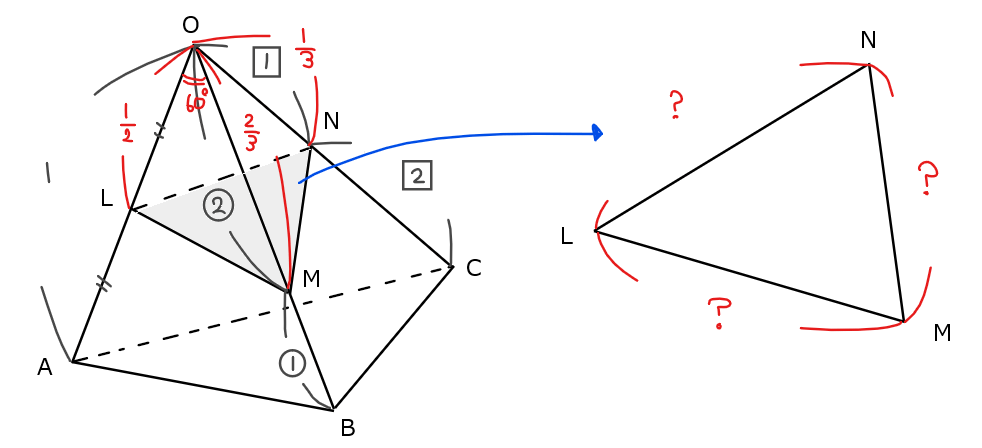
あとは、$\small \mathrm{△LMN}$の面積を求めるために、「2辺とその間の角（$\small \sin$の値）」を求めていく。ただし、いきなりは求まらないので、まずは$\small \mathrm{△LMN}$の3辺の長さを求めていこう。

●辺$\small \mathrm{LM}$
$\small \mathrm{△OAB}$が正三角形（正四面体はすべての面が正三角形）であることから、$\small \angle \mathrm{LOM}=60°$であることに注意して、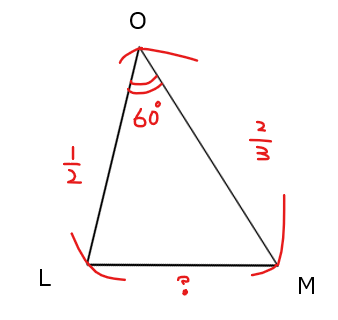

辺$\small \mathrm{LM}$を含む$\small \mathrm{△OLM}$を平面図形として切り出して、余弦定理を用いることで、
\begin{split}
\small \mathrm{LM}^2 &= \small \left(\frac{1}{2}\right)^2+ \left(\frac{2}{3}\right)^2-2\cdot \frac{1}{2}\cdot \frac{2}{3}\cos 60°\\
\small \mathrm{LM}^2 &= \small \frac{1}{4}+\frac{4}{9}-\frac{1}{3}\\
\small \mathrm{LM}^2 &= \small \frac{13}{36}\\
\small ∴\space \mathrm{LM} &= \small \frac{\sqrt{13}}{6}\\
\end{split}

●辺$\small \mathrm{MN}$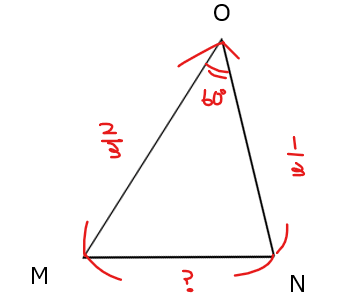

同様に$\small \mathrm{△OMN}$において、余弦定理から
\begin{split}
\small \mathrm{MN}^2 &= \small \left(\frac{2}{3}\right)^2+ \left(\frac{1}{3}\right)^2-2\cdot \frac{2}{3}\cdot \frac{1}{3}\cos 60°\\
\small \mathrm{MN}^2 &= \small \frac{4}{9}+\frac{1}{9}-\frac{2}{9}\\
\small \mathrm{MN}^2 &= \small \frac{1}{3}\\
\small ∴\space \mathrm{MN} &= \small \frac{1}{\sqrt{3}}\\
\end{split}

●辺$\small \mathrm{LN}$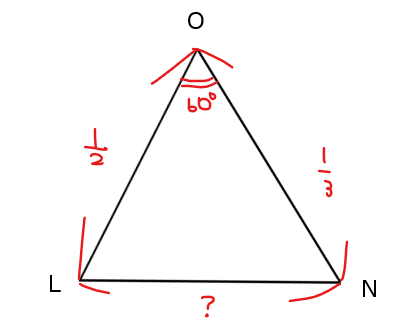

同様に$\small \mathrm{△OLN}$において、余弦定理から
\begin{split}
\small \mathrm{LN}^2 &= \small \left(\frac{1}{2}\right)^2+ \left(\frac{1}{3}\right)^2-2\cdot \frac{1}{2}\cdot \frac{1}{3}\cos 60°\\
\small \mathrm{LN}^2 &= \small \frac{1}{4}+\frac{1}{9}-\frac{1}{6}\\
\small \mathrm{LN}^2 &= \small \frac{7}{36}\\
\small ∴\space \mathrm{LN} &= \small \frac{\sqrt{7}}{6}\\
\end{split}

次は、ここまでで求めた3辺の情報から、どこか1つの角度の余弦を求めていきましょう。どの角でもよいのですが、今回は$\small \cos \angle \mathrm{LNM}$を求めることにします。

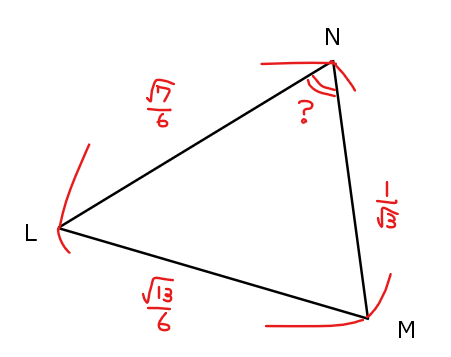
余弦定理より

\begin{split}
\small \left(\frac{\sqrt{13}}{6}\right)^2 = \left(\frac{\sqrt{7}}{6}\right)^2 + \left(\frac{1}{\sqrt{3}}\right)^2 & \small -2\cdot \frac{\sqrt{7}}{6}\cdot \frac{1}{\sqrt{3}}\cos \angle \mathrm{LNM}\\
\small \frac{\sqrt{7}}{3\sqrt{3}} \cos \angle \mathrm{LNM}& \small = \frac{1}{6}\\
\small ∴\space \cos \angle \mathrm{LNM} & \small =\frac{\sqrt{3}}{2\sqrt{7}}\\
\end{split}

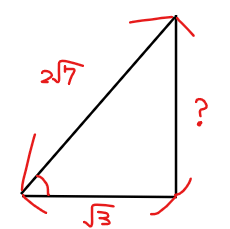
$\small \sin \angle \mathrm{LNM} $は、右図のような直角三角形で考えてあげれば、
$$\small ?=\sqrt{(2\sqrt{7})^2-(\sqrt{3})^2}=5$$
より
$$\small \sin \angle \mathrm{LNM} =\frac{5}{2\sqrt{7}}$$

よって、$\small \mathrm{△LMN} $の面積は、

\begin{split}
\small \mathrm{△LMN} & \small =\frac{1}{2} \mathrm{LN} \cdot \mathrm{MN}\sin \angle \mathrm{LNM} \\
& \small =\frac{1}{2}\cdot \frac{\sqrt{7}}{6} \cdot \frac{1}{\sqrt{3}} \cdot \frac{5}{2\sqrt{7}}\\
& \small =\color{red}{\frac{5\sqrt{3}}{72}\space \cdots \mathbf{【答】}}\\
\end{split}

Point

空間図形の問題は、必ず平面図形に落とし込んで考える！

【問題6】正四面体の体積・垂線（難易度：★★★）

問題6：正四面体の体積と垂線

1辺の長さが2の正四面体$\small \mathrm{OABC}$がある。点$\small \mathrm{O}$から$\small \mathrm{△ABC}$に下した垂線の足を$\small \mathrm{H}$とするとき、以下の問いに答えよ。

(1) $\small \mathrm{OH}$の長さを求めよ。
(2) 正四面体$\small \mathrm{OABC}$の体積を求めよ。
(3) 点$\small \mathrm{H}$から$\small \mathrm{△OBC}$に下した垂線の長さを求めよ。

Point

・求める長さを求めるためにはどんな三角形を切り出せばよいかというセンス磨きも重要。
・点や辺の空間的な位置関係を把握するには、真上・真横などから立体を投影してみるとよい。ある程度のパターンは決まっているため、本問を通して習得していこう。
・(3)は正弦・余弦定理の活用に目が行きがちだが、図形的な性質から解くアプローチも忘れずに。

　（1）解説

問題文の条件を図示すると下図の通り。

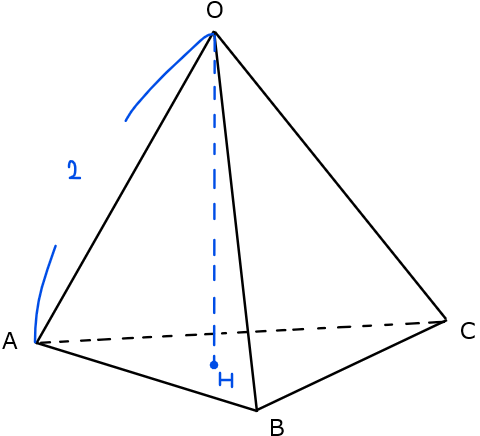
辺$\small \mathrm{OH}$の長さを求めるには、辺$\small \mathrm{OH}$を含む三角形を切り出して平面図形として考えるのが定石となる。

切り出す三角形を考えるために、点$\small \mathrm{H}$の図形的な位置をもう少し詳しく考えてみよう。

正四面体を上から見下ろした投影図を考えると下図の通り。

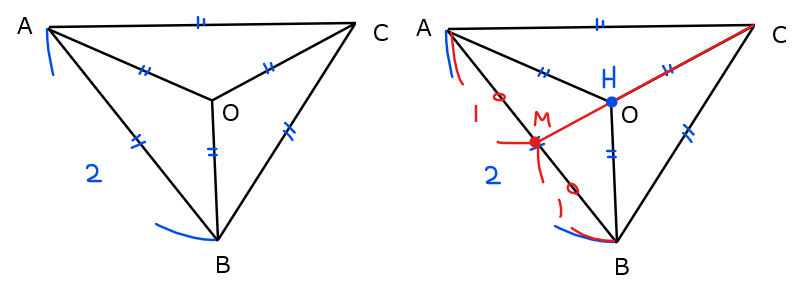
図を見るとわかる通り、点$\small \mathrm{H}$は$\small \mathrm{△ABC}$の中心にあることが分かります。つまり、点$\small \mathrm{H}$は点$\small \mathrm{C}$から辺$\small \mathrm{AB}$に引いた中線上にあるので、辺$\small \mathrm{AB}$の中点を$\small \mathrm{M}$とすると、線分$\small \mathrm{CM}$上の点であることが分かります。

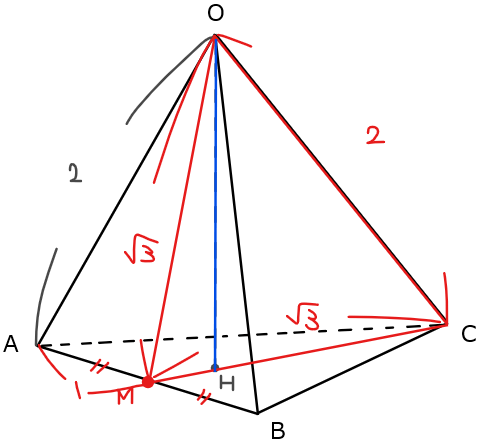
よって、辺$\small \mathrm{OH}$を含む三角形としては$\small \mathrm{△OMC}$を考えればよさそうです。$\small \mathrm{△OMC}$の各辺は、正四面体の各面が1辺2の正三角形であることから、高さ$\small \sqrt{3}$となるので、上図のように求まります。

情報がごちゃごちゃしてきたので、注目したい$\small \mathrm{△OMC}$だけの図に切り出します。ここまで来たら、ただの平面図形の問題ですね。

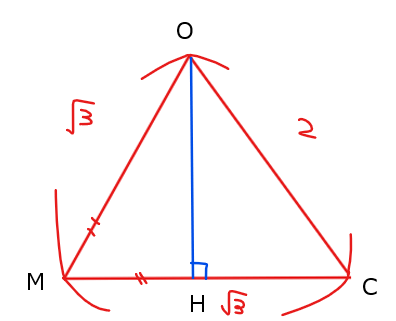
あとは、辺$\small \mathrm{OH}$の求め方はいくつかありますが、3辺が分かっているので、シンプルに$\small \mathrm{△OMC}$の面積を2通りで立式して求める方法ががよさそうです。

●$\small \mathrm{△OMC}$の面積
面積を求めるためにはどこかの正弦（$\small \sin$）が分かってないとダメなので、一旦余弦定理で$\small \cos$を求めて変換します。
\begin{split}
\small \mathrm{OC}^2 & \small = \mathrm{OM}^2+\mathrm{MC}^2-2\cdot\mathrm{OM}\cdot\mathrm{OM}\cos \angle \mathrm{OMC}\\
\small 4 & \small = 6-6\cos \angle \mathrm{OMC}\\
&\small ∴\space \cos \angle \mathrm{OMC} = \frac{1}{3}\\
\end{split}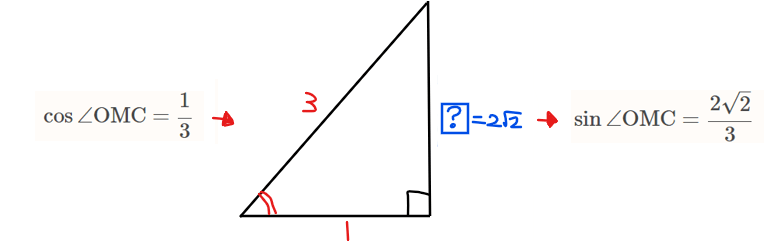
$\small \displaystyle \sin \angle \mathrm{OMC} = \frac{2\sqrt{2}}{3}$より、
\begin{split}
\small \mathrm{△OMC} & \small =\frac{1}{2}\cdot\sqrt{3}\cdot\sqrt{3}\cdot\frac{2\sqrt{2}}{3}\\
\small \mathrm{△OMC} & \small = \sqrt{2}\\
\end{split}

一方で、$\small \mathrm{△OMC} $の面積は、底辺を辺$\small \mathrm{MC}$とみると、高さは線分$\small \mathrm{OH}$になるため、

\begin{split}
\small \mathrm{△OMC} & \small =\frac{1}{2}\cdot \sqrt{3}\mathrm{OH}\\
\small \sqrt{2} & \small =\frac{\sqrt{3}}{2}\mathrm{OH}\\
\small ∴\space \mathrm{OH}& \small =\color{red}{\frac{2\sqrt{6}}{3}\space \cdots \mathbf{【答】}}\\
\end{split}

　（2）解説

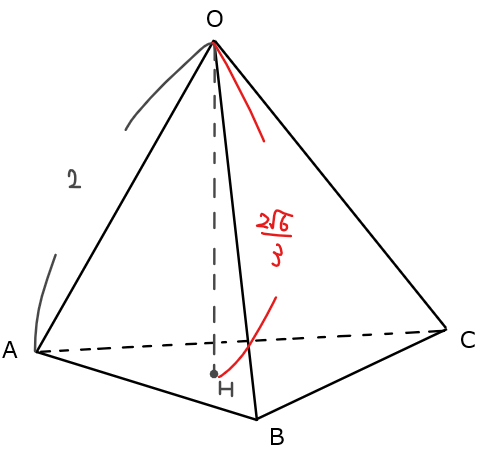
（1）の結果より、正四面体の体積の高さ$\small \mathrm{OH}$は分かっているので、あとは底面 $\small \mathrm{△ABC}$の面積を求めてあげればよい。

●$\small \mathrm{△ABC}$の面積
$\small \mathrm{△ABC}$は1辺が2の正三角形なので、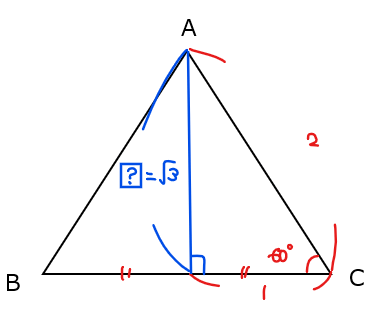

\begin{split}
\small \mathrm{△ABC} & \small = \frac{1}{2}\cdot 2 \cdot \sqrt{3}\\
& \small =\sqrt{3}\\
\end{split}

よって、求める体積を$\small \mathrm{V}$とすると

\begin{split}
\small \mathrm{V}& \small = \frac{1}{3}\cdot\sqrt{3}\cdot \frac{2\sqrt{6}}{3}\\
& \small =\color{red}{\frac{2\sqrt{2}}{3}\space \cdots \mathbf{【答】}}\\
\end{split}

　（3）解説

点$\small \mathrm{H}$から$\small \mathrm{△OBC}$に下した垂線の足を$\small \mathrm{H’}$とおく。

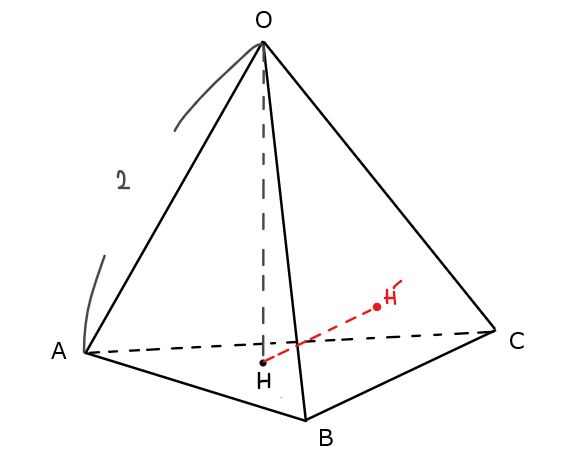
問題文の条件は図示できたが、このままだと点$\small \mathrm{H’}$がどのあたりにある点なのかが分からないので、下図のような補助線を引いてあげると考えやすくなる

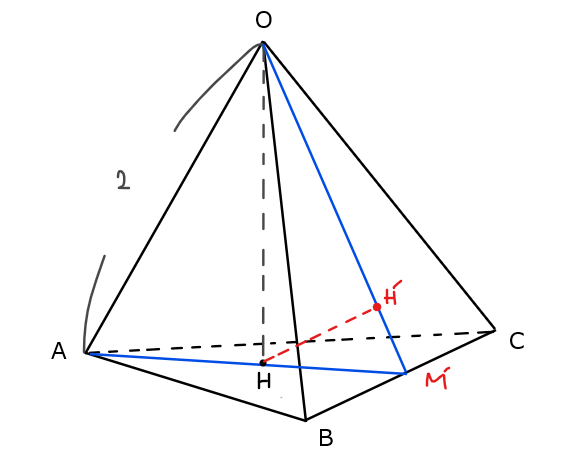
（点$\small \mathrm{M’}$は辺$\small \mathrm{BC}$の中点）。

$\small \mathrm{△OAM’}$を切り出して考えると、求める長さは下図の線分$\small \mathrm{HH’}$になることが分かる。

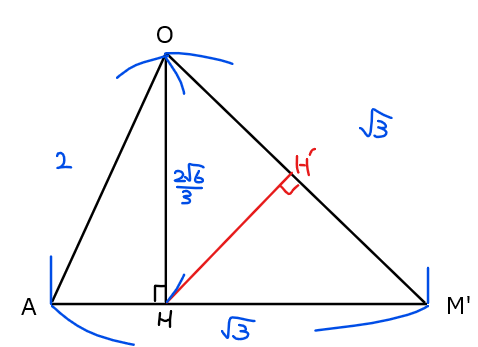
ここで、$\small \mathrm{△OAM’}$は（1）で求めた$\small \mathrm{△OMC}$と同じ形をしているので、

\begin{split}
\small \cos \angle \mathrm{OM’A} = \frac{1}{3} \quad \cdots ①\\
\end{split}

さらに、$\small \mathrm{△OM’H}$と$\small \mathrm{△OHH’}$は、

\begin{split}
& \small \angle \mathrm{M’OH}=\angle \mathrm{HOH’}\space(\mathsf{共通な角})\\
& \small \angle \mathrm{OHM’}=\angle \mathrm{OH’H}=90°\\
\end{split}

より、残りの角も等しくなるので、$\small \angle \mathrm{OM’H}= \angle \mathrm{OHH’} \quad \cdots ②$.

よって、①、②より

\begin{split}
\small \cos \angle \mathrm{OHH’} & \small =\cos \angle \mathrm{OM’A}\quad \color{#ff7043}{◀\angle \mathrm{OM’H}=\angle \mathrm{OM’A}に注意}\\
\small & \small = \frac{1}{3}\\
\end{split}

なので、三角比の定義から

\begin{split}
\small \cos \angle \mathrm{OHH’} & \small =\frac{ \mathrm{HH’}}{ \mathrm{OH}}\\
\small \frac{1}{3}& \small =\frac{\mathrm{HH’}}{ \dfrac{2\sqrt{6}}{3}}\\
\small \mathrm{HH’} & \small = \color{red}{\frac{2\sqrt{6}}{9}\quad \cdots \mathbf{【答】}}\\
\end{split}

【徹底解説】正弦定理と余弦定理の応用問題へのアプローチ

【講義0】図形問題を解く際の心得

これは正弦・余弦定理に限った話ではないので、講義0として最初に記載しますが、図形問題は問題文の条件や求めたことを絶対に図式化しましょう。これが今日のメインといってもよいくらい重要です。

図形問題は他の数学分野と異なり、「視覚的に解く数学」と言えます。たとえば、「実景などをそのまま電波で遠くに送って、映写する装置」と言われても何のことだか分かりにくいですよね？実は、これは「テレビ」の辞書的な説明です。言葉で説明されるよりも、実際にモノを見た方が分かりやすいというわけです。

図形問題も同じで、問題文を図式化してあげることで、多くのヒントを得ることができます。

【講義1】正弦定理と余弦定理の使い分け

図形の問題で多くの人が悩むポイントが、「正弦定理と余弦定理のどちらを使えばよいのか？」だと思います。使い分け方については、おすすめの見極めポイントがあるので一緒に確認していきましょう。

正弦定理を使う問題

●正弦定理を使う問題
・向かい合う辺と角が2組揃っている問題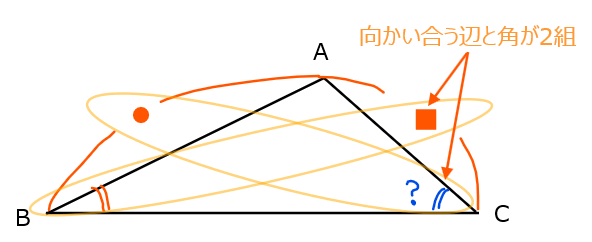

・外接円の半径を求める問題

問題文から既に分かっている辺や角と求める辺や角の関係性が、2組セットで向かい合っている場合は、正弦定理が使えます。逆に言えば、このようなパターンでなければ正弦定理で辺や角を求めることはできないので、余弦定理を使うことになります。

あとは、「外接円」のキーワードが出てきたら正弦定理を使いましょう！

余弦定理を使う問題

●余弦定理を使う問題
・「正弦定理を使う問題」以外の問題

**頻出パターン**
・「2辺とその間の角」の関係になっている問題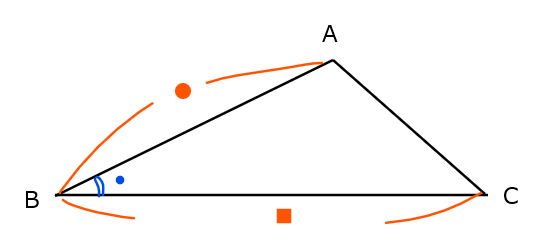

少々雑な説明ですみません…。でも余弦定理が使える問題は非常に多いので、はじめのうちは、基本的には余弦定理を使って解けばいい、と思っていてもよいくらいです。あとは、余弦定理を使って辺や角を求めた後に、正弦定理を使うパターンもあります（もちろん逆もあり）。

【講義02】図形問題で頻出の公式・定理

正弦定理や余弦定理の公式を覚えておくことが大事なことは言うまでもないですが、実は、図形問題を解くには他にも重要な公式や図形的な性質を覚えておく必要があります。

ここでは、図形問題を解く上で絶対に覚えておきたい公式や定理を紹介します。

全部覚えられているか一緒にチェックしてみましょう！

1.余弦定理（重要度：★★★）

●余弦定理
$\small \mathrm{△ABC}$において、
$$ a^2=b^2+c^2-2bc\cos\mathrm{A}$$
※$\small b^2=\cdots$、$\small c^2=\cdots$も同様のため割愛…

図形問題では正直、一番使う頻度が高い公式です。長さや角度を求める問題であればだいたい余弦定理を使うと思っていてもよいくらい。

2.正弦定理（重要度：★★★）

●正弦定理
$\small \mathrm{△ABC}$において、外接円の半径を$\small R$とすると
$$\frac{a}{\sin \mathrm{A}}=\frac{b}{\sin \mathrm{B}}=\frac{c}{\sin \mathrm{C}}=2R$$

余弦定理と並んで重要な公式。辺や角度の計算で利用するほか、外接円の半径を求める場合は必須の公式。あとは、余弦定理がそのまま使えないときに、正弦定理で$\small \sin$を求めて、$\small \cos$に変換してから余弦定理を使うという流れは頻出です。

●OnePoint：分母と分子がどっちが$\small \sin$か覚える方法
公式の両辺では「単位」が同じになることを知っていれば、分母と分子のどちらに$\small \sin$が来るかを知ることができます（物理や化学を履修した人は知ってるかも？？）。

正弦定理の一番右の「$\small 2R$」に着目すると、これは直径なので、単位は「長さ」です。ということは等式ですから、$\small \displaystyle \frac{a}{\sin \mathrm{A}}$なども「長さ」ということになります。

ここで、$\small a$と$\small \sin \mathrm{A}$の単位について考えてみましょう。$\small a$は当然「長さ」です。$\small \sin \mathrm{A}$は「三角比」という名前の通り比なので、単位はありません。

このことから、$\small a$が分子、$\small \sin \mathrm{A}$が分母だと分かります（逆にしてしまうと、分母に長さが来てしまいおかしなことになります）。

なので、「長さが上にくる！」と覚えておきましょう。

3.三角比に関する諸公式（重要度：★★★）

●三角比の関係式
\begin{split}
&\sin^2 \theta +\cos^2 \theta =1\\
\end{split}
・$\small \sin$と$\small \cos$の変換で利用する公式です。

●角度に関する三角比の関係式
\begin{split}
&\sin(180°-\theta)=\sin \theta\\
&\cos(180°-\theta)=-\cos \theta\\
\end{split}
・円に内接する四角形の問題で必須の公式です。

4.三角形の面積を求める公式（重要度：★★★）

●三角形の面積を求める公式
$\small \mathrm{△ABC}$の面積を$\small \mathrm{S}$とすると
$$\mathrm{S}=\frac{1}{2}ab\sin \mathrm{C}$$
※$\small a,b,c$を入れ替えても成り立つので他は割愛…
・純粋に面積を求める問題以外にも、面積の関係式から辺の長さを求める問題でも重宝します。

5.角の二等分線の性質（重要度：★★）

●角の二等分線の性質
$\small \mathrm{△ABC}$において、$\small \mathrm{\angle A}$の二等分線と辺$\small \mathrm{BC}$の交点を$\small \mathrm{D}$としたときに、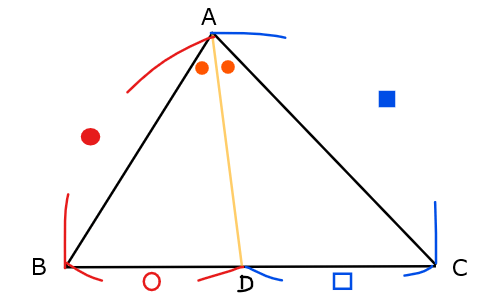

$$\mathrm{AB}:\mathrm{AC}=\mathrm{BD}:\mathrm{DC}$$
・角の二等分線が出てきたら、この公式を使って辺の長さを求める可能性大

6.高さ共通の三角形の面積比（重要度：★★）

●高さ共通の三角形の面積比
高さが同じ三角形では、底辺の比＝面積比となる。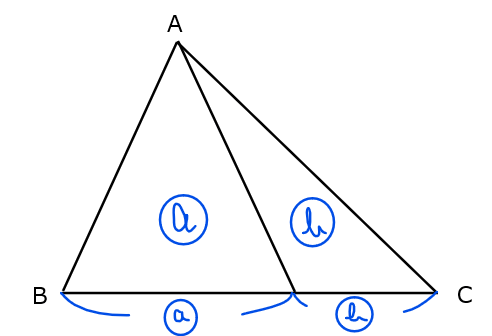

・面積比を使って面積を求める問題が頻出

7.円に内接する四角形の性質（重要度：★★）

●円に内接する四角形の性質
円に内接する四角形の対角の和は180°
・角度に関する三角比の関係式とセットでよく使う

おまけ

図形の分野では、今回紹介した公式以外にも、参考書の付録や証明問題などで紹介される公式が意外と多くあります。

「トレミーの定理」や「ヘロンの公式」といったかっこいい名前の公式から、名前もついていないような公式まで様々な公式がでてきますが、ここで気になるのが「この公式って覚えた方がいいのか？」ですよね？

結論、こういった公式は覚えなくて大丈夫です！なぜなら、使わないからですね（笑）。例えば角の二等分線に関する公式として以下があります。

●角の二等分線に関する公式
$\small \mathrm{△ABC}$において、$\small \mathrm{\angle A}$の二等分線と辺$\small \mathrm{BC}$の交点を$\small \mathrm{D}$としたときに、
$$\small \mathrm{AD}^2=\mathrm{AB}\cdot \mathrm{AC}-\mathrm{BD}\cdot \mathrm{DC}$$

この公式を覚えていれば、本記事の問題2を割と簡単に求めることができますが、ほぼほぼ使う機会がないので、暗記してもコスパが悪いです…。

他の公式も大半が複雑で覚えにくいのに利用頻度も低いというメリット感ゼロの公式なので、その公式を覚える時間があったら、他の図形問題の演習をした方がよっぽど学習効率が高いと思います。

本記事のまとめ

今回は正弦定理・余弦定理を利用した平面図形・空間図形の問題を解説してみました。基本問題から入試レベルの問題まで扱いましたが、図形問題は視覚からヒントを得られることが非常に多いので、しっかりと問題文の条件を図に描いて、ひらめけるようにしましょう。

最後に今回のポイントを簡単に振り返っておきましょう。

個人的には、図形問題はつまずいた箇所が苦手な考え方だったり、発想の転換が必要なポイントだったりするので、正弦定理、余弦定理を使う問題、比や図形的性質から解く問題、いろいろな問題を演習して解ける問題を増やしていきましょう！

では、今回はここまでです。お疲れ様でした！