今回は、確率の最大値を求める問題について徹底解説していきます。
よく参考書などで、確率の最大値を求める方法として、「\(\small \displaystyle \frac{p_{n+1}}{p_n}\)と1の大小を比較しましょう」であったり、「\(\small p_{n+1}-p_n\)と0の大小を比較しましょう」といった解法がありますが、どうしてこの方法で確率の最大値が求まるのか疑問を抱いている人は少なくないでしょう。
本記事では、この疑問を解消するため、確率の最大値を求めるための考え方について、頻出問題(さいころ問題/カード問題)を用いてわかりやすく解説していきますので、ぜひ最後までチェックしてみてください!
- 確率の最大値の求め方が分からない人
- \(\small \displaystyle \frac{p_{n+1}}{p_n}\)と\(\small 1\)や\(\small p_{n+1}-p_n\)と\(\small 0\)で大小比較する理由が分からない人
- 確率の最大値を求める方法はいろいろあるけど、結局どのように解くのが簡単なのかを知りたい人
本記事の要点
今回は確率の最大値を求める問題について解説していきますが、はじめに本記事の結論をお伝えします。
☆重要Point☆
・確率の最大値は、『大小関係の転換点』という感覚を理解しよう。
・確率が最大となる値は1箇所とは限らない!
では、上記の結論をもとに、問題を通して理解を深めていきましょう。
【問題&解説】確率の最大値を求める問題
【問題1】反復試行の確率の最大値(さいころ問題)
さいころを\(\small 100\)回投げて\(\small 6\)の目がちょうど\(\small n\)回出る確率を\(\small p_n\)とするとき、\(\small p_n\)が最大値となるときの\(\small n\)の値を求めよ。ただし、\(\small 0≦n≦100\)とする。
[類 慶応大]
\begin{split}
& \small p_1<p_2< \cdots \color{red}{p_{k-1}<p_k>p_{k+1}}>\cdots
\end{split}
ということ。なので、\(\small p_k\)の前後の確率との大小比較を行えばよい(詳細は講義1参照)。
問題文の確率 \(\small p_n\)は、\(\small n\)回6の目が出て、\(\small 100-n\)回は6以外の目が出るということなので、
\begin{split}
\small p_n & \small = {}_{100} \mathrm{C}_n \left(\frac{1}{6}\right)^n \left(\frac{5}{6}\right)^{100-n}\\
& \small = {}_{100} \mathrm{C}_n \frac{5^{100-n}}{6^{100}}\\
\end{split}
ここで、\(\small p_n\)が最大になるときの\(\small n\)の値を\(\small k\)とします。つまり、\(\small n=k\)で確率が最大値 \(\small p_k\)になるとします。
このとき、確率 \(\small p_k\)が最大になるとは、
\begin{split}
\small p_0< p_1< \cdots \color{red}{ p_{k-1}<p_k>p_{k+1}}>\cdots>p_{100}
\end{split}
を満たす\(\small p_k\)を求めることなので、
\begin{cases}
\small p_{k-1} < p_k \space(1≦k≦100) \quad \cdots①\\
\small p_{k} > p_{k+1} \space(0≦k≦99) \quad \cdots②\\
\end{cases}
で、①かつ②を満たす条件を考えればよい。
●OnePoint
条件式①、②を変形して
\begin{cases}
\small 1 < \dfrac{p_k}{p_{k-1}} \quad (①から)\\
\small 1 >\dfrac{p_{k+1}}{p_{k}} \quad(②から)\\
\end{cases}
としたものが、よく参考書で紹介されている分数と1を大小比較する方法です。
本解説ではわかりやすさのため①、②の条件式を用いるが、結局分数にしているか否かの違いなので、解き方としては変わらないと思ってもらっても大丈夫です。
本解説の解法は講義2で詳しく解説しているので併せて確認してみましょう。
【条件①】\(\small p_{k-1} < p_k\)(\(\small 1≦k≦100\))
\begin{split}
& \small {}_{100} \mathrm{C}_{\color{red}{k-1}} \frac{5^{100-(\color{red}{k-1})}}{6^{100}} < {}_{100} \mathrm{C}_{\color{red}{k}} \frac{5^{100-\color{red}{k}}}{6^{100}} \\
\Leftrightarrow \space & \small \frac{100\times \cdots \times (100-(k-1)+1)}{(k-1)!} \times 5^{101-k}\\
& \small < \frac{100\times \cdots \times (100-k+1)}{k!} \times 5^{100-k}\\
\Leftrightarrow \space & \small \frac{\color{magenta}{100\times \cdots \times (102-k)}}{\color{#ff5521}{(k-1)!}} \times \color{#00AB06}{5^{100-k}} \times 5\\
& \small < \frac{\color{magenta}{100\times \cdots \times (102-k) }\times (101-k)}{\color{#ff5521}{(k-1)!}\times k} \times \color{#00AB06}{5^{100-k}}\\
\Leftrightarrow \space & \small 5< \frac{101-k}{k} \quad \color{red}{◀\mathsf{共通部分(同色箇所)を約分}}\\
\Leftrightarrow \space & \small 5k<101-k\\
\Leftrightarrow \space & \small k<\frac{101}{6}=16.83\cdots\\
\end{split}
ゆえに、\(\small 1≦k≦16 \space \cdots①’\) (\(\small k\)は回数=自然数のため、16以下と考えて問題ない)
★重要★
\(\small 1≦k≦16\)で条件①の\(\small p_{k-1} < p_k\)が成り立つということは、具体的な不等式でかくと、
が成り立つということ。
【条件②】\(\small p_{k} > p_{k+1} \)(\(\small 0≦k≦99\))
\begin{split}
& \small {}_{100} \mathrm{C}_{\color{red}{k}} \frac{5^{100-\color{red}{k}}}{6^{100}} >{}_{100} \mathrm{C}_{\color{red}{k+1}} \frac{5^{(100-\color{red}{k+1})}}{6^{100}} \\
\Leftrightarrow \space & \small \frac{100\times \cdots \times (100-k+1)}{k!} \times 5^{100-k}\\
& \small > \frac{100\times \cdots \times (100-(k+1)+1)}{(k+1)!} \times 5^{100-(k+1)}\\
\Leftrightarrow \space & \small \frac{\color{magenta}{100\times \cdots \times (101-k)}}{\color{#ff5521}{k!}} \times \color{#00AB06}{5^{99-k}}\times 5 \\
& \small > \frac{\color{magenta}{100\times \cdots \times (101-k)}\times (100-k)}{(k+1) \color{#ff5521}{\times k!}} \times \color{#00AB06}{5^{99-k}}\\
\Leftrightarrow \space & \small 5> \frac{100-k}{k+1} \quad \color{red}{◀\mathsf{共通部分(同色箇所)を約分}}\\
\Leftrightarrow \space & \small 5k+5>100-k\\
\Leftrightarrow \space & \small k>\frac{95}{6}=15.83\cdots\\
\end{split}
ゆえに、\(\small 16≦k≦99 \space \cdots②’\) (同様に、\(\small k\)が自然数なので、15.83より大きな自然数ということは、実質16以上ということ)
★重要★
同様に、\(\small 16≦k≦99\)で条件②の\(\small p_{k} > p_{k+1}\)が成り立つということは、
が成り立つということ。
確率が最大になる条件は、①’、②’の両方を満たす\(\small k\)の範囲を求めればよいので、\(\small k=16\)。
実際に、①、②、①’、②’の条件を書き出すと
\begin{cases}
\small ①\space →\space p_0<p_1<\cdots <p_{15}<p_{16}\\
\small ②\space →\space p_{16}>p_{17}>\cdots p_{99}>p_{100}\\
\end{cases}
となるので、2つの不等式を組み合わせると
$$\small p_0<p_1<\cdots <p_{15}<\color{red}{p_{16}}>p_{17}>\cdots p_{99}>p_{100}$$
となり、\(\small p_{16}\)で確率が最大になることが分かる。
よって、確率が最大となるときの\(\small n\)の値は、\(\small n=16\) …【答】。
【問題2】組み合わせ問題の確率の最大値(N枚のカード)
箱の中に1番から\(\small N\)番までの番号札が1枚ずつ合計\(\small N\)枚入っている。この箱から同時に4枚の番号札を取り出す。この4枚の中で、最小の番号が3である確率を\(\small P_{N}\)とする。ただし、\(\small N≧6\)とする。
(1) \(\small P_N\)を求めよ。
(2) \(\small P_N\)を最大にする\(\small N\)とその最大値を求めよ。
[宮城教育大]
求める確率\(\small P_N\)は、\(\small N\)枚の番号札の中から4枚を同時に選んだときに、3番が一番小さくなっている確率。「同時に」のキーワードがあるので、組み合わせになります。

全体パターンの通り数は、\(\small N\)枚から4枚を選ぶ組み合わせなので、\(\small \color{red}{ {}_N \mathrm{C}_4}\)通り。
そのうち、一番小さい番号札が3である通り数は、3番があるのは確定(=1通り)で、1~3以外、すなわち、\(\small 4~N\)番までの\(\small N-3\)枚の中から3枚を選べばよいので、\(\small {}_{N-3} \mathrm{C}_{3} \)通り。
よって、
\begin{split}
\small P_N & \small = \frac{{}_{N-3} \mathrm{C}_3}{{}_N \mathrm{C}_4}\\
& \displaystyle \small = \frac{\dfrac{(N-3)(N-4)(N-5)}{3!}}{\dfrac{N(N-1)(N-2)(N-3)}{4!}}\\
& \displaystyle \small = \color{red}{\frac{4(N-4)(N-5)}{N(N-1)(N-2)}\quad \cdots \mathbf{【答】}}\\
\end{split}
●確率は組み合わせか順列かを意識しよう
・「同時に」とあれば組み合わせ
・「順番が重要」であれば順列
\(\small P_N\)が最大になるときの\(\small N\)を\(\small k\)とすると、確率の最大値\(\small P_k\)は\(\small N≧6\)より、
\begin{cases}
\small P_{k-1} < P_k \space(7≦k) \quad \cdots①\\
\small P_{k} > P_{k+1} \space(6≦k) \quad \cdots②\\
\end{cases}
この①と②の2つの条件をともに満たす\(\small k\)が求まればよい。
【条件①】\(\small P_{k-1} < P_k \space(7≦k)\)
(1)の答えに\(\small N=k-1、k\)をそれぞれ代入することで、
\begin{split}
& \small \frac{4((k-1)-4)((k-1)-5)}{(k-1)((k-1)-1)((k-1)-2)} < \frac{4(k-4)(k-5)}{k(k-1)(k-2)}\\
& \small \Leftrightarrow \space \frac{4(k-5)(k-6)}{(k-1)(k-2)(k-3)} < \frac{4(k-4)(k-5)}{k(k-1)(k-2)}\\
& \small \Leftrightarrow \space \frac{k-6}{k-3} < \frac{k-4}{k}\\
& \small \Leftrightarrow \space k^2-6k < k^2-7k+12\\
& \small \Leftrightarrow \space k < 12\\
\end{split}
よって、\(\small 7≦k<12\)、すなわち \(\small 7≦k≦11\)のとき、\(\small P_{k-1} < P_k \)が成立するので、
$$\small \color{red}{P_7<P_8<\cdots <P_{10}<P_{11}\quad \cdots ①}$$
【条件②】\(\small P_{k} > P_{k+1}\)(\(\small 6≦k\))
同様に、(1)の結果を適用することで
\begin{split}
& \small \frac{4(k-4)(k-5)}{k(k-1)(k-2)} > \frac{4((k+1)-4)((k+1)-5)}{(k+1)((k+1)-1)((k+1)-2)}\\
& \small \Leftrightarrow \space \frac{4(k-4)(k-5)}{k(k-1)(k-2)} > \frac{4(k-3)(k-4)}{(k+1)k(k-1)}\\
& \small \Leftrightarrow \space\frac{k-5}{k-2} > \frac{k-3}{k+1}\\
& \small \Leftrightarrow \space k^2-4k-5 > k^2-5k+6\\
& \small \Leftrightarrow \space k >11\\
\end{split}
よって、\(\small k\)は自然数なので、実質 \(\small k≧12\)の範囲で、\(\small P_{k} > P_{k+1}\)が成立することから、
$$\small \color{red}{P_{12}>P_{13}>\cdots\quad \cdots ②}$$
以上の①、②の結果を整理すると\(\small N≧7\)の\(\small P_N\)の大小関係は、
$$\small P_7<P_8<\cdots <P_{10}<P_{11}\space \color{red}? \space P_{12}>P_{13}>\cdots$$
となり、\(\small P_{11}\)と\(\small P_{12}\)の大小関係が不透明になっている。なので、ここからは\(\small P_{11}\)と\(\small P_{12}\)の具体的な値を計算して大小関係を確かめてみよう。
\begin{split}
\small P_{11} &\small = \left. \frac{4(N-4)(N-5)}{N(N-1)(N-2)}\right|_{N=11}\\
& \small =\frac{4\times 7\times 6}{11 \times 10 \times 9}\\
& \small =\color{red}{\frac{28}{165}}\\
\end{split}
\begin{split}
\small P_{12} &\small = \left. \frac{4(N-4)(N-5)}{N(N-1)(N-2)}\right|_{N=12}\\
& \small =\frac{4 \times 8 \times 7}{12 \times 11 \times 10}\\
& \small =\color{red}{\frac{28}{165}}\\
\end{split}
このことから、\(\small \color{red}{P_{11}=P_{12}}\)であることかが分かる。
つまり、確率の大小関係は、
$$\small P_7<P_8<\cdots <P_{10}<\color{red}{P_{11}=P_{12}}>P_{13}>\cdots$$
となることが分かったので、問題への解答としては、\(\small N=11、12\)で最大値 \(\small \displaystyle \frac{28}{165}\)…【答】。
【徹底解説】確率の最大値の求め方
【講義1】確率が最大とは
確率の最大値を求めるときに、以下のような解法を目にしたことはありませんか?
・\(\small \displaystyle \frac{p_{n+1}}{p_n}\)と1を大小比較する解法
・\(\small p_{n+1}-p_n\)と0を大小比較する解法
「なんで大小比較すると最大値が求まるの?」と疑問に思った人は、本講義を確認しておきましょう。
確率の最大値=大小関係の転換点
\begin{split}
\small p_1< p_2< \cdots \color{red}{ p_{k-1}< p_k > p_{k+1}}>\cdots
\end{split}
を満たすこと。
不等式で書かれると若干分かりにくいかもしれませんが、この関係式が超重要です!
●関係式の意味
関係式の意味を日本語化すると、\(\small p_1、p_2、\cdots\)とどんどん確率が大きくなっていき、\(\small p_k\)を境に今度は確率が小さくなっていくということを表しています。

このことから、確率が最大になるのは、大小関係の転換点であることが分かります。
大小比較で最大値が判定できる理由
確率の最大値を求める問題の解説では、冒頭で紹介したような \(\small \displaystyle \frac{p_{k+1}}{p_{k}}\)と1の大小比較をよく見かけます。では、この大小比較からどんなことが分かるのかを一緒に確認していきましょう。
●大小比較で分かること
・\(\small \displaystyle \frac{p_{k+1}}{p_{k}}<1\)の大小比較
式変形すると \(\small \displaystyle \color{red}{p_{k}>p_{k+1}}\)となるので、最大値 \(\small p_k\)が分かる。
・\(\small \displaystyle \frac{p_{k+1}}{p_{k}}=1\)の大小比較
式変形すると、\(\small \color{red}{p_{k}=p_{k+1}}\)となるので、最大値が\(\small p_k、p_{k+1}\)の2つ存在するか否かが分かる。
・\(\small \displaystyle \frac{p_{k+1}}{p_{k}}>1\)の大小比較
式変形すると、\(\small \displaystyle \color{red}{p_{k}<p_{k+1}}\)となるので、最大値 \(\small p_{k+1}\)が分かる。
このように、\(\small \displaystyle \frac{p_{k+1}}{p_{k}}\)と1の大小比較をすることで、大小関係の転換点を求めているわけです。そのため、この方法で確率の最大値を求めることができます。
最大値は1つとは限らない
冒頭で確率の最大値は大小関係の転換点であることを不等式を用いて説明しました。冒頭の例では最大値は1つだけでしたが、必ずしも1つとは限らないので注意が必要です。

上記の \(\small p_k=p_{k+1}\)のようにたまに折り返し地点がちょうど同じ値になることがあります。この時は最大値は \(\small p_k、p_{k+1}\)の2つになることを覚えておきましょう。
【深堀】大小比較で最大値が求まることの数学的導出
ここでは、本講義の最初に紹介した関係式
$$\small p_1<p_2<\cdots <p_{k-1}<p_{k}>p_{k+1}>\cdots$$
から、\(\small \displaystyle \frac{p_{k+1}}{p_{k}}\)と1の大小関係が導出できるという話をします。細かい話になるので、興味があれば読んでみてください。
問題を解く上では知らなくても大丈夫な内容なので、「もうおなかいっぱい…」という人は読み飛ばしてしまって大丈夫です!
では早速解説していきます。
まず、以下の赤枠の大小関係①を考えることで

\begin{split}
&\small p_{k-1}<p_k\\
&\Leftrightarrow \space \small 1<\frac{p_{k}}{p_{k-1}}\space(k≧2)\\
&\Leftrightarrow \space \small \color{red}{1<\frac{p_{k+1}}{p_{k}}}\space(k≧1)\quad \cdots①\\
\end{split}
●補足:数字の添え字に意味はない!
数学ではよくある変形ですが、2行目から3行目への式変形は、\(\small p_k\)の添え字\(\small k\)を\(\small k+1\)に1つプラスしています。その代わりに、\(\small k≧2\)という条件を\(\small k≧1\)に変換しています。両方とも具体的に\(\small k\)に値を代入すると同じ式であることが分かります(2行目の\(\small k=2\)と3行目の\(\small k=1\)は、いずれも\(\small \displaystyle 1<\frac{p_2}{p_1}\)で同じ値になる)。
同様に青枠の大小関係②を考えることで、
\begin{split}
&\small p_{k}>p_{k+1}\\
&\Leftrightarrow \space \small \color{red}{1>\frac{p_{k+1}}{p_{k}}}\quad \cdots②\\
\end{split}
あとは、関係式にはないのですが、特殊パターンとして、\(\small \displaystyle p_k=p_{k+1} ⇔ \color{red}{\frac{p_{k+1}}{p_k}=1}\space \cdots③\)となるパターンもあります。ちょうど山の折り返しが同じ値になるパターンですね。
①~③をまとめると結局、\(\small \displaystyle \frac{p_{k+1}}{p_{k}}\)が1より大きいのか小さいのかイコールなのかを調べればよいので、大小比較で最大値が求まることになります。
ちなみに、\(\small p_{k}>p_{k+1}\)の関係式を先程は\(\small p_{k}\)で割り算して分数にしましたが、\(\small p_{k+1}-p_{k}<0\)のように移項すると0との比較になり、同様に導くことができますが、ここでは解説は割愛します。
【講義2】確率の最大値の求め方(おすすめ)
一般的な確率の最大値の求め方は講義1で紹介した\(\small \displaystyle \frac{p_{k+1}}{p_{k}}\)と1の大小比較をする方法です。
ここからは、個人的なおすすめの解き方を紹介します。本質的には同じ考え方なのですが、こちらの方が考え方が分かりやすい点がメリットになります。
STEP2:減少領域(\(\small p_{k}>p_{k+1}\))が成り立つ範囲を求める
STEP3:増加領域と減少領域を合わせた範囲が確率の最大点
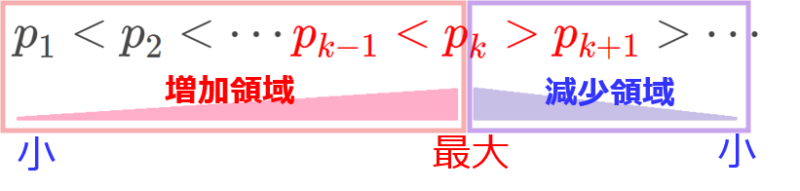
STEP1で確率が増加する範囲をもとめ、STEP2で逆に確率が減少する範囲を求めます。すると、途中までは確率が増加する一方で、ある時点から確率が減少することになります。この大小関係の転換点が確率の最大値というわけです。
もう少しイメージが湧くように具体例で考えてみます。
例えば、確率の大小関係 \(\small p_k<p_{k+1}\)(\(\small =\)増加領域)が\(\small 1≦k≦3\)の範囲で成り立つとします。一方で、 \(\small p_k>p_{k+1}\)(\(\small =\)減少領域)が\(\small 4≦k≦5\)の範囲で成り立つとします。この状況を書き出すと以下のようになります。
・増加領域:\(\small p_1<p_2<p_3<p_4\cdots①\)
・減少領域:\(\small p_4>p_5>p_6\cdots②\)
●OnePoint
増加領域の関係式は、\(\small p_k<p_{k+1} \)に\(\small k=1、2、3\)をそれぞれ代入すると、\(\small p_1<p_2、p_2<p_3、p_3<p_4\)となることから導ける(減少領域についても同様)。
最後にSTEP3として①,②を組み合わせることで、\(\small p_1<p_2<p_3<p_4>p_5>p_6\)となり、\(\small p_4\)が確率の最大値と求まります。
この3STEPでどんな問題でも確率の最大値を求めることができるので、本記事の問題を通して3STEPの使い方をしっかり理解しておきましょう。
本記事のまとめ
今回は確率の最大値の求め方について徹底解説していきましたが、いかがでしたか?参考書でおなじみの\(\small \displaystyle \frac{p_{k+1}}{p_{k}}\)と1を大小比較する意味が理解できたでしょうか?ちょっと、怪しいなと思った人は改めて講義1を再確認しておきましょう。
最後に改めて今回の重要Pointを振り返っておきましょう。
☆重要Point☆
・確率の最大値は、『大小関係の転換点』という感覚を理解しよう。
・確率が最大となる値は1箇所とは限らない!
今回はここまです。お疲れ様でした!








コメント