今回は、高校数学で初めに出てくる新概念といっても過言ではない、「三角比」について解説していきます。皆さんも一度は聞いたことがあるサイン、コサイン、タンジェントってやつです。なんだったっけ?と思った人はぜひ最後まで読んでみてください!
はじめに
皆さんは三角比って何か説明できますか?「サインとかコサインのことでしょ?」って思っている人は確かにそうなんですが、そもそもサインやコサインって何のために考え出されたものでしょうか?三角比の目的や意義って何なのか説明できますか?
こんな質問をされると意外とよくわかってないかも、と思った人も多いのではないでしょうか?今回は、三角比の定義を紹介するとともに、三角比にどんな意味があるのかを分かりやすく解説してきます。「三角比が何なのか理解したい!」、「三角比がどんな理由で作り出されたのか興味がわいてきた!」、「三角比が身の回りの日常生活でどんなふうに使われているのか知りたい!」という人はこの記事で一緒に確認していきましょう!
【前提知識】「比」とは?
三角比について説明するためには、前提知識として「比」について理解を深めておく必要があります。ちょっと長くなりますが、これが理解できていないと三角比の説明が最初から頭に入ってこなくなってしまうのでまずは比について確認していきましょう。
比の表し方
比というのは漢字からもわかるように「何かと何かを比べる」という意味です。比べる2つのものをどう表すかによって、比の表し方は通常2パターンあります。
記号を使った比の表し方
1つ目は、「\(\small a:b \)」のように、比べたい2つを「:(コロン)」を使って比較するパターンで、多くの人が一番初めに思いついたのではないでしょうか。ちなみに3つ以上の比を表したい場合は、\(\small a:b:c\)と表記することもあります。
分数を使った比の表し方
2つ目は、「\(\small \frac{a}{b}\)」のように、分数で表すパターンです。分数で表せるということは意外と知られてなかったりします。
でも実は、もともと比は分数で表していました。しかし、分数だと3つ以上のものを比べるときに表現ができなくなるので、「\(\small \frac{a}{b}=a÷b → a:b\)」のように割り算の記号「÷」から中央の線を消した記号を比を表す記号にしようと決めたんです。なので比を表すときは「:」を使うと学校では教わるので、逆に分数で比を表わすというもともとの方が知られなくなってしまいました。
なので、「比=分数」ということをまずは覚えておきましょう!
でも、具体的にどうやって分数で比を表すのかピンと来てない人もいると思うので、具体例で解説します。たとえば、料理をするときに「水1/2カップ」というような説明を見たことがあると思います。これがまさに分数を使った比です。「\(\small \frac{1}{2}\)」という分数が、「1カップに対して1/2の水を入れてください」ということを表現しているわけです。
比を使うメリット
最後に、比を使うメリットについて説明します。さっきの料理の例であれば、「わざわざ比なんて使わなくても、水1/2カップならば具体的に水100ml(日本では1カップ=200ml)って書いた方が早くない?」と思う人もいるかもしれません。
あえて比を使って書くことのメリットは2つあると思います。1つ目は、基準が違っても対応できること、2つ目は、ざっくりイメージを伝えられることです。順番に説明していきますね。
【メリットその1】基準が違っても対応できる
料理の例の1カップというのは実は国によって量が異なるようで、日本では200ml、アメリカでは240ml、オーストラリアなどでは250mlだそうです。また、水のような液体の場合は上記の分量になりますが、お米の場合は1カップは180mlというように同じ1カップでも量が変わります。
このように国や計るものの種類によって具体的な量が異なる場合、レシピに「日本の人は200ml、アメリカの人は240ml入れてください!」なんて書いたら記載がごちゃごちゃしてわかりにくいですし手間ですよね?でも、あらかじめ1カップという基準を決めてしまいその分量を基準に「何カップなのか」を表す方が分かりやすいですし手間も省けます。
具体例でいうと、1カップに対して2倍の量なら2カップ、半分の半分なら1/4カップみたいな感じです。
このように基準をもとにどのくらいかを表すときに分数=比が大活躍するわけです。
【メリットその2】ざっくりイメージを伝えられる
比はイメージを伝えるときに便利です。例えば、テレビのサイズには大きく2種類があります。では次の説明のうちどちらの方がイメージが湧きますか?
【説明1】
1種類目は、縦が1525mm、横が2033mm、2種類目は、縦が1246mm、横が2215mmです。
【説明2】
1種類目は、縦横比が4:3、2種類目は、縦横比が16:9です。
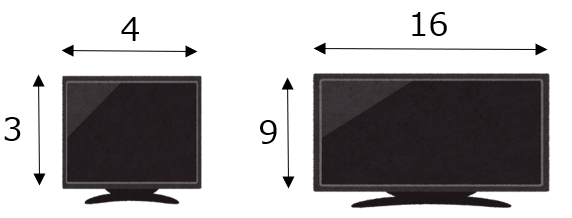
どうでしょうか?多くの人が「説明2」の方がテレビの形のイメージが湧いたのではないでしょうか?理由は、比を使った説明の方が画面の形が分かりやすいからです。形をイメージするときには縦横の長さが具体的にどんな長さなのか言われてもピンと来ないのに対して、比であれば「長さは関係なく形に注目」させることができるのでテレビサイズの説明に適しているというわけです。
このように、ざっくりとしたイメージを伝えるのに比は便利なのです。
比の使い方
最後に比の使い方について説明します。比はあくまで比率(分数)なのでそれ自体で具体的な長さや量を表しているわけではありません。料理の例でいえば、1/2カップと比で表したところで具体的に何mlを用意すればよいのかは分かりません。なので、比から具体的な長さや量は計算で求める必要があります。
具体的な数量の計算公式
ではどのように計算すれが良いのかですが、意外と簡単に計算できます。
■具体的な数量の計算方法
$$\color{red}{\textrm{求めたいもの}=\textrm{基準}\times\textrm{比(分数)}}$$
→基準量に比を掛け算すると求めたい数量が計算できる!
ざっくり公式にするとこんな感じです。言葉の意味ですが、「求めたいもの」というのは知りたい値のことです。「基準」とは、比で基準として使われている量のことで、具体例で説明したほうが分かりやすいので後で解説します。「比(分数)」は言葉の通り分数で表された比のことです。
具体的な計算例
数式にしてしまうと意外と分かりにくいかもしれませんが、例えば水を3/4カップ用意するとき何mlの水が必要かを計算してみましょう。1カップは200mlとします。
これをポイントの公式に当てはめるとこうなります。まず、「求めたいもの」は水の量です。次に「基準」ですが今回は「3/4カップ」という比が登場しているので、この比の基準となっている量、すなわち1カップである200mlという量が基準になります。最後の比は\(\small \frac{3}{4}\)ですね。
これで計算してみると、\(\small \textrm{求めたいもの}=200\textrm{ml} \times \frac{3}{4}=150\textrm{ml}\)と計算できました。水は150ml必要ということですね。
このように、基準量に比を掛け算すると求めたい数量が計算できるということをしっかり覚えておいてください。
【本題】三角比を徹底解説
お待たせしました!では、ここから本題の三角比について解説します。ここまで前提知識である比について解説したのは皆さんもお気づきの通り三角比も「比」だからです。比について理解した皆さんならこの後の解説も「なるほど!」と納得できるレベルになっていると思うので、早速解説していきます!
三角比とは?
三角比とは「直角三角形の辺の比」のことです。直角三角形の辺のうち2つを比べて分数にしたものということです。比=分数という考え方が早速出てきましたね。
直角三角形には辺が3つあるのでそこから2つの辺を比にするので、どの辺同士の比較なのかが分かるようにそれぞれ名前がついています。それが皆さんもご存じ、サイン(sine)、コサイン(cosine)、タンジェント(tangent)です。
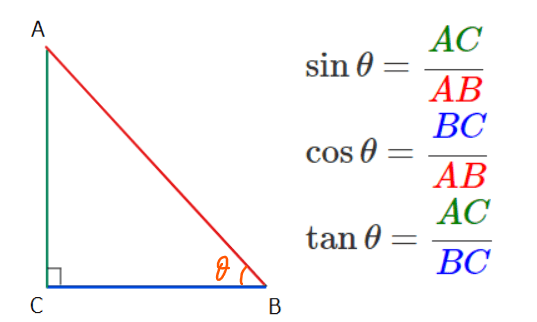
たとえば、上図で赤い辺と青い辺の比が知りたかったら、コサインの値を計算すればよいというわけです。
【豆知識】知られざる裏の三角比!?
三角比には上の3つ以外にも種類があるのをご存じでしょうか?三角比の定義を復習すると「直角三角形の辺のうち2つを比べて分数にしたもの」でした。2つの辺の比べ方って他にもありますよね?それが以下の3パターンです。
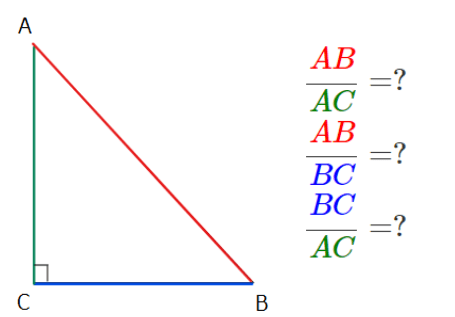
つまり、サインやコサインなどの分母と分子を逆にした比のことです。実はこのような比にもちゃんと名前がついていて、それぞれ\(\small \csc\)(コセカント)、\(\small \sec\)(セカント)、\(\small \cot\)(コタンジェント)といいます。
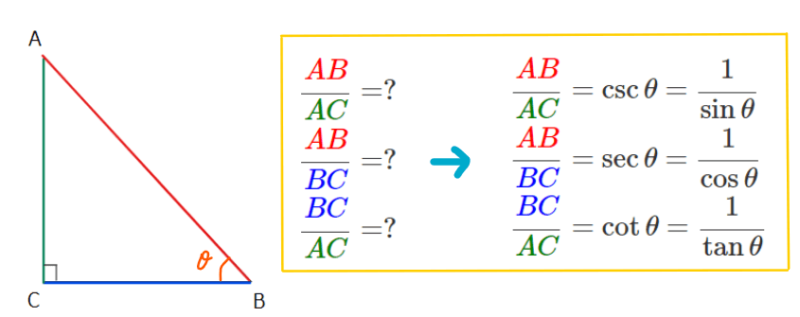
ただ、逆数ということで本質的ではないので学校ではあまり触れられませんが、こんな三角比もあるというのは知っておいてもよいかもしれません。
なぜ直角三角形なのか?
ここで三角比が辺の比だということは分かったけど、なんで直角三角形?という疑問が出てきます。確かに三角形の辺の比を考えるだけなら、正三角形や二等辺三角形、なんならただの鋭角三角形でもよさそうです。
その中であえて直角三角形が選ばれるのには理由があります。その理由はズバリ「辺の比と角度の関係性がちょうどいい感じだから」です。
どういうことかというと、例えば正三角形で三角比を考えたとします。そうすると正三角形は必ず角度が60°ですから、\(\small \sin 60°,\cos 60°,\tan 60°\)のような3パターンしか生まれません。また、辺の長さも3辺とも同じ長さですからどこの辺との比をとっても絶対に1です。これではあえて三角比のような定義を作っても意味がありませんね…。
逆に、何の変哲もない鋭角三角形を考えたとしましょう。すると辺の長さは三角形によっていろいろなバリエーションがあるので、辺の比を考えること自体は意味がありそうです。ただ、三角比では\(\small \sin〇°\)のように角度で辺の比を定義しないといけません。一般的な三角形だと例えば、角度が30°の三角形を\(\small \sin 30°\)と定義しようとしてもいろんな三角形が描けてしまい一つに定まりません。よって辺の比も1つに定まらず、これでは三角比を定義できないんです(下図参照)。
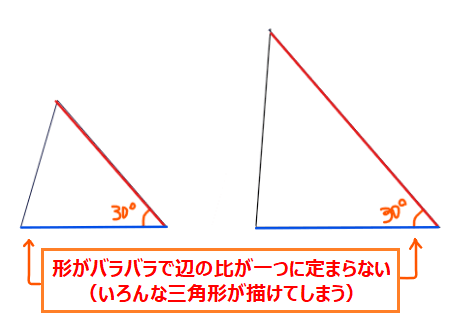
例えば赤い辺と青い辺の比を求めると右側の三角形と左側の三角形で
値が異なってしまう。よって、sin30°のような三角比を一意に定義できない。
つまり、三角比を定義するうえで重要なのは三角形の形選びということです。そして角度が決まると辺の比が決まるようなちょうどいい関係性の三角形が「直角三角形」だったということです。
三角比が重要な理由
直角三角形の辺の比を表したものが三角比だということを説明しましたが、そもそもなんで三角比を考えることが重要なのでしょうか?答えは、三角比は角度で値が決まるからです。つまり、\(\small \sin30°\)と言われればどんな直角三角形を描いたとしても辺の比は0.5で同じになるということ。具体的に斜辺が何センチで…と計って求める必要がないんです。逆に言えば、三角比が分かれば角度が分かるということです。すごいですよね…。
これは比のメリットでもお伝えした通り、具体的な長さではなくざっくりイメージを伝えられるという比のメリットを利用して三角形の辺の長さを図らなくても角度さえ分かれば辺の比が分かってしまうということです。
これが三角比が重要な理由です。
日常生活における三角比の使用例
最後に三角比が私たちの身の回りでどんなところに使われているのか2つほど例に挙げて解説します。
【使用例1】測量
測量とは、ものの高さなどを図る仕事で、よく道端で見かけるこんな機械を使ってお仕事している人を見たことあると思います。

測量では機械で物の長さや高さを図ることができるのですが、その際に三角比が使われています。どんなふうに使われているのかイメージを簡単に伝えると、下図のように測量するものとの距離と角度を機械が認識してそこから三角比を使って物の高さが計算されるという感じです。
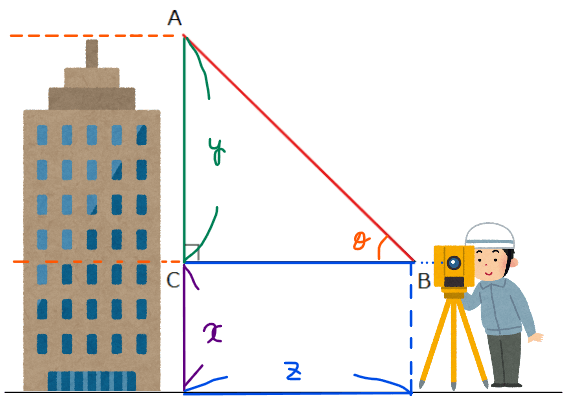
計算方法としては、測量者とビルとの距離(z)と測量計からビルの頂上までの角度(θ)および測量計の高さ(x)の情報から三角比tanθを使ってy=z tanθを計算すれば、x+yでビルの高さが計算できます。
【使用例2】線路の傾斜設計
2つ目は、線路のカーブが傾斜しているのを見たことがあると思いますがあの角度を決めるときに三角比が使われています。電車がカーブを曲がるときには遠心力が働きます。そのためカーブする際にあまりスピードが速いと外側に膨れてしまい脱線してしまうため、一定のスピードを保ちつつ走行できるようにあらかじめ線路を傾斜させておくと脱線せずかつスピードも落とさずに曲がることができます。その時にどの程度傾斜させておくべきか設計するときに三角比を使うわけです。
詳細は物理の話になるので雰囲気だけ説明すると、電車が傾斜した線路を走るときには、下図のように重力と遠心力が働きます。
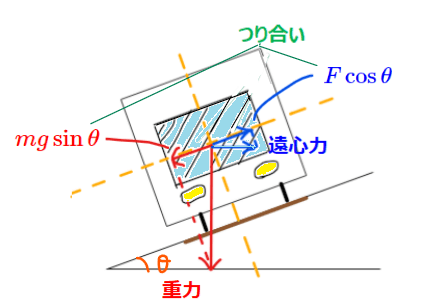
これらの力が線路と水平な方向で釣り合っていれば電車はバランスを保ったまま走行することができるので、釣り合うために必要な傾斜角\(\small \theta\)は、電車の質量を\(\small m\)、重力加速度を\(\small g\)、遠心力を\(\small F\)とすると、
$$ \color{red}{mg\sin \theta} = \color{blue}{F \cos \theta}$$
すなわち
$$\tan \theta =\frac{F}{mg}$$
を解くことで計算できます。
このように三角比は三角形の範囲を超えていろいろな場面で応用されているのです。
まとめ
今回は三角比とは何かという根本の話から、具体的にどんな場面で使用されているのかについて解説しました。学校などの授業ではいきなり三角比の定義から覚えさせられることが多く、そもそもどういうう経緯で考えられた概念なのかやどんな場面で利用されるのかがあまり説明されないので混乱してしまいますが、この記事を読んだ皆さんが、少しでも三角比のイメージを持つことができてくれたらうれしいです。
では、本日はここまでです。お疲れさまでした!




コメント