今回は、文字を含む3次関数の最大・最小を求める問題について、場合分けのコツを分かりやすく解説していきます。
- 文字が出てくるとどう場合分けすればいいのか分からなくなる…
- 場合分けの考え方のコツが知りたい!
- 最大、最小となる場所の見つけ方が知りたい!
【基礎講義】文字を含む3次関数の最大最小の求め方
文字を含む3次関数の最大最小を求めるためには、以下の3ステップで考えることがコツです。
■文字を含む3次関数の最大最小の求め方
・STEP1:問題文から描ける範囲でグラフを描く
・STEP2:定義域とグラフの位置関係に着目して場合分け
・STEP3:場合分けした条件ごとに最大値、最小値を求める
それぞれどういうことか確認していきましょう。
問題文を可視化しよう
3次関数の問題に限らず文字が含まれる問題でまず初めにやることは、イメージすることです。
イメージするうえで効果的なのがグラフを描くことです。
そもそも文字が含まれる問題が難しく感じる一番の原因は、イメージがしにくくなるからです。例えば、日本から韓国まで飛行機で何時間かかるか知りたいなと思った時に、次のAとBのどちらの解答が分かりやすいでしょうか?
●どっちが分かりやすい?
A:2時間
B:\(\small \displaystyle \frac{d}{v}\)時間 (距離:\(\small d\) km、速さ:\(\small v\)km/時)
おそらく多くの人は、「A」の方が分かりやすかったと思います。これは、「B」の解答は文字が含まれており、私たちが日常慣れ親しんでいる具体的な数字としてイメージできないからです。
文字を含む3次関数の問題もこれと同じで、文字が含まれているとグラフの概形がイメージできずに、問題の難易度が一気に上がります。なので、まずはできる範囲でグラフを描いて状況をイメージすることから始めてみましょう!
定義域とグラフの位置関係をチェック
次にやることは、定義域とグラフの位置関係に着目した場合分けです。これだけだとちょっとわかりにくいと思うので説明します。
3次関数の場合、最大値と最小値をとる場所は、\(\small x\)軸方向の範囲(=定義域)で決まります。なので、最大値/最小値を考えるには、\(\small x\)軸の範囲とグラフの位置関係をしっかり把握することが大切になります。定義域とグラフの位置関係によって最大値と最小値の位置が変わるので、そこがまさしく場合分けの境目になります。

●適切な場合分けが大事
場合分けが苦手な人は「状況が決まるように場合分けする」ことを意識しましょう。
例えば、「小学校で習う漢字」は、1年生~6年生までの6パターンに場合分けできます。「1年生で習う漢字」、「2年生で習う漢字」、…と場合分けすると、それぞれの場合で具体的に習う漢字が決まります。一方で「4月に習う漢字」など場合分けの仕方を間違ってしまうと、具体的にどんな漢字を習うのかイメージを持つことができず、答えもよく分からなくなってしまいます…(月ごとに習う漢字が決まっているわけではないので、そもそも月ごとに場合分けするのが微妙ということ)。
このように、場合分けするときは、具体的な状況が決まるように場合分けすることがポイントになります。3次関数の最大最小の場合は、定義域とグラフの位置関係で場合分けするとうまくいくというわけです。
パターンごとに最大最小を求める
場合分けさえできれば、あとはパターンごとに最大値と最小値を求めるだけです。場合分けするとグラフと定義域の位置関係が決まるので、しっかりグラフを描いて、一番高い場所を最大値、一番低い場所を最小値としてあげればOKです。
【問題&解説】文字を含む3次関数の最大最小
\(\small k>0\)とする。関数\(\small f(x)=3x^3-k^2x+1\)(\(\small 0≦x≦1\))について、次の問いに答えよ。
(1)最小値を求めよ。
(2)最大値を求めよ。
基礎講義のポイントで述べた3STEPに沿って考えていこう。
まずはグラフを描くために、関数\(\small f(x)\)を微分して極値を求める。
\begin{equation}
\begin{split}
f'(x)=&9x^2-k^2=0\\
&9x^2=k^2\\
&x^2=\dfrac{k^2}{9}\\
&\color{red}{x=\pm \dfrac{k}{3}}
\end{split}
\end{equation}
増減表は以下の通り(3次関数の場合は、\(\small x^3\)の係数でグラフの概形が決まるので\(\small f'(x)\)の符号の確認は割愛)。
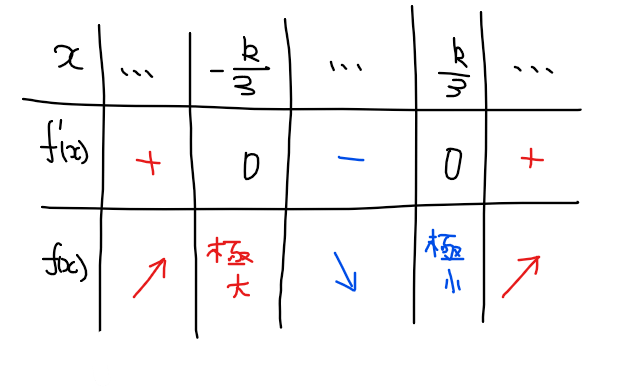
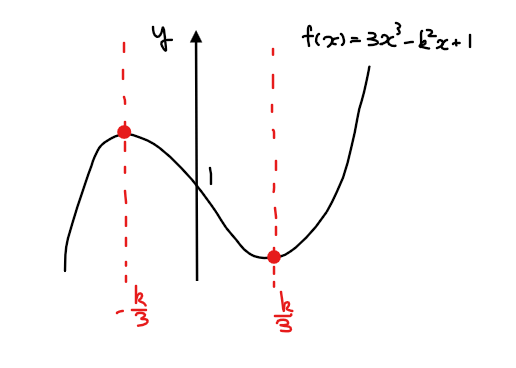
グラフは増減表から山と谷が決まるのと、切片も1であることは確定しているのでその情報を記載する。一方で、定義域\(\small 0≦x≦1\)とグラフの位置関係は確定してないので、場合分けして考える。
今回は最小値を考えればよいので、定義域に極小値が含まれるか否かが重要なポイントになる。今回は定義域の左端(\(\small x=0\))が\(\small y\)軸なので、定義域の右端(\(\small x=1\))の位置に着目する。自分でいくつかグラフと定義域の位置関係を考えてみると場合分けの境目を見つけることができるだろう。
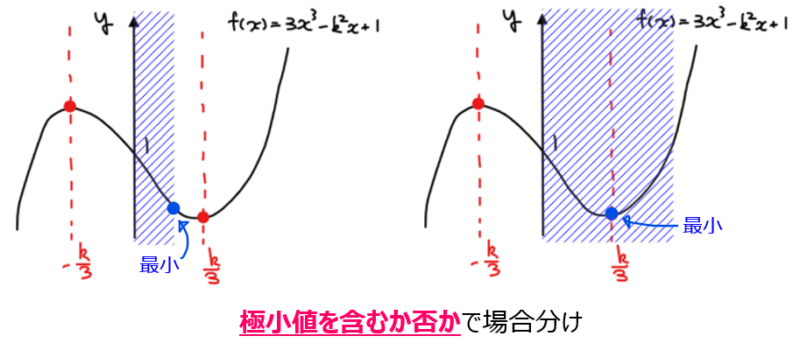
(補足)グラフはポイントをおさえていれば厳密じゃなくてOK
グラフの概形を描くときに、縮尺などをものすごく厳密に書こうとする人がいます。厳密に書くこと自体は大事なのですが、実際には試験時間は限られてますので、問題を解くために必要な最低限のポイントだけ押さえていればあとはある程度厳密じゃなくても大丈夫です。
今回の例では、定義域は\(\small 0≦x≦1\)で固定(変わらない)なので厳密には上図の青色範囲は同じ幅でグラフの概形が変わることになります。ただ、最大最小の問題を考える上ではグラフと定義域の位置関係のイメージ図を描けることが重要なのでこのような図でもよいわけです。
最小値をとる場所は、定義域内に極小値を含むか否かで決まることが分かるので、定義域の右端である\(\small x=\color{red}1\)と極小値をとるときの\(\small x\)の値である\(\small \displaystyle \color{red}{\frac{k}{3}}\)の大小関係で場合分けすればよい。
[1] \(\small \displaystyle 1≦\frac{k}{3}\)、すなわち、\(\small 3≦k\)の場合
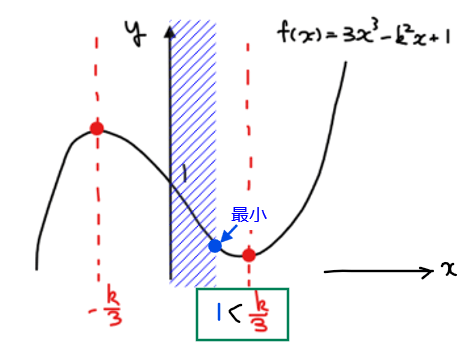
この場合、定義域右端の\(\small x\)座標である1と極小値をとるときの
\(\small \frac{k}{3}\)は図のような大小関係になる。
この場合、上図のような位置関係になるので、青色範囲である定義域内で最小値をとる場所は\(\small x=1\)のときとなる。
よって、最小値は
\begin{equation}
\begin{split}
f(1)=3\cdot\color{blue}1^3-k^2\cdot\color{blue}1+1=\color{green}{4-k^2\quad\cdots①}
\end{split}
\end{equation}
[2] \(\small \displaystyle \frac{k}{3}<1\)、すなわち、\(\small \color{red}{0<}k<3\)の場合
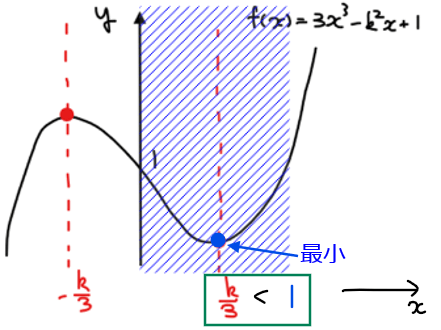
この場合、定義域右端の\(\small x\)座標である1と極小値をとるときの
\(\small \frac{k}{3}\)は図のような大小関係になる。
場合分けの条件は、単純に考えると\(\small k<3\)になるが、問題文から\(\small 0<k\)の条件があるので共通範囲をとって冒頭の条件になっていることに注意する。
この場合、図からもわかるように極小値が最小値になる。よって、\(\small \displaystyle x=\frac{k}{3}\)のときの値を求めればよいので
\begin{equation}
\begin{split}
f\left(\dfrac{k}{3}\right)=3\cdot\left(\color{red}{\dfrac{k}{3}}\right)^3-k^2\cdot\left(\color{red}{\dfrac{k}{3}}\right)+1=\color{darkorange}{1-\dfrac{2}{9}k^3 \quad\cdots②}
\end{split}
\end{equation}
(補足)極小値/極大値と最大値/最小値の違いは?
同じような用語で意外と違いがわからないまま雰囲気で使ってる人も結構いるので怪しいなと思った人は要チェック!
●最大値/最小値
考えている範囲内で一番大きい値/一番小さい値のこと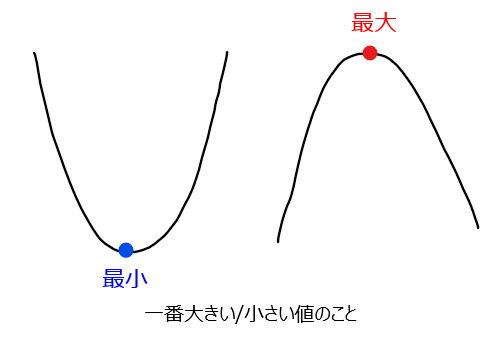
●極小値/極大値
近場だけ見たときに(局所的に)大きい/小さい値のこと
よって、①、②をまとめたものが答え。
(解答)
\(\small 0<k<3\)のとき、\(\small \displaystyle 1-\frac{2}{9}k^3 \)
\(\small 3≦k\)のとき、\(\small 4-k^2\)
最大値についても考え方は同じなので定義域とグラフの位置関係で場合分けする。

上図のようにいくつかパターンをかいてみると分かるが、定義域(青色範囲)の中にグラフがあまり入り込んでいないうちは\(\small x=0\)(\(\small y\) 軸)で最大値1をとる【場合分け①】が、グラフ右側の増加部分が入り込んでくるとある時点から定義域の右端(\(\small x=1\))で最大値をとる【場合分け②】ようになることが分かる。
この最大値が逆転する境目は、下図のように定義域右端\(\small x=1\)の時の\(\small y\)の値が\(\small y\)軸切片の1より大きくなるか否かで決まる。
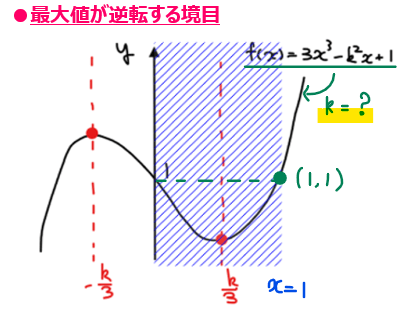
不等式で表すと
\begin{equation}
\begin{split}
\color{red}{f(1)}>\color{blue}1\\
\end{split}
\end{equation}
となる。左辺の\(\small f(1)\)(\(\small x=1\)の時の\(\small y\)の値)が右辺の1(\(\small y\)軸の切片)よりも大きくなること。
この不等式を計算すると、
\begin{equation}
\begin{split}
f(1)=3\cdot 1^3-k^2\cdot 1+1&>1\\
3-k^2+1 & >1\\
k^2 & <3\\
\Rightarrow \quad 0<k &<\sqrt{3} (\color{red}{k>0\mathrm{のため}})
\end{split}
\end{equation}
よって、\(\small 0<k <\sqrt{3}\)の場合は、\(\small x=1\)の方が\(\small y\)座標の値が大きくなるので最大値をとり、\(\small \sqrt{3}≦k\)のときは、\(\small x=0\)で最大値をとるということ。
[1] \(\small \sqrt{3}≦k\)の場合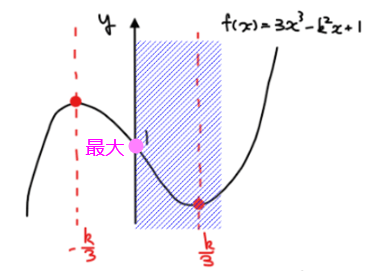
上図の通り最大値は1…①となる。
[2] \(\small 0<k<\sqrt{3}\)、の場合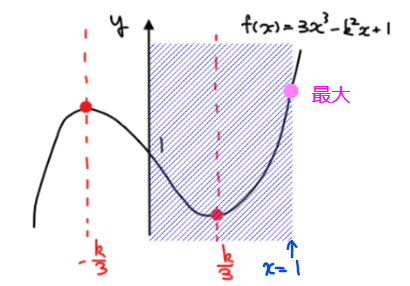
上図の通り、\(\small x=1\)の時に最大値をとるので
\begin{split}
f(1)&=3\cdot \color{blue}1^3-k^2\cdot \color{blue}1+1\\
&=\color{darkorange}{4-k^2\quad \cdots②}\\
\end{split}
よって、①、②をまとめたものが解答となる。
(解答)
\(\small 0<k<\sqrt{3}\)のとき、\(\small 4-k^2\)
\(\small \sqrt{3}≦k\)のとき、\(\small 1\)
本記事のまとめ
今回は文字を含む3次関数の最大最小の求め方を解説しました。解き方の王道は以下の3ステップでした。
■文字を含む3次関数の最大最小の求め方
・STEP1:問題文から描ける範囲でグラフを描く
・STEP2:定義域とグラフの位置関係に着目して場合分け
・STEP3:場合分けした条件ごとに最大値、最小値を求める
文字を含む3次関数の問題では、まずはグラフを描いて状況を掴むことが重要になるので、しっかりグラフを描くようにしましょう。また、場合分けをするときには、\(\small x\)の範囲とグラフの位置関係(例:グラフの極値が定義域内に含まれるか否かなど)を意識して場合分けするとうまくいくので、ぜひいろいろな問題で試してみましょう。
では今回はここまでです。お疲れさまでした!








コメント