今回は、接線・法線の方程式の求め方について解説していきます。接線・法線の方程式を求める問題は座標平面上の図形問題(面積や軌跡を求める問題)や数Ⅲで学ぶ極限の問題など多くの問題と絡めて出題しやすいことから、大学入試で頻出の分野になっています。
一方で、「公式の意味が分からない…」、「問題パターンが多すぎて解き方が分からなくなる…」など接線・法線の方程式の問題が苦手という人も多いのではないでしょうか?
接線・法線の方程式を求める典型問題は種類が多いので、本記事ではまず初めに押さえておきたい問題として共通接線の求め方、曲線上にない点を通る接線の求め方を解説します。また、そもそもなぜ微分と接線・法線が関係するのかや公式の意味といった基本的な考え方についても踏み込んで解説していきますので、是非最後まで確認してみてください!
- 接線・法線の基礎知識(公式の意味や微分との関係性)を理解したい人
- 接線の方程式の典型問題(共通接線、曲線上にない点を通る接線)の解き方を知りたい人
- 大学入試対策、定期テスト対策がしたい人
【基礎講義】接線・法線の方程式
【講義1】接線の方程式の公式
ここでは接線の方程式の公式の意味と覚えるべきポイントについて解説する。
曲線 \(\small y=f(x)\)において、\(\small x=t\)における接線の方程式は
$$\small y= f^\prime(t)(x-t)+f(t)$$
接線の方程式の公式に関して押さえておくべきポイントは次の2点。
Point①:接点の座標が\(\small (t,f(t))\)
Point②:傾きは\(\small f^\prime(t)\) \(\small = f^\prime(\) 接点の\(\small x\)座標 \(\small )\) ☆超重要!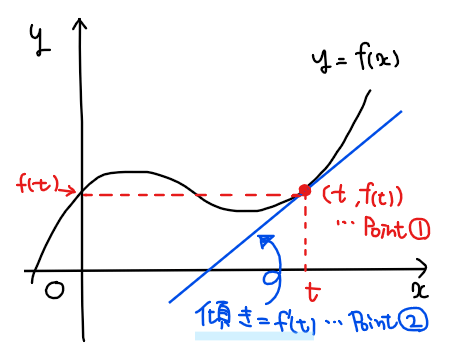
●補足
\(\small f(t)\)は\(\small x=t\)での曲線\(\small y=f(x)\)上の\(\small y\)座標のこと。
※\(\small f(t)\)って書かれるとちょっとわかりずらいですが…。
≪ここに注意!≫
よく間違えやすい点として、Point②の接線の傾き\(\small f^\prime(t)\)を求める際に代入する\(\small x\)座標の値 \(\small t\)を接線上の任意の点の\(\small x\)座標を代入すればよいと誤解・混乱している人が多い。
接線の傾きを求めるには、接点の\(\small x\)座標を代入する必要がある(上図参照)点はしっかり押さえておこう。イメージとしては、接線の傾きは曲線上のどこを接点とするかによって変わるので、接点の座標が重要になるという感覚を持っておくとよいでしょう。
どうしても混乱してしまう人は、接線の公式を
\(\small y=f^\prime(\) 接点の\(\small x\)座標 \(\small )(x-\) 接点の\(\small x\)座標 \(\small )+\) 接点の\(\small y\)座標
として覚えてしまってもOK!詳しくは問題3で確認しよう。
上記の2点を押さえていれば、直線の方程式の公式[*1]から接線の方程式は自然に導出できる。
*1:【補足】直線の方程式の公式
点\(\small (a,b)\)を通る傾き \(\small m\)の直線の方程式は
$$\small y=m(x-a)+b$$
接線の方程式は、上記公式で\(\small a=t, \space b=f(t)\), \(\small m=f^\prime(t)\)とすればよいので、
$$\small y=f^\prime(t)(x-t)+f(t)$$
であることが簡単に導ける。
*ちなみに…
直線の方程式の公式は、原点を通る直線\(\small y=mx\)を\(\small x\)軸方向に\(\small a\)、\(\small y\)軸方向に\(\small b\)だけ平行移動して点\(\small (a,b)\)を通るようにした方程式が\(\small \color{#ef5350}{y-b}=m\color{#5c6bc0}{(x-a)}\)となることから得られる。
【講義2】接線の傾き=微分係数の理由
微分係数は、数式としては
$$\small \displaystyle f^\prime(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h} \quad \cdots (*)$$
で定義される。この数式は極限があることで複雑になっているので一旦極限を取っ払った式
$$\small \displaystyle \frac{f(a+h)-f(a)}{h}$$
を考えてみると、これは
$$\small \displaystyle \frac{y \mathsf{の増加量}\quad}{x \mathsf{の増加量}\quad}$$
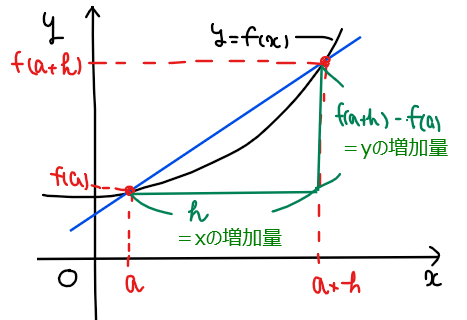
なので、区間 \(\small h\)での傾きを表している(中学数学の1次関数で習ったやつ)。
この傾きについて『区間 \(\small h \to 0\)の極限をとった傾き』=『ある点での傾き』(下図参照)となる。
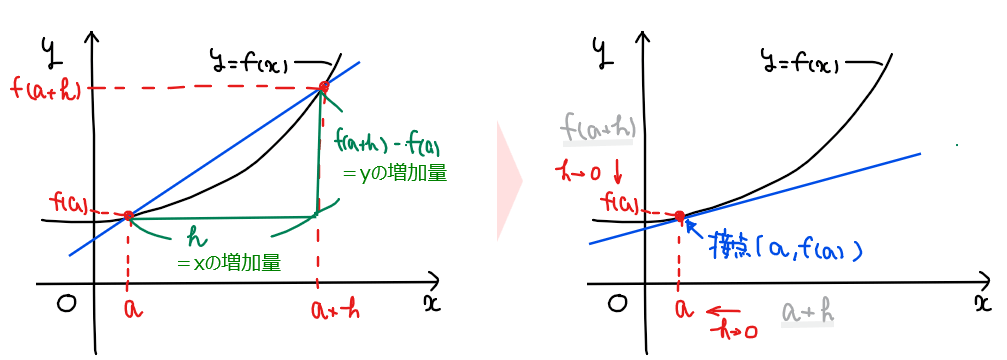
区間 \(\small h \to 0\)の極限をとった傾きが\(\small (*)\)であり、微分係数の定義そのものであることから、微分係数 \(\small f^\prime (a)\)が \(\small x=a\)での接線の傾きを表すことが分かる。
【講義3】法線の方程式の公式
法線とは、『接点において接線と垂直に交わる直線』のこと。
$$\small \displaystyle y = -\frac{1}{f^\prime (t)}(x-t)+f(t)$$
法線の方程式の公式に関しても押さえておくべきポイントは次の2点。
Point①:接点の座標が\(\small (t,f(t))\)
Point②:傾きは\(\small \displaystyle -\frac{1}{f^\prime(t)}\)で与えられる(=接線と垂直に交わる)
【補足】2直線が垂直に交わる条件
2直線の傾きを \(\small m, \space n\)とすると、垂直に交わる条件は
$$\small mn=-1$$
この関係を利用することで、法線の傾きは接線の傾き\(\small f^\prime(t)\)とかけ算して\(\small -1\)にならないといけないので、\(\small \displaystyle -\frac{1}{f^\prime(t)}\)と導出できる。
【問題&解説】接線・法線の方程式に関する問題
【問題1】接線の方程式を求める問題(難易度:★☆☆)
曲線 \(\small y=x^3-x^2-2x\)に接し、傾きが\(\small -1\)である直線の方程式を求めよ。
接点が与えられていない問題では、接点の \(\small x\)座標を\(\small t\)とおき、
接線の方程式の公式を利用して \(\small t\)の値を求める解法が定石。
【接線の方程式の公式】
曲線\(\small y=f(x)\)において、点\(\small (t, f(t))\)における接線の方程式は
$$\small y=f^\prime(t)(x-t)+f(t)$$
問題の曲線を\(\small f(x)=x^3-x^2-2x\)とおき、接点の座標を\(\small \mathrm{P}(t,t^3-t^2-2t)\)…①とおくと、
\begin{split}
\small f^\prime(x) =3x^2-2x-2\\
\end{split}
より、点\(\small \mathrm{P}\)における接線の傾きは、\(\small f^\prime(t)=3t^2-2t-2\)。題意より、この傾きが\(\small -1\)になればよいので
\begin{split}
&\small 3t^2-2t-2=-1\\
\small \Leftrightarrow \space &\small 3t^2-2t-1=0\\
\small \Leftrightarrow \space &\small (3t+1)(t-1)=0\\
\small ∴ \space &\small \displaystyle t=-\frac{1}{3}, \space 1\\
\end{split}
ここで、曲線 \(\small f(x)=x^3-x^2-2x\)の接点の\(\small x\)座標を\(\small t\)とおいていたことから、『\(\small t\)の解が2つある』 ⇔ 『接点が2箇所ある』ことが分かる。
●OnePoint
『接点の\(\small x\)座標が満たす方程式の解の個数』 \(\small =\) 『接点の個数』
[1] \(\small \displaystyle t=-\frac{1}{3}\)の場合
接点の座標は、①に\(\small \displaystyle t=-\frac{1}{3}\)を代入することで、\(\small \displaystyle \left(-\frac{1}{3},\frac{14}{27}\right)\)と求まることから、求める直線の方程式は点\(\small \displaystyle \left(-\frac{1}{3},\frac{14}{27}\right)\)を通る傾き\(\small -1\)の直線なので、
\begin{split}
&\small y=-\left(x+\frac{1}{3}\right)+\frac{14}{27}\\
\small ∴ \space &\small \displaystyle y=-x+\frac{5}{27}\\
\end{split}
… [ *1の公式を利用 ]
[2] \(\small t=1\)の場合
同様に、①より接点の座標は \(\small (1,-2)\)より、求める直線の方程式は点\(\small (1,-2)\)を通る傾き\(\small -1\)の直線なので、
\begin{split}
&\small y=-\left(x-1\right)-2\\
\small ∴ \space &\small y=-x-1\\
\end{split}
よって、求める直線の方程式は、\(\small \displaystyle \color{red}{y=-x+\frac{5}{27},}\) \(\small \color{red}{y=-x-1 \space \cdots 【答】}\)
【問題2】法線の方程式を求める問題(難易度:★☆☆)
曲線 \(\small y=x^3+x\)の点\(\small (1,2)\)における法線の方程式を求めよ。
接線の方程式同様に、公式自体を暗記するよりも法線の傾きの導出方法を理解して、傾きと通る点から直線の方程式
$$\small \color{#ef5350}{y=m(x-a)+b}$$
に当てはめて考えるのがよい。
\(\small f(x)=x^3+x\)とおくと、
$$\small f^\prime (x)= 3x^2+1$$
より、点\(\small (1,2)\)における法線の傾きは
\begin{split}
\small \displaystyle -\frac{1}{f^\prime(1)} &\small = -\frac{1}{4}\\
\end{split}
となることから、求める法線の方程式は、点\(\small (1,2)\)を通る傾き \(\small -1/4\)の直線となるので
\begin{split}
\small y &\small \displaystyle = -\frac{1}{4}(x-1)+2\\
\small ∴ \space &\small \color{red}{y= -\frac{1}{4}x+\frac{9}{4} \space \cdots 【答】}\\
\end{split}
【問題3】曲線上にない点を通る接線の方程式(難易度:★★☆)
点\(\small (3,4)\)から、放物線 \(\small y=-x^2+4x-3\)に引いた接線の方程式を求めよ。
(\(\small x=3\)のときの放物線上の\(\small y\)座標は、\(\small y=-3^2+4\cdot 3-3=0 \color{#ef5350}{\neq 4}\)となるため)
接線の傾きは接点が分からないと求められないので、接点の \(\small x\)座標を文字でおいて求めていくのが定石。
(参考)
与えられる点が接点の場合、多くの問題では「点\(\small (a,b)\)における接線の方程式を求めよ。」という表現になり、接点ではない場合、「点\(\small (a,b)\)から、…」という表現になる。
【補足】接線の傾きが\(\small f^\prime (3)\)ではない理由
講義1の注意点でも触れた通り、接線の傾きは
\(\small f^\prime(\) 接点の\(\small x\)座標 \(\small )\) ☆超重要!
で与えられることをまずは再確認しておく。
問題の放物線を\(\small f(x)\)とおくと、
$$\small f^\prime (x) = -2x+4.$$
求める接線の傾きを\(\small f^\prime (3)\)としてしまうと、「\(\small f^\prime(\) 接点の\(\small x\)座標 \(\small )\)」より、接点の\(\small x\)座標が\(\small x=3\)のときの接線の傾きを求めていることになるため、下図の青色の接線の傾きを求めていることになってしまう。一方で、今回求めたいのは点\(\small (3,4)\)を通る接線の方程式(赤色の直線)なので、接点は緑色の箇所にあるため接線の傾きは\(\small f^\prime (3)\)ではなく「\(\small f^\prime(\) 緑色接点の\(\small x\)座標 \(\small )\) 」としなければならない。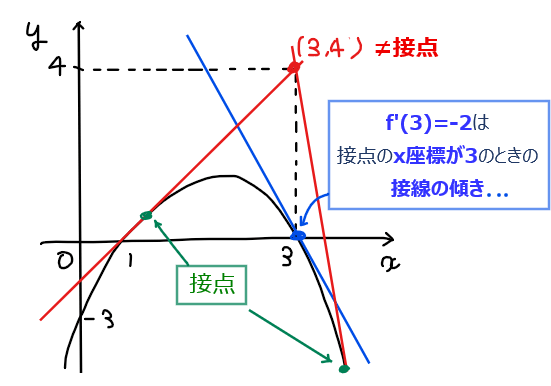
\(\small f(x)=-x^2+4x-3\)とおくと、
\begin{split}
\small f^\prime(x)=-2x+4 \space \cdots ①
\end{split}
ここで、接線の傾きを求めるためには接点の\(\small x\)座標が必要となるが、点\(\small (3,4)\)は接点ではない(放物線上の点ではない)ため、接点の\(\small x\)座標を \(\small t\)とおく。
すると①より接線の傾きは、\(\small f^\prime (t)=-2t+4\)となるので、接線の方程式は
\begin{split}
&\small y=f^\prime(t)(x-t)+f(t)\\
\small \Leftrightarrow \space &\small y=(-2t+4)(x-t)+(-t^2+4t-3)\\
\small \Leftrightarrow \space &\small y=(-2t+4)x+t^2-3 \space \cdots ②\\
\end{split}
②の接線の方程式が点\(\small (3,4)\)を通ることから、②に代入することで
\begin{split}
&\small \color{#ef5350}4=(-2t+4)\cdot \color{#ef5350}3+t^2-3\\
\small \Leftrightarrow \space &\small t^2-6t+5=0\\
\small \Leftrightarrow \space &\small (t-1)(t-5)=0\\
\small ∴ \space &\small t=1, \space 5 \quad [*1]\\
\end{split}
*1:補足
接点の\(\small x\)座標を\(\small t\)とおいていたことから、『接点が\(\small 1,5\)の2パターン』=『求める接線の方程式が2パターン』あることを意味している。
よって、求めた解を②の式にそれぞれ代入することで接線の方程式を求めることができる。
\(\small t=1\)のとき、\(\small y=2x-2 \space \cdots\)【答】、
\(\small t=5\)のとき、\(\small y=-6x+22 \space \cdots\)【答】.
【問題4】2曲線の共通接線(難易度:★★★)
2つの曲線
$$\small y=x^3+x^2-x-1, \quad y=x^2$$
の両方に接するすべての直線の方程式を求めよ。
[九州大]
・各曲線の接点の座標を文字でおき、『共通接線』 ⇔ 『接線の傾きが等しい』の関係を利用。
・『共通接線と2次関数が接する』 ⇔ 『判別式 \(\small D=0\)』の関係を利用。
*3次関数と直線の重解条件は一般的な条件がないため、2次関数と直線の重解条件を利用する
問題の曲線を
\begin{split}
&\small f(x)=x^3+x^2-x-1\\
&\small g(x)=x^2\\
\end{split}
とおく。各々の微分を計算すると
\begin{split}
&\small f^\prime (x)=3x^2+2x-1\\
&\small g^\prime (x)=2x\\
\end{split}
共通接線と曲線 \(\small y=f(x), \space y=g(x)\)との接点の座標をそれぞれ \(\small \mathrm{P}(t,t^3+t^2-t-1)\), \(\small \mathrm{Q}(s,s^2)\)とすると、点\(\small \mathrm{P}\), 点\(\small \mathrm{Q}\)における接線の傾きはそれぞれ
\begin{split}
&\small f^\prime (t)=3t^2+2t-1\\
&\small g^\prime (s)=2s\\
\end{split}
となるが、共通接線であることから
\begin{split}
&\small f^\prime (t)=g^\prime (s) \quad \mathsf{\color{magenta}{◀接線の傾きは同じ(下図参照)}}\\
\small ∴ \space &\small \color{#ef5350}{3t^2+2t-1=2s} \quad \cdots ①\\
\end{split}
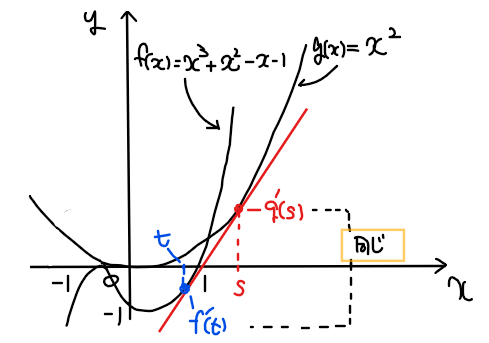
接線の傾き\(\small f^\prime (t)\), \(\small g^\prime (s)\)は等しくなる。
※なお、説明用にグラフをかいたが、
問題を解く上ではグラフをかく必要はない
が成り立つ [*1]。
*1:【補足】共通接線の傾きに関する立式について
共通接線の接点の求め方についてよくある間違いを解説する。
間違った解答
2曲線 \(\small y=f(x), \space y=g(x)\)の接線の傾きは、
\begin{split}
&\small f^\prime (x)=3x^2+2x-1\\
&\small g^\prime (x)=2x\\
\end{split}
共通接線の接線の傾きが等しいことから、
\begin{split}
&\small \color{#ef5350}{3x^2+2x-1=2x}\\
&\small \Leftrightarrow \space \displaystyle x= \pm \frac{1}{\sqrt{3}}\\
\end{split}
が接点の\(\small x\)座標である。 …これは間違い
***
では、この解答はどこに誤りがあるのか考えてみよう。
間違っているのは、『接線の傾きが等しい』=『\(\small 3x^2+2x-1=2x \)が成り立つ』としている点である。\(\small f^\prime (x)\)や\(\small g^\prime (x)\)はあくまで導関数(関数を微分した関数)であり、接線の傾きではない。接線の公式の解説でも触れているように、接線の傾きは導関数 \(\small f^\prime (x)\)に接点の \(\small x\)座標を代入した値 \(\small f^\prime (t)\)である。2曲線が共通接線と接する点は一般的には異なるため、本編の解答のようにそれぞれの接点の座標を文字でおき、\(\small f^\prime (t)=g^\prime (s)\)という立式をする必要がある。
接点 \(\small \mathrm{P}\)に着目して共通接線の方程式を \(\small t\)を用いて表す [*2]と
\begin{split}
&\small y=f^\prime (t)(x-t)+f(t)\\
\small \Leftrightarrow \space &\small y=(3t^2+2t-1)(x-t)+t^3+t^2-t-1\\
\small∴ \space &\small y=(3t^2+2t-1)x-2t^3-t^2-1\quad \cdots ②\\
\end{split}
*2:【補足】接点 \(\small \mathrm{P}\)に着目する理由
接点 \(\small \mathrm{Q}(s,s^2)\)の方がシンプルなのでこっちに着目して接線の方程式を考えるのはダメなの?と考えた人もいるだろう。仮に点 \(\small \mathrm{Q}\)に着目して論証を進めた場合、共通接線の方程式は
\begin{split}
&\small y=g^\prime (s)(x-s)+g(s)\\
&\small \Leftrightarrow \space y=2s(x-s)+s^2\\
&\small ∴ \space y=2sx-s^2\
\end{split}
と求めることができるが、今後の展望として曲線 \(\small f(x)=x^3+x^2-x-1\)と連立させて重解を持つ条件から \(\small s\)を求めていきたいので、連立させた方程式が
$$\small x^3+x^2-x-1=2sx-s^2$$
のような3次方程式になってしまうと一般的に重解を持つ条件が定まっていないことから論証が複雑化する可能性がある。そのため、点 \(\small \mathrm{P}\)に着目して、曲線 \(\small g(x)=x^2\)と連立させることで2次方程式の重解を持つ条件に帰着させる解法を選択している。
②の共通接線と曲線 \(\small g(x)=x^2\)の交点を求めるためには、お互いの方程式を連立させて
\begin{split}
&\small x^2=(3t^2+2t-1)x-2t^3-t^2-1\\
\small \Leftrightarrow \space &\small x^2-(3t^2+2t-1)x+2t^3+t^2+1=0\\
\end{split}
の2次方程式を解けば求めることができる [*3]が、今回は②の共通接線と曲線 \(\small g(x)=x^2\)が接することが条件になることから、『上記の2次方程式の解が1つ』 ⇔ 『判別式 \(\small D=0\)』より
\begin{split}
\small D = &\small (3t^2+2t-1)^2-4(2t^3+t^2+1)=0\\
\small \Leftrightarrow \space &\small 9t^4+4t^2+1\\
&\small \space +12t^3-4t-6t^2\\
&\small \space \space -8t^3-4t^2-4=0\\
\small \Leftrightarrow \space &\small 9t^4+4t^3-6t^2-4t-3=0 \space \cdots ③\\
\end{split}
*3:【補足】関数の交点と連立方程式
文字がたくさん出てくると複雑に見えるが、やっていることは単純に直線(接線はたかが直線)と放物線(\(\small y=x^2\))の交点を求めているだけ。例えば『直線 \(\small y=x+2\)と放物線 \(\small y=x^2\)の交点を求めよ』という問題があれば、\(\small x^2=x+2\) のように方程式を連立して \(\small x^2-x-2=0\)の2次方程式を解いて交点を求めるのと同じ。
あとは、上記の4次方程式を解いて\(\small t\)の値を求めることができれば、②に代入することで共通接線を求めることができる。
高次方程式は一般的な解法はないが入試問題で出題される方程式はうまく解けるようになっているので、基本的には3次方程式と同様に解を見つけて筆算や係数比較を利用してとけばよい。
③の左辺に\(\small t=1\)、\(\small t=-1\)を代入すると0になることから、因数定理より、③の左辺は\(\small (t-1)(t+1)\)を因数に持つ。このことから③の左辺は
\begin{split}
&\small 9t^4+4t^3-6t^2-4t-3=(t^2-1)(at^2+bt+c)\\
\end{split}
とおくことができる(4次式を2次式(\(\small t^2-1\))で割った商は2次式)。すると、\(\small t^4\)と定数項の係数比較より直ちに\(\small a=9, \space c=3\)が確定するので
\begin{split}
&\small (t^2-1)(9t^2+bt+3)\\
\end{split}
\(\small b\)については展開した際の\(\small t^3\)の係数が4になればよいが、展開すると\(\small t^3\)の項は\(\small bt^3\)のみなので、\(\small b=4\)に確定する。
【補足】係数比較による因数分解
高次方程式の因数分解の方法には、筆算や組立除法の利用があるが、本編では係数比較を利用した因数分解で解いている。この解法は身につければ高速で解ける裏ワザなのでぜひ習得しておきたい。詳細の解説は「【3次方程式】裏ワザあり!?因数分解、因数定理、組立除法、係数比較を用いた解法のコツ」を参照されたい。
よって、③の左辺は、
\begin{split}
&\small (t+1)(t-1)(9t^2+4t+3)\\
\end{split}
と因数分解できる。\(\small 9t^2+4t+3\)ついてはこれ以上因数分解できないので以上で因数分解は完了である。
【補足】筆算を用いた因数分解
③の左辺 \(\small 9t^4+4t^3-6t^2-4t-3\)を\(\small t^2-1\)で除算すると、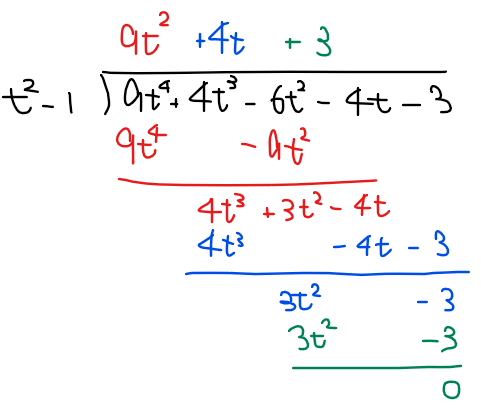
より、\(\small 9t^4+4t^3-6t^2-4t-3=(t^2-1)(9t^2+4t+3)\)と求めてもよい。
以上より、③は
\begin{split}
&\small (t+1)(t-1)(9t^2+4t+3)=0\\
\end{split}
であり、\(\small 9t^2+4t+3\)は判別式 \(\small D/4=4-27<0\)より実数解を持たないことから、上記方程式の実数解は \(\small t=\pm1\)。
よって、②の共通接線の方程式にそれぞれ代入することで、\(\small y=4x-4, \space y=0\)…【答】.
【問題5】接点における共通接線(難易度:★★☆)
2曲線 \(\small y=x^3-2x+1, \space y=x^2+2ax+1\)が接するとき、定数 \(\small a\)の値を求めよ。
また、その接点における共通の接線の方程式を求めよ。
①:2曲線の接点における接線の傾きが等しい
②:2曲線の接点の\(\small y\)座標が等しい
の2つの条件をもとに \(\small t\)の値を求めるのが定石。
2曲線を
\begin{split}
&\small f(x)=x^3-2x+1\\
&\small g(x)=x^2+2ax+1\\
\end{split}
とおく。各々の微分を計算すると
\begin{split}
&\small f^\prime (x)=3x^2-2\\
&\small g^\prime (x)=2x+2a\\
\end{split}
ここで、2曲線の接点の\(\small x\)座標を\(\small x=t\)とおくと
・2曲線の接点における接線の傾きが等しい
⇔ \(\small \color{#ef5350}{f^\prime (t)=g^\prime (t) \space \cdots ①}\)
・2曲線の接点の\(\small y\)座標が等しい
⇔ \(\small \color{#ef5350}{f(t)=g(t) \space \cdots ②}\)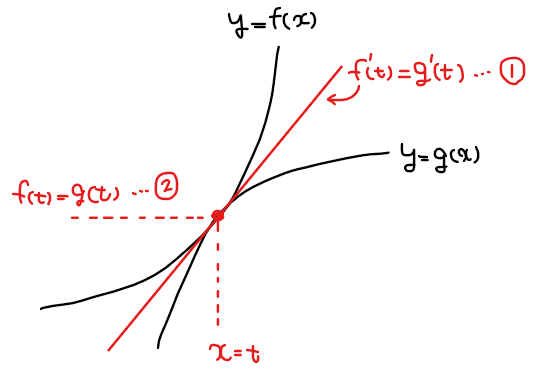
が成り立つ。
①の条件より
\begin{split}
&\small 3t^2-2=2t+2a\\
\small \Leftrightarrow \space &\small 3t^2-2t-2a-2=0 \space \cdots ③\\
\end{split}
②の条件より
\begin{split}
&\small t^3-2t+1=t^2+2at+1\\
\small \Leftrightarrow \space &\small t^3-t^2-2(a+1)t=0\\
\small \Leftrightarrow \space &\small t(t^2-t-2a-2)=0 \space \cdots ④\\
\end{split}
③、④は、2つの文字 \(\small a, \space t\)と2つの連立方程式なので文字を1つ消去することで解くことが可能である [*1]。
*1:【補足】連立方程式が解ける条件
\(\small n\)個の文字を含む方程式が最低でも\(\small n\)個あれば理論上は\(\small n\)個の文字を特定することができる(=\(\small n\)元連立方程式の解を求めることができる)。
③、④は\(\small t\)の2次方程式になっているので、\(\small a\)を消去する方針で考えると、ちょうど両方の式に\(\small 2a\)が共通していることから、③を
\begin{split}
&\small 2a=3t^2-2t-2 \space \cdots ⑤\\
\end{split}
と変形して④に代入することで
\begin{split}
&\small t(t^2-t-\color{#ef5350}{(3t^2-2t-2)}-2)=0\\
\small \Leftrightarrow \space &\small t(2t^2-t)=0\\
\small \Leftrightarrow \space &\small t^2(2t-1)=0\\
\small ∴ \space &\small \displaystyle t =0,\space \frac{1}{2}\\
\end{split}
求めた\(\small t\)を⑤に代入することで\(\small a\)の値は、\(\small \displaystyle a=-1, \space -\frac{9}{8}\)…【答】.
また、このときの共通接線の方程式は、\(\small t\)が接点の\(\small x\)座標であることから、それぞれ求めることができる。
[1] \(\small t=0\)の場合(\(\small a=-1\)のとき)
接点の\(\small y\)座標は\(\small f(0)=1\)(\(\small g(0)\)の値を求めてももちろんOK。どちらも同じ値になる)、接線の傾きは\(\small f^\prime (0)=-2\)(こちらも\(\small g^\prime (0)\)の値から求めても可)より、共通接線は点 \(\small (0,1)\)(=切片)を通る傾き\(\small -2\)の直線なので、\(\small y=-2x+1\)…【答】.
[2] \(\small \displaystyle t=-\frac{1}{2}\)の場合\(\small \displaystyle \left(a=-\frac{9}{8}のとき\right)\)
接点の \(\small y\)座標は\(\small \displaystyle f\left(\frac{1}{2}\right)=\frac{1}{8}\)、接線の傾きは\(\small \displaystyle f^\prime\left(\frac{1}{2}\right)=-\frac{5}{4}\)より、共通接線は点 \(\small \displaystyle \left(\frac{1}{2},\frac{1}{8}\right)\)を通る傾き\(\small \displaystyle -\frac{5}{4}\)の直線なので、
\begin{split}
&\small \displaystyle y=-\frac{5}{4}\left(x-\frac{1}{2}\right)+\frac{1}{8}\\
\small ∴ \space &\small \displaystyle \color{red}{y=-\frac{5}{4}x+\frac{3}{4} \space \cdots 【答】}\\
\end{split}
【考察】判別式の利用について
2曲線が接する条件として、「2曲線の接点における接線の傾きが等しいこと」と「接点での \(\small y\)座標が等しいこと」の2つの条件から求めていったが、2つ目の条件は問題4のように「放物線 \(\small y=x^2+2ax+1\)と接線が重解を持つ ⇔ 判別式 \(\small D=0\)」という条件で考えるのはダメなのだろうか?
結論、条件式としては間違っていないが、1つ目の条件である2曲線の接線の傾きが等しいことという条件と情報量が変わらないため連立しても\(\small t, a\)の値を求めることはできない。
このことは少し考えてみると分かるのだが、2曲線の接点における接線の傾きが等しい時点で、放物線と接線が接するという条件は必ず満たされる(逆に言えば2曲線の接点における接線の傾きが等しいのに放物線と接しない状態を図示できない)ということだ。そのため2つ目の条件である接点における\(\small y\)座標が等しいという条件が必要となる。
本記事のまとめ
今回は接線・法線の方程式の求め方と典型問題として曲線上にない点を通る接線を求める問題、共通接線を求める問題について解説しました。接線の問題としてはまず初めに押さえておきたい問題なので、解き方と考え方含めてしっかり復習しておきましょう。
最後に本記事のポイントを復習して終わりにしましょう。
☆重要Point☆
・曲線 \(\small y = f(x)\)における接線の傾きは、
接点の\(\small x\)座標を\(\small x=t\)としたときに\(\small f^\prime (t)\)で与えられる。
⇒(接線の傾き) \(\small =f^\prime(\) 接点の\(\small x\)座標 \(\small )\) ☆超重要!
・曲線 \(\small y = f(x)\)における法線の傾きは、接線に直交することから\(\small \displaystyle -\frac{1}{f^\prime (t)}\)と導出できる。
・接線の方程式を求める問題では、接点の把握が重要!
*接点の座標が分からない場合は、接点の\(\small x\)座標を文字でおく
・共通接線を求める問題は、「2曲線の接線の傾きが等しい」ことを利用する。
今回は以上です。お疲れさまでした!








コメント