今回は3次関数の接線の本数を求める問題について、解き方と考え方を徹底解説していきます。
問題自体はシンプルですが考え方が複雑で何を求めているのかを丁寧に追っていかないとすぐに分からなくなってしまう分野なので、苦手な人は当たり前と思っている部分も含めてしっかり理解できているか一つ一つ確認していきましょう!
- 3次関数の接線の本数を求める問題の解き方を理解したい人
- 方程式の解の個数が接線の本数になる考え方を理解したい人
- 大学入試対策、定期テスト対策がしたい人
【問題&解説】3次関数の接線の本数
【問題1】3次関数の接線の本数(定数分離の利用)(難易度:★★☆)
\(\small a\)を定数とする。3次関数 \(\small y=x^3+3x^2+x\)に点\(\small \mathrm{A}(1,a)\)から引ける接線の本数を求めよ。
※\(\small t\)は接点の\(\small x\)座標
→定数分離することで定数関数と\(\small t\)の関数の交点の個数をグラフから求める問題に帰着できる。
・3次関数の場合は『\(\small t\)の方程式の解の個数』=『接点の個数』=『接線の本数』が成り立つ(詳細は解説を参照)。
\(\small f(x)=x^3+3x^2+x\)とおき、3次関数\(\small f(x)\)との接点の\(\small x\)座標を\(\small t\)とおく[*1]。
*1:【補足】「点…における接線」、「点…から引ける接線」の違い
上記の2つは表現が似ているが意味が全く異なるので要注意。
「点\(\small (a,b)\)における接線」であれば点\(\small (a,b)\)は接点になる。一方で、「点\(\small (a,b)\)から引ける接線」であれば点\(\small (a,b)\)は基本的には曲線上にない点(接点ではない)を指す。
接線の傾きを求めるために関数 \(\small f(x)\)を微分すると
\begin{split}
\small f^\prime(x) =3x^2+6x+1\\
\end{split}
より、接点 \(\small x=t\)における接線の傾きは
\begin{split}
\small f^\prime(t) =3t^2+6t+1\\
\end{split}
よって、求める接線の方程式は、接点 \(\small (t,f(t))\)を通る傾き \(\small 3t^2+6t+1\)の直線になることから
\begin{split}
&\small y=f^\prime (x)(x-t)+f(t)\\
\small \Leftrightarrow \space &\small y=(3t^2+6t+1)(x-t)+t^3+3t^2+t\\
\end{split}
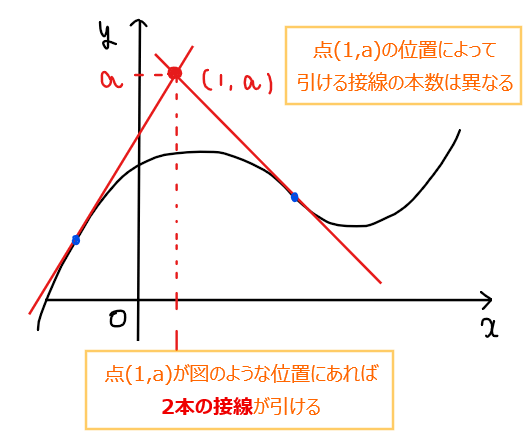
題意より、上記の直線の方程式が点 \(\small (1,a)\)を通ることから
\begin{split}
&\small \color{#ef5350}a=(3t^2+6t+1)(\color{#ef5350}1-t)+t^3+3t^2+t\\
\small \Leftrightarrow \space &\small a=-2t^3+6t+1 \space \cdots (*)\\
\end{split}
ここで\(\small (*)\)は\(\small t\)に関する3次方程式なので、\(\small (*)\)の方程式の解が求まるということは接点の\(\small x\)座標が求まることと同義である(そもそも\(\small t\)は3次関数\(\small f(x)\)との接点の\(\small x\)座標であるため)。
さらに、\(\small (*)\)の解が \(\small t =\alpha ,\beta ,\gamma\)のように求まったとすると、これは接点の\(\small x\)座標が、\(\small \alpha, \beta, \gamma\)の3か所あることを意味するので、解の個数が接点の個数に相当することが分かる(3次方程式の解は一般的には3個だが、重解などにより2個や1個の場合もある)。そして、3次関数の場合は1つの接点に対して接線は1本のみ (詳細は「【講義1】解の個数と接線の本数の関係性」で解説)であることから、『接点の個数 \(\small =\) 接線の本数』に対応する。
以上のことをまとめると、\(\small (*)\)の3次方程式の解の個数が接線の本数と考えることができる。あとは\(\small (*)\)の解の個数が分かればよいのだが、3次方程式の解の個数は2次方程式でいう判別式よりも判定条件が複雑で求めるのが大変(判定条件は【応用編】極値条件の利用で解説)なので、少しでも楽な方法がないかを考える。
そこで問題解決のKeyでも触れた通り、\(\small (*)\)を3次方程式とみなすのではなく、左辺の定数関数 \(\small y=a\)と右辺の3次関数 \(\small y=-2t^3+6t+1\)の交点を求める方程式と捉え直してみよう [*2]。
*2:【補足】関数の交点と方程式
方程式の解の個数を2つの関数の交点の個数の問題に置き換えて解くという考え方は、2次関数以外で解の個数を求める問題でよく利用される考え方なのでこの機会にしっかり理解しておこう。詳細は「【講義2】グラフを用いた接線の本数の求め方2選」の解説を参照。
本問はこの考え方を利用すると、右辺の3次関数 \(\small y=-2t^3+6t+1 \)と左辺の定数関数 \(\small y=a\)の交点を求める方程式と解釈できる。この方程式を解くことで出てきた解の個数が関数の交点の個数になることから、両者のグラフの概形を図示して交点の個数を数え上げることで解の個数が求まり、接線の本数を求めることができる。
定数関数 \(\small y=a\)と3次関数 \(\small y=-2t^3+6t+1\)の交点の個数を調べるために、両者のグラフの概形を考える。定数関数 \(\small y=a\)は\(\small a\)の値によって位置は上下するものの横一直線の関数であることは直ぐにわかるので、あとは3次関数 \(\small y=-2t^3+6t+1\)の概形が分かればよい。
関数の増減を調べるために3次関数を微分すると
\begin{split}
&\small y^\prime =-6t^2+6\\
\small \Leftrightarrow \space &\small y^\prime =-6(t^2-1)\\
\end{split}
より、\(\small y^\prime >0\)となるのは
\begin{split}
\small -6 &\small (t^2-1)>0\\
\small \Leftrightarrow \space &\small t^2-1<0\\
\small \Leftrightarrow \space &\small (t-1)(t+1)<0\\
\small ∴ \space &\small \color{#ef5350}{-1<t<1}\\
\end{split}
逆に\(\small y^\prime <0\)となるのは、\(\small t<-1, \space 1<t\)。
よって、増減表とグラフの概形は下図のようになる。
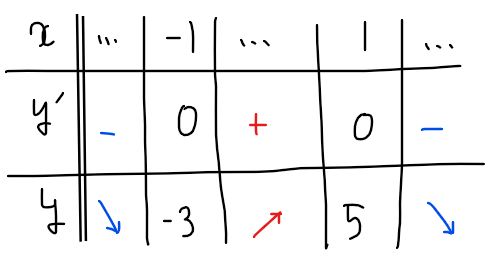
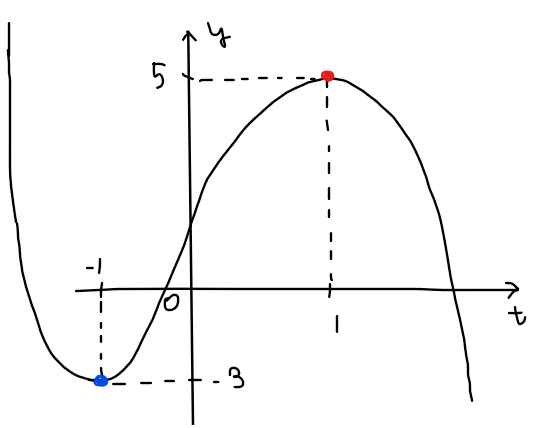
概形が図示できたので、あとは定数関数 \(\small y=a\)(横一直線の関数)の位置関係に応じて交点の個数(解の個数)が何個になるかを確認すればよい。
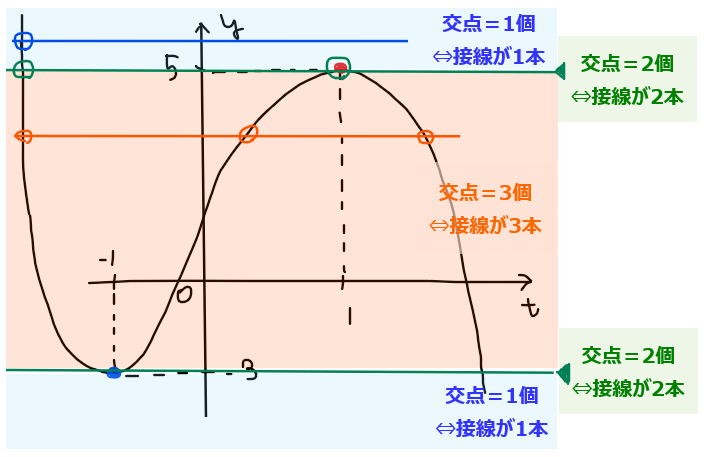
●補足
定数関数と3次関数の交点の個数を調べるときは、横線を引いて3次関数と交わる点が何個あるかを数えればよい。
上図のように\(\small a\)の値を上下させて3次関数との交点の個数を調べてみると、
・\(\small a<-3, \space 5<a\)のとき交点は1個
・\(\small a=-3, \space 5\)のとき交点は2個
・\(\small -3<a<5\)のとき交点は3個
であることが分かる。
よって、
\(\small a<-3, \space 5<a\)のとき接線は1本、
\(\small a=-3, \space 5\)のとき接線は2本、
\(\small -3<a<5\)のとき接線は3本 …【答】
【問題2】3次関数の接線の本数(極値条件の利用)(難易度:★★★)
点\(\small (a,b)\)を通り曲線\(\small C:\) \(\small y=x^3-x\)に接する接線が2本引けるとき、\(\small a,b\)が満たす関係式を求めよ。ただし、\(\small a>0\)、\(\small b \neq a^3-a\)とする。
曲線\(\small C\)を\(\small f(x)=x^3-x\)、接点の\(\small x\)座標を\(\small t\)とおく。接線の傾きは、
$$\small f^\prime (t) =3t^2-1$$
なので、接線の方程式は、
\begin{split}
&\small y=f^\prime (t)(x-t)+f(t)\\
\small \Leftrightarrow \space &\small y=(3t^2-1)(x-t)+t^3-t\\
\small \Leftrightarrow \space &\small y=(3t^2-1)x-2t^3\\
\end{split}
この接線が点 \(\small (a,b)\)を通ることから、
\begin{split}
&\small b=(3t^2-1)a-2t^3\\
\small \Leftrightarrow \space &\small 2t^3-3at^2+a+b=0 \space \cdots ①\\
\end{split}
①は接点の\(\small x\)座標 \(\small t\)に関する3次方程式であることから、①の方程式の解の個数 \(\small =\) 接線の本数になる。
①は定数\(\small a,b\)をきれいに定数分離できない(定数を等式の片側に分離できない)ことから、①の3次方程式が2つの実数解を持つ条件を極値の条件に着目して判別する [*1]。
*1:【補足】なんでグラフで考えるの?
①の3次方程式が2つの実数解を持つ条件を真面目に方程式的に考えようとすると、①が \(\small 2(t-\alpha)^2(t-\beta)=0\)の形に因数分解できる必要があることから展開した式を係数比較して\(\small \alpha ,\beta\)を求めて…、と泥沼にはまる。具体的な解を求める必要がない(個数だけでOK)場合は方程式的に考えるのではなく、グラフの問題に置き換えて軸との交点の個数を調べる方針が非常に簡単!
①の左辺を
$$\small g(t)=2t^3-3at^2+a+b \space \cdots ②$$
とおくと、3次方程式が2つの実数解を持つことは3次関数 \(\small g(t)\)が\(\small t\)軸と2箇所で交わることと同義である。
よって、3次関数 \(\small g(t)\)が \(\small t\)軸と2箇所で交わる条件はグラフ的な考察より、『\(\small g(t)\)が2つの極値を持つ』かつ『極値の片方が0』である。
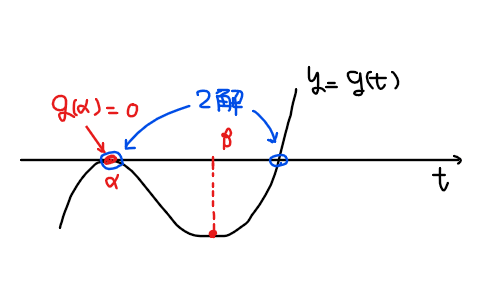
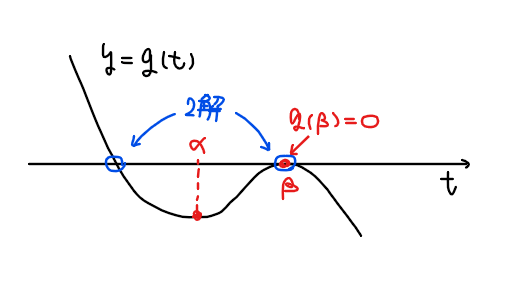
[1] \(\small g(t)\)が2つの極値を持つ
\(\small g(t)\)の極値を求める方程式は、
\begin{split}
&\small g^\prime (t)=0\\
\small \Leftrightarrow \space &\small 6t^2-6at=0\\
\small \Leftrightarrow \space &\small 6t(t-a)=0\\
\small ∴ \space &\small t=0,a\\
\end{split}
問題の条件から \(\small a>0\)なので、関数\(\small g(t)\)は常に2つの極値を持つ。
[2] 極値の片方が0
[1]で極値をとるときの\(\small t\)の値が\(\small 0,a\)であることが分かったので、それぞれの極値は、②に代入することで
\begin{cases}
\small g(0)=a+b\\
\small g(a)=-a^3+a+b\\
\end{cases}
これらのうち片方が0であればよいので、『\(\small a+b=0\) または \(\small -a^3+a+b=0\)』の条件を満たせばよい。ここで問題文中の条件 \(\small b \neq a^3-a\)より \(\small -a^3+a+b \neq 0\)であることに注意すると、後者の等式は0にならないので\(\small a+b=0\)が確定する。
【参考】
講義2の「【応用編】極値条件の利用」で解説した条件 \(\small g(0)g(a)=0\)を利用して
$$\small (a+b)(-a^3+a+b)=0$$
を数式的に解いてもよい。
以上[1],[2]の結果より、\(\small a,b\)が満たす関係式は \(\small a+b=0\)…【答】.
【考察】極値条件を利用した問題1の別解
極値条件は3次関数の実数解の個数を判別する際に一般的に使える考え方なので、もちろん問題1でも利用可能。ここでは考え方の参考として問題1を極値条件で解く方法の概略を紹介する。
ただし、実際に問題を解く際は定数分離の方が速いので、定数分離できる場合は定数分離で解き、できない場合は極値条件を利用する判断基準でOK。
(略解)
方程式 \(\small (*)\)より
$$\small 2t^3-6t+a-1=0$$
なので、\(\small g(t)=2t^3-6t+a-1\)とおくと、\(\small t\)の3次方程式の解の個数を求めたければ、関数 \(\small g(t)\)と\(\small t\)軸の交点の個数を求めればよい。
まず、関数 \(\small g(t)\)の極値を求めると
\begin{split}
&\small g^\prime (t)=0\\
\small \Leftrightarrow \space &\small 6t^2-6=0\\
\small ∴ \space &\small t=\pm 1\\
\end{split}
より、2つの極値を持ちその値は
\begin{cases}
\small g(-1)=a+3\\
\small g(1)=a-5\\
\end{cases}
となるので、
・実数解を3つ持つ条件は、\(\small g(-1)g(1)<0 \space \Leftrightarrow \space (a+3)(a-5)<0\)
・実数解を2つ持つ条件は、\(\small g(-1)g(1)=0 \space \Leftrightarrow \space (a+3)(a-5)=0\)
・実数解を1つ持つ条件は、\(\small g(-1)g(1)>0 \space \Leftrightarrow \space (a+3)(a-5)>0\)
をそれぞれ解くことで答えを求めることができる。
【基礎講義】接線の本数に関する問題で重要となる思考法
【講義1】解の個数と接線の本数の関係性
接線の本数を求める問題では、3次関数の場合、接点の\(\small x\)座標 \(\small t\)を含んだ方程式の解の個数が接線の本数であることが当たり前のように参考書に書かれているが、実はしっかり考えると「本当にそうなの?」と思えてしまう箇所なので、この章ではなぜ解の個数が接線の本数になるのかを解説する。
まず、一番はじめに確認しておきたいのが、『解の個数=接点の個数』は一般的に成り立つが、『接点の個数=接線の本数』は一般的には成り立たないため、『解の個数≠接線の本数』となるが一般的であるということ。冒頭の説明と真逆のことを言っているようで混乱したかもしれないが、『解の個数=接線の本数』となるのはあくまで3次関数の場合だけである。ここを勘違いしないように注意したい。
●OnePoint:解の個数≠接線の本数になるのはどんなとき?
ここでは解の個数(接点の個数)と接線の本数が異なる場合って具体的などんな状況なのかを紹介しておく。例としては、4次関数と接線が下図のように接する場合、接点は2個あるが接線は1本になるので、『解の個数(接点の個数)≠接線の本数』となる。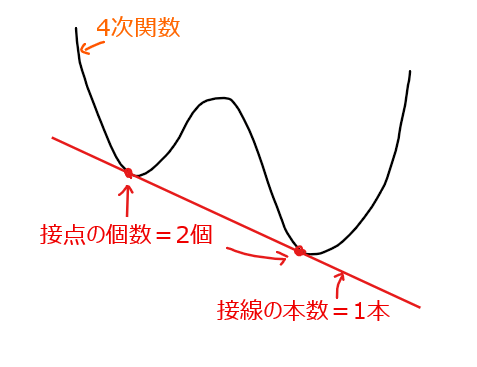
では、本題に戻って3次関数では『解の個数=接線の本数』となることを簡易的に説明する。
3次関数は3次式(\(\small y=ax^3+bx^2+cx+d\))、接線は1次式(\(\small y=mx+n\))なので交点の座標を求める方程式は
\begin{split}
&\small ax^3+bx^2+cx+d=mx+n\\
\small \Leftrightarrow \space &\small ax^3+bx^2+(c-m)x+d-n=0
\end{split}
の3次方程式を解くことで求めることができる。
3次方程式が実数解を持つときの因数分解パターンとしては、
①:\(\small (x-\alpha)(x-\beta)(x-\gamma)=0\)
②:\(\small (x-\alpha)^2(x-\beta)=0\)
③:\(\small (x-\alpha)^3=0\)
の3パターンとなるが、接点は方程式の重解であることを踏まえると該当するパターンは②または③となるので、いずれの場合も接点は\(\small x=\alpha\)の1つのみしか取り得ないことが分かる。ちなみに、②における解 \(\small x=\beta\)は接点ではなく、3次関数と接線との交点である(下図参照)。
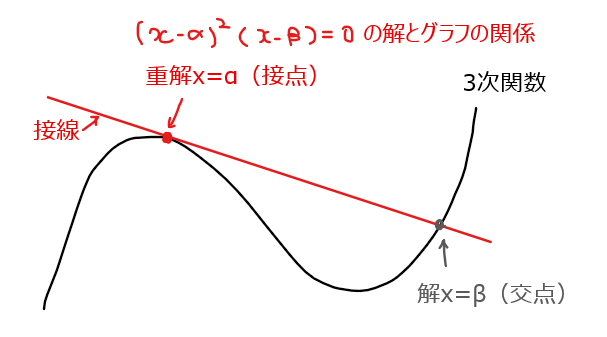
よって、3次関数では、解の個数と接線の本数が一致する。
●補足
仮に接点が2箇所ある場合、方程式が\(\small (x-\alpha)^2(x-\beta)^2=0\)のように因数分解できる必要があるため、最低限でも4次方程式になる必要があり、3次関数の場合は不可能。
【講義2】グラフを用いた接線の本数の求め方2選
【基礎編】定数分離の利用
接線の本数を求める問題の考え方として重要なのが、方程式の問題をグラフの問題に置き換えて解くという考え方である。
たとえば、放物線\(\small y=x^2\)と直線\(\small y=x-2\)の交点の座標を求めたい場合、
$$\small x^2=x-2$$
のように、2つの関数をイコールで結んだ方程式を解いていくことになる。
この考え方を逆手に利用すれば、『ある方程式の解を求める』ということは、その方程式の『左辺と右辺をそれぞれ関数とするグラフの交点を求める』ことであるとも解釈できる。関数の交点の問題はもはや方程式の問題ではなくグラフの問題になる。これが冒頭に述べた方程式の問題をグラフの問題に置き換えて解くという意味である。
では、なぜ方程式の問題をグラフの問題に置き換える必要があるのか?答えは、グラフの問題に置き換えた方が分かりやすいから(シンプル…(^^;))。
講義1でも触れたように、接線の本数\(\small =\)解の個数なので、接線の本数を求めたければ解の個数だけ分かれば十分であり、具体的な解の値(すなわち接点の座標)まではを求める必要がないということ。よって、真面目に方程式を解くのではなく関数同士の交点の個数を数える問題に置き換えて考えた方が視覚的にわかりやすいわけである。
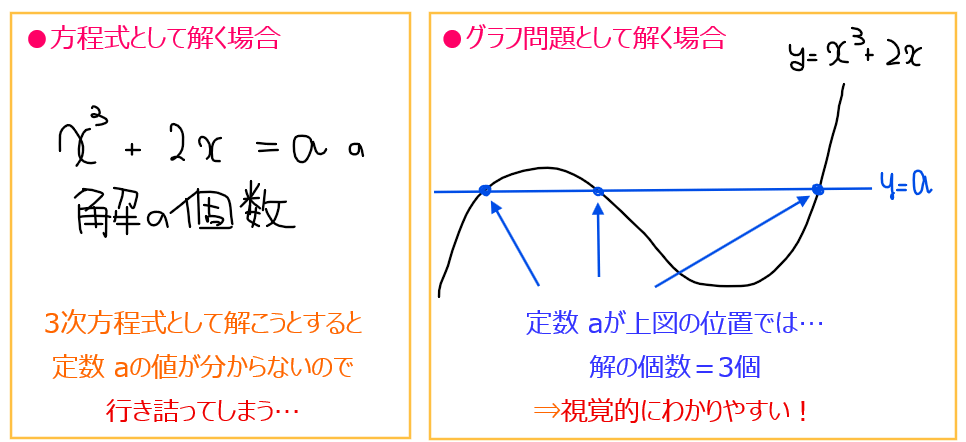
上図の右側のようなグラフ問題として解くためには、方程式の片方がシンプルな関数になっている必要がある(そうじゃないと交点がどこか結局分からなくなるため)。そこでシンプルな関数としてよく出てくるのが横一直線な関数でおなじみの定数関数 \(\small y=a\)である。
なので、解の個数を求める問題では定数分離してグラフの交点の問題として解くという思考法になるわけである。
●OnePoint
定数分離は方程式の解の個数を求める問題で頻出の考え方。実践問題に挑戦したい人は「【三角方程式】方程式の解の個数・解の存在条件の求め方」が参考になるので、併せて確認しておくとよいでしょう。
定数分離ってなに?!と思った人は以下の問題を考えてほしい。
(問題)
方程式 \(\small x^4+4x^3+1-a=0\)の解の個数を調べよ。
この問題であれば、
$$\small a=x^4+4x^3+1$$
のように『定数 \(\small a\)』と『\(\small x\)を含む関数』を左辺と右辺で分離する作業が定数分離である。
●補足
もちろん、どんな方程式でも必ず定数分離できるわけではなく、たとえば
$$\small x^3+2ax^2+3a=0$$
のような方程式の場合は、無理やり定数 \(\small a\)について解くことで
\begin{split}
&\small x^3+(2x^2+3)a=0\\
\small \Leftrightarrow \space &\small \displaystyle a=-\frac{x^3}{2x^2+3}\\
\end{split}
のように定数分離自体はできても、右辺の関数部分が複雑化してしまう。定数分離できない場合はこのあとの応用編で解説する極値条件を利用して求めることができる。
【応用編】極値条件の利用
基礎編では定数分離できる場合の解法を紹介したが、ここからは一般的に定数分離できない場合の解法について解説する。ここから解説する解き方は定数分離できる問題でも使える考え方になるが少し複雑なので、定数分離できる場合は基礎編で解説した解法で解くことをおすすめする。
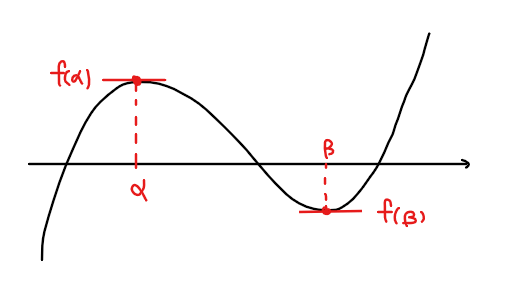
\(\small f(x)=ax^3+bx^2+cx+d\)とすると、3次方程式 \(\small f(x)=0\)の実数解の個数は3次関数 \(\small y=f(x)\)と\(\small x\)軸との交点の個数になるため、3次関数 \(\small f(x)\)の極値が満たす条件は以下のようになる。ただし、極値の\(\small x\)座標を\(\small \alpha ,\beta \space (\color{#ef5350}{\alpha < \beta})\)とする。
①3次方程式の実数解が3個 ⇔ \(\small f(\alpha)f(\beta)<0\)
*極値が異符号
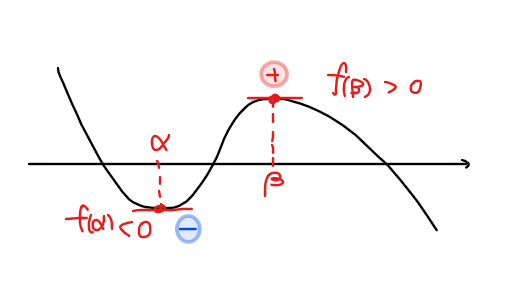
②3次方程式の実数解が2個 ⇔ \(\small f(\alpha)f(\beta)=0\)
*片方の極値が零
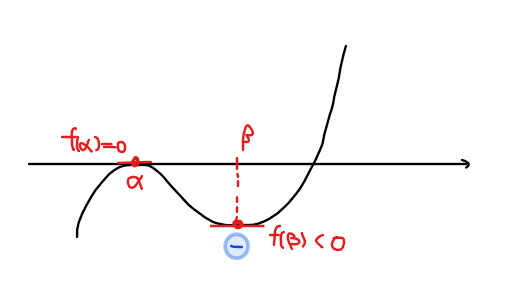
③3次方程式の実数解が1個 ⇔ \(\small f(\alpha)f(\beta)>0\)
*極値が同符号
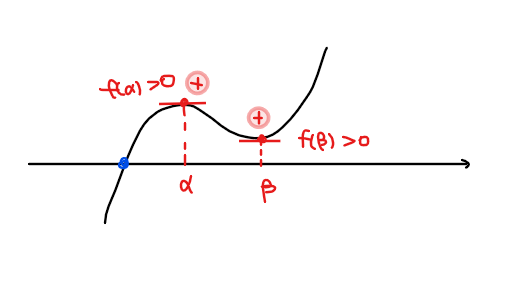
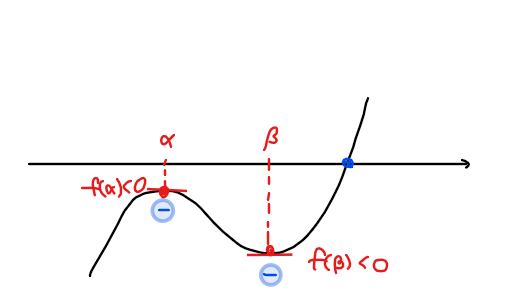
このように3次方程式の解の個数はグラフ上で考えると3次関数と\(\small x\)軸との交点の個数なので、極値の符号に着目してあげることで解の個数を判別することができる。
この判別方法は結果を覚えるというよりは考え方を理解しておいて、なぜこの条件で実数解が判別できるのかを自分の言葉で説明できるようにしておくのがおすすめである。結果だけを暗記しても、実践問題の中で活用するのはなかなか難しい…。
●補足
ちなみに、極値が1つ(\(\small x=\alpha =\beta\))もしくは極値がない場合は、常に実数解は1個であることがグラフをかいてみると分かるので各自確認しておこう。
本記事のまとめ
今回は接線の本数を求める問題について、定数分離を利用した解法と極値条件を利用した解法の2パターンを解説していきました。この2パターンをマスターできれば接線の本数の問題はほとんど解けるはずなので、しっかりと考え方を理解しておきましょう。
最後に本記事のポイントを復習して終わりにしましょう!
☆重要Point☆
・接線の本数を求める方法は
① 定数分離の利用
*接線の本数 ⇒ 方程式の解の個数 ⇒ グラフの交点の個数の問題として解く
② 極値条件の利用
*極値の符号が満たす条件に着目して解の個数を判別せよ!
の2パターン。
・定数分離が使えない場合に極値条件を利用するのがおすすめ!
今回は以上です。お疲れさまでした!








コメント