今回は「少なくとも1つは…であること」、「すべて…であること」の等式証明問題について徹底解説していきます。
等式証明問題としては少し応用問題になりますが、それぞれのキーワードを数式で表すとどうなるのかが理解できれば難しくはないので、苦手意識がある人はぜひ最後までチェックしてみてください!
また、等式証明の基礎として押さえておきたい3つの証明方法については、こちらの記事で詳しく解説しているので、等式証明の基本的な考え方が怪しいなと感じた人はまずはこちらを確認しておきましょう。
- 「少なくとも…」、「すべて…」の等式証明が苦手な人
- 「少なくとも…」、「すべて…」の証明の考え方を理解したい人
- 「少なくとも…」、「すべて…」の等式証明に関する問題演習をしたい人
【問題&解説】「少なくとも…」、「すべて…」の等式証明
【問題1】「少なくとも1つ…」の等式証明(難易度:★★☆)
\(\small xyz=1\)、\(\small x+y+z=xy+yz+zx\)のとき、\(\small x,y,z\)のうち少なくとも1つは1であることを示せ。
\begin{split}
\small \color{#ef5350}{(x-1)(y-1)(z-1)=0}
\end{split}
が成り立つことを示せばよい。詳細は、講義1参照。
\(\small x,y,z\)のうち少なくとも1つが1であることを示すには、\(\small (x-1)(y-1)(z-1)\)を計算した結果が0になること、すなわち
$$\small (x-1)(y-1)(z-1)=0$$
が成り立つことを示せばよい。
ゆえに、
\begin{split}
&\small (x-1)(y-1)(z-1)\\
\small = &\small xyz-xy-yz-zx+x+y+z-1 \quad [*1]\\
\end{split}
\(\small *1\):\(\small (x-1)(y-1)(z-1)\)の展開
\(\small (x-1)(y-1)(z-1)\)の展開は括弧が3つもあって大変ですね。2つの括弧をペアとしてまず展開し、そのあとさらに展開する方法で地道に計算してもOKですが、ここでは一気に展開するコツも紹介しておきます。
一気に展開するコツは、ズバリ、3つの括弧それぞれから1つずつ値を選んで掛け算することです。例えば、3つの括弧すべてから文字を選ぶパターン(\(\small x-1\)の括弧からは\(\small x\)を、\(\small y-1\)の括弧からは\(\small y\)を、\(\small z-1\)の括弧からは\(\small z\)を選んで掛け算)だと\(\small xyz\)という項が出てきます。同様に、3つ括弧から2つの文字を選ぶパターン(\(\small [x,y,-1]\)と\(\small [-1,y,z]\)と\(\small [x,-1,z]\))だと\(\small -xy\)、\(\small -yz\)、\(\small -zx\)の項が出てきます。さらに、3つの括弧から1つの文字しか選ばないパターンだと、\(\small [x,-1,-1]\)と\(\small [-1,y,-1]\)と\(\small [-1,-1,z]\)になるので、\(\small x\)、\(\small y\)、\(\small z\)の項が出てきます。最後に文字を1つも選ばないパターンは\(\small (-1)\times (-1)\times (-1)=-1\)の項です。
このように、各括弧から選ぶ文字数に着目して全パターン(今回だと3つの括弧から2つ項を選ぶ通り数なので\(\small 2^3=8\)通り)を考えていくと、展開した項の値を素早く計算することができます。
ここで、問題文の条件、\(\small xyz=1\), \(\small x+y+z=xy+yz+zx\)を代入すると
\begin{split}
&\small \color{#ef5350}{xyz}-xy-yz-zx+\color{#5c6bc0}{x+y+z}-1\\
\small = &\small \color{#ef5350}1-xy-yz-zx+\color{#5c6bc0}{xy+yz+zx}-1\\
\small = &\small 0\\
\end{split}
よって、\(\small (x-1)(y-1)(z-1)=0\)が成り立つことから、\(\small x-1=0\)または\(\small y-1=0\)または\(\small z-1=0\)より、\(\small x=1\)または\(\small y=1\)または\(\small z=1\)である。
ゆえに、\(\small x,y,z\)のうち少なくとも1つは「1」である(証明終)。
【問題2】「すべて…」の等式証明(難易度:★★☆)
\(\small p+q+r=pq+qr+rp=3\)のとき、実数\(\small p,q,r\)はすべて1であることを示せ。
\begin{split}
&\small \color{#ef5350}{(p-1)^2+(q-1)^2+(r-1)^2=0}
\end{split}
を満たすことを示せばよい。詳細は、講義2を参照。
\(\small p,q,r\)がすべて1であることを示すには、
\begin{split}
&\small (p-1)^2+(q-1)^2+(r-1)^2=0
\end{split}
が成り立つことを示せばよい。
よって、
\begin{split}
&\small (p-1)^2+(q-1)^2+(r-1)^2\\
\small =&\small (p^2-2p+1)+(q^2-2q+1)+(r^2-2r+1)\\
\small =&\small \color{#ef5350}{p^2+q^2+r^2}-2(p+q+r)+3\\
\small =&\small \color{#ef5350}{(p+q+r)^2-2(pq+qr+rp)}-2(p+q+r)+3 \quad [*1]\\
\small =&\small 3^2-2\cdot3-2\cdot 3+3 \quad [*2]\\
\small =&\small 9-6-6+3\\
\small =&\small 0\\
\end{split}
ただし途中式\(\small [*2]\)では問題文の条件 \(\small p+q+r=pq+qr+rp=3\)を用いた。
\(\small *1\):補足
3文字の対称式として有名な関係式なので覚えておきましょう。
$$\small a^2+b^2+c^2=(a+b+c)^2-2(ab+bc+ca)$$
この関係式は展開や因数分解で頻出の
$$\small (a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$$
の公式を覚えていれば簡単に導き出せますね。
今回は、問題文の条件の形を作り出すために\(\small a^2+b^2+c^2\)という形が邪魔なのでこの関係式を利用してうまく消去しています。
よって、\(\small (p-1)^2+(q-1)^2+(r-1)^2=0\)が成り立つことから、\(\small p-1=0\)かつ\(\small q-1=0\)かつ\(\small r-1=0\)より、\(\small p=q=r=1\)が成り立つ。
ゆえに、\(\small p,q,r\)はすべて1である(証明終)。
【問題3】等式証明の応用問題(難易度:★★★)
\(\small x+y+z=0\)、\(\small 2x^2+yz=0\)が成り立つとき、\(\small x\)は\(\small y\)に等しいか、あるいは\(\small x\)は\(\small z\)に等しいことを示せ。
[追手門学院大]
$$\small \color{red}{(A-B)}\color{blue}{\times}\color{red}{(C-D)}=0$$
を示せばよい。詳細は、講義3を参照。
『\(\small x\)が\(\small y\)に等しいまたは、\(\small x\)が\(\small z\)に等しい』ことの証明は、問題解決のKeyに記載の通り
$$\small (x-y)(x-z)=0$$
が成り立つことを示せばよい。
つまり、\(\small (x-y)(x-z)\)を計算してその結果が「0」になることを示す。
\begin{split}
\small (x-y)(x-z) &\small = x^2-\color{red}{(y+z)}x+\color{#435CEC}{yz}\\
\end{split}
ここで、問題文の条件式から
\begin{cases}
\small ①\space x+y+z=0\\
\small \space \Rightarrow \space \color{red}{y+z=-x}\\
\small ②\space 2x^2+yz=0\\
\small \space \Rightarrow \space \color{#435CEC}{yz=-2x^2}\\
\end{cases}
なので、これらを代入することで
\begin{split}
&\small x^2-\color{red}{(y+z)}x+\color{#435CEC}{yz}\\
\small = &\small x^2-\color{red}{(-x)}\cdot x+\color{#435CEC}{(-2x^2)}\\
\small = &\small x^2+x^2-2x^2\\
\small = &\small 0\\
\end{split}
よって、\(\small (x-y)(x-z)=0\)より、その解は
\begin{split}
&\small x-y=0\quad \mathsf{または} \quad x-z=0\\
\small \Leftrightarrow \space &\small ∴ \space \color{red}{x=y \quad \mathsf{または} \quad x=z}\\
\end{split}
ゆえに、\(\small x\)は\(\small y\)に等しいあるいは、\(\small x\)は\(\small z\)に等しい(証明終)。
【徹底解説】「少なくとも…」、「すべて…」の等式証明
【講義1】「少なくとも…」の等式証明の考え方
この問題の難しいポイントは、「少なくとも1つは…」という部分が直感的に数式化しにくいということにあります。どういうことかというと、たとえば『\(\small x\)が1であることを示せ』という証明であれば、証明すべき数式は【\(\small x=1\)】と直観的に明確ですね。でも、『\(\small x,y,z\)の3つ文字のうち、少なくとも1つは1であることを示せ』という証明は「少なくとも1つは1だから、3つの文字のうちどれが1かもわからないし何文字が1があるかも分からない…」となり、結局どんな式を示せばいいんだ?となるわけです。
でも、逆に言うとこれをうまく数式で表せれば、示すべき数式が明確になり、一気に証明しやすくなります。ではここから示すべき数式を考えてみましょう。
それを考えるにあたってヒントになるのが、以下の問題を解くときの考え方です。
(いきなりですが…)問題です。
100個の文字 \(\small x_1,x_2,x_3,\cdots, x_{100}\)には、少なくとも1つは0があります。
では、これらの積 \(\small x_1x_2\cdots x_{100}\)の値はいくつでしょう?
\(\small x_1,x_2,x_3,\cdots, x_{100}\)のどれが「0」かはわかりませんが、全部を掛け算すると少なくともどこかには0が含まれることになるので、積の値は0になります。
では、この問題を解くときに用いた『少なくとも0が1つ含まれる場合、すべてを掛け算した積は0』という考え方を今回の問題に応用できないでしょうか?
すると、たとえば少なくとも「1」が1つ含まれる場合であれば、すべての値から1を引き算してあげた値の中には少なくとも0が1つ含まれることになります。
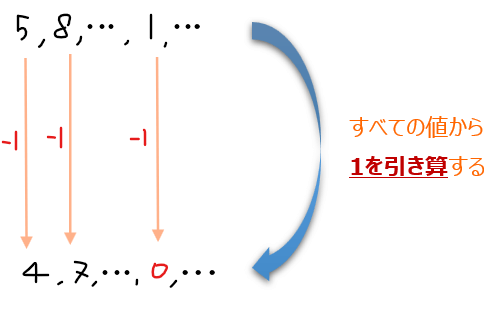
ということは、1を引き算した値をすべてかけ算してあげれば「0」になるので、これが証明すべき数式になります。
よって、一般的に少なくとも「\(\small p\)」が1つ含まれることを示したければ、『各値から\(\small p\)を引き算した値をすべてかけ算すると「0」になる』ことを示せばよいことになります。
●補足:「少なくとも1つ\(\small p\)が含まれる」証明で満たすべき条件式
一般に\(\small n\)個の文字\(\small x_1,x_2,\cdots, x_{n}\)のうち少なくとも1つが\(\small p\)であることを示すには、
$$\small (x_1-p)(x_2-p)\times \cdots \times (x_{n}-p)=0$$
を示せばよい。
【講義2】「すべて…」の等式証明の考え方
今度は「すべてがある値」という証明方法について解説します。これも同じく数式で表現できてしまえば証明できるわけなので、早速どんな数式を満たせばよいのか考えてみましょう。
講義1のときと同様に、まずは『すべての文字の値が「0」』の場合に満たすべき条件を次の例題を参考に考えてみます。
(問題1)
実数\(\small x_1\)が
$$\small (x_1)^2=0$$
を満たすとき、\(\small x_1\)の値を求めよ。
(解答)
答えは、もちろん\(\small x_1=0\)ですね。これは問題ないでしょう。では、次の問題はどうでしょう?
(問題2)
2個の実数 \(\small x_1,x_2\)が
$$\small (x_1)^2+(x_2)^2=0$$
を満たすとき、\(\small x_1,x_2\)の値を求めよ。
(解答)
問題1と比較して、実数が1つ増えました。この問題の答えを考えるには2乗した値が取り得る値について考察することが重要です。
たとえば、\(\small x_1\)が \(\small x_1=3\)のような正の値だったとしましょう。すると、2乗した値も当然\(\small (x_1)^2=9\color{red}{>0}\)となり正の値になります。次に、\(\small x_1\)が \(\small x_1=-2\)のような負の値だったとします。この場合も、2乗した値は\(\small (x_1)^2=4\color{red}{>0}\)で正の値になります。しかし、\(\small x_1=0\)の場合だけ2乗した値も0になります。
つまり、2乗した値は絶対に0以上であり、「0」になるのは元の値が0のときだけになります。
\begin{split}
\small (x_1)^2=
\begin{cases}
\small 0 &\space \color{red}{(x_1=0 \mathsf{のとき})}\\
\small \color{red}{\mathsf{正の値}} &\space \color{red}{(x_1 \neq 0 \mathsf{のとき})}
\end{cases}
\end{split}
もちろんこれは\(\small x_2\)でも同じことが言えます。
よって、『2乗した値は絶対に0以上であり、「0」になるのは元の値が0のときだけ』ということを踏まて問題の左辺をみると、『\(\small (x_1)^2+(x_2)^2 =\)(0以上の値)+(0以上の値)=(0以上の値)』(0以上の値の和も当然0以上)になります。ですが、右辺見ると「0」になっています。ということは、\(\small (x_1)^2、(x_2)^2\)のいずれかが正の値だと絶対に和が0にはならない[*1]ので、どちらも「0」であることが分かります。
\(\small *1\):補足
たとえば、\(\small x_1\)が正の値の場合、『\(\small (x_1)^2+(x_2)^2 =\)(正の値)+(0以上の値)=(正の値)≠0』となり、右辺は絶対に0にならないということ。
もっと具体的な例で理解したい人は、\(\small x_1、x_2\)に具体的な値を入れて0になる組み合わせを探してみるのがおすすめ。\(\small x_1=x_2=0\)の場合以外は、絶対に0にならないことが感覚的に理解できるだろう。
よって
\begin{split}
&
\begin{cases}
\small (x_1)^2=0\\
\small (x_2)^2=0\\
\end{cases}
\small \quad \color{red}{\mathsf{◀問題}1\mathsf{に帰着}}\\
\Leftrightarrow \space &
\begin{cases}
\small x_1=0\\
\small x_2=0\\
\end{cases}
\end{split}
よって、\(\small x_1=x_2=0\)が答えです。
(最終問題)
100個の実数 \(\small x_1,x_2,x_3,\cdots, x_{100}\)が
$$\small (x_1)^2+(x_2)^2+\cdots+(x_{100})^2=0$$
を満たすとき、これらの実数の値を求めよ。
問題2の応用ですが、2乗した値は絶対に0以上であり、「0」になるのは元の値が0のときだけという性質を考えると答えは、\(\small x_1=x_2=\cdots =x_{100}=0\)ですね。結局、\(\small x_1~x_{100}\)のどれか1つでも0以外の値だと2乗した値が正の値になってしまい、全体の和が0にならないというわけです。
さて、だいぶ話が逸れましたが、本題に戻ります。3つの問題を考えてもらったわけですが、これらの問題からわかったこととしては、
すべての文字が「0」であること ⇔ 各文字の2乗の和が「0」になること
です。この考え方を利用すると「すべてがある値」になることを証明する際に満たすべき数式が分かります。考え方自体は講義1のときと同じで、すべてがある値(たとえば \(\small p\))であることを示したければ、各値から\(\small p\)を引き算した値はすべて「0」になるはずなので、それぞれ2乗した和が「0」になればよいという先程の考え方が使えます。
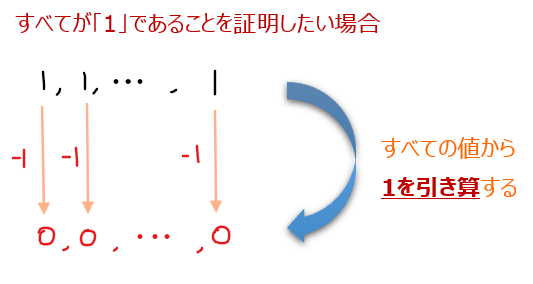
若干日本語で書くと満たすべき数式が複雑ですが、具体例で考えると\(\small x,y,z\)のすべてが2であることを証明したければ、
$$\small (x-2)^2+(y-2)^2+(z-2)^2=0$$
を示せばよいことになります。
●補足:「すべてが\(\small p\)になる」証明で満たすべき条件式
一般に\(\small n\)個の文字\(\small x_1,x_2,\cdots, x_{n}\)のすべてが\(\small p\)であることを示すには、
$$\small (x_1-p)^2+(x_2-p)^2+\cdots +(x_{n}-p)^2=0$$
を示せばよい。
【講義3】いずれかの条件を満たすことの証明
応用問題として複数の条件のいずれかを満たすことを証明する問題の考え方のコツを解説します。
早速ですが、考え方のコツはズバリ以下2点を駆使して条件式を組み立てることです。
①等式条件は必ず『(右辺)\(\small =0\)』で表せる。
②\(\small AB=0\)の解は、『\(\small A=0\)または\(\small B=0\)』
まず①は言葉にすると難しく見えますが、言っていること自体は大したことはなくって、等式条件というのは「イコール(=)」の関係式で表せる条件のことなので、イコールで表せる関係式は必ず右辺を「\(\small =0\)」にできるということを言っているだけです。たとえば適当に「\(\small x+y=xy+2z\)」という関係式があれば右辺の文字を全部左辺に移項してあげれば、「\(\small x+y-xy-2z\color{red}{=0}\)」というように「(右辺)=0」にできます。よって、すべての等式条件は「(右辺)=0」と表せます。
次に②もかけ算した答えが「0」ならば、どれかが「0」だということを言っているだけです。逆に言えば、どれかが「0」であればよいことを示したければ、『それらの積=0』を示せばよいわけです。
ということで、この①と②の両方を組み合わせると、複数の等式条件を満たすことを証明したい場合は、次の2ステップで証明すべき等式を組み立てればよいことになります。
・STEP2:『「STEP1の左辺」を掛け算した式=0』を示す
②で確認した通り、「STEP2を示すこと ⇔ 複数の等式条件のいずれかを満たすこと」になるので、この考え方で証明することができます。
最後にイメージアップのために、具体例を確認して理解度を深めましょう。
(問題)
\(\small x=y\)または\(\small z=1\)であることを証明するためにはどんな式を満たすことを証明できればよいか答えよ。
(解答)
\begin{cases}
\small 条件1:x=y\\
\small 条件2:z=1\\
\end{cases}
まずSTEP1として、条件1、2を「(右辺)=0」の形にします。
≪条件1≫
\(\small x-y=0 \quad \cdots①\)
≪条件2≫
\(\small z-1=0 \quad \cdots②\)
最後に、STEP2より、満たすべき条件式は①、②の条件の積=0としてあげればよいので
$$\small \color{red}{(x-y)(z-1)=0}$$
を示せばよい。
●補足
逆に、上記の式 \(\small (x-y)(z-1)=0\)を満たす場合、その解は
\begin{split}
&\small x-y=0 \quad または\quad z-1=0\\
\small \Leftrightarrow &\small \quad x=y \quad または \quad z=1\\
\end{split}
となり、条件1または条件2を満たすことが示せることが分かる。
本記事のまとめ
今回は等式証明の応用問題として、「少なくとも1つがある値であることの証明」と「すべてがある値になることの証明」を中心にその思考法を徹底解説していきましたがいかがでしたか?
この2パターンは大学入試や定期テストでもよく出る定番問題になるので、是非考え方を理解して解けるようにしておきましょう。
最後に本記事の要点を復習して終わりにしましょう。
☆重要ポイント
・「少なくとも1つ「\(\small p\)」が含まれる」、「すべてが「\(\small p\)」である」ことの証明は、その特殊形である「少なくとも1つは0が含まれる証明」、「すべてが0である証明」の考え方を利用せよ!
●「少なくとも1つは0」が含まれることの証明(特殊形)
・各文字の積が「0」を示せばよい。
●「すべてが0」であることの証明(特殊形)
・各文字の2乗の和が「0」を示せばよい。
・一般形は、各値から「\(\small p\)」を引き算することで特殊形に帰着できる。
●「少なくとも1つは\(\small p\)」が含まれることの証明(一般形)
・各文字から\(\small p\)を引き算した値の積が「0」を示せばよい。
●「すべてが\(\small p\)」であることの証明(一般形)
・各文字から\(\small p\)を引き算した値の2乗の和が「0」を示せばよい。
では今回はここまでです。お疲れさまでした!




コメント