【3次元の魔法陣！？】立方陣の1列の和を高校数学で計算してみた（数列の応用問題）

皆さん、魔法陣は知ってますか？

小学校の算数で習って覚えている人もいるのではないでしょうか？

魔法陣とは、縦横斜めのマスを足し算した値がすべて同じ値になるように正方形上に数字を配置したもので、例えば1辺の長さが「3」の魔法陣（3×3の魔法陣）であれば、以下のようなものです。

マス目の数字をよく見ると、縦横斜めのすべての列の和が15になっています。

魔法陣は1辺の長さが長くなるほど作るのが難しくなりますが、とはいえ2次元の話なのでまだイメージがしやすいですね。

では、この魔法陣を3次元にしたらどうでしょうか…？ちょっとイメージするのが大変ですが、縦横斜めに加えて、上下や立体的な斜めの和も同じになるような考慮をしないといけません[*1]。

ということで、今回は立方陣に関する問題を高校数学の数列を利用して考えていきたいと思います！ゆっくりのんびりとしたテンションでご覧ください！

*1：立方陣の存在について
立方陣の定義自体は、記載した通りで端的に表現すれば魔法陣の3次元拡張版だが、果たしてそんな立方陣が存在するのかというと必ずしもそうではない。
たとえば2×2×2の立方陣は存在しないし、3×3×3の立方陣は、上下・左右・前後・斜めのすべての列の和が同じ値になるものはなく一部だけ同じになるものが存在する。
一方で、すべての列が和が同じになる立方陣もしっかり存在しており、5×5×5、6×6×6、7×7×7などの立方陣があることが知られている。

【問題】立方陣の1列の和
【予備知識】立方陣の性質
【解説＆解答】立方陣の1列の和の求め方
本記事のまとめ

【問題】立方陣の1列の和

【数B】立方陣の1列の和（数列の超難問）

1辺の和が$\small 50000050$である立方陣の1辺の長さを求めよ。

【予備知識】立方陣の性質

本問題を攻略するうえでは、数列計算の知識はさることながら、立方陣についての最低限の知識も必要となるのではじめに簡単に確認しておこう。

問題解決のKey

立方陣の性質をうまく利用して数列計算する。
【立方陣の性質】
・性質1：上下・左右・前後・斜めのすべての列の和が等しい
・性質2：1～マス目の数の数字を1回ずつ、すべて利用する

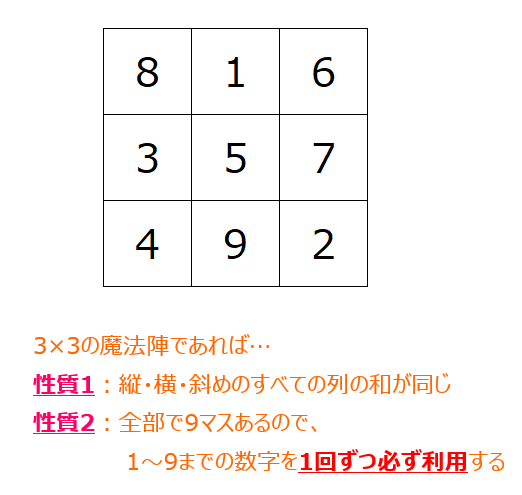
性質1は冒頭にも触れているのでよいだろう。性質2は自明すぎて意外と忘れがちな性質だが、魔法陣の時と同様、マス目の数字は1から順番にマス目の数までの数字を1回ずつ使用することがルールになる。たとえば、途中で同じ数字を2回以上使ったり、1度も使われない数字があってはいけないということだ。

これはもし仮に同じ数字を何回でも利用できるならば、すべてのマスを同じ数字にすれば必ず性質1を満たす立方陣が無限に作れるためである。

【解説＆解答】立方陣の1列の和の求め方

求める立方陣の1辺の長さを$\small n$とおき、$\small n \times n \times n$の立方陣を考えることにする。問題を解く方針としては、1列の和を$\small n$で表して$\small 50000050$とイコールで結ぶことで方程式を解く流れで考えていく。

では、まずは1列の和から求めていこう。1列の和を$\small p$とおく。和を計算するうえで立体的に考えるのは難しいので、とある段（仮に$\small m$段目（もちろん$\small 1≦m≦n$）としよう）に着目して考えていく。

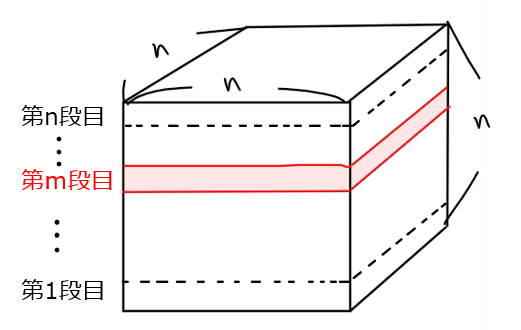
すると第$\small m$段だけを見るとこれは$\small n \times n$の魔法陣そのものになっている。第$\small m$段にあるマス目は全部で$\small n \times n = n^2$個なので、それぞれのマスにある数字を左上から順番に

\begin{split}
\small a_{m,1}、a_{m,2}、a_{m,3}、\cdots、a_{m,n^2-1}、a_{m,n^2}
\end{split}

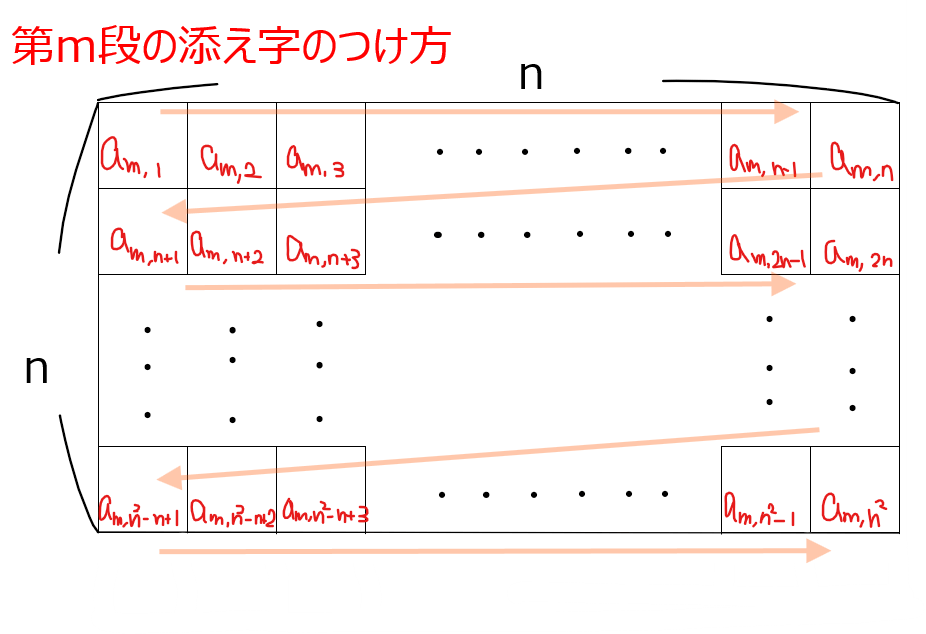
とおく[*1]と、第$\small m$段目のマス目の総和、すなわち$\small a_{m,1}～ a_{m,n^2}$の和は

\begin{split}
\small a_{m,1}+a_{m,2}+\cdots+a_{m,n^2-1}+a_{m,n^2}=np \quad \cdots ①
\end{split}

が成り立つ。

*1：$\small a_{x,y}$の添え字の意味について
添え字の意味としては、$\small x$が第何段目にあるか、$\small y$が左上から何番目のマスの数字かを表している。なので、今回であれば、第$\small m$段目に着目しているので、$\small x=m$となり、$\small y$は順番に$\small 1,2,\cdots,n^2-1,n^2$のように$\small n^2$個のマス目の何番目にあるかを表すことができる。よって、このルールに沿って添え字を決めると立方陣の第何段目のどの位置の数字かを一意的に表すことができる。

式①の右辺ってどこからでてきたの！？と驚いた人も多いと思うので、ここからなぜ式①が成り立つのかについて少し解説する。

今考えている立方陣の例だと文字が多くなって抽象的になってしまうので、まずは冒頭に紹介した3×3の魔法陣を例として考え方から理解するのがよいだろう。

今、上記の魔法陣の1列の和を$\small p$とおき（実際には1列の和は15なので$\small p=15$となるが一旦文字で置いておく）、マスの数字も先程と同様に左から順番に

\begin{split}
\small a_{1,1}、a_{1,2}、a_{1,3}、\cdots、a_{1,8}、a_{1,9}
\end{split}

とおく。ただし、2次元の魔法陣なので段数は1段のみのため、$\small m=1$としている。文字で置いたので複雑に感じるかもしれないが、$\small a_{1,1}=8、a_{1,2}=1、a_{1,3}=6、a_{1,4}=3\space \cdots$といった具合に対応している。

ここで、この魔法陣のマス目の総和、すなわち$\small a_{1,1}～a_{1,9}$までのすべての和というのは、『上段の和＋中段の和＋下段の和』のことなので、1列の和が$\small p$であることから合計は$\small 3p$であることが分かる。

\begin{split}
\small (a_{1,1}～a_{1,9}\mathsf{までの和}) & \small =\color{red}{a_{1,1}+a_{1,2}+a_{1,3}}\\
&\quad \small \color{blue}{+a_{1,4}+a_{1,5}+a_{1,6}}\\
&\qquad \small \color{green}{+a_{1,7}+a_{1,8}+a_{1,9}}\\
&\small =\color{red}{p}+\color{blue}{p}+\color{green}{p}\\
&\small = 3p\\
\end{split}

ちなみに、合計である$\small 3p$の「3」は、上段、中段、下段の3段の「3」なので、一般に$\small n \times n$の魔法陣であればその総和は$\small np$（＝$\small n$段）になるということで、これが式①の右辺そのものである。

では、改めて第$\small m$段目のマスの総和が

\begin{split}
\small a_{m,1}+a_{m,2}+\cdots+a_{m,n^2-1}+a_{m,n^2}=np \quad (\mathsf{式①の再掲})
\end{split}

で表されることから、$\small n \times n \times n$の立方陣では、第1段～第$\small n$段まで$\small n$個の段があるので、他の段についても同様の計算ができる。

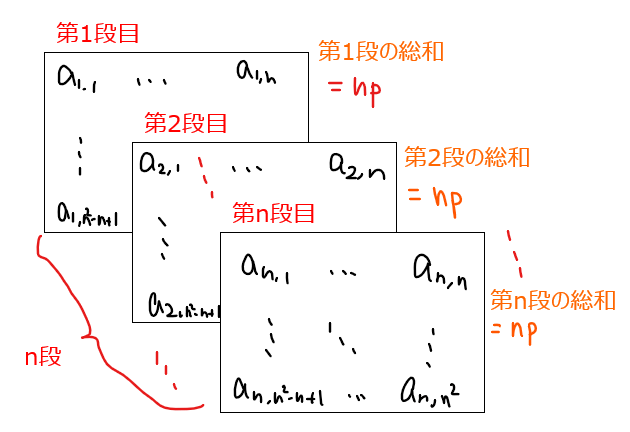
\begin{split}
\small \mathsf{第}\color{red}1\mathsf{段の総和：}&\small a_{\color{red}1,1}+a_{\color{red}1,2}+\cdots+a_{\color{red}1,n^2-1}+a_{\color{red}1,n^2}=np\\
\small \mathsf{第}\color{red}2\mathsf{段の総和：}&\small a_{\color{red}2,1}+a_{\color{red}2,2}+\cdots+a_{\color{red}2,n^2-1}+a_{\color{red}2,n^2}=np\\
&\vdots\\
\small \mathsf{第}\color{red}n\mathsf{段の総和：}&\small a_{\color{red}n,1}+a_{\color{red}n,2}+\cdots+a_{\color{red}n,n^2-1}+a_{\color{red}n,n^2}=np\\
\end{split}

ここで上記の等式を全て足し合わせると、左辺は$\small a_{1,1}～a_{n,n^2}$までの全マスの値の総和になる[*2]。

*2：補足
（第1段目の総和）+（第2段目の総和）＋…＋（第n段目の総和）になるので、$\small n \times n \times n$の立方陣にあるすべてのマス目の値を足し算した値になる。

一旦、第1段目の総和～第$\small n$段目の総和の等式を足し合わせた式を記載しておくと

\begin{split}
&\small a_{\color{red}1,1}+a_{\color{red}1,2}+\cdots+a_{\color{red}n,n^2-1}+a_{\color{red}n,n^2}=n^2p \quad \cdots②\\
\end{split}

ちなみに、右辺は$\small np$が全部で$\small n$個あるだけなので、$\small np \times n = n^2p$で計算できることに注意する。

式②の左辺について、$\small a_{1,1}～a_{n,n^2}$のそれぞれの値自体は分からないが、予備知識の立方陣の性質2より、$\small a_{1,1}～a_{n,n^2}$は1～$\small n^3$までのいずれかの数字が1回ずつ登場していることは確かなので、

\begin{split}
&\small a_{\color{red}1,1}+a_{\color{red}1,2}+\cdots+a_{\color{red}n,n^2-1}+a_{\color{red}n,n^2}\\
&\small =1+2+\cdots + (n^3-1)+n^3 \quad [*3]\\
&\small =\frac{1}{2}n^3(n^3+1) \quad [*4]\\
\end{split}

*3：補足
$\small a_{\color{red}1,1}+a_{\color{red}1,2}+\cdots+a_{\color{red}n,n^2-1}+a_{\color{red}n,n^2}$の和の各項は、1～$\small n^3$までの値が1個ずつ含まれた和なので、適当に和の順序を入れ替えることで1～$\small n^3$の順番にできる。
イメージが湧きにくければ、3×3の魔法陣を例に実際に計算してみると

\begin{split}
&\small a_{1,1}+a_{1,2}+a_{1,3}\\
&\small +a_{1,4}+a_{1,5}+a_{1,6}\\
&\small +a_{1,7}+a_{1,8}+a_{1,9}\\
\small =&\small 8+1+6\\
&\small +3+5+7\\
&\small +4+9+2\\
\small =&\small 1+2+3+4+5\\
&\small +6+7+8+9\\
\end{split}
のように、並び替えることで1～9の和にできることが分かるだろう。

*4：等差数列の公式
初項$\small a$、末項$\small \ell$、項数$\small n$の等差数列の和は
$$\small \frac{1}{2}n(a+\ell)$$
となることを用いると、[*3]は初項1、末項 $\small n^3$、項数 $\small n^3$の等差数列の和として求めることができる。

この結果を式②の左辺に代入することで

\begin{split}
&\small \frac{1}{2}n^3(n^3+1)=n^2p\\
\small \Leftrightarrow \space &\small \frac{1}{2}n(n^3+1)=p\\
\end{split}

最後に、今回求めたい1辺の長さである$\small n$を求めていこう。問題文から$\small p=50000050$を代入することで

\begin{split}
&\small \frac{1}{2}n(n^3+1)=50000050 \quad \cdots③\\
\small \Leftrightarrow \space &\small n(n^3+1)=100000100\\
\small \Leftrightarrow \space &\small n^4≒100000000\\
\small \Leftrightarrow \space &\small n^4=10^8\\
\small \Leftrightarrow \space &\small n=10^2 \quad [*5]\\
\end{split}

*5：補足
最後の$\small n$の4次方程式はまともに解くのは大変なので、右辺の数が大きいことと$\small n$は自然数であることから、ある程度簡略化して類推して解くという解法が効果的である。

$\small n=100$を③の左辺に代入すると、確かに右辺と一致することから$\small n=100$が解であることが分かった。

よって、1辺の長さが100の立方陣…（答）である。