三角関数の合成を利用した最大値・最小値の求め方（角度が分からないパターンも解説）

今回は、三角関数の合成を使って最大値・最小値を求める問題を解説します。特に、合成後に出てくる角度が具体的な値で求まらず、\(\small \alpha\)などの文字でおいて解く問題の場合、「解き方の流れがつかめない…」「どうやって最大値・最小値を調べればいいの？」と迷ってしまう人も多いはずです。

本記事では、そうしたケースでも迷わず解けるように、考え方のポイントと解法の流れを分かりやすく解説していきます。

• 三角関数の合成を使って最大値・最小値を求める方法をしっかり理解したい人
• 角度が具体的に求まらないタイプの問題（\(\small \alpha\)とおく問題）の解き方に不安がある人
• 定期テストや大学入試に向けて、三角関数の得点力を上げたい人

【問題＆解説】三角関数の合成を利用した最大値・最小値の求め方

【問題1】角度が求まるパターン（難易度：★☆☆）

\(\small \sin\)と\(\small \cos\)の和の形で角度部分が\(\small \theta\)に揃っていることから、三角関数の合成公式を用いて\(\small \sin\)の形に統一します。

三角関数の合成より

\begin{split}
\small y &\small =\sin \theta +\sqrt{3}\cos \theta\\
&\small = \color{#ef5350}{2\sin \left(\theta + \frac{\pi}{3}\right)} \quad \color{#ef5350}{◀三角関数の合成}\\
\end{split}

【補足】三角関数の合成ってどうやるの？
\(\small \sin \)の係数を\(\small x\)座標、\(\small \cos\)の係数を\(\small y\)座標に持ってきたときの\(\small x\)軸からの角度が合成後の角度、斜辺の長さが合成後の\(\small \sin\)の係数になります。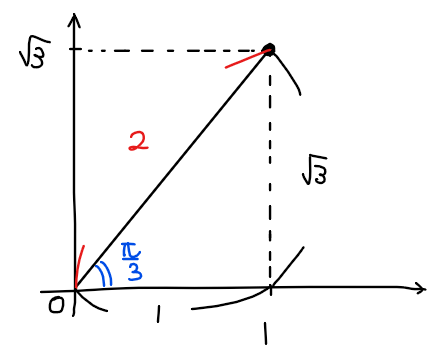

「三角関数の合成の方法が分からない…」という人は、三角関数の合成公式｜証明と使い方をわかりやすく解説【cos の合成にも対応】で合成公式と使い方を解説しているので、参考にしてみてください！

三角関数を合成すると角度部分が\(\small \displaystyle \theta + \alpha\)の形になるので、丸ごと文字で置き換えしておくと、このあとの最大値・最小値の計算が考えやすくなります。

本問であれば、\(\small \displaystyle t= \theta+\frac{\pi}{3}\)…①と置き換えて

\begin{split}
\small y =2\sin t \space \cdots ②\\
\end{split}

の最大・最小を求める問題として考えていきます。

文字の置き換えをしたときは、置き換えた文字が取り得る範囲もあわせて確認しておきましょう（特に角度の範囲が\(\small 0≦\theta<2\pi\)よりも狭い範囲に制限されている場合、変数の範囲を確認しておかないと正しい答えが出せません）。

\(\small 0≦\theta<2\pi\)と①の関係式から、置き換えた文字 \(\small t\)の範囲は

\begin{split}
&\small 0≦\theta<2\pi\\
\small \Leftrightarrow \space &\small \color{#ef5350}{\frac{\pi}{3}}≦\theta \color{#ef5350}{+\frac{\pi}{3}}<2\pi\color{#ef5350}{+\frac{\pi}{3}}\\
\small \Leftrightarrow \space &\small \frac{\pi}{3}≦t<2\pi+\frac{\pi}{3} \space \cdots ③\\
\end{split}

ではここから、単位円を用いて最大値と最小値を求めていきます。求める値②は\(\small 2\sin t\)なので、\(\small \sin\)の値（単位円の縦軸）が\(\small t\)の値によってどう変わるかを単位円上で確認できればOKです。単位円を描くときには③で求めた\(\small t\)の値の範囲もわかるようにしておきましょう。

【補足】単位円と\(\small \sin \)、\(\small \cos \)の値の関係
下図のように、単位円（半径が1の円のこと）では三角形の斜辺が1になるので、横軸の値が\(\small \cos\)の値、縦軸の値が\(\small \sin\)の値になります。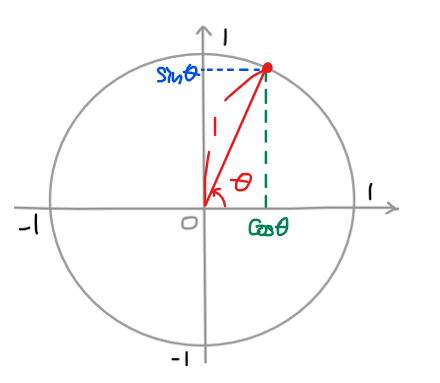

\(\small \sin t\)と③の範囲を単位円上に図示すると下図のようになります。

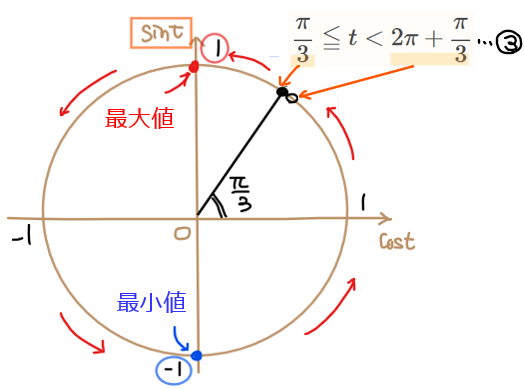
③の範囲は、\(\small \displaystyle t=\frac{\pi}{3}\)からスタートして\(\small \displaystyle t=2\pi+\frac{\pi}{3}\)までの一周分になります。

『\(\small \sin\)の値＝単位円の縦軸の値』だったことを思い出すと、\(\small \sin t\)の値の最大・最小は、単位円上の縦軸の値の最大・最小を確認してあげればよいので、図を見てあげると赤丸箇所で最大値\(\small 1\)、青丸箇所で最小値\(\small -1\)を取ることが分かります。

また、最大値での\(\small t\)の値（角度の値）は単位円から \(\small \displaystyle t=\frac{\pi}{2}\)、最小値での\(\small t\)の値は \(\small \displaystyle t = \frac{3}{2}\pi\)であることも分かります。

ここまでの結果をまとめると、

・\(\small \sin t\)の最大値：\(\small \displaystyle 1 \space \left(t = \frac{\pi}{2}\right)\)
・\(\small \sin t\)の最小値：\(\small \displaystyle -1 \space \left(t = \frac{3}{2}\pi\right)\)

となります。今回求めたかったのは②の\(\small 2\sin t\)の最大値、最小値だったので、上の結果を2倍してあげることで

・\(\small \color{red}2\sin t\)の最大値：\(\small \displaystyle \color{red}2 \space \left(t = \frac{\pi}{2}\right)\)
・\(\small \color{red}2\sin t\)の最小値：\(\small \displaystyle \color{red}{-2} \space \left(t = \frac{3}{2}\pi\right)\)

と求めることができます。

最後に最大値、最小値をとるときの値が\(\small t\)の値になっており、\(\small t\)は自分で勝手に設定した文字なので、問題にある\(\small \theta\)の値に直してあげれば完成です。

①で\(\small \displaystyle t=\theta+\frac{\pi}{3}\)とおいていたので、最大値をとるときの\(\small \theta\)の値は、\(\small \displaystyle t=\frac{\pi}{2}\)を①に代入することで

\begin{split}
&\small \theta+\frac{\pi}{3}=\frac{\pi}{2}\\
\small \Leftrightarrow \space &\small \color{#ef5350}{\theta=\frac{\pi}{6}}.\\
\end{split}

同様に、最小値をとるときの\(\small \theta\)の値は、\(\small \displaystyle t=\frac{3}{2}\pi\)を①に代入することで

\begin{split}
&\small \theta+\frac{\pi}{3}=\frac{3}{2}\pi\\
\small \Leftrightarrow \space &\small \color{#ef5350}{\theta=\frac{7}{6}\pi}\\
\end{split}

と求めることができます。

（解答）
\(\small \displaystyle \theta = \frac{\pi}{6}\)のとき、最大値\(\small 2\)をとり、\(\small \displaystyle \theta = \frac{7}{6}\pi\)のとき、最小値\(\small -2\)をとる。

●解法の発想
三角関数の和になっている問題は、そのままだと単位円を使った最大値・最小値の確認ができないので、\(\small \sin\)または\(\small \cos \)のどちらかに統一して解くのが定石です。
→\(\small \sin/\cos\)を統一するときに三角関数の合成を使うと考えよう。

【問題2】角度が求まらないパターン（難易度：★★☆）

三角関数の合成について、斜辺は三平方の定理から\(\small \sqrt{1^2+2^2}=\sqrt{5}\)と求まりますが、一方で角度については我々が知っている特殊な三角形ではないので求めることができません。

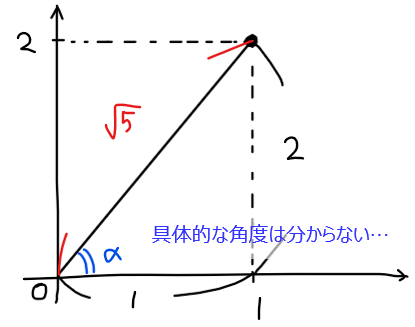
具体的な角度が分からない場合は、とりあえず角度を\(\small \theta = \alpha\)のように文字でおいておきます。\(\small \alpha\)がどんな角度かは図を見れば分かりますが、数式的に説明したければ、角度の大きさは三角比を使って説明すればよいので、

\begin{split}
\small \sin \alpha= \frac{2}{\sqrt{5}}, \space \cos \alpha = \frac{1}{\sqrt{5}} \space \cdots ①
\end{split}

を満たす角度と記述しておけばよいでしょう。

よって、問題の三角関数は①を満たす角度\(\small \alpha\)を用いて

\begin{split}
\small y &\small =\sin \theta +2\cos \theta\\
&\small =\color{#ef5350}{\sqrt{5}\sin \left(\theta +\alpha \right)}\\
\end{split}

のように合成することができます。

角度部分を\(\small t= \theta +\alpha\)…②のように置き換えすると、求める関数 \(\small y=\sin \theta + 2\cos \theta\)は

\begin{split}
\small y &\small =\sqrt{5}\sin t \space \cdots ③\\
\end{split}

と置き換えができます。よって、③の最大値・最小値を求めることを考えていきます。

②で置き換えた文字\(\small t\)の範囲を確認すると

\begin{split}
&\small 0≦\theta<2\pi\\
\small \Leftrightarrow \space &\small \color{#ef5350}{\alpha}≦\theta \color{#ef5350}{+\alpha}<2\pi\color{#ef5350}{+\alpha}\\
\small \Leftrightarrow \space &\small \alpha ≦t<2\pi+\alpha \space \cdots ④\\
\end{split}

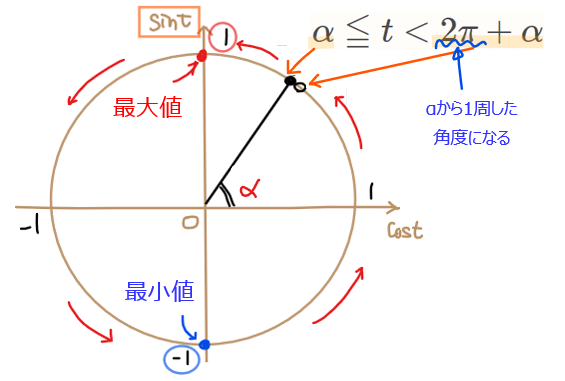
よって、単位円上では上記の範囲が\(\small t\)の範囲になる（*1）ので、\(\small \sin t\)は、\(\small \displaystyle t = \frac{\pi}{2}\)で最大値\(\small 1\)、\(\small \displaystyle t = \frac{3}{2}\pi\)で最小値\(\small -1\)をとることが分かります。

*1：【補足】置き換えた文字の範囲について
もともとの角度\(\small \theta\)の範囲が\(\small 0≦ \theta < 2\pi\)で単位円上を1周する範囲になっているので、\(\small t = \theta +\alpha\)のような置き換えをした場合は、範囲の開始位置と終了位置が\(\small +\alpha\)だけズレるだけで単位円上を1周する範囲になることは変わりません。

故に、③の\(\small \sqrt{5}\sin t\)の最大値・最小値は、全体を\(\small \sqrt{5}\)倍することで\(\small \displaystyle t = \frac{\pi}{2}\)で最大値\(\small \sqrt{5}\)、\(\small \displaystyle t = \frac{3}{2}\pi\)で最小値\(\small -\sqrt{5}\)となります。

最後に、②の関係式 \(\small t = \theta +\alpha \)を使って、角度 \(\small t\)を\(\small \theta\)に戻します。

最大値をとるときの角度 \(\small \displaystyle t = \frac{\pi}{2}\)を②に代入すると

\begin{split}
&\small \theta+\alpha =\frac{\pi}{2}\\
\small \Leftrightarrow \space &\small \color{#ef5350}{\theta=\frac{\pi}{2}-\alpha}\\
\end{split}

という感じで\(\small \theta\)を求めようとすると、ここにきて\(\small \alpha\)の具体的な値が分からず計算が行き詰ってしまいます…。このような場合は、具体的な角度 \(\small \theta\)は求めることができないので、代わりに\(\small \sin \theta , \space \cos \theta\)の値を求めてあげればOKです。

では、最大値をとるときの\(\small \sin \theta\), \(\small \cos \theta\)の値を求めていきます。\(\small \displaystyle \theta = \frac{\pi}{2}-\alpha\)より、

\begin{split}
\small \sin \theta &\small \displaystyle = \sin \left( \frac{\pi}{2}-\alpha \right)\\
&\small \displaystyle = \cos \alpha\\
&\small \displaystyle = \color{red}{\frac{1}{\sqrt{5}}} \space (∵①)\\
\end{split}

\begin{split}
\small \cos \theta &\small \displaystyle = \cos \left( \frac{\pi}{2}-\alpha \right)\\
&\small \displaystyle = \sin \alpha\\
&\small \displaystyle = \color{red}{\frac{2}{\sqrt{5}}} \space (∵①)\\
\end{split}

同様に、最小値をとるときの\(\small \sin \theta\), \(\small \cos \theta\)の値は、\(\small \displaystyle \theta = \frac{3}{2}\pi-\alpha\)より、

\begin{split}
\small \sin \theta &\small \displaystyle = \sin \left( \frac{3}{2}\pi-\alpha \right)\\
&\small \displaystyle = -\cos \alpha\\
&\small \displaystyle = \color{blue}{-\frac{1}{\sqrt{5}}} \space (∵①)\\
\end{split}

\begin{split}
\small \cos \theta &\small \displaystyle = \cos \left( \frac{3}{2}\pi-\alpha \right)\\
&\small \displaystyle = -\sin \alpha\\
&\small \displaystyle = \color{blue}{-\frac{2}{\sqrt{5}}} \space (∵①)\\
\end{split}

以上より、問題の関数は、\(\small \displaystyle \sin \theta = \frac{1}{\sqrt{5}}\), \(\small \displaystyle \cos \theta = \frac{2}{\sqrt{5}}\)のとき最大値 \(\small \sqrt{5}\)、\(\small \displaystyle \sin \theta = -\frac{1}{\sqrt{5}}\), \(\small \displaystyle \cos \theta = -\frac{2}{\sqrt{5}}\)のとき最小値 \(\small -\sqrt{5}\)をとる…【答】。

本記事のまとめ

この記事では、三角関数の合成を利用した最大値・最小値の求め方について、合成後の角度が具体的に求まるパターンと求まらないパターンの両方を解説しました。

三角関数の最大・最小は

• 置き換え
• 範囲の確認
• 単位円での把握
• 角度の戻し

と手順が多いため、最初は混乱しやすい分野です。
しかし、「なぜこの手順をするのか」 を意識して一つずつ確認することで、確実に理解を深めることができます。

三角関数の合成と最大値・最小値は、入試でもテストでも頻出の重要分野です。
ぜひ今回の流れを繰り返し練習して、確かな得点源にしていきましょう！

今回は以上です。お疲れさまでした！