今回は三角関数を含む不等式(三角不等式)の解き方について解説していきます。三角方程式であれば解けるけど、不等式になった途端解き方が分からなくなる…という人は結構多いです。そこで本記事では、単位円を利用した三角関数を含む不等式の解き方のコツを全パターン徹底解説していきます。応用問題への基礎にもなる重要な考え方になるので、一緒に苦手を克服していきましょう!
- 単位円を使って三角関数を含む不等式を解くコツを知りたい人
- 三角関数を含む不等式の基本問題が解けるようになりたい人
- 三角関数を含む不等式の応用問題を解くための基礎作りがしたい人
- 定期テスト対策がしたい人
【問題&解説】単位円を利用した三角関数を含む不等式の解法
#三角関数を含む不等式の基本問題は全12パターン
\(\small \sin\theta\)、\(\small \cos\theta\)、\(\small \tan\theta\)の3種類×各々4つのバリエーション(※)=全12パターン(※不等号の向きと値の符号(正or負)の組合せの4パターン)を本記事では解説していきます。
【問題1】\(\small \sin\theta\)に関する不等式の解き方(難易度:★★☆)
\(\small 0≦\theta < 2\pi\)のとき、次の不等式を解け。
(1)\(\small \displaystyle \sin\theta >\frac{1}{\sqrt{2}}\)
(2)\(\small \displaystyle \sin\theta ≧-\frac{1}{2}\)
(3)\(\small \displaystyle \sin\theta <-\frac{1}{2}\)
(4)\(\small \displaystyle \sin\theta <\frac{\sqrt{3}}{2}\)
・STEP1:単位円を描き問題の不等式が満たす領域を図示
*単位円上では\(\small \sin\theta\)は \(\small y\) の値、\(\small \cos\theta\)は \(\small x\) の値に相当する。
・STEP2:スタート地点からSTEP1で図示した領域を満たす単位円上の部分を図示
*本問のように角度の範囲が\(\small 0≦\theta<2\pi\)であれば、\(\small \theta =0\)がスタート、\(\small \theta=2\pi\)がゴール
・STEP3:STEP2で求めた範囲の端点となる角度を求める
解き方の流れは(1)~(4)で共通であり、以下の3ステップで考えていくとよい。
まずは、単位円を描き、不等式 \(\small \displaystyle y>\frac{1}{\sqrt{2}}\)の範囲を図示する(\(\small \sin\theta\)は\(\small y\)の値のため)。
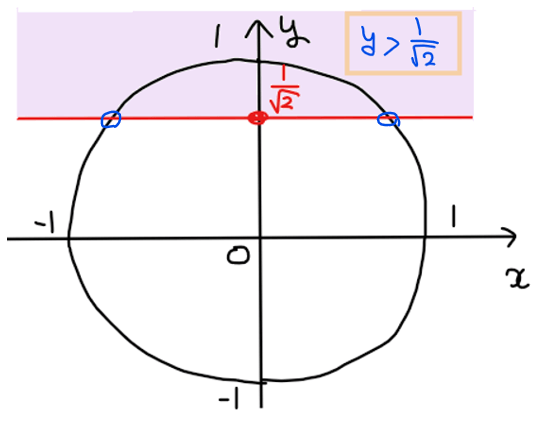
このとき、問題の不等号が、\(\small \displaystyle y\color{red}{>}\frac{1}{\sqrt{2}}\)と\(\small \displaystyle \frac{1}{\sqrt{2}}\)を含まない範囲のため、端点は白丸で表記しておく。
●補足
個人的には、三角方程式、不等式いずれの問題であっても単位円は必ずかくことをお勧めする。単位円を描くのを面倒くさがる人がいるが、単位円を描かないと頭の中で考えることが多くなり、かえって労力を使うことになる。2桁×2桁の掛け算は暗算するよりも筆算する方がミスなく速く解けるのと同じで三角関数を含む不等式の問題は単位円を描いて求める癖をつけておこう。
\(\small 0≦\theta<2\pi\)の範囲なので、\(\small \theta =0\)をスタート地点、\(\small \theta =2\pi\)をゴール地点としてSTEP1で図示した不等式の領域を通過する単位円上の部分を求める。
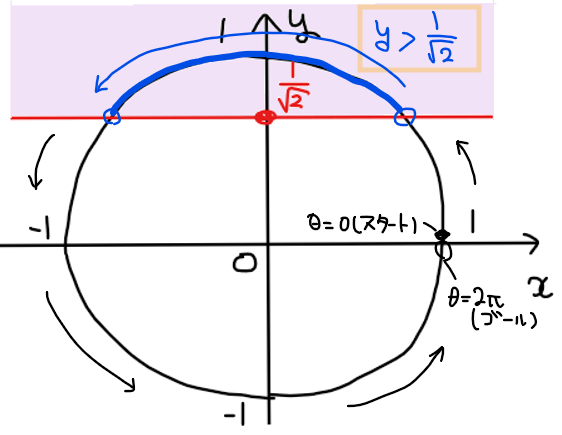
言い方を変えると求める範囲は必ず単位円の円周上の範囲になる。
※そもそも三角関数の成り立ちは、三角比を単位円を考えることで拡張させたものであるため
STEP2で求めた範囲の端点となる角度を求める。
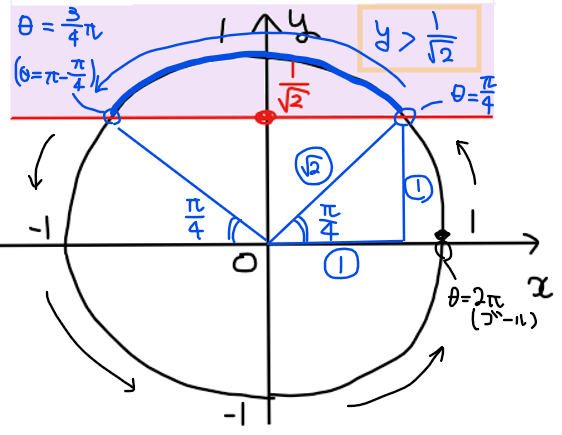
それぞれの端点での角度の求め方は三角方程式と同じ(詳細は、『単位円ってどう書くの?三角比の拡張(三角方程式)の解き方をsin、cos、tanごとに分かりやすく解説』で解説)。
よって、\(\small \displaystyle \frac{\pi}{4}<\theta<\frac{3}{4}\pi\)…【答】.
単位円と不等式\(\small \displaystyle y≧-\frac{1}{2}\)の範囲を図示すると以下の通り。
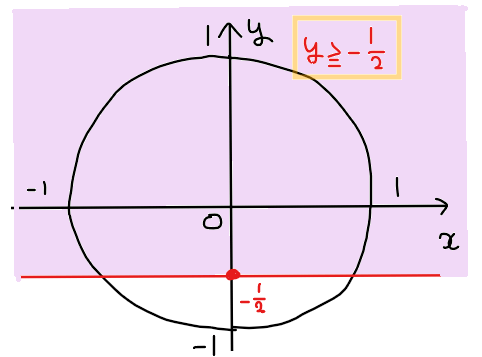
\(\small 0≦\theta <2\pi\)の範囲で、上図で図示した領域を通過するような角度の範囲を確認[*1]すると、下図の赤色部分と緑色部分の2箇所が該当する。
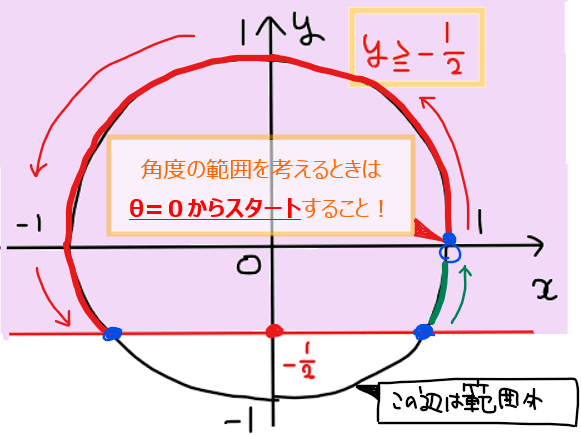
*1:【補足】よくあるミス…(-_-;)
不等式を満たす角度の範囲を下図のようにひとまとまりで考えてしまうと、最後に答えとなる角度の範囲を求めるときに、範囲の分かれ目が分かりにくくなる。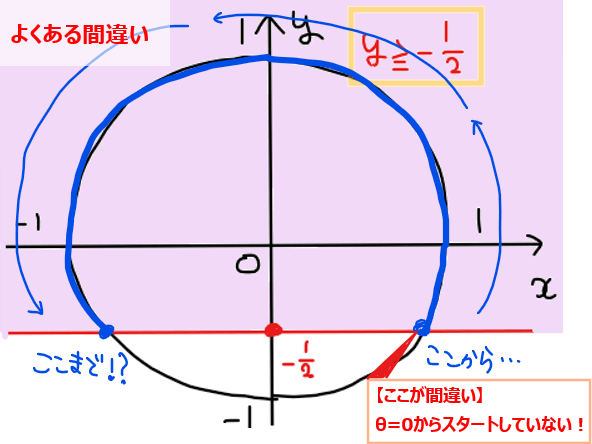
本問では\(\small 0≦\theta <2\pi\)という条件が課されているので、\(\small \theta =0\)からスタートし、\(\small \theta =2\pi\)まで単位円上を一周したときに不等式を満たす領域(紫色領域)を通過している部分を確認する必要がある。
最後に、赤色部分と緑色部分の角度の範囲を求めれば答えになる。
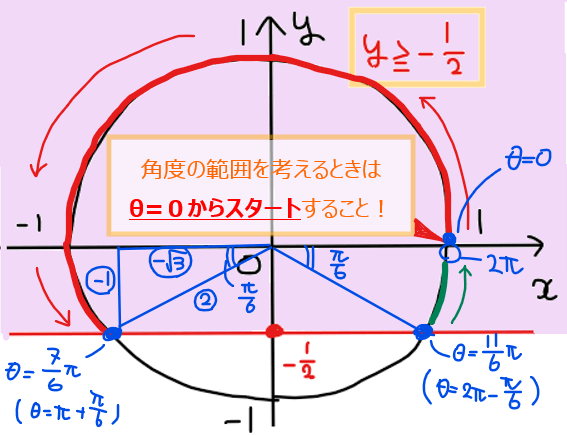
よって、\(\small \displaystyle 0≦\theta ≦\frac{7}{6}\pi, \space \frac{11}{6}\pi≦\theta <2\pi\)…【答】.
不等式\(\small \displaystyle y<-\frac{1}{2}\)の範囲を図示し、不等式を満たす角度の範囲を求めると下図の通り。
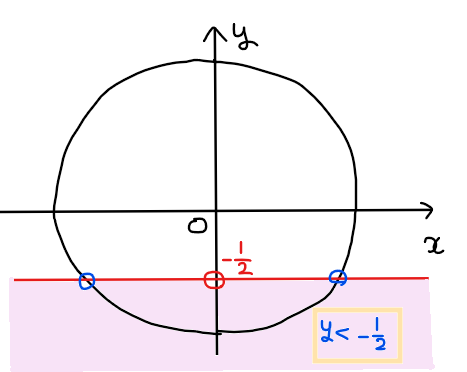
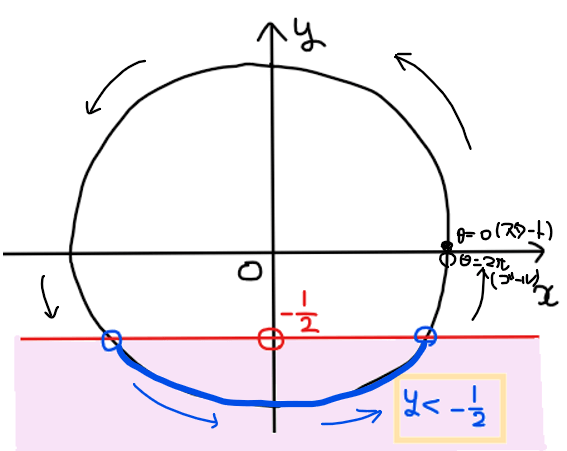
よって、青色部分を満たす角度の範囲は、\(\small \displaystyle \frac{7}{6}\pi<\theta<\frac{11}{6}\pi\)…【答】.
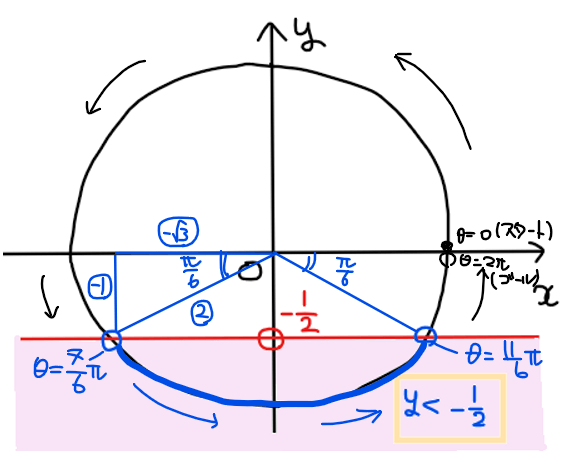
不等式\(\small \displaystyle y<\frac{\sqrt{3}}{2}\)の範囲を図示し、不等式を満たす角度の範囲を求めると下図の通り。
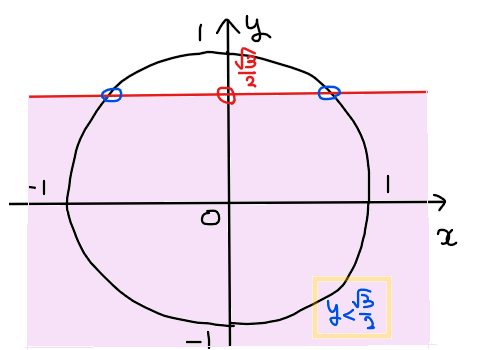
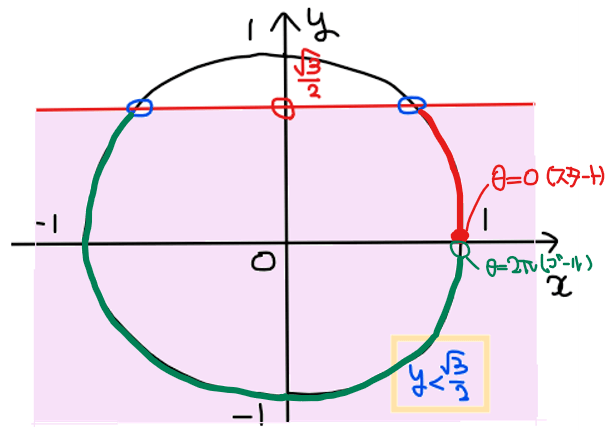
赤色部分と緑色部分の範囲に分かれるのでそれぞれの範囲の端点の角度を求めると下図のようになる。
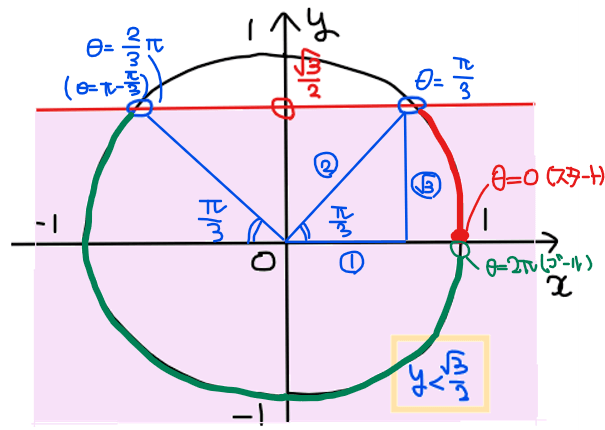
よって、求める答えは\(\small \displaystyle 0≦\theta<\frac{\pi}{3}, \space \frac{2}{3}\pi<\theta<2\pi\)…【答】.
●補足:問題と答えの不等号について
本問では\(\small \sin\theta <\sqrt{3}/2\)のように問題の不等号は「<」であるが、答えの不等号には、\(\small 0≦\theta <\pi/3, \cdots\)のようにイコール付きの不等号(≦)があり一致しないことに疑問を持つ人がいるが、2次不等式などと違って三角関数を含む不等式は問題の不等号と答えの不等号は必ずしも一致しないと考えてよい。なぜならば、問題の不等号は\(\small \sin\theta\)や\(\small \cos\theta\)の値の範囲を表しており、一方で答えの不等号は単位円上の角度 \(\small \theta\) の値の範囲を示しているので、両者は全く別物だからである。なので、答えとなる角度の範囲を求める際の不等号が「<」か「≦」かは、単位円を描いて丁寧に確認していく必要がある。
【問題2】\(\small \cos\theta\)に関する不等式の解き方(難易度:★★☆)
\(\small 0≦\theta < 2\pi\)のとき、次の不等式を解け。
(1)\(\small \displaystyle \cos\theta >\frac{1}{\sqrt{2}}\)
(2)\(\small \displaystyle \cos\theta ≦\frac{1}{2}\)
(3)\(\small \displaystyle \cos\theta >-\frac{1}{2}\)
(4)\(\small \displaystyle \cos\theta ≦-\frac{\sqrt{3}}{2}\)
\(\small \cos\theta\)に関する不等式なので、問題の不等式は \(\small \displaystyle x>\frac{1}{\sqrt{2}}\) であり、単位円上に図示すると下図のようになる。
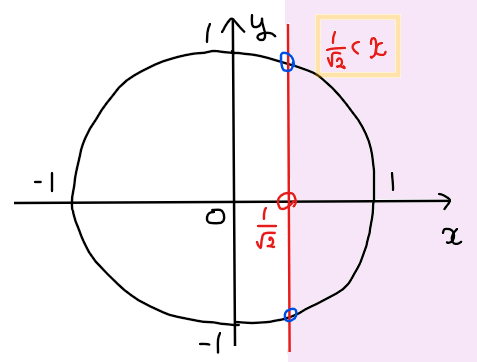
\(\small 0≦\theta <2\pi\)の範囲で、上図で図示した不等式の範囲を通過するような単位円上の部分を求めると、下図の赤色部分と緑色部分が該当する。
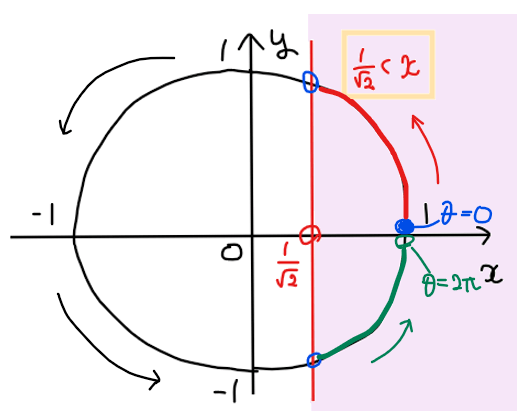
最後に、赤色部分と緑色部分の端点の角度を求めれば答えになる。
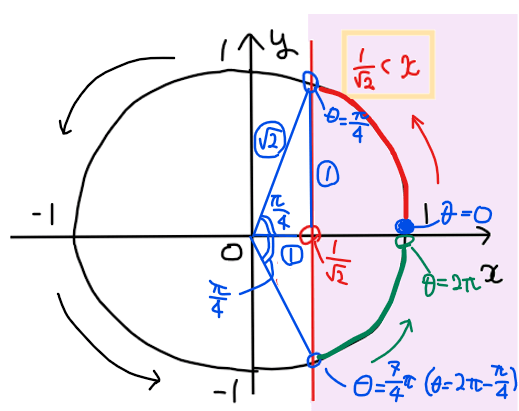
よって、\(\small \displaystyle 0≦\theta<\frac{\pi}{4}, \space \frac{7}{4}\pi<\theta<2\pi\)…【答】.
問題の不等式は \(\small \displaystyle x≦\frac{1}{2}\) なので、不等式を満たす単位円上の部分を図示すると下図の赤線部分になる。
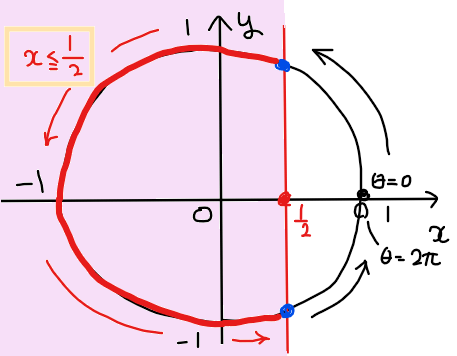
赤線部分の端点の角度を求めると下図のようになることから
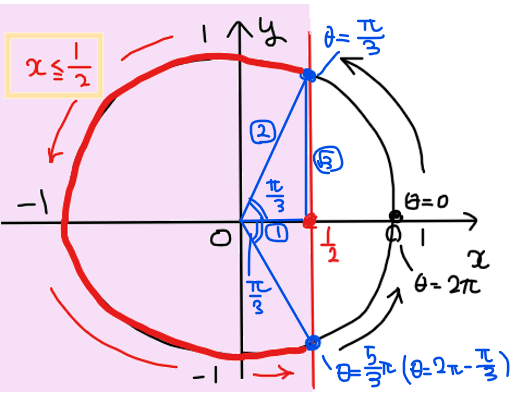
求める角度の範囲は、\(\small \displaystyle \frac{\pi}{3}≦\theta≦\frac{5}{3}\pi\)…【答】.
問題の不等式は \(\small \displaystyle x>-\frac{1}{2}\) なので、不等式を満たす単位円上の部分を図示すると下図の赤色部分と緑色部分になる。
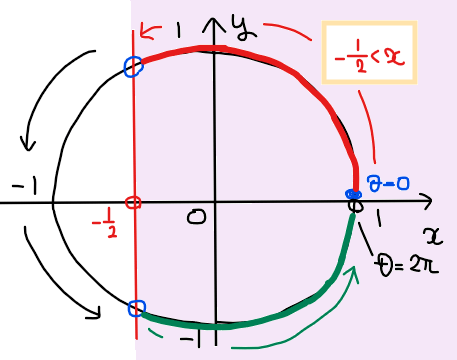
赤色部分と緑色部分の端点の角度を求めると下図のようになることから
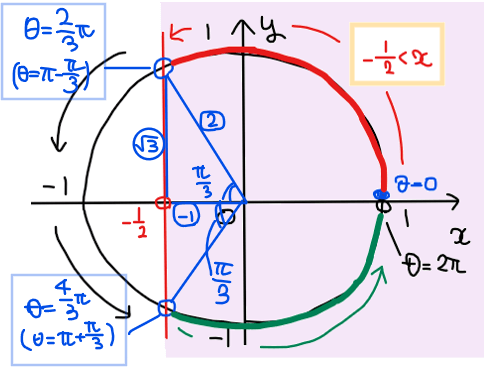
求める範囲は、\(\small \displaystyle 0≦\theta<\frac{2}{3}\pi, \space \frac{4}{3}\pi<\theta<2\pi\)…【答】.
問題の不等式は \(\small \displaystyle x≦-\frac{\sqrt{3}}{2}\) なので、不等式を満たす単位円上の部分を図示すると、下図の赤色部分になる。
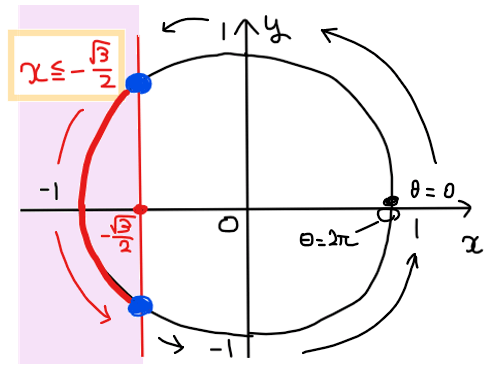
赤色部分の端点の角度を求めると下図のようになることから
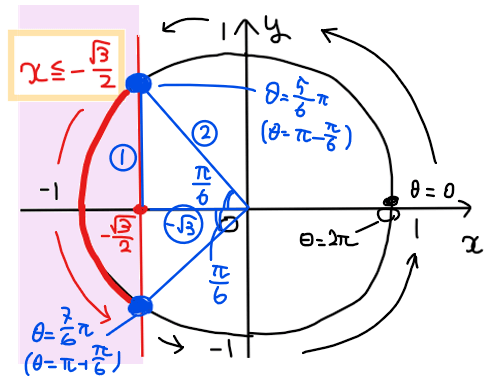
求める範囲は、\(\small \displaystyle \frac{5}{6}\pi≦\theta≦\frac{7}{6}\pi\)…【答】.
【問題3】\(\small \tan\theta\)に関する不等式の解き方(難易度:★★★)
\(\small 0≦\theta < 2\pi\)のとき、次の不等式を解け。
(1)\(\small \displaystyle \tan\theta ≧-\sqrt{3}\)
(2)\(\small \displaystyle \tan\theta ≧1\)
(3)\(\small \displaystyle \tan\theta <\sqrt{3}\)
(4)\(\small \displaystyle \tan\theta <-\frac{1}{\sqrt{3}}\)
\(\small \sin\theta\)や\(\small \cos\theta\)とは別物と考えて解く方が分かりやすい。
・単位円上の\(\small \tan\theta\)の値は下図のように考えることができる。
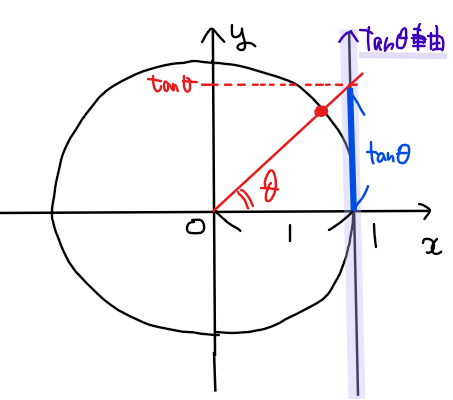
*単位円上の角度 \(\small \theta \) の延長線と直線 \(\small x=1\) との交点を考えると、
底辺が1なので高さがちょうど\(\small \tan\theta\)になるため。
・問題の不等式を直線 \(\small x=1\)(\(\small \tan\theta\)軸)上に図示し、
単位円上の該当範囲を求めていく考え方は\(\small \sin\theta\)や\(\small \cos\theta\)と同様。
まずは単位円をかき、\(\small \tan \theta =-\sqrt{3}\)が表す場所を確認していく。
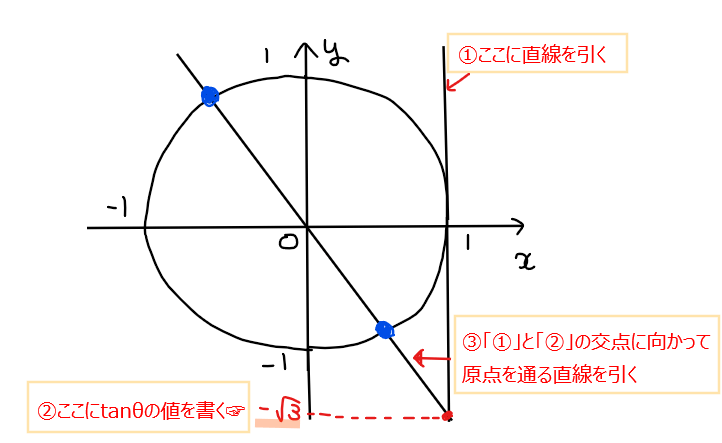
\(\small \sin\theta\)や\(\small \cos\theta\)は単位円の\(\small x、y\) 座標に対応していたのでわかりやすかったが、\(\small \tan\theta\)に対応する値の求め方は少々大変で、上図の①~③のステップで求めることになる…。
③で引いた直線と単位円との交点である青丸部分が\(\small \tan\theta=-\sqrt{3}\)の場所であり、この時の角度\(\small \theta\)がその解になる。
角度は最後に求めるとして、次は不等式が表す領域を図示することを考える(流れ自体は\(\small \sin\theta、\cos\theta\)の問題と同じ)。
\(\small -\sqrt{3}\)以上の範囲なので、\(\small \tan\theta\)の場合は下図の紫色斜線部分が不等式が表す領域になる(\(\small x=1\)の直線を\(\small \tan\theta\)軸みたいに考えると分かりやすいかも)。
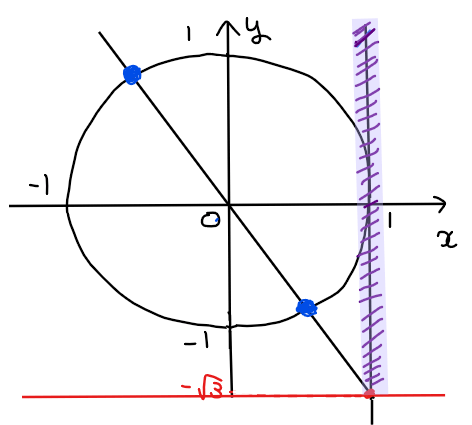
不等式の範囲がわかったら、今度は単位円上で不等式の範囲を満たす部分を考えることになるが、ここでも\(\small \tan\theta\)特有の注意点がある。それは、\(\small \tan\theta\)は\(\small \theta =\pi/2、3\pi/2\)が定義されていないため、必ず白丸になること。
この点に気を付けて範囲を求めると下図の青線部分、赤線部分、緑線部分が該当範囲となる[*1]。
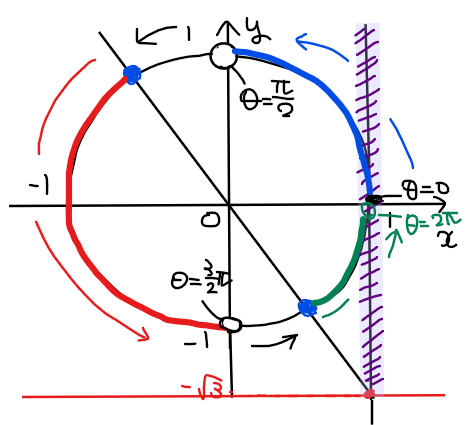
*1【補足】\(\small \tan\theta\)の範囲の求め方
\(\small \sin\theta\)や\(\small \cos\theta\)と違って直感的にわかりにくいので考え方を補足する。考え方としては大きくは変わらず、単位円上で不等式の範囲(紫色領域)を満たすか否かを \(\small \theta =0\)からスタートして確認していくことになる。
たとえば、下図の青色①箇所であれば、原点と結んだ直線(青点線)と直線 \(\small x=1\)が交わる部分が紫色領域内(=不等式の範囲内)になるため、条件を満たしていることが確認できる。
一方で、赤色②箇所は、原点と結んだ直線(赤点線)と直線 \(\small x=1\)が交わる部分が紫色領域の範囲外(=不等式の範囲外)になるため、条件を満たしていないことが分かる。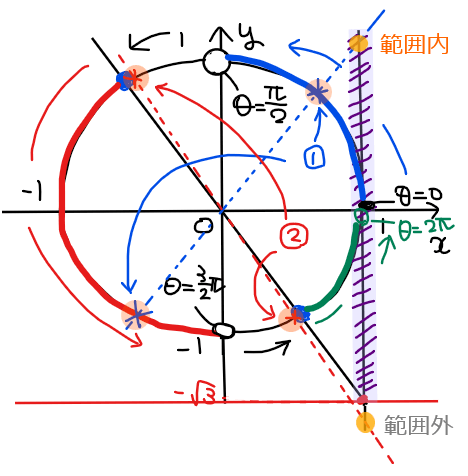
このように、単位円上の点と原点を結ぶ直線が直線 \(\small x=1\)とどこで交わるかを確認していくことで不等式を満たす点か否かが確認できる。
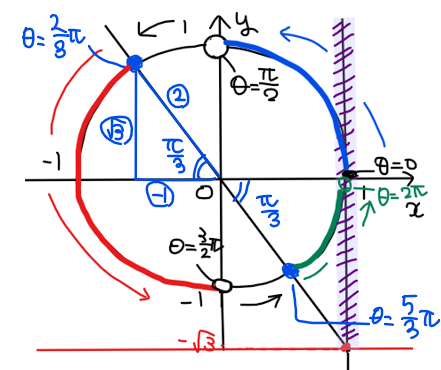
よって、求める範囲は、\(\small \displaystyle 0≦\theta<\frac{\pi}{2}\), \(\small \displaystyle \frac{2}{3}\pi≦\theta<\frac{3}{2}\pi\), \(\small \displaystyle \frac{5}{3}\pi≦\theta<2\pi\)…【答】.
まずは、単位円と\(\small \tan\theta≧1\)の範囲を図示する。
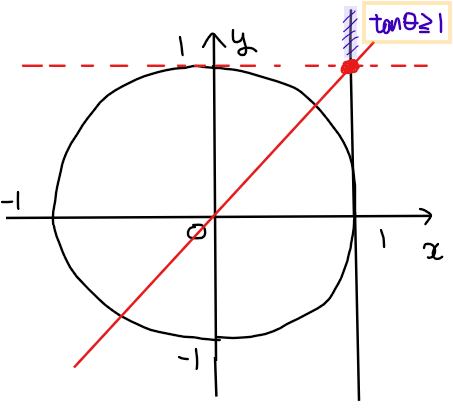
不等式の範囲(紫色範囲)を満たす単位円上の部分(単位円上の点と原点を結んだ直線 \(\small x=1\)との交点が紫色範囲に収まる部分)は下図の赤色部分と緑色部分の2箇所になる。
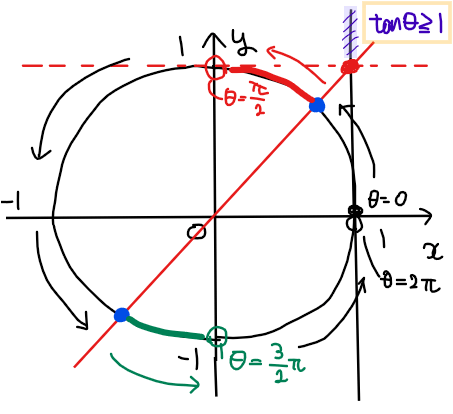
最後に、それぞれの範囲の端点の角度を求めると以下の通り。
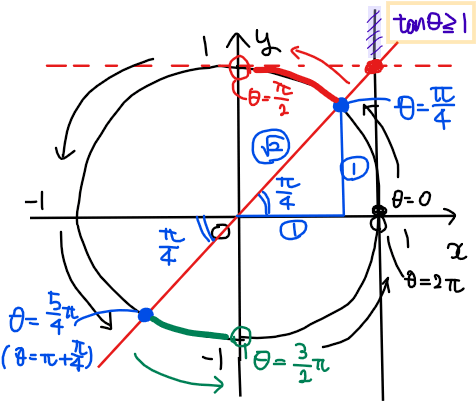
よって、求める範囲は、\(\small \displaystyle \frac{\pi}{4}≦\theta<\frac{\pi}{2}\), \(\small \displaystyle \frac{5}{4}\pi≦\theta<\frac{3}{2}\pi\)…【答】.
まずは、単位円と\(\small \tan\theta<\sqrt{3}\)の範囲を図示する。
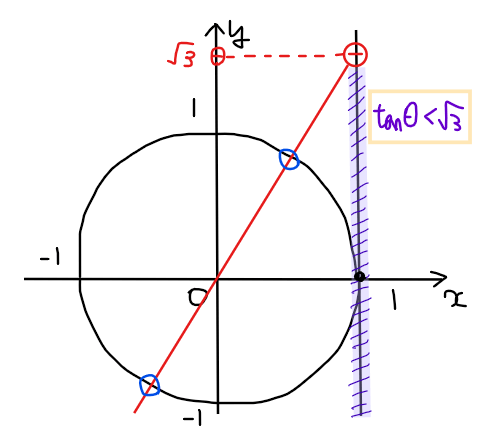
不等式の範囲(紫色範囲)を満たす単位円上の部分は下図の赤色部分と緑色部分、青色部分の3箇所になる。
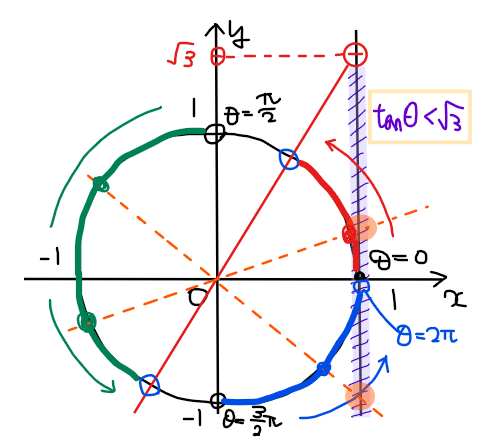
最後に、それぞれの範囲の端点の角度を求めれば答えが分かる。
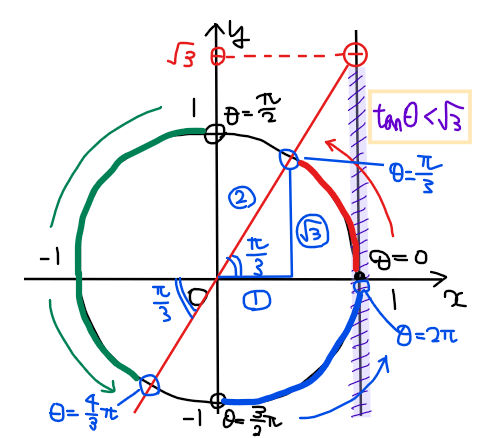
よって、\(\small \displaystyle 0≦\theta<\frac{\pi}{3}\), \(\small \displaystyle \frac{\pi}{2}<\theta<\frac{4}{3}\pi\), \(\small \displaystyle \frac{3}{2}\pi<\theta<2\pi\)…【答】.
単位円と\(\small \displaystyle \tan\theta <-\frac{1}{\sqrt{3}}\)の範囲を図示する。
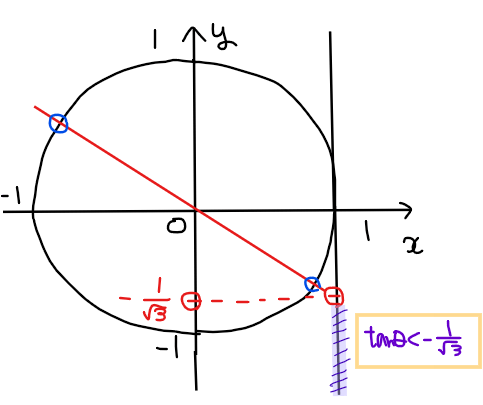
不等式の範囲(紫色範囲)を満たす単位円上の部分は下図の赤色部分と緑色部分の2箇所になる。
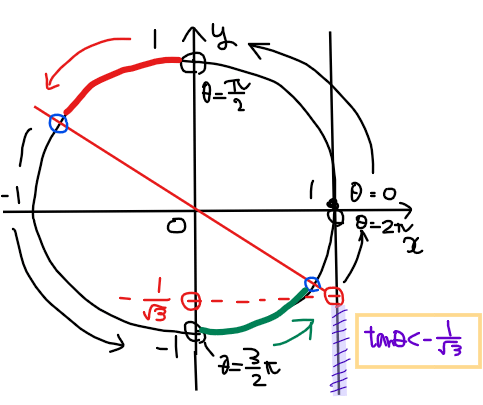
最後に、それぞれの範囲の端点の角度を求めれば答えが分かる。
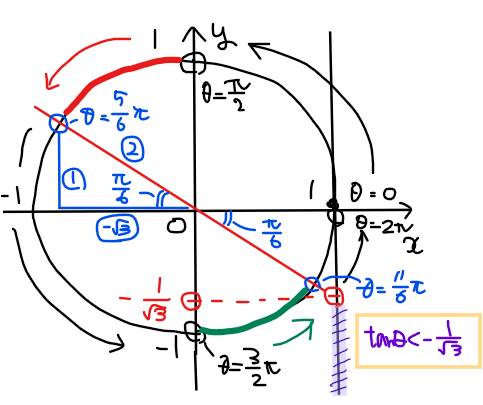
よって、\(\small \displaystyle \frac{\pi}{2}<\theta<\frac{5}{6}\pi\), \(\small \displaystyle \frac{3}{2}\pi<\theta<\frac{11}{6}\pi\)…【答】.
本記事のまとめ
今回は三角関数を含む不等式の解き方について、\(\small \sin\theta\)、\(\small \cos\theta\)、\(\small \tan\theta\)の3種類×各々4つのバリエーション=全12パターンをすべて解説してみました。
正直この12パターンが解けるようになれば、あとは単位円上の角度の値が異なる程度の違いなので三角関数を含む不等式の基本問題で解けない問題はなくなります。なので、しっかりと全パターン解けるようにしましょう。
いきなり全パターンは大変…という人は、まずは\(\small \sin\theta\)と\(\small \cos\theta\)をしっかり解けるようにしておきましょう(\(\small \tan\theta\)の不等式は入試ではそこまで出ないので優先度は落としてもよいと思います)。
また、解けない問題や苦手な問題があれば、それがあなたの苦手パターンということになるので、重点的に考え方を復習しておくとよいでしょう。
基本問題が完璧になったら、より実践的な問題にもチャレンジしてみましょう!
では、今回は以上です。お疲れさまでした!








コメント