今回は、非回転体の体積計算で頻出の不等式で表された立体の体積の求め方について、解説します。「共通部分の切り口の形ってどうやって把握すればいいの?」、「大学入試の受験対策でよく出てくるけど、解き方が全然わからない…」などの悩みを抱えた人向けに、考え方のコツや解き方の流れを分かりやすく解説しているので、ぜひ最後まで読んでみてください!
なお、本記事は、受験を意識した応用的なレベルになっているので、「積分を使った体積の基本問題について知りたい!」という人は、こちらの記事から読んでみることをお勧めします。
- 非回転体(不等式で表された立体)の体積の問題の解き方のコツが知りたい
- 共通部分の立体の形や断面の形を把握するコツが知りたい
- 実際の問題を通して自分が解けるのか確認したい
【はじめに】非回転体の体積とは?
今回のテーマである非回転体の体積って何なのかについて、はじめに簡単にお話しします。
高校で学習する積分を使って体積を求める問題は大きく2種類に分類できます。一つが「回転体の体積の問題」、もう一つが「非回転体の体積の問題」です。
回転体の体積の問題とは、関数や軸で囲まれた領域を\(\small x\)軸や\(\small y\)軸を基点に回転させたときにできる立体の体積を求める問題です。この分野は高校数学で体積の計算をするときの基本問題になっているので、多くの人が馴染みのある問題かなと思います。
一方で、非回転体の体積の問題とは、不等式で表された立体やいくつかの立体が重なる部分の体積を求める問題です。そのため、何かを軸にして回転させるというようなことがありません。このことから「非回転体」という名前で呼ばれることが多いです。
非回転体の体積の問題は、難関大学で頻出の問題となっており、レベルとしてはかなり上級者向けの分野になります。詳しくは大学の数学で学ぶ「重積分」という分野になりますが、高校ではその中でも簡単なものに限定して入試問題として出題されることが多いようです。
【解き方解説】非回転体の体積の求め方
ここからは、非回転体の体積の求め方について解説します。冒頭で上級者向けでレベルが高いと買いましたが、考え方の根幹は回転体の体積の問題で学んだことが活かせるので一緒に理解していきましょう。
【公式解説】非回転体の体積を求める公式
体積積分の公式とその意味
積分で体積が求められるのは、「(体積)=(微小体積の積み重ね)」という考え方があるからです。
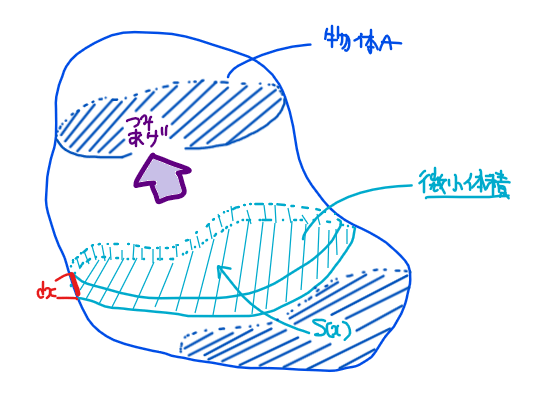
どういうことか、上図で説明します。厳密な証明ではありませんが、ここではイメージを掴むことを目的に説明していきます!
今、物体A(そら豆のような形)の体積を求めたいとします(形は何でもokです)。この物体Aを、とある断面で切ったときの断面積を\(\small S(x)\)(上図水色部分)とします。
次にその断面から微小な高さ \(\small \color{red}{dx}\)を考えます。すると、高さは微小(ほぼ0)なので、この立体は、底面積が\(\small S(x)\)、高さが\(\small \color{red}{dx}\)の円柱のような立体と考えることができます(底面が円じゃないので円柱ではないですが…)。

円柱のような立体の体積になります。
この微小体積を\(\small dV\)とします。もちろん、\(\small dV\)は底面積×高さで求まるので、\(\small dV=S(x)dx\cdots①\)です。
よって、求める物体Aの体積を\(\small V\)とすると、
$$V=\int dV$$
と表すことができます。「微小体積(\(\small =dV\))を積み重ねる(=積分する)と、全体の体積(\(\small =V\))になる」ということですね。これが冒頭に述べた「(体積)=(微小体積の積み重ね)」という考え方を数式化したものになります。
上記の式に、先程の①の関係式 \(\small dV=S(x)dx\)を代入すれば、一般に体積の積分公式は
$$V=\int S(x) dx$$
となります。
■非回転体の体積を求める公式
求める立体の断面積を\(\small S(t)\)として、\(\small t\)軸に沿って積み重ねる場合、その立体の体積\(\small V\)は、
$$\color{red}{V=\int S(t) dt}$$
※\(\small t\)軸(積分の軸)は、切り口の断面に垂直になるようにとる
【補足①】積分する軸の決め方
非回転体の公式では、一般的に積み重ねていく方向(積分の軸)を \(\small t\)軸としていますが、高校数学ではほとんどが、\(\small x、y、z\)軸のどれかになります。例えば、\(\small z\)軸方向に\(\small z=a~z=b\)まで積み上げる場合は、
$$V=\int_{\color{red}a}^{\color{red}b} S(\color{red}z) d\color{red}z$$
という感じです。
また、どの軸に沿って積分すればよいかは、「切り口の断面に垂直になるような軸に沿って積分」しましょう。このように設定することで積分計算がしやすくなります。

【補足②】回転体の公式との関係性
非回転体の公式は実は回転体の公式を一般化したものと考えることができます。どういうことかというと、回転体の体積の場合、断面積が必ず\(\small t\)軸を中心とした半径 \(\small R(t)\)の円となっているので、具体的に\(\small \color{red}{S(t)=\pi \{R(t)\}^2}\)と計算できてしまします。
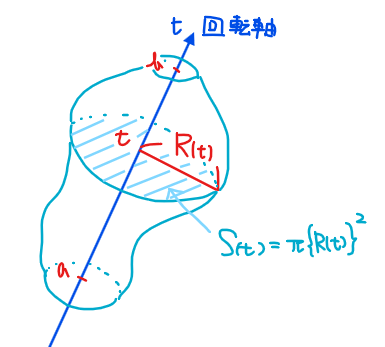
よって、非回転体の公式に代入することで\(\small V=\int_{a}^{b} \pi \{R(t)\}^2 dt\)となり、回転体の体積積分の時に紹介した公式と一致するわけです。詳細を知りたい人は、ぜひ「【積分】回転体の体積の求め方を徹底解説(x軸、y軸まわり、バームクーヘン型積分)」の記事を読んでみてください!
【解き方解説】非回転体の体積を求める手順
非回転体の体積(立体を表す領域の体積)の問題が苦手な人が問題を解く上でよく勘違いしている考え方があります。それが、次の2つです。
皆さんは大丈夫でしたか?多くの人がこれらの罠にはまっていしまう背景には、「立体の体積は形が分からないと求められないと思っているから」、「積分するためには断面積を計算する必要があるから」といった理由があると思います。
これらの意見は確かに正しいのですが、この方法で解こうとすると高度な「空間把握能力」が必要になってしまいます。でも、非回転体の体積の問題を解く上では、空間把握能力に頼らずに解く方法があります。結論、非回転体の体積計算は以下の手順で解くのがおすすめです。
■非回転体の体積の求め方
・STEP1:立体の領域を不等式で表す
・STEP2:切り口の断面を \(\small t\)の不等式で表す
・STEP3:切り口の断面を図示する
・STEP4:断面積を\(\small t\)で表す
・STEP5:非回転体の公式を使って体積を求める
ポイントは、図形だけに頼るのではなく図形を数式化して数学的に解いちゃえばいいわけです。
ちょっと手順が多いですが、実際の入試問題では誘導形式になっていることが多いので、そこまで難しくはないかなと思います。では、それぞれのステップについて、例題を通して具体的に解説していきます!
【例題で解説】非回転体の体積の求め方
\(\small xyz\)空間において、次の連立不等式が表す立体を考える。
$$\small 0≦x≦1,\space0≦y≦1,\space 0≦z≦1,\space x^2+y^2+z^2-2xy-1≧0$$
(1) この立体を平面\(\small z=t\)で切ったときの断面を\(\small xy\)平面に図示し、この断面の面積\(\small S(t)\)を求めよ。
(2) この立体の体積\(\small V\)を求めよ。
[北海道大]
この問題のように求める立体の領域が\(\small xyz\)空間上の不等式で表されている問題は、非回転体の体積を求める問題だと判断してokです。
では、ポイントの5ステップに沿って順番に解いていきましょう。
立体の領域を不等式で表す
今回は問題では、立体の領域はすでに問題文で書かれているのでこのステップは飛ばしてokです。問題によっては、「半径1の球体」といった言葉だけで立体が説明されていることもあるので、そういう場合は、立体の領域を不等式で表しておきましょう。
ちなみによく出てくる領域を表す不等式を載せておくので、参考にしてみてください。
■立体の領域を表す不等式
[1] 球体
原点を中心とした半径\(\small r\)の球体を表す領域は
$$x^2+y^2+z^2≦r^2$$

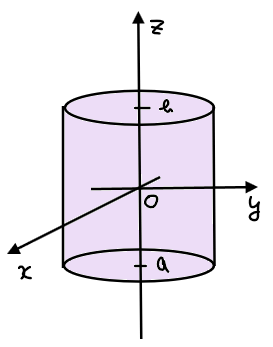
[2] 円柱
\(\small z\)軸を中心として、\(\small z=a \)から\(\small z=b\)まで伸びる半径\(\small r\)の円柱を表す領域は
$$x^2+y^2≦r^2,\space a≦z≦b$$
切り口の断面を \(\small t\)の不等式で表す
ここからがつまずく人が多い最初のポイント、「\(\small z=t\)での断面を図示する」です。「自分は空間把握能力がないから断面の形なんてわからない…」と思っている人に朗報です。空間把握能力がなくっても次のことをするだけで断面の形を把握することができるんです。それがSTEP2でかいた「切り口の断面を \(\small t\)の不等式で表す」です。
■断面の形の捉え方
立体の領域を表す不等式で\(\small z=t (※)\)を代入した不等式をもとに\(\small x,y,z\)の範囲を図示せよ!
※切り方によって適宜変えてください
では、実際にどういうことか解説していきます。
この問題で考えている立体の領域は
$$0≦x≦1,\space0≦y≦1,\space 0≦z≦1,\space x^2+y^2+z^2-2xy-1≧0$$
のすべて満たす立体で、\(\small 0≦x≦1,\space0≦y≦1\)は\(\small z\)を含まないのでそのまま、3つ目の不等式は、\(\small z=t\)として、\(\small 0≦ t ≦1\)です。最後は\(\small x^2+y^2+z^2-2xy-1≧0\)に\(\small z=t\)を代入して、\(\small x、y\)の値の範囲を考えてあげます。
\begin{equation}
\begin{split}
\color{blue}{x^2+y^2}+t^2\color{blue}{-2xy}-1&≧0\\
\color{blue}{(x-y)^2} &≧1-t^2\\
\end{split}
\end{equation}
ここで、\(\small 0≦t≦1\)より、\(\small 1-t^2≧0\)なので、
$$\color{red}{x-y≦-\sqrt{1-t^2},\quad \sqrt{1-t^2}≦x-y \quad \cdots①}$$
(補足)不等式の解き方
\(\small (x-y)^2 ≧1-t^2\)から①が導ける理由を補足しておきます。考え方としては、2次不等式の要領で\(\small \color{blue}{(x-y)^2} ≧ \color{red}{1-t^2}\)を左辺と右辺でそれぞれ関数だとみなして、グラフの位置関係から解いていきます。
左辺は\(\small (x-y)^2\)なので\(\small x-y\)を一つの変数とみなせば2次関数、右辺は\(\small 1-t^2\)で\(\small t\)は固定値なのでこれは定数関数です。また、\(\small 1-t^2≧0\)であることから、2次関数と定数関数の位置関係は下図のようになります。
よって、不等式の範囲、すなわち2次関数≧定数関数を満たすのは上図の緑斜線部分になるので、\(\small x-y\)の範囲としては、①の式の範囲になるわけです。
ちなみに、\(\small 1-t^2≧0\)であることをわざわざ述べているのは、もし仮に\(\small 1-t^2\)がマイナスの値であれば、下図のように常に2次関数の方が大きくなり、2次関数≧定数関数の不等式が常に成り立ってしまうことになりますが、今回はそうならないことを言っています。
\(\small 1-t^2<0\)だったらそもそも平方根の中身 \(\small \sqrt{1-t^2}\)が負になってしまうことになり数学的におかしくなるので、そうではないことを明示するためにも\(\small 1-t^2≧0\)であることは論証しておく方がベターだと思います。
\(\small -1≦x-y≦1\)と①の共通範囲を考えると、\(\small x-y\)の取り得る値の範囲は
$$-1≦x-y≦-\sqrt{1-t^2},\quad \sqrt{1-t^2}≦x-y≦1 \quad \cdots②$$
となります。
最後に、不等式の範囲を整理すると、
\begin{equation}
\begin{split}
0&≦x≦1\\
0&≦y≦1\\
0&≦t≦1\\
\color{red}{x+\sqrt{1-t^2}}&\color{red}{≦y≦x+1\quad \cdots③}\\
\color{blue}{x-1}&\color{blue}{≦y≦x-\sqrt{1-t^2} \quad \cdots④}\\
\end{split}
\end{equation}
③、④は図示しやすいように②の不等式を \(\small y\)について解いたものです。
切り口の断面を図示する
STEP2で求めた不等式を\(\small xy\)平面上に図示すると、下図の緑斜線部分(境界も含む)になります。
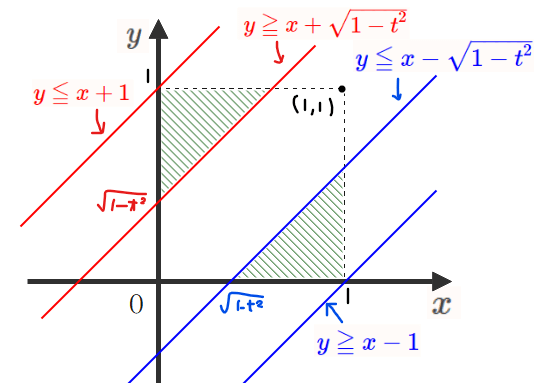
③は赤線の間、④は青線の間の範囲を表しているので
共通部分は緑線の部分になります。
これが\(\small z=t\)での切り口の断面図です…(1)の答え(図示部分)。
このように、不等式を使うことで断面の形を機械的に描くことができます。
断面積を\(\small t\)で表す
断面の形が把握できたら、断面積を \(\small t\)で表します。断面積は立体をどこで切るかによって変わるので\(\small t\)の関数として表せるということです。
今回の断面積は、直角三角形が2つですが、どちらも同じ三角形(一応、辺の長さを計算すると両方とも同じになるので合同ですね)なので片方の面積を計算して2倍すればよいでしょう。

右下の面積の方で計算すると、それぞれ辺の長さは上図の通りになるので、求める面積 \(\small S(t)\)は、
\begin{equation}
\begin{split}
S(t)&=\frac{1}{2}(1-\sqrt{1-t^2})^2 \times 2\\
&\color{red}{=(1-\sqrt{1-t^2})^2\quad \cdots ((1)の答え)}\\
\end{split}
\end{equation}
非回転体の公式を使って体積を求める
いよいよ最後のステップです。ここまで来たら、あとは断面積を積分して体積を求めるだけです。STEP3で\(\small 0≦t≦1\)と求めているので、非回転体の体積の公式 \(\small V=\int S(t) dt\)で積分範囲を\(\small 0≦t≦1\)、\(\small S(t)=(1-\sqrt{1-t^2})^2\)を代入して計算すると答えになります。
\begin{equation}
\begin{split}
V&=\int S(t) dt\\
&=\int_\color{red}0^\color{red}1 \color{red}{(1-\sqrt{1-t^2})^2} dt\\
&=\int_0^1 (1-2\sqrt{1-t^2}+(1-t^2)) dt\\
&=\int_0^1 (2-t^2) dt\\
&\quad -2 \color{blue}{\int_0^1 \sqrt{1-t^2} dt}\\
&=\bigg[2t-\frac{1}{3}t^3 \bigg]_0^1-2 \times \color{blue}{\frac{\pi}{4}}\\
&=\left(2-\frac{1}{3}\right) -\frac{\pi}{2}\\
&=\color{red}{\frac{5}{3}-\frac{\pi}{2} \quad \cdots ((2)の答え)}\\
\end{split}
\end{equation}
(補足)\(\small \displaystyle \int_0^1 \sqrt{1-t^2} dt\) の積分計算
この積分は\(\small t=\sin \theta\)として置換積分しても計算できますが、計算が大変です。一般に\(\small \displaystyle \color{red}{\int \sqrt{r^2-t^2} dt}\)の積分の形を見たら円を使って計算ができないか考えるようにしましょう!
今回みたいに積分範囲が0~\(\small r\)であれば1/4の円の面積、積分範囲が\(\small -r\)~\(\small r\)であれば1/2の円の面積になります。
この知識を使うと、今回の積分は半径が1の円の1/4の円の面積なので\(\small \displaystyle \frac{\pi}{4}\)と分かります。
【問題&解説】非回転体の体積の問題
【問題】円柱の共通部分の体積
\(\small xyz\)空間において、半径が1で\(\small x\)軸を中心軸として原点から両側に無限に伸びている円柱\(\small C_1\)と、半径が1で\(\small y\)軸を中心軸として原点から両側に無限に伸びている円柱\(\small C_2\)がある。\(\small C_1\)と\(\small C_2\)の共通部分のうち \(\small \displaystyle y≦\frac{1}{2}\)である部分を\(\small K\)とする。
(1) \(\small u\)を\(\small -1≦u≦1\)を満たす実数とするとき、平面\(\small z=u\)による\(\small K\)の切断面の面積を求めよ。
(2) \(\small K\)の体積を求めよ。
[東北大]
今回の問題では求める立体が不等式で表されていないので、まずは立体\(\small K\)を表す領域を不等式にする必要があります。
【徹底解説①】円柱の領域と立体 \(\small K\)を表す不等式
まずは、円柱\(\small C_1\)の領域を不等式で表してみましょう。\(\small x\)軸を中心として\(\small yz\)平面に平行な方向に半径1の円が広がるので、その領域は
$$\color{red}{y^2+z^2≦1 \quad \cdots①}$$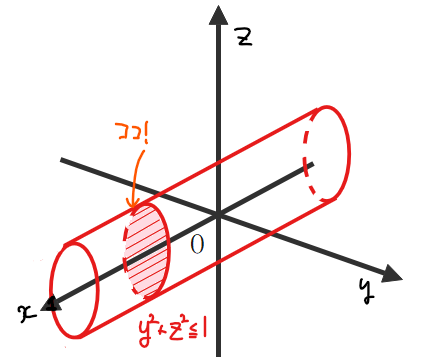

\(\small x\)軸は上図の奥から手前に伸びているイメージです。\(\small x\)軸方向は無限に伸びているので特に範囲はありません。
円柱\(\small C_2\)も同様に考えると\(\small xz\)平面に平行な方向に半径1の円が広がるので
$$\color{red}{x^2+z^2≦1 \quad \cdots②}$$
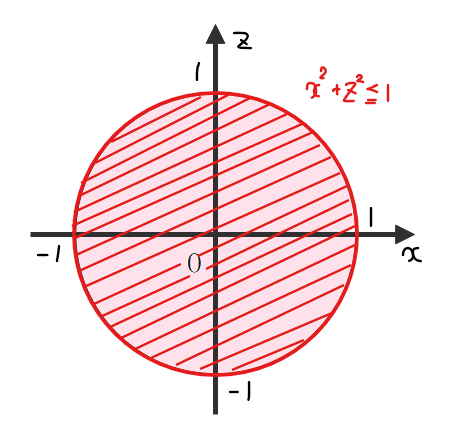
となります。
①、②と問題文から、求める立体\(\small K\)の領域を不等式で表すと
$$\color{red}{y^2+z^2≦1, \space x^2+z^2≦1, \space y≦\frac{1}{2}\quad \cdots(*)}$$
となります。
【徹底解説②】\(\small z=u\)での切り口を表す不等式と断面図
そうしたら、今度はSTEP2として、立体\(\small K\)を\(\small z=u\)で切ったときの断面の領域を\(\small u\)の不等式で表していきます。断面の形を考えるときには、解説パートでも紹介した通り、いきなり断面図を図示しようとするのではなく、不等式をもとに図示することを意識しましょう。
■断面の形の捉え方(再掲)
立体の領域を表す不等式で\(\small z=t (※)\)を代入した不等式をもとに\(\small x,y,z\)の範囲を図示せよ!
※切り方によって適宜変えてください
断面の領域は、\(\small (*)\)で\(\small z=u\)を代入すればよいので
$$y^2+\color{red}{u^2}≦1, \space x^2+\color{red}{u^2}≦1, \space y≦\frac{1}{2}$$
それぞれ解いていくと、\(\small -1≦u≦1\)なので\(\small 1-u^2≧0\)であることから
\begin{equation}
\begin{split}
&y^2+u^2≦1\\
&y^2≦1-u^2\\
-\sqrt{1-u^2}&≦y≦\sqrt{1-u^2}\\
\end{split}
\end{equation}
\(\small x^2+u^2≦1\)も同様に解くと\(\small -\sqrt{1-u^2}≦x≦\sqrt{1-u^2}\)となるので、\(\small (*)\)は
$$\color{red}{-\sqrt{1-u^2}≦x≦\sqrt{1-u^2}, \space -\sqrt{1-u^2}≦y≦\sqrt{1-u^2}, \space y≦\frac{1}{2}}$$
なんだか複雑な不等式ですが、\(\small u\)は固定値(たとえば\(\small u=1/2\)のような立体を切った場所の値)なので、例えば\(\small -\sqrt{1-u^2}≦x≦\sqrt{1-u^2}\)であれば、\(\small -1/2≦x≦1/2\)のようにただ\(\small x\)の値の範囲を示しているだけです(\(\small \sqrt{1-u^2}\)の形を見て無理関数だと思わないように注意)。
では、次は断面の領域を図示していきます。が、ここで1つ問題が出てきます。それは、\(\small y\)の値の範囲を表す不等式が、\(\small -\sqrt{1-u^2}≦y≦\sqrt{1-u^2},\space y≦\dfrac{1}{2}\)と2つあるので、両方の不等式を満たす共通範囲を求める必要がありますが、\(\small \sqrt{1-u^2}\) と \(\small \dfrac{1}{2}\)の大小関係が分からないので、共通範囲がはっきりしていないということです。
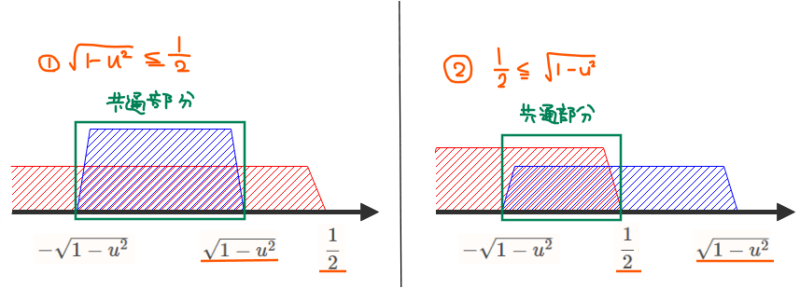
たとえば、上図の①のように\(\small \sqrt{1-u^2}≦\dfrac{1}{2}\)の場合、不等式の共通部分は\(\small \color{green}{-\sqrt{1-u^2}≦y≦\sqrt{1-u^2}}\)となります。一方で、②のように \(\small \dfrac{1}{2}≦\sqrt{1-u^2}\)の場合、共通部分は\(\small \color{green}{-\sqrt{1-u^2}≦y≦\dfrac{1}{2}}\)となります。
つまり、①か②かによって不等式の共通範囲が変わるので場合分けが必要ということになります。
①の場合、\(\small \sqrt{1-u^2}≦\dfrac{1}{2}\)を解くと、
\begin{equation}
\begin{split}
1-u^2&≦\frac{1}{4}\\
u^2&≧\frac{3}{4}\\
u≦-\frac{\sqrt{3}}{2},&\quad \frac{\sqrt{3}}{2}≦u\\
\end{split}
\end{equation}
もともと、\(\small u\)の取り得る値の範囲は\(\small -1≦u≦1\)なので、上記の不等式と合わせると
$$\color{red}{-1≦u≦-\frac{\sqrt{3}}{2},\quad \frac{\sqrt{3}}{2}≦u≦1}$$
②の場合も同様に \(\small \dfrac{1}{2}≦\sqrt{1-u^2}\)を解くことで、
$$\color{red}{-\frac{\sqrt{3}}{2}≦u≦\frac{\sqrt{3}}{2}}$$
これらの結果をまとめると、\(\small z=u\)での断面を表す不等式は以下の通りになります。
[1] \(\small \color{red}{-1≦u≦-\dfrac{\sqrt{3}}{2},\quad \dfrac{\sqrt{3}}{2}≦u≦1}\)のとき、
$$-\sqrt{1-u^2}≦x≦\sqrt{1-u^2}、\space -\sqrt{1-u^2}≦y≦\sqrt{1-u^2}$$
[2] \(\small \color{red}{-\dfrac{\sqrt{3}}{2}≦u≦\dfrac{\sqrt{3}}{2}}\)のとき、
$$-\sqrt{1-u^2}≦x≦\sqrt{1-u^2}、\space -\sqrt{1-u^2}≦y≦\dfrac{1}{2}$$
断面の領域はそれぞれ下図の赤線部分(境界線を含む)です。

(補足)断面の場合分けが必要な理由
今回のように\(\small u\)の値の範囲(つまり、\(\small z=u\)の切る場所)によって切り口の形が変わるのは立体 \(\small K\) に\(\small y≦\dfrac{1}{2}\)という条件があるからです。これは\(\small yz\)平面で見ると下図のようにかけた円の形になってるからです。[1]、[2]の断面図は下図の視点の方向から見た図ですね。
その影響で、\(\small -\dfrac{\sqrt{3}}{2}≦u≦\dfrac{\sqrt{3}}{2}\)の範囲では断面の形が[2]のような\(\small y=\dfrac{1}{2}\)固定になっているわけです。
【徹底解説③】断面積の計算
断面の形が分かったので断面積を計算します。断面の形を2パターンに場合分けしているので、断面積も各パターンごとに計算していきます。
[1] \(\small \color{red}{-1≦u≦-\dfrac{\sqrt{3}}{2},\quad \dfrac{\sqrt{3}}{2}≦u≦1}\)の場合
断面積は一辺が\(\small 2\sqrt{1-u^2}\)の正方形(軸の正と負のそれぞれの方向に\(\small \sqrt{1-u^2}\)なので注意)なので断面積を\(\small S(u)\)とおくと
$$S(u)=\left(2\sqrt{1-u^2} \right)^2=\color{red}{4(1-u^2)}$$
[2] \(\small \color{red}{-\dfrac{\sqrt{3}}{2}≦u≦\dfrac{\sqrt{3}}{2}}\)の場合
断面積は、縦が\(\small \dfrac{1}{2}+\sqrt{1-u^2}\)、横が\(\small 2\sqrt{1-u^2}\)の長方形なので
\begin{equation}
\begin{split}
S(u)&=\left(\frac{1}{2}+\sqrt{1-u^2}\right)\times(2\sqrt{1-u^2})\\
&=\color{red}{\sqrt{1-u^2}+2(1-u^2)}\\
\end{split}
\end{equation}
(解答)
\(\small \color{red}{-1≦u≦-\dfrac{\sqrt{3}}{2},\space \dfrac{\sqrt{3}}{2}≦u≦1}\)のとき、\(\small 4(1-u^2)\)、
\(\small \color{red}{-\dfrac{\sqrt{3}}{2}≦u≦\dfrac{\sqrt{3}}{2}}\)のとき、\(\small \sqrt{1-u^2}+2(1-u^2)\).
【徹底解説④】立体 \(\small K\) 体積の計算
\(\small z=u\)での断面積が分かったので、あとは、\(\small -1≦u≦1\)の範囲で積分してあげればokです。立式時のポイントは、先程求めた断面積\(\small S(u)\)の式が\(\small \dfrac{\sqrt{3}}{2}≦u≦1,\space -\dfrac{\sqrt{3}}{2}≦u≦\dfrac{\sqrt{3}}{2},\space -1≦u≦-\dfrac{\sqrt{3}}{2}\)の3区間でそれぞれ異なるので、積分もそれぞれの区間に分けてあげましょう。

積分範囲も各区間で分けて計算する必要あり
立体 \(\small K\)の体積を\(\small V\)とすると、非回転体の体積の公式から
\begin{equation}
\begin{split}
V&=\int_{-1}^1 S(u)du\\
&=\int_{-1}^{-\frac{\sqrt{3}}{2}} 4(1-u^2)du \quad \cdots \color{blue}{積分③}\\
&\quad +\int_{-\frac{\sqrt{3}}{2}}^{\frac{\sqrt{3}}{2}} \left( \sqrt{1-u^2}+2(1-u^2) \right)du \quad \cdots \color{blue}{積分②}\\
&\qquad +\int_{\frac{\sqrt{3}}{2}}^{1} 4(1-u^2)du \quad \cdots \color{blue}{積分①}\\
\end{split}
\end{equation}
このまま順番に計算していってもよいのですが、積分②は被積分関数が偶関数で積分範囲が対称になっているので
\begin{equation}
\begin{split}
積分②&=\int_{-\frac{\sqrt{3}}{2}}^{\frac{\sqrt{3}}{2}} \left( \sqrt{1-u^2}+2(1-u^2) \right)du\\
&=2\int_{0}^{\frac{\sqrt{3}}{2}} \left( \sqrt{1-u^2}+2(1-u^2) \right)du\\
&=2\int_{0}^{\frac{\sqrt{3}}{2}} \sqrt{1-u^2}du+4\int_{0}^{\frac{\sqrt{3}}{2}}(1-u^2) du\\
\end{split}
\end{equation}
ここで上式の第1項目は、下図のような円の面積になるので(詳細はここを参照)、

\begin{equation}
\begin{split}
&2\int_{0}^{\frac{\sqrt{3}}{2}} \sqrt{1-u^2}du\\
&=2\left(\color{blue}{\frac{60}{360}\times \pi}+\color{red}{\frac{1}{2}\times \frac{\sqrt{3}}{2} \times \frac{1}{2}}\right)\\
&=\frac{\pi}{3}+\frac{\sqrt{3}}{4}\\
\end{split}
\end{equation}
第2項目はそのまま計算すると、
\begin{equation}
\begin{split}
&4\int_{0}^{\frac{\sqrt{3}}{2}}(1-u^2) du\\
&=4 \bigg[ u-\frac{u^3}{3}\bigg]_{0}^{\frac{\sqrt{3}}{2}}\\
&=4\left(\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{8} -0\right)\\
&=\frac{3\sqrt{3}}{2}\\
\end{split}
\end{equation}
よって、積分②は \(\small \displaystyle \frac{\pi}{3}+\frac{7\sqrt{3}}{4} \cdots (★)\)
積分③は、\(\small t=-u\)と変数変換することで、積分範囲は、\(\small 1\)→\(\small \dfrac{\sqrt{3}}{2}\)、\(\small du=-dt\)となるので
\begin{equation}
\begin{split}
積分③&=\int_{1}^{\frac{\sqrt{3}}{2}} 4(1-(-t)^2)\cdot(-dt)\\
&=4 \int_{\frac{\sqrt{3}}{2}}^{1} (1-t^2)dt\\
&=積分①
\end{split}
\end{equation}
定積分では積分変数の違いは計算結果に関係ない(最後に値を代入してしまうため)ので、積分変数が \(\small t\)になっていますが積分①と積分③は同じということが分かります。
よって、
\begin{equation}
\begin{split}
積分①=積分③&=\int_{\frac{\sqrt{3}}{2}}^{1} 4(1-u^2)du\\
&=4 \bigg[ u-\frac{u^3}{3}\bigg]_{\frac{\sqrt{3}}{2}}^{1}\\
&=4\bigg[ \left( 1-\frac{1}{3}\right)-\left( \frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{8}\right) \bigg]\\
&=\frac{8}{3}-\frac{3\sqrt{3}}{2}\quad \cdots (★★)
\end{split}
\end{equation}
(★)、(★★)の結果から、\(\small \displaystyle V=\)積分①+積分②+積分③=積分①×2+積分②=\(\small \displaystyle 2 \left(\frac{8}{3}-\frac{3\sqrt{3}}{2} \right)+\frac{\pi}{3}+\frac{7\sqrt{3}}{4} =\frac{\pi}{3}+\frac{16}{3}-\frac{5\sqrt{3}}{4}=\color{red}{\frac{4\pi+64-15\sqrt{3}}{12} \quad \cdots(答)}\)
(解答)
$$\color{red}{\frac{4\pi+64-15\sqrt{3}}{12}}$$
本記事のまとめ
今回は不等式で表される立体の体積(非回転体の体積)の求め方について解説しました。ポイントをおさらいすると以下の通りです。
■非回転体の体積の求め方
・STEP1:立体の領域を不等式で表す
・STEP2:切り口の断面を \(\small t\)の不等式で表す
・STEP3:切り口の断面を図示する
・STEP4:断面積を\(\small t\)で表す
・STEP5:非回転体の公式を使って体積を求める
イメージしずらい立体の切り口の断面図を把握するときは、立体の形から断面を考えるのではなく、不等式をもとに図示することがポイントです。
■断面の形の捉え方
立体の領域を表す不等式で\(\small z=t (※)\)を代入した不等式をもとに\(\small x,y,z\)の範囲を図示せよ!
※切り方によって適宜変えてください
今回学んだ手順とポイントを使うことで、非回転体の問題は解くことができるので、しっかり復習しておきましょう。
では、今回はここまでです。お疲れさまでした!








コメント