今回は、合成関数の微分公式と証明方法、具体的な問題の解き方についてわかりやすく解説していきます。合成関数の微分を使う問題の見分け方が分からない人や、三角関数、分数関数、対数関数(log)を含んだ合成関数の微分の問題が苦手な人、逆に少し難しめの問題を解きたい人まで難易度別に問題を厳選しているので、ぜひ最後まで読んでみてください!
- 合成関数の微分ってどんな時に使えばいいのか分からない…
- 微分公式は覚えたんだけど、いざ問題を解こうとするとよく分からなくなってしまう…
- 合成関数の微分が不安なので、いろんなパターンの問題を解いて実力を確認したい!
- 少し応用的な微分の問題も解いてみたい!
- 合成関数の微分公式と証明をしっかりと理解したい!
【はじめに】合成関数の微分ってなに?
合成関数とは?
合成関数とは、一言でいうと「関数の中に関数が入った関数」です。言葉だけだとわかりにくいので合成関数の具体例で説明します。
■合成関数の具体例
【具体例①】
\(\qquad y=\sqrt{x^2+5}\)
【具体例②】
\(\qquad y=e^{\sin x}\)
①では、無理関数\(\small y=\sqrt{\color{red}z}\)という大きな関数があって、その\(\small \color{red}z\)の部分に、2次関数\(\small \color{red}z=\color{blue}{x^2+5}\)という関数が入り込んで関数\(\small y=\sqrt{\color{blue}{x^2+5}}\)になっています。②も同様で、\(\small y=e^{\color{red} z}\)という関数に\(\small \color{red} z=\sin x\)という関数が入り込んでいます。
このように、「関数の中に関数が入った関数」が合成関数です。
微分法の簡単なおさらい
高校で学ぶ微分にはいろいろな種類があり、それらをまとめて「微分法」といいます。もちろん、合成関数の微分は微分法の一種です。なので、「合成関数の微分ってなに?」と質問されたら、個人的には「関数の中に関数が入った関数の微分法のこと」って答えます。
言葉では理解していても、いざ問題になると「どの微分法で解けばいいんだ?」ってなってしまう人も多いんじゃないでしょうか?そんな人は、微分の種類が頭の中でごちゃごちゃになってしまっている状態だと思うので、まずは高校で学ぶ微分法の種類を把握することから始めましょう。
高校で学ぶ微分法は大きく分けると「関数単体の微分法」、「関数が組み合わさった微分法」、「特殊な関数の微分法」の3つです。他にも細かく分けるといろいろあるかもしれないですが、大きくはこの3つに分かれると思っておけば大丈夫だと思います。
①関数単体の微分法
多項式関数、三角関数、対数関数などの関数単体の微分公式です。最も基本的な微分法になります。
■多項式の微分公式
$$
\begin{equation}
\begin{split}
&(x^n)’=nx^{n-1}\quad \textrm{(\(\small n\)は実数の定数)}\\
\end{split}
\end{equation}
$$
■三角関数の微分公式
$$
\begin{equation}
\begin{split}
&(\sin x)’=\cos x\\
&(\cos x)’=-\sin x\\
&(\tan x)’=\frac{1}{\cos^2 x}\\
\end{split}
\end{equation}
$$
■対数関数の微分公式
$$
\begin{equation}
\begin{split}
&(\log_a |x|)’=\frac{1}{x\log a}\quad \textrm{(\(\small a>0\)かつ\(\small a\neq1\)の定数)}\\
\end{split}
\end{equation}
$$
■指数関数の微分公式
$$
\begin{equation}
\begin{split}
&(a^x)’=a^x\log a\quad \textrm{(\(\small a>0\)かつ\(\small a\neq1\)の定数)}\\
\end{split}
\end{equation}
$$
②関数が組み合わさった微分法
関数同士が組み合わさった場合の微分法です。「積の微分」や「商の微分」、「合成関数の微分」があります。
■積の微分法
→関数同士が掛け算されているときに使う
$$\{f(x)\cdot g(x)\}’=f'(x)g(x)+f(x)g'(x)$$
■商の微分法
→関数同士が割り算されているときに使う
$$\left(\frac{f(x)}{g(x)} \right)’=\frac{f'(x)g(x)-f(x)g'(x)}{\{g(x)\}^2}$$

今回解説する合成関数の微分法は、関数が組み合わさった場合の微分法の一種で、関数の中に関数が組み込まれているような場合に使うものなんだということを覚えておきましょう!
③特殊な関数の微分法
ここでは詳しく説明しませんが、媒介変数表示された関数の微分、陰関数の微分、逆関数の微分などがあります。
【公式/証明について】合成関数の微分公式と厳密な証明
合成関数の微分公式

合成関数の微分公式は、上記の公式で表されます。ただ、この公式だと\(\small f'(g(x))\)という部分がどんな微分しているのかが分かりにくいという問題があります。
そこで、どんな微分をしているのかをより詳しく書いた公式がこちら。
■合成関数の微分公式 ~詳しいver~
\(\small y=f(u)、u=g(x)\)とすると、合成関数 \(\small y=f(u)=f(g(x))\)の微分は
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$$
公式の意味と具体的な計算方法
合成関数の微分公式については正直、公式を覚えるよりも計算方法を覚える方が大事です。
では、具体例として\(\small y=(\sin x-2)^3\)の微分の計算方法を見ていきましょう。
関数 \(\small y=(\sin x-2)^3\)は、ざっくり見ると\(\small y=u^3\)という三次関数になっていて、\(\small u\)の中身に、三角関数 \(\small u=\sin x-2\)が組み込まれた合成関数になっています。
本題に戻って、\(\small y=(\sin x-2)^3\)の微分を計算していきます。合成関数の微分公式は、次のようなイメージで捉えるようにしましょう。
■合成関数の微分公式の意味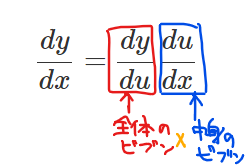
「合成関数の微分=(全体の微分)×(中身の微分)」である。
・全体の微分:ざっくりでみたときの関数の微分
→今回の例では、\(\small y=u^3\)の微分のこと
・中身の微分: \(\small u\)とおいていた部分の微分
→今回の例では、\(\small u=\sin x-2\)の微分のこと
実際に計算すると、
$$
\begin{equation}
\begin{split}
\frac{dy}{dx}&=(\color{red}{u^3})’\cdot(\color{blue}{\sin x-2})’\\
&=\color{red}{3u^2}\cdot \color{blue}{\cos x}\\
&=3(\sin x-2)^2 \cos x \quad \color{red}{←u=\sin x-2に戻すのを忘れない!}\\
\end{split}
\end{equation}
$$
合成関数の微分公式の証明方法
合成関数の微分公式の証明について解説します。ちょっと細かい話になるので、微分の問題が解ければいい!って人は飛ばして大丈夫です。
よく教科書に載っている証明は、感覚的にはわかりやすいですが、厳密にいうと不十分な証明になっています。
■教科書的証明
\(\small y=f(u)、u=g(x) \cdots①\)とし、\(\small x\)の増分を\(\small \Delta x\)、\(\small u\)の増分を\(\small \Delta u=g(x+\Delta x)-g(x) \cdots②\)とする。
合成関数\(\small y=f(g(x))\)の微分\(\small \dfrac{dy}{dx}\)は
$$
\begin{equation}
\begin{split}
\frac{dy}{dx}&=\lim_{\Delta x\to0}\frac{f(\color{red}{g(x+\Delta x)})-f(\color{blue}{g(x)})}{\Delta x}\\
&=\lim_{\Delta x\to0}\frac{f(\color{red}{u+\Delta u})-f(\color{blue}u)}{\Delta x}\\
\end{split}
\end{equation}
$$
ただし、青字部分は①、赤字部分は式②を利用。
\(\small \Delta x \to 0\)のとき、\(\small \Delta u \to 0\)になるので
$$
\begin{equation}
\begin{split}
(与式)&=\lim_{\Delta x\to0}\frac{f(u+\Delta u)-f(u)}{\Delta x}\\
&=\lim_{\Delta x\to0}\lim_{\Delta u\to0}\frac{f(u+\Delta u)-f(u)}{\color{red}{\Delta u}}\cdot\frac{\color{red}{\Delta u}}{\Delta x}\quad \cdots(★)\\
&=\lim_{\Delta u\to0}\frac{f(u+\Delta u)-f(u)}{\Delta u}\cdot \lim_{\Delta x\to0}\frac{g(x+\Delta x)-g(x)}{\Delta x}\\
&=f'(u)g'(x)\\
&=\frac{dy}{du}\frac{du}{dx}\\
\end{split}
\end{equation}
$$
この証明が不十分な理由は、途中(★)の部分で\(\small \Delta u\)を分母に割り込ませており、\(\small \Delta u =0\)の場合を考慮できていないからです。
\(\small \Delta u =0\)になるのはどんなときかというと、\(\small u=g(x)=c\)(\(\small c\)は定数)のような定数関数になっている場合や、微分しようとしている\(\small x\)付近で\(\small u=g(x)\)が一定になっている場合です。
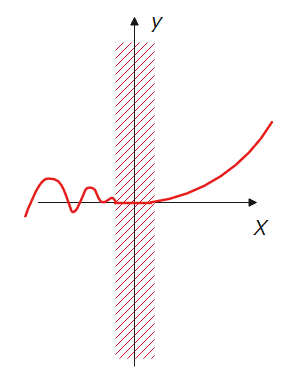
一定になっている
たとえば、上図のように\(\small x\)が赤斜線区間で一定で\(\small u=g(x)=c\)(\(\small c\)は定数)になっている関数があったとすると、赤線区間内の任意の2点\(\small x_1、x_2\)で、\(\small u_1=g(x_1)=c、u_2=g(x_2)=c\)が成り立つので、\(\small u\)の増分は\(\small \Delta u=u_2-u_1=c-c=0\)になります。
\(\small \Delta u=0\)の場合、すなわち合成関数に定数関数が含まれていることなんてまずないですから、このような例外的な場合を除けば教科書的証明で問題ないわけです。
でも、「教科書的証明だと\(\small \Delta =0\)の場合が考慮されてなくって、気持ち悪くて夜も眠れない!」という人向けに、以下に厳密バージョンの証明を解説します。
なお、この証明はこちらのサイトを参考にしています。説明がわかりやすいので併せて読んでみると理解が深まると思います。
■合成関数の微分公式の証明(厳密バージョン)
\(\small y=f(u)、u=g(x) \)とし、\(\small x\)の増分を\(\small \Delta x\)、\(\small u\)の増分を\(\small \Delta u=g(x+\Delta x)-g(x)\)、\(\small y\)の増分を\(\small \Delta y=f(u+\Delta u)-f(u)\)とする。
まず、以下のような関数を定義する。
$$\varepsilon_1=\frac{\Delta u}{\Delta x}-\frac{du}{dx}\quad \cdots①$$
この関数を図形的に解釈すると、第1項目が2点間の傾き(変化の割合)、第2項目が接線の傾きであり、その差分を表す関数が\(\small \varepsilon_1\)になっています。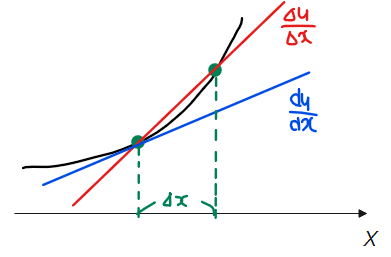
また、\(\small \varepsilon_1\)は
$$
\begin{equation}
\begin{split}
\lim_{\Delta x \to 0}\varepsilon_1 &= \lim_{\Delta x \to 0}\frac{\color{red}{\Delta u}}{\Delta x}-\frac{du}{dx}\\
&=\lim_{\Delta x \to 0}\frac{\color{red}{g(x+\Delta x)-g(x)}}{\Delta x}-\frac{du}{dx}\\
&=\frac{du}{dx}-\frac{du}{dx}\\
&=0
\end{split}
\end{equation}
$$
つまり、\(\small \Delta x \to 0\)で\(\small \varepsilon_1 \to 0 \cdots②\)。
次に、\(\small \varepsilon_2 \)を
$$
\varepsilon_2=
\begin{cases}
\dfrac{\Delta y}{\Delta u}-\dfrac{dy}{du} &(\Delta u \neq 0)\\
&\\
0& (\Delta u = 0)\\
\end{cases}
\quad \cdots③
$$
と定義します。
関数\(\small \varepsilon_2\)も式の意味自体は\(\small \varepsilon_1\)と同じです。たださっきと違うのは、\(\small \Delta u=0\)の場合、第1項目の\(\small \dfrac{\Delta y}{\Delta u}\)の分母が0になって式が破綻するので、それを回避するために\(\small \Delta u=0\)のときは関数\(\small \varepsilon_2 = 0\)としています。
\(\small \Delta u=0\)の定義の妥当性ですが、第1項目の\(\small \dfrac{\Delta y}{\Delta u}\)は2点間の傾きだったので、\(\small \Delta u =0\)、つまり定数関数の場合0です。第2項目の\(\small \dfrac{dy}{du}\)も\(\small y\)が定数関数ということは、\(\small y=f(u)=c\)のような定数なので、\(\small u\)で微分したら0になります。なので、0-0=0となることから、定義としても妥当だと判断できますね。
本題に戻って、\(\small \Delta u \neq 0\)の場合、③の定義から\(\small \lim\limits_{\Delta u \to 0} \varepsilon_2 = 0 \)。つまり、\(\small \Delta u \to 0\)で、\(\small \varepsilon_2 \to 0 \)。さらに、\(\small \lim\limits_{\Delta x \to 0} \Delta u =\lim\limits_{\Delta x \to 0} (g(x+\Delta x)-g(x))=0\)なので、\(\small \Delta x \to 0\)で\(\small \Delta u \to 0\)。よって、\(\small \Delta x \to 0\)で\(\small \varepsilon_2 \to 0 \cdots④\)。
\(\small \Delta y \)について、\(\small \Delta u \neq 0\)の場合、③より\(\small \Delta y=\left(\varepsilon_2+\dfrac{dy}{du}\right)\Delta u\)。一方、\(\small \Delta u = 0\)の場合、\(\small \Delta y=f(u+\Delta u)-f(u)=0\)。よって、\(\small \Delta u\)の値に関係なく、\(\small \Delta y\)は
$$\Delta y=\left(\varepsilon_2+\dfrac{dy}{du}\right)\Delta u \quad \cdots⑤$$
と書けます(⑤に\(\small \Delta u=0\)を代入すると\(\small \Delta y=0\)になる)。この式が今回の証明の肝になります。つまり、\(\small u\)が定数関数だろうが、普通の関数だろうが\(\small u\)の増分が0に近づけば(または0であれば)、\(\small y\)の増分も0に近づく(または0になる)ということです。
⑤と①より、\(\small \Delta y=\left(\varepsilon_2+\dfrac{dy}{du}\right)\color{blue}{\Delta u}=\left(\varepsilon_2+\dfrac{dy}{du}\right)\color{blue}{\left(\varepsilon_1+\dfrac{du}{dx}\right)\Delta x}\)となるので、合成関数の微分は
$$
\begin{equation}
\begin{split}
\frac{dy}{dx}&=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}\\
&=\lim_{\Delta x \to 0}\left(\varepsilon_2+\dfrac{dy}{du}\right)\left(\varepsilon_1+\dfrac{du}{dx}\right)\\
&=\color{red}{\lim_{\varepsilon_1 \to 0}\lim_{\varepsilon_2 \to 0}}\left(\varepsilon_2+\dfrac{dy}{du}\right)\left(\varepsilon_1+\dfrac{du}{dx}\right)\quad (∵ ②, ④)\\
&=\left(\color{red}0+\dfrac{dy}{du}\right)\left(\color{red}0+\dfrac{du}{dx}\right)\\
&=\dfrac{dy}{du}\dfrac{du}{dx}\\
\end{split}
\end{equation}
$$
この証明であれば、\(\small \Delta u=0\)と\(\small \Delta u\neq0\)をしっかり分けて議論するので分母が0になる気持ち悪さを解消できますね。
【問題/解説】合成関数の微分の問題と解き方
ここでは、合成関数の微分の計算方法について問題を通して解説します。
【初級編】基礎を固めたい人向けの問題4選
(1)\(\small y=\sqrt{3x^2+1}\)
(2)\(\small y=(\sin x+1)^2\)
(3)\(\small y=\log|\sin x+\cos x|\)
(4)\(\small y=2^{-x^3+x+1}\)
■合成関数の微分法
(合成関数の微分)=(全体の微分)×(中身の微分)
・ポイント①:全体の微分で微分する関数は、一番初めにぶち当たった関数のことが多い!
・ポイント②:全体の微分も中身の微分も、関数単体の微分のどれかになる!
ポイント①について補足すると、たとえば、関数\(\small y=(\sin^2 x-1)^3\)という合成関数があれば、「全体の微分」は一番初めにぶち当たる括弧の部分、\(\small y=\color{red}{(}\sin^2 x-1\color{red}{)^3}\)をみて、\(\small y=\color{red}{u^3}\)という3次関数の微分と考えればokです。すると、自動的に中身の関数は\(\small u=\sin^2 x-1\)になるわけです。
問題1:無理関数と多項式関数の合成関数の微分
(1)\(\small y=\sqrt{3x^2+1}\)
(1) 無理関数\(\small y=\sqrt{u}\)に2次関数\(\small u=3x^2+1\)が組み込まれた合成関数の微分と捉えると、
$$
\begin{equation}
\begin{split}
y’&=(\sqrt{u})’\cdot\color{blue}{(3x^2+1)’}\\
&=\color{red}{(u^{\frac{1}{2}})’}\cdot\color{blue}{6x}\\
&=\color{red}{\frac{1}{2}u^{-\frac{1}{2}}}\cdot 6x\\
&=\frac{1}{2\sqrt{u}}\cdot 6x\\
&=\color{red}{\frac{3x}{\sqrt{3x^2+1}}\quad \cdots(答)}\\
\end{split}
\end{equation}
$$
問題2:多項式関数と三角関数の合成関数の微分
(2)\(\small y=(\sin x+1)^2\)
(2) 2次関数\(\small y=u^2\)に三角関数\(\small u=\sin x+1\)が組み合わさった合成関数の微分と捉えると、
$$
\begin{equation}
\begin{split}
y’&=\color{red}{(u^2)’}\cdot \color{blue}{(\sin x+1)’}\\
&=\color{red}{2u}\cdot \color{blue}{\cos x}\\
&=\color{red}{2\cos x (\sin x+1)\quad \cdots(答)}\\
\end{split}
\end{equation}
$$
■補足
最後の答えは、括弧をはずして2倍角の公式を使うことで
$$y’=\color{red}{\sin 2x+2\cos x\quad \cdots(答)}$$
としてもokです。
問題3:対数関数と三角関数の合成関数の微分
(3)\(\small y=\log|\sin x+\cos x|\)
(3) 対数関数\(\small y=\log|u|\)に三角関数\(\small u=\sin x+\cos x\)が組み合わさった合成関数の微分と捉えると、
$$
\begin{equation}
\begin{split}
y’&=\color{red}{(\log|u|)’}\cdot\color{blue}{(\sin x+\cos x)’}\\
&=\color{red}{\frac{1}{u}}\cdot(\color{blue}{\cos x-\sin x})\\
&=\color{red}{\frac{\cos x-\sin x}{\sin x+\cos x}\quad \cdots(答)}\\
\end{split}
\end{equation}
$$
問題4:指数関数と多項式関数の合成関数の微分
(4)\(\small y=2^{-x^3+x+1}\)
(4) 指数関数\(\small y=2^u\)に3次関数\(\small u=-x^3+x+1\)が組み合わさった合成関数の微分と捉えると
$$
\begin{equation}
\begin{split}
y’&=\color{red}{(2^u)’}\cdot\color{blue}{(-x^3+x+1)’}\\
&=\color{red}{2^u\log 2}\cdot(\color{blue}{-3x^2+1})\\
&=\color{red}{\left \{(-3x^2+1)\log 2 \right \}2^{-x^3+x+1}\quad \cdots(答)}\\
\end{split}
\end{equation}
$$
【中級編】解けると差がつく問題2選
(1)\(\small y=\sin(\log(x^2+1))\)
(2)\(\small y=\sqrt[3]{x^2+2}\sin 2x\)
問題1:3つの関数が組み合わさった合成関数の微分
(1)\(\small y=\sin(\log(x^2+1))\)
3つ以上の関数が組み込まれた合成関数の微分も同様に
「全体の微分」×「中身の微分」で計算できる!
(合成関数の微分)=(全体の微分)×(中身の微分)×(中身の微分)×…
(1) 三角関数\(\small y=\sin u\)(全体の関数)と対数関数\(\small u=\log v\)(中身の関数1)、2次関数\(\small v=x^2+1 \)(中身の関数2)の3つの関数が組み合わさった合成関数の微分と捉えると、
$$
\begin{equation}
\begin{split}
y’&=\color{red}{(\sin u)’}\cdot\color{blue}{(\log v)’}\cdot\color{green}{(x^2+1)’}\\
y’&=\color{red}{\cos u}\cdot \color{blue}{\frac{1}{v}}\cdot \color{green}{2x}\\
&=\color{red}{ \frac{2x\cos (\log(x^2+1))}{x^2+1} \quad \cdots(答)}\\
\end{split}
\end{equation}
$$
問題2:合成関数の積の微分
(2)\(\small y=\sqrt[3]{x^2+2}\sin 2x\)
(2) 今回微分する関数は、\(\small \sqrt[3]{x^2+1}\)という合成関数と、\(\small \sin 2x\)という合成関数の2つが掛け算された関数と捉えることができます。
積の微分法を使うことで、
$$
\begin{equation}
\begin{split}
y’&=(\sqrt[3]{x^2+1}\cdot\sin 2x)’\\
&=\color{red}{(\sqrt[3]{x^2+1})’}\cdot\sin 2x+ \sqrt[3]{x^2+1}\cdot\color{blue}{(\sin 2x)’}\\
\end{split}
\end{equation}
$$
ここで、赤色部分の関数\(\small \sqrt[3]{x^2+1}\)を、\(\small v=\sqrt[3]{u}\)、\(\small u=x^2+1\)、青色部分の関数\(\small \sin 2x\)を、\(\small \color{blue}{w=\sin t}\)、\(\small \color{blue}{t=2x}\)の合成関数の微分と捉えることで
$$
\begin{equation}
\begin{split}
(与式)&=\color{red}{(u^{\frac{1}{3}})’\cdot(x^2+1)’}\cdot\sin 2x+ \sqrt[3]{x^2+1}\cdot\color{blue}{(\sin t)’\cdot(2x)’}\\
&=\color{red}{\frac{1}{3}u^{-\frac{2}{3}}\cdot 2x}\cdot\sin 2x+ \sqrt[3]{x^2+1}\cdot\color{blue}{\cos t \cdot 2}\\
&=\frac{2}{3}x\sin 2x(x^2+1)^{-\frac{2}{3}}+ 2\sqrt[3]{x^2+1}\cos 2x\\
&=\color{red}{\frac{2x\sin 2x}{3\sqrt[3]{(x^2+1)^2}}+ 2\sqrt[3]{x^2+1}\cos 2x \quad \cdots (答)}\\
\end{split}
\end{equation}
$$
【上級編】対数微分法
「関数の関数乗の微分」はlogをとってから微分せよ(対数微分法)。
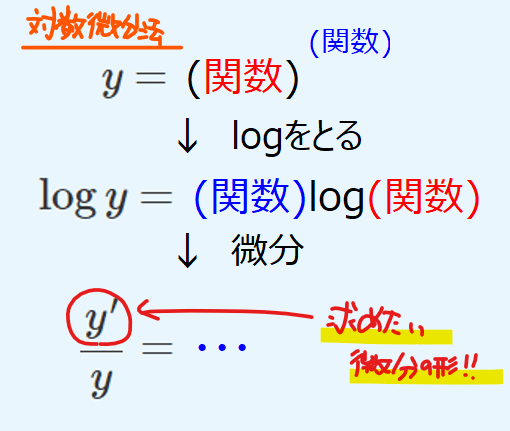
これまでと同様に\(\small y=x^u\)と\(\small u=\sin x\)の合成関数と考えて解こうとすると、\(\small (x^u)’\)の微分で躓きます。
「\(\small x^u\)の微分って、\(\small (x^u)’=ux^{u-1}\)じゃないの?(多項式の微分公式)」や、「指数関数の微分公式」が使えるんじゃない?」と思った人もいるかもしれません。そう思った人は公式をよーく見直してみてください。よく見ると\(\small n\)や\(\small a\)は定数じゃないとダメって書いてますね。なので、今回の問題みたいに、底も指数も関数の場合にはこれらの微分公式は使えないので注意してください!
では今回のように底も指数も関数の場合はどうするのかというと両辺のlogをとった関数を微分するとうまくいきます。このような微分法を「対数微分法」といいます。
では実際に計算してみます。まず\(\small y=x^{\sin x}\)の両辺のlogをとると
$$
\begin{equation}
\begin{split}
\log y &= \log (x^{\sin x})\\
\log y &= \sin x \log x \quad \cdots (*)\\
\end{split}
\end{equation}
$$
次に、この(*)の式の両辺を\(\small x\)で微分することを考えます。
右辺は積の微分法を使うことで
$$
\begin{equation}
\begin{split}
(右辺) &= (\sin x \log x)’\\
&= \color{red}{\cos x} \log x+\sin x \cdot \color{red}{\frac{1}{x}}\\
&= \cos x \log x+\frac{\sin x}{x}\quad \cdots①\\
\end{split}
\end{equation}
$$
左辺は、わかりやすくするために、あえて\(\small y=x^{\sin x}\)を代入して\(\small z=\log(x^{\sin x}) \)を\(\small x\)で微分すると考えます。すると、この微分は\(\small z=\log y\)という対数関数に、\(\small y=x^{\sin x}\)という関数が組み合わさった合成関数の微分と考えることができるので
$$
\begin{equation}
\begin{split}
(左辺) &= (\log y)’\cdot(x^{\sin x})’\\
&=\frac{1}{y}\cdot(x^{\sin x})’\\
&=\frac{(x^{\sin x})’}{x^{\sin x}} \quad \cdots②\\
\end{split}
\end{equation}
$$
式の中で出てきた\(\small (x^{\sin x})’\)が今回求めたかった微分なので、①と②から
$$
\begin{equation}
\begin{split}
\frac{(x^{\sin x})’}{x^{\sin x}}&=\cos x \log x+\frac{\sin x}{x}\\
(x^{\sin x})’&=\color{red}{\left(\cos x \log x+\frac{\sin x}{x}\right)x^{\sin x}\quad \cdots (答)}\\
\end{split}
\end{equation}
$$
【まとめ】合成関数の微分法について
今回は、合成関数の微分について問題ごとに解き方を解説してきました。
■合成関数の微分法
(合成関数の微分)=(全体の微分)×(中身の微分)
・ポイント①:全体の微分で微分する関数は、一番初めにぶち当たった関数のことが多い!
・ポイント②:全体の微分も中身の微分も、関数単体の微分のどれかになる!
合成関数の微分公式自体を覚えるのではなく、上記のようなイメージを掴んで、最終的には関数単体の微分、すなわち、多項式関数(\(\small x^n、\sqrt{x}\)など)、三角関数(\(\small \sin x\)など)、対数関数(log)、指数関数(\(\small a^x\))の微分で解けるという流れが掴めたんじゃないかなと思います。
微分の問題自体はここでは紹介しきれないほどたくさんの問題があるので、そのあたりは問題集にお任せするとして、いろいろな問題を解く際に躓いたら、またこの記事を見返してもらって解き方を振り返るときに活用してもらえたらと思います。
それでは本日はここまでです。お疲れさまでした!






コメント