今回は、通過領域を図示する問題について解説していきます。「解き方の方針が分からない…」、「解答を読んだときは分かったつもりでも、自力で解こうとすると分からなくなる…」といった悩みを抱えている人は多いと思います。また、少し勉強したことがある人であればファクシミリ法(ファクシミリ論法)や順像法、逆像法、包絡線などの言葉を聞いたことがある人もいるかもしれません。でも、「実はそれぞれがどんな解き方なのかよくわかってない…」という人は多いと思います。
本記事ではこれらの悩みに対して実際の問題を通して基本的な考え方やおすすめの解き方について解説しているので、ぜひ最後まで読んでみてください!
- 解き方の方針を知りたい(何からどうやって解けばいいの?)
- 各種解き方(順像法、逆像法、包絡線など)の考え方を知りたい
- おすすめの解き方を教えてほしい!
- 通過領域の問題を解いて実力チェックをしたい
【基礎知識】通過領域を図示する方法3選
通過領域を図示する方法は大きく3種類あります。まずは、それぞれの考え方を理解しましょう。
【解法1】順像法(ファクシミリ法)
通過領域をとある\(\small x\)で切断して\(\small y\)座標の取り得る範囲を求めることで通過領域を図示する方法です。1回1回\(\small x\)の値を固定して考える手法がファックスの原理に似ているため、「ファクシミリ法」や「ファクシミリ論法」とも呼ばれます。ファックスのことはよくわからないので、個人的には「縦切りスライス法」の方が分かりやすいとか思っています(余談です…)。
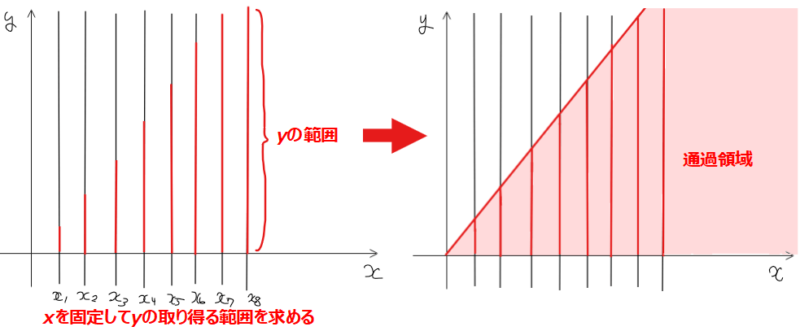
\(\small x=x_1、x_2、\cdots\)のそれぞれで\(\small y\)座標の取り得る値の範囲を求めておき
最後にその範囲を足し合わせたものが通過領域になるという考え方
3つの方法の中で最も一般的に利用されています。
【解法2】逆像法
順像があれば逆像があるということで、2つ目の解き方は「逆像法」です。
とある点\(\small (x,y)\)に対して、方程式を満たす解が存在するための条件から逆に点\(\small (x,y)\)の範囲を求めることで通過領域を図示する方法です。言葉だけだと何を言っているのかさっぱりわからないと思うので、具体的な考え方はこの後の例題で一緒に理解していきましょう。
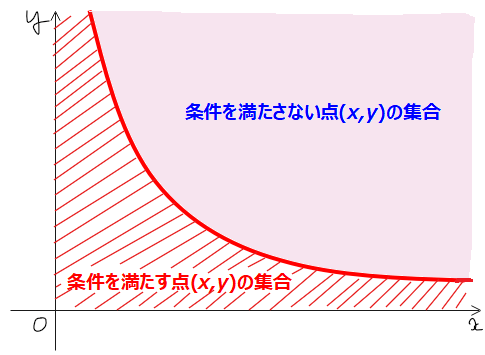
条件式(方程式)が解を持つ条件から点\(\small (x,y)\)の
存在範囲を求めることで通過領域を求める方法。
【解法3】包絡線の利用
包絡線とは一言でいうと「すべての接線によって作り出される曲線」のことです。文字より図で見た方が分かりやすいと思います(下図)。
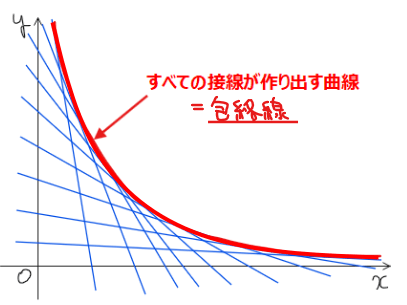
接線(青色)によって作り出される曲線が包絡線(赤色)。
通過領域を求める最後の方法は、この包絡線を求めることで通過領域を図示するという解き方です。変数の値に応じて直線をずらすことで通過領域を求めていくイメージです。
包絡線を数学的に求める方法自体は大学の偏微分の知識が必要になるので、この解法は理解するというよりは、こんな解き方もあるんだなぁ程度でいいかなと思います。
【徹底解説】通過領域の求め方
では実際の問題を通してそれぞれの解法での解き方を解説していきます。
実数\(\small t\)が正の値をとるとき、直線\(\small 2tx+y+t^2=0\)が通る領域を図示せよ。
順像法による解き方
■順像法の解法手順
・STEP1:\(\small x=k\)で切断したときの\(\small y\) 座標の値を求める … \(\small x\)固定
・STEP2:\(\small y\)座標の最大値、最小値を\(\small k\)の式で求める … \(\small y\)の範囲
・STEP3:STEP2の式を\(\small xy\) 平面上に図示する … 範囲の足し合わせ
\(\small x=k\) (固定)で切断したときの\(\small y\) 座標の値を求める
直線\(\small 2tx+y+t^2=0\)が通る領域を直線\(\small x=k\)(固定)で切断します。そのときの\(\small y\)座標は、
\begin{split}
2t\color{red}{k}&+y+t^2=0\\
\Rightarrow \space y&= -2kt-t^2
\end{split}
と求まります。
(補足)\(\small x=k\)(固定)とは?
\(\small k\)固定とは、とある値\(\small k\)を考えるということ。具体的には例えば\(\small x=2\)で切ったと考えるということです。すると、そのときの直線の式は
\begin{split}
4t&+y+4=0\\
\Rightarrow \space y&= -4t-4
\end{split}
となります。
あとは、\(\small t>0\)の範囲で\(\small y= -2kt-t^2\)が取り得る値の最大、最小を求めることで、\(\small x=k\)で切断したときの\(\small y\)座標の値の範囲が分かります。
\(\small y\)座標の最大値、最小値を\(\small k\)の式で求める
\(\small t>0\)の範囲で、変数\(\small t\)の2次関数\(\small y= -t^2-2kt\)の最大値、最小値を求めます。このときに、式中の\(\small k\)は定数であることに注意します(\(\small x=k\)(固定)なので)。
2次関数のグラフは、軸が\(\small t=-k\)で頂点の座標が\(\small (-k、k^2)\)、\(\small t\)軸とは\(\small t=0、-2k\)で交わるグラフであることが分かります。
たとえば、以下のような図であれば\(\small y\)の最大、最小はこんな感じになります。
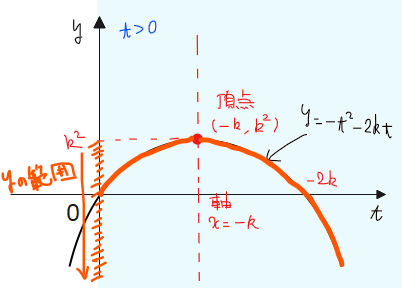
\(\small y\)の最大値、最小値は2次関数\(\small y= -t^2-2kt\)の位置によって大きく変わるので、軸の位置で場合分けして考えます。
[1]軸 \(\small t=-k\)が負、すなわち、\(\small k>0\)の場合
軸が負の範囲にあることから、グラフは下図のようになるので、\(\small \color{blue}{t>0}\)での2次関数\(\small y= -t^2-2kt\)の最大値は0、最小値はなし(\(\small -\infty\))なので、\(\small \color{red}{y<0\cdots①}\).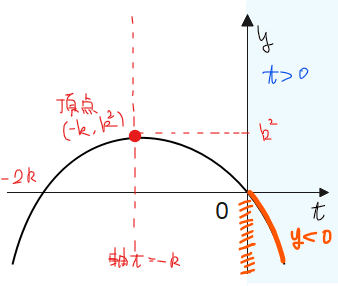
[2]軸 \(\small t=-k\)が正、すなわち、\(\small k<0\)の場合
軸が正の範囲にあることから、グラフは下図のようになるので、\(\small \color{blue}{t>0}\)での2次関数\(\small y= -t^2-2kt\)は頂点部分で最大となり、最大値は \(\small k^2\)、最小値はなし(\(\small -\infty\))なので、\(\small \color{red}{y≦k^2\cdots②}\).
[3]軸 \(\small t=-k\)が0、すなわち、\(\small k=0\)の場合
考えるグラフは\(\small \color{red}{y=-t^2}\)になるので、下図のグラフから、\(\small \color{blue}{t>0}\)での最大値は0、最小値はなしとなり、\(\small \color{red}{y<0\cdots③}\)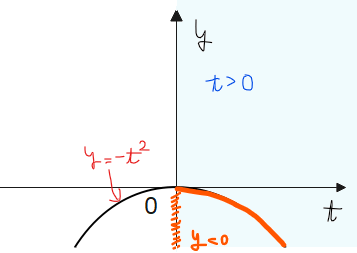
STEP2の式を\(\small xy\) 平面上に図示する
最後は求めた結果①、②、③を\(\small xy\) 平面上に図示すれば完了です。②は\(\small k\)の式になっていますが、もともと\(\small k\)は\(\small x=k\) (固定)という「とある\(\small x\)の値」だったので、様々な\(\small k\)の値を集めるとそれは変数 \(\small x\)を考えることと同じなので、②は\(\small y≦x^2\)と考えることができます。
よって、図示する不等式の範囲は
\begin{cases}
x<0\mathbf{のとき、} \space y≦x^2 \color{blue}{\cdots ②}\\
x=0\mathbf{のとき、} \space y<0 \color{blue}{\cdots ③}\\
x>0\mathbf{のとき、} \space y<0 \color{blue}{\cdots ①}\\
\end{cases}
となるので、通過領域は下図の通り。ただし、\(\small y=x^2\)との境界を含み、\(\small x\)軸0以上の部分(赤線箇所)は含まない。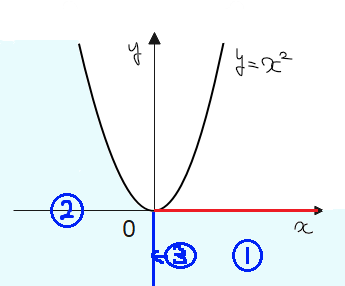 …(答)
…(答)
逆像法による解き方
■逆像法の解法手順
・STEP1:\(\small x、y\)を固定し条件式を変数の方程式に変形
・STEP2:方程式が解を持つための条件を求める
・STEP3:条件の不等式を図示する
\(\small x、y\)を固定し条件式を変数の方程式に変形
\(\small x、y\)を固定して(\(\small x、y\)は定数だと思って)、問題文の直線\(\small 2tx+y+t^2=0\)を変数\(\small t\) の2次方程式とみなします。つまり
$$ t^2+2xt+y=0$$
のように式変形しておきます。
方程式が解を持つための条件を求める
STEP1で求めた方程式は、\(\small t>0\)の実数の値をとるので、逆に考えれば、
\(\small t>0\)で2次方程式 \(\small t^2+2xt+y=0\)が実数解を持つ
ということです。つまり、考えるべき問題を、上記の条件を満たす2次方程式の解の存在範囲求める問題に帰着させることができたわけです。2次方程式の解の存在範囲の求め方の詳細については、「2次方程式の解の存在範囲」の記事にお任せするとして、判別式、軸、境界条件(\(\small y\)切片)の観点で考えていけばいいんでしたね。
ひとまず、軸が\(\small t=-x\)、切片が\(\small y\)なので、解を持つような図を描いてみるとこんなパターンが考えられそうです。
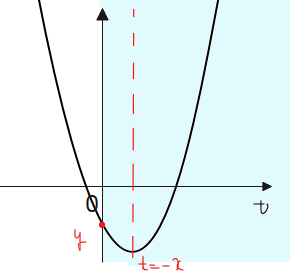
■軸(\(\small t=-x\))が負、すなわち\(\small x>0\)の場合
\(\small t>0\)の範囲に実数解を持つためには、切片が負、つまり \(\small y<0\)が条件…①。
※判別式 \(\small D≧0\)も条件になるが、切片が負であれば必ず実数解を1つ以上持つのであえて考えなくてもOK
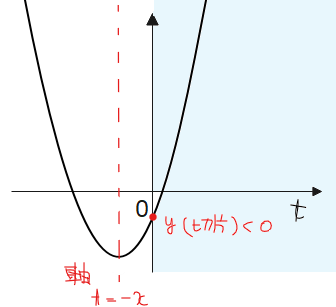
■軸(\(\small t=-x\))が正、すなわち\(\small x<0\)の場合
\(\small -x>0\)、すなわち \(\small x<0\)。下図を見るとわかるように、軸が正の場合は、切片は正でも負でも実数解を持つようなパターンがあるので、今回は切片の条件はありません。
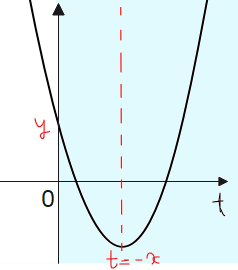
判別式については、実数解を1つ以上は持つ必要があるので、\(\small D≧0\)が条件となります。
よって、
\begin{split}
\frac{D}{4}=x^2-1\cdot y & ≧0\\
\Rightarrow \space \color{red}y & \color{red}{≦x^2 \cdots②}
\end{split}
■軸(\(\small t=-x\))が\(\small y\)軸、すなわち\(\small x=0\)の場合
\(\small x=0\)を問題の方程式である\(\small t^2+2xt+y=0\)に代入すると、
\begin{split}
t^2+y=0\\
\Rightarrow \space t^2=-y
\end{split}
上記の2次方程式が\(\small t>0\)で解を持つためには、\(\small \color{red}{y<0\cdots③}\)
条件の不等式を図示する
STEP2の結果を整理すると
\begin{cases}
x>0\mathbf{のとき、}y<0 \cdots①\\
x=0\mathbf{のとき、}y<0 \cdots③\\
x<0\mathbf{のとき、}y≦x^2 \cdots②\\
\end{cases}
図示の結果は順像法と同様のため割愛。
包絡線を利用した解き方
解き方紹介のときにも触れた通り、理屈含めた理解は大学数学の範疇なので、ここでは解き方だけの紹介にとどめておきます。
■包絡線を利用した解法手順
・STEP1:問題の方程式を変数で微分
・STEP2:元の方程式と微分した方程式から変数を消去 →包絡線が求まる
・STEP3:接点の座標を求めることで、包絡線の接線群を図示(\(\small =\)通過領域)
問題の方程式を変数で微分
\(\small t^2+2xt+y=0\cdots①\)を変数\(\small t\)で微分すると、
\begin{split}
2 &t+2x=0\\
\Rightarrow \space t&=-x\cdots②
\end{split}
元の方程式と微分した方程式から変数を消去
②を①に代入して変数\(\small t\)を消去すると
\begin{split}
(-x)^2+2x\cdot(-x)+y&=0\\
\Rightarrow \space x^2-2x^2+y&=0\\
\Rightarrow \space y&=x^2\\
\end{split}
この\(\small y=x^2\)が包絡線になります。
接点の座標を求めることで、包絡線の接線群を図示
包絡線が求まったので、包絡線\(\small y=x^2\)の\(\small x=k\)における接線の方程式を考えます。接点\(\small (k,k^2)\)における接線の方程式から
\begin{split}
y&=2k(x-k)+k^2\\
\Rightarrow \space &y=2kx-k^2\\
\Rightarrow \space &k^2-2kx+y=0\\
\Rightarrow \space &(\color{red}{-k})^2+2x\cdot(\color{red}{-k})+y=0\cdots③\\
\end{split}
③と①を比較すると\(\small k=-t\)であることが分かるので、問題の式は\(\small y=x^2\)の点\(\small (-t,t^2)\)(\(\small t>0\))における接線群であると捉えることができます。
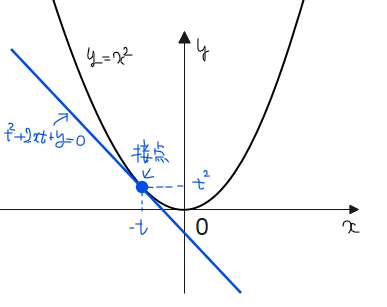
問題の式 \(\small \color{blue}{t^2+2xt+y=0}\)になる。
\(\small t\)の値が変われば接線が変わる(接線群)。
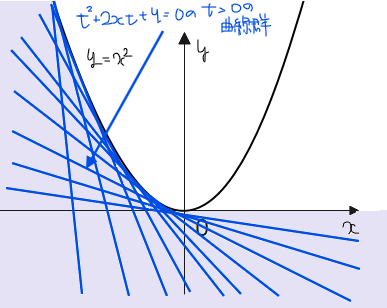
よって、\(\small t>0\)なので、接点\(\small (-t,t^2)\)は\(\small x\)座標が負の領域を動くので、接線群を図示すると以下のようになり、通過領域が求まります。
おすすめな解法は?
ここまで、通過領域を求める3つの解き方を紹介しましたが、「結局どれがおすすめなの?」と思った人も多いと思います。ここでは個人的な独断と偏見でおすすめを紹介します。
結論は、「順像法(ファクシミリ法)」がおすすめです。おすすめする主な理由は以下の2つです。
- 考え方がシンプルで分かりやすい
- 汎用性が高い
1点目は、順像法は通過領域を\(\small x=k\)で切断したときの\(\small y\)の範囲を求めるという方法なので、いわゆる「最大最小値問題」として解くことができます。一方で、逆像法はいわゆる「解の配置問題」といって、方程式の解を指定の範囲に持つ条件を求める問題に置き換えて解くという考え方が若干複雑で混乱します。
2点目の汎用性については、順像法は最大最小値問題になるので、微分することでどんな方程式であっても求めることができます。一方で、逆像法では、解の配置問題として解くことになるので、2次方程式などであればそれほど大変ではないのですが、3次方程式や三角関数など単純ではない方程式については条件の検討がかなり大変です。
包絡線を利用した解法については、変数を消去するのが大変になる可能性があるのと、最終的には図形的な感覚で図示していくことになるので、境界を含む・含まないチェックなど細かい条件が漏れたりするリスクはあるかなと思います。
【問題演習】通過領域の図示
では実践編として入試問題にチャレンジしてみましょう。
正の実数\(\small t\)に対し、座標平面上の2点\(\small \mathrm{P}(0,t)\)と\(\small \displaystyle \mathrm{Q}\left(\frac{1}{t},0\right)\)を考える。\(\small t\)が\(\small 1≦t≦2\)の範囲を動くとき、座標平面内で線分\(\small \mathrm{PQ}\)が通過する部分を図示せよ。 [大阪大]
今回は、順像法による解き方で解説していきます。
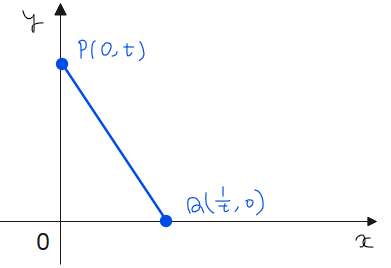
通過領域の断面を考えるために、まずは、線分\(\small \mathrm{PQ}\)を表す方程式を考える。2点を通る直線の方程式より
\begin{split}
y&=\dfrac{0-t}{\dfrac{1}{t}-0}(x-0)+t\\
y&=-t^2x+t\space(1≦t≦2)\cdots①\\
\end{split}
線分\(\small \mathrm{PQ}\)を表す方程式①を\(\small x=k(k≧0)\)で切断したときの\(\small y\)座標は、
\begin{split}
y&=-kt^2+t\space(1≦t≦2)\cdots②\\
\end{split}
なので、この値が変数\(\small t\)によってどの範囲を動くか、つまり最大値、最小値を求めればよい。
(補足)\(\small k\)の範囲について
線分\(\small \mathrm{PQ}\)を\(\small x=k\)で切断することを考えたときに、点\(\small \mathrm{P}\)は必ず\(\small y\)軸上に存在することから、通過領域は\(\small x\)軸の0以上の領域に広がっていることになる点に注意する。
同様に、点\(\small \mathrm{Q}\)は必ず\(\small x\)軸上に存在することから、\(\small y≧0\)であることもわかる。
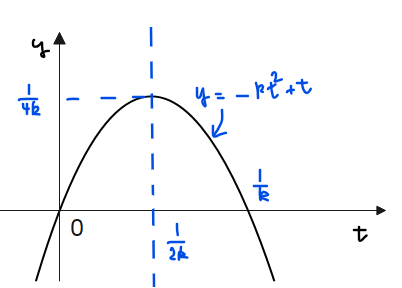
②は\(\small t\)の2次関数とみなすことで、軸が\(\small \displaystyle t=\frac{1}{2k}\)、頂点\(\small \displaystyle \left(\frac{1}{2k},\frac{1}{4k}\right)\)、切片0と分かるので、あとは\(\small 1≦t≦2\)の範囲での最大最小を求めればよい。
[1]軸が\(\small 1≦t≦2\)の範囲外左側の場合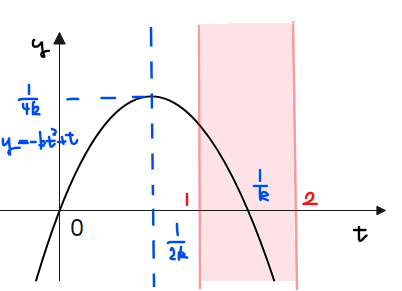
図にすると上記のような場合であり、\(\small \displaystyle \frac{1}{2k}≦1\)が成り立つパターンなので、\(\small \displaystyle \color{red}{\frac{1}{2}≦k\cdots①}\)。このとき、\(\small 1≦t≦2\)の範囲(上図の赤色範囲)での最大最小は明らかに
\begin{cases}
t=1\mathbf{のとき、最大値}-k+1\\
t=2\mathbf{のとき、最小値}-4k+2\\
\end{cases}
なので、不等式で表すならば\(\small \color{red}{-4k+2≦y≦-k+1\cdots①’}\)
[2]軸が\(\small 1≦t≦2\)の範囲内左側の場合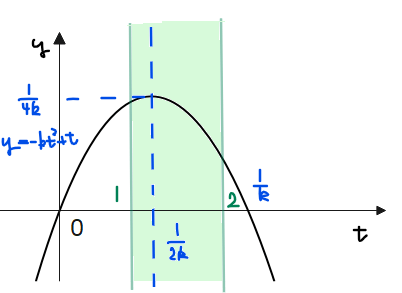
図にすると上記のような場合であり、\(\small \displaystyle 1≦\frac{1}{2k}≦\frac{3}{2}\)が成り立つパターンなので、\(\small \displaystyle \color{red}{\frac{1}{3}≦k≦\frac{1}{2}\cdots②}\)。
このとき、\(\small 1≦t≦2\)の範囲(上図の緑色範囲)での最大最小は
\begin{cases}
t=\frac{1}{2k}\mathbf{のとき、最大値}\frac{1}{4k}\\
t=2\mathbf{のとき、最小値}-4k+2\\
\end{cases}
なので、不等式で表すならば\(\small \color{red}{-4k+2≦y≦\dfrac{1}{4k}\cdots②’}\)
[3]軸\が\(\small 1≦t≦2\)の範囲内右側の場合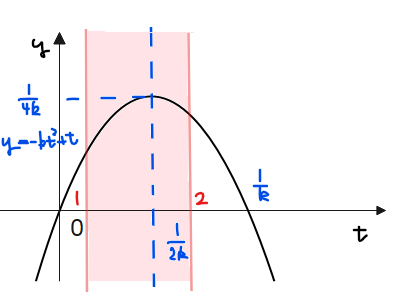
図にすると上記のような場合であり、\(\small \displaystyle \frac{3}{2}≦\frac{1}{2k}≦2\)が成り立つパターンなので、\(\small \displaystyle \color{red}{\frac{1}{4}≦k≦\frac{1}{3}\cdots③}\)。
このとき、\(\small 1≦t≦2\)の範囲(上図の赤色範囲)での最大最小は
\begin{cases}
t=\frac{1}{2k}\mathbf{のとき、最大値}\frac{1}{4k}\\
t=1\mathbf{のとき、最小値}-k+1\\
\end{cases}
なので、不等式で表すならば\(\small \color{red}{-k+1≦y≦\dfrac{1}{4k}\cdots③’}\)
[4]軸が\(\small 1≦t≦2\)の範囲外右側の場合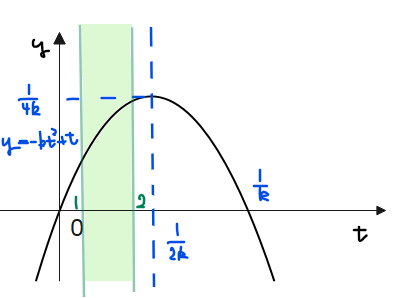
図にすると上記のような場合であり、\(\small \displaystyle 2≦\frac{1}{2k}\)が成り立つパターンなので、\(\small \displaystyle \color{red}{0≦k≦\frac{1}{4}\cdots④}\)。このとき、\(\small 1≦t≦2\)の範囲(上図の緑色範囲)での最大最小は
\begin{cases}
t=2\mathbf{のとき、最大値}-4k+2\\
t=1\mathbf{のとき、最小値}-k+1\\
\end{cases}
なので、不等式で表すならば\(\small \color{red}{-k+1≦y≦-4k+2\cdots④’}\)
以上、①~④および①’~④’の結果と、\(\small \color{red}{x≧0、y≧0}\)(線分\(\small \mathrm{PQ}\)の存在範囲)を加味すると
\begin{split}
&
\begin{cases}
0≦x≦\dfrac{1}{4}\mathbf{のとき、}\color{blue}{-k+1}≦y≦\color{green}{-4k+2}\cdots[4]\\
\dfrac{1}{4}≦x≦\dfrac{1}{3}\mathbf{のとき、}\color{blue}{-k+1}≦y≦\color{red}{\dfrac{1}{4k}}\cdots[3]\\
\dfrac{1}{3}≦x≦\dfrac{1}{2}\mathbf{のとき、}\color{green}{-4k+2}≦y≦\color{red}{\dfrac{1}{4k}}\cdots[2]\\
\dfrac{1}{2}≦x\mathbf{のとき、}\color{green}{-4k+2}≦y≦\color{blue}{-k+1}\cdots[1]\\
\end{cases}\\
&
\begin{cases}
x≧0\\
y≧0\\
\end{cases}
\end{split}
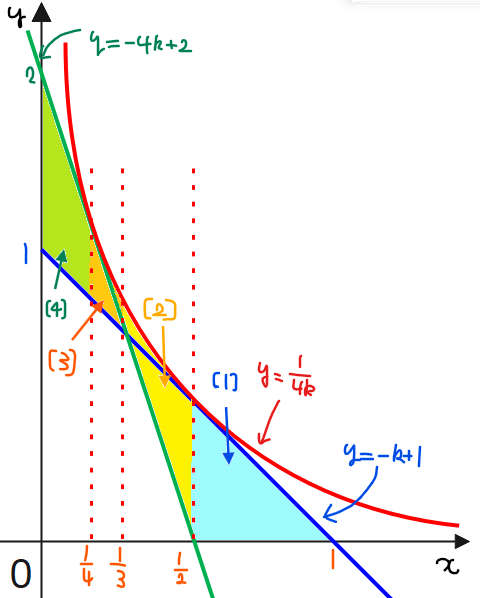
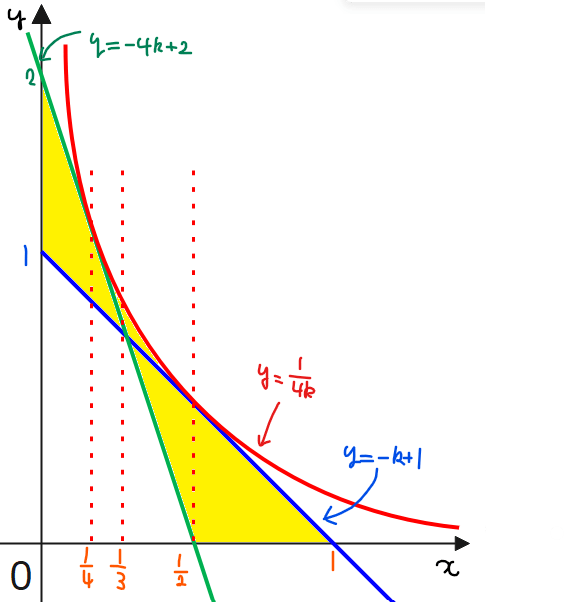
の共通範囲が求める領域となるので、図示すると通過領域は下図の通りとなる(ただし、境界も含む)…(答)。
本記事のまとめ
今回は通過領域の図示の方法について解説していきました。通過領域の図示には「順像法(ファクシミリ法)」、「逆像法」、「包絡線を利用した解法」の主に3種類があり、それぞれの解き方について説明しました。
■順像法の解法手順 ☜ おススメ!!
・STEP1:\(\small x=k\)で切断したときの\(\small y\) 座標の値を求める … \(\small x\)固定
・STEP2:\(\small y\)座標の最大値、最小値を\(\small k\)の式で求める … \(\small y\)の範囲
・STEP3:STEP2の式を\(\small xy\) 平面上に図示する … 範囲の足し合わせ
■逆像法の解法手順
・STEP1:\(\small x、y\)を固定し条件式を変数の方程式に変形
・STEP2:方程式が解を持つための条件を求める
・STEP3:条件の不等式を図示する
■包絡線を利用した解法手順
・STEP1:問題の方程式を変数で微分
・STEP2:元の方程式と微分した方程式から変数を消去 →包絡線が求まる
・STEP3:接点の座標を求めることで、包絡線の接線群を図示(\(\small =\)通過領域)
慣れるまでは問題を繰り返し解き、考え方を掴むことが大事な分野になるので、今回学んだ解き方で他の問題にも挑戦して実力アップをしていきましょう!
では今回はここまでです。お疲れさまでした!







コメント