今回は、重複組み合わせについて解説します。「重複順列と重複組み合わせの違いがわからない…」、「解説を見たら重複組み合わせで解いてるけど、正直なんで重複組み合わせで解けるのかよくわからない…」、「解き方がよくわからない…」など苦手だなと感じている人向けに、根本的な考え方と問題の解き方を分かりやすく解説しているので、ぜひ最後まで読んでみてください!
- 重複順列と重複組み合わせって何が違うの?
- 重複組み合わせってどういうときに使うの?具体的な問題は?
- 重複組み合わせにでてくるHってなに?具体的な計算方法は?
- Hで解いたり、〇と仕切りが出てきたりするけど結局どう解けばいいの?
重複組み合わせの解き方のコツは?
【はじめに】重複組み合わせとは?
重複組み合わせの考え方
重複組み合わせとは何かを説明するときによくあるのが、「異なる\(\small n\)個のものから重複を許して\(\small r\)個を選ぶ組み合わせの総数である」という説明です。
もちろんこの説明自体は正しいです。ですが、個人的にはこの考え方だけだと重複組み合わせの問題を解いていくのは難しいと思っています。なぜならは、重複組み合わせではもう一つの重要な考え方があるからです。
ここでは、まずはじめに重複組み合わせの重要な考え方2つを説明します。
■重複組み合わせの重要な考え方
①異なるものを重複を許して選ぶときの組み合わせの総数
②同じものを自由に分配するときの組み合わせの総数
このことを理解せずに重複組み合わせの問題を解こうとするといろいろと混乱してしまうことになるので、ここでしっかり理解しておきましょう!
考え方①:異なるものを重複を許して選ぶ
1つ目は皆さんもよく知っている通り、ダブりとかを気にせず選んだときの組み合わせです。
たとえば、のどが渇いていて、目の前には「りんごジュース、オレンジジュース、お茶」が入った3種類のペットボトルがたくさん置かれているとします。その中から好きな飲み物を2つ好き勝手に選んでいいよと言われたら皆さんはどんな組み合わせを選びますか?
(りんご、オレンジ)の組み合わせを選ぶ人もいれば(オレンジ、お茶)を選ぶ人もいるでしょう。でもオレンジジュースがすごく好きな人は(オレンジ、オレンジ)と2本とも同じものを選ぶかもしれません。
このように、ダブりも含めた選び方の通り数を求めるのが重複組み合わせです。
考え方②:同じものを自由に分配する
2つ目の考え方は「どういうこと?」と思った人も多いと思います。実はこれが重複組み合わせの2つ目の考え方で、重複組み合わせとしてはあまり意識されていない考え方になります。
この考え方も発想の転換をすると考え方①と同じということが分かるのですが、はじめのうちは別物として考えておいた方が分かりやすいと思います。
この考え方は例えば、お茶のペットボトルが5本余ってしまったので、3人の子どもに分けることにしたとします。分け方は自由で、1人の子どもに5本あげてもいいですし、2本、2本、1本のようにあげてもいいですが、5本はすべて3人の誰かにあげるとします。
このような問題は、1人の人に同じものが重複してわたってもいいという考え方なので重複組み合わせの問題として考えることができます。
具体的な解き方はのちほど解説するので、ここでは「同じもの」を「自由に分配」するときも重複組み合わせが使えるんだなと覚えておきましょう。
重複組み合わせの具体的な計算方法
重複組み合わせには2つの考え方があること解説しました。考え方ごとに解き方も違うので、ここではそれぞれの具体的な計算方法を説明します。
異なるものを重複を許して選ぶ組み合わせ(考え方①)の計算法
さっきの例で考えていきます。
りんごジュース、オレンジジュース、お茶が入った3種類の飲み物がたくさんあり、好きな2本を選んでよいとき、選び方は何通りあるか?
基本的な考え方と計算法
■異なるものを重複して選ぶ組み合わせの計算法
「〇(白丸)」と「|(仕切り)」を一列に並べて計算
この問題は、異なる3種類の飲み物から重複を許して2本を選ぶ組み合わせを求める問題になります。選んだ飲み物が「りんごジュース、お茶」でも「お茶、りんごジュース」でも選び方は同じになるので、順序を気にしないことから組み合わせだと判断します。
まずは基本的な考え方から説明します。いきなりですが、飲み物の個数を白丸(〇)で表し、2本の仕切り(|)を用意して、「〇」×2個と「|」×2本を1列に並べることを考えます。

たとえば上図のようになった場合は、仕切りの一番左側にある白丸の個数を選んだりんごジュースの本数、仕切りの真ん中にある白丸の個数を選んだオレンジジュースの本数、仕切りの一番右側にある白丸の個数を選んだお茶の本数と考えます。
このルールに従って白丸2個と仕切り2本を一列に並べる方法は\(\small \displaystyle \frac{4!}{2!2!}=6\)通りと求めることができます。
(補足)区別できないものを一列に並べる通り数
\(\small n\)個の同じものと\(\small m\)個の同じものを一列に並べる総数は
$$\color{red}{\frac{(n+m)!}{n! \cdot m!}\space \textrm{通り}}$$
(解答)
6通り
今回のように異なるものを重複を許して選ぶ組み合わせの問題では、白丸(〇)と仕切り(|)を使う計算法は結構テクニックが必要で大変なので、次に説明する記号Hを使った計算方法が便利です。
【超簡単】「H」を使った計算法
考え方の基本は先程解説した通りですが、ここでは「異なるものを重複を許して選ぶ組み合わせ」のとても簡単な計算方法について解説します。それが、記号Hを使った計算方法です。
■記号Hを使った重複組み合わせの計算方法 ※おすすめ!
異なる\(\small n\)個から重複を許して\(\small r\)個選ぶ組み合わせの総数は
$$\color{red}{{}_{n}\mathrm{H}_{r}={}_{n+r-1}\mathrm{C}_{r}}$$
Hを使って今回の問題を解いてみましょう。
異なる3種類の飲み物から重複を許して2個選ぶ重複組み合わせなので、
\begin{equation}
\begin{split}
\color{red}{{}_{3}\mathrm{H}_{2}}&\color{red}{={}_{3+2-1}\mathrm{C}_{2}}\\
&={}_{4}\mathrm{C}_{2}=\color{red}{6}\\
\end{split}
\end{equation}
よって、6通り…(答)。
同じものを自由に分配する組み合わせ(考え方②)の計算法
同質なお茶のペットボトル5本を3人の子どもに配るとき、配り方は何通りか?
白丸と仕切りで計算せよ
■同じものを自由に分配する組み合わせの計算法 ※おすすめ!
「〇(白丸)」を「|(仕切り)」で分割せよ!
5本のお茶を3人で分割すると考えます。
お茶を白丸(〇)、仕切り(|)を2本(2本で仕切れば3分割できる)用意することで、「〇」×5個と「|」×2本を一列に並べる通り数を考えればよいので
$$\frac{(5+2)!}{5! \cdot 2!}=\frac{7\cdot 6}{2}=21$$
よって、21通りと求めることができます。
(解答)
21通り
【重複組み合わせの計算方法】考え方ごとのおすすめは?
例題を例に考え方①と考え方②ごとに計算方法を紹介してきました。
いろいろな解き方、計算方法が出てきて混乱したかもしれないので、ここで「結局どうやって解くのがいいの?」という疑問に対して個人的なおすすめをまとめます。
■異なるものを重複を許して選ぶ組み合わせ
\(\small \color{red}{{}_{n}\mathrm{H}_{r}}\)を活用せよ!
■同じものを自由に分配する組み合わせ
「〇」を「|」(仕切り)で分割せよ!
このように、記号Hを使うときと白丸(〇)と仕切り(|)を使うときを分けて考えるのがおすすめです。
記号Hはいわゆる重複組み合わせでよく出てくるダブりokで選ぶ組み合わせを考えるときに非常に便利です。新しい公式が出てきてはじめは大変ですが、すぐに計算自体は慣れると思います。逆にこの問題を白丸(〇)と仕切り(|)で解くのは例題でも解説しましたが結構大変ですよね…。
一方で、同じものを自由に分配する組み合わせの総数は、重複順列の基本的な考え方である白丸(〇)と仕切り(|)を使った考え方の方が分かりやすいと思います。逆に記号Hを使って計算することも可能ですが感覚的にわかりずらいので個人的にはおすすめしません。
重複順列と重複組み合わせの違い
重複順列と重複組み合わせの違いは、一般に順番を気にするか気にしないかだと考えられています。順番を気にする場合は重複順列、順番を気にしない場合は重複組み合わせという見分け方です。
では以下の問題がそれぞれどちらの考え方で解けるか考えてみましょう。
【例題で確認】重複順列と重複組み合わせの見分け方
(1) 3人の人を部屋Aと部屋Bに入れる分け方は何通りあるか?ただし、一人も入らない部屋があってもよいものとする。
(2) 3つの同質なボールを2人に配る方法は何通りあるか?ただし、ボールをもらえない人がいてもよいものとする。
どうでしょうか?「え、やっぱりよくわからない…」と思った人も大丈夫です。問題のどこを見て判断すればいのか、このあとの解説で一緒に確認していきましょう!
問題1:異なるものを自由に分配する通り数
3人の人を部屋Aと部屋Bに入れる分け方は何通りあるか?ただし、一人も入らない部屋があってもよいものとする。
まずは問題文最後の「ただし、一人も入らない部屋があってもよいものとする。」という部分に注目します。仮に3人の人がXさん、Yさん、Zさんだとすると、Xさんが部屋Aで、Yさんも部屋A、Zさんも部屋AでもOKということです。同じ部屋を選んでよいということから「重複」の問題だということが分かります。
重複の問題だと分かったらあとは、順列なのか組み合わせなのかを見分けていきます。が、この問題を読んでもわかる通り順番を付けたり、並べたりはしていません。
実はこの問題は重複順列で解けるのですが、重複順列と重複組み合わせの見分ける基準が、重複okで順番を気にする場合(つまり並べる必要がある)は「重複順列」、順番を気にしない(つまり組み合わせのみ)場合は「重複組み合わせ」という考え方では見分けることができません。
見分けるためには重複順列を以下のように捉えることが重要になります。
■重複順列の重要な考え方
①異なるものを重複を許して選び並べる
②異なるものを自由に分配する
重複順列にも重複組み合わせと同じように②の考え方があることを覚えておきましょう。
今回は、「3人」という「異なるもの」を部屋A、Bに「自由に分配」(=自由に分ける)するパターンなので重複順列の考え方②が使えます。
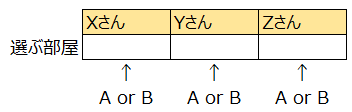
よって、3人がそれぞれ部屋A、部屋Bのどちらの部屋に行くかの2通りが考えられるので、\(\small \color{red}{2^3}= 2 \times 2 \times 2 = \color{red}8\)通りが求める場合の数になります。
(解答)
8通り
問題2:同じものを自由に分配する通り数
3つの同質なボールを2人に配る方法は何通りあるか?ただし、ボールをもらえない人がいてもよいものとする。
こちらもまずは問題文の最後に「ボールをもらえない人がいてもよい」とあるので、ボールが同じ人に複数わたる可能性があることから重複の問題だということが分かります。
では重複順列と重複組み合わせのどちらなのかということですが、「3つのボールのそれぞれが、Xさん、Yさんのどちらに行くかの2通りがあると考えると、重複順列で\(\small 2^3=8\)通り!」と思った人は要注意です。この考え方は間違いです。なぜかというと、上記の考え方では、以下のように同じ配り方になるパターンが含まれてしまうからです。

ポイントは、「同質なボール」が3つなので、上記のようにボール自体を区別してしまうとダメなわけです。上図①のパターンだとXさんはボール1と2、Yさんはボール3を持っていて、②のパターンだとXさんはボール1と3、Yさんはボール2を持っていますが、ボール自体は見分けがつかないのでどちらもXさんがボール2個、Yさんがボール1個という配り方になり、同じ1通りというわけです。
このような場合は、重複組み合わせの考え方②「同じものを自由に分配するときの組み合わせの総数」を利用します。
下図のように「3つのボールを2分割」=「3つの白丸(〇)を1つの仕切り(|)で2分割」と考えて、仕切り棒より左側の〇の個数をXさんに配る個数、右側の〇の個数をYさんに配る個数と考える、これが「同じものを自由に分配する組み合わせの計算方法」でした。

上図のように、3つの白丸(〇)と仕切り(|)が上図のように「〇|〇〇」と並んだ場合は、Xさんにボールが1個、Yさんにボールが2個配られる場合と考えるわけです。「|〇〇〇」という並びであれば、Yさんにボールが3個配られる(Xさんはボール0個)場合になります。
3つの白丸(〇)と仕切り(|)を1列に並べる計算自体は、同じものを含む順列計算なので、\(\small \displaystyle \color{red}{\frac{4!}{3! 1!}=4}\)通りと求めることができます。
【まとめ】重複順列と重複組み合わせの見分け方
それぞれの違いを整理すると以下の通りです。特に②の分配の考え方を見分けるのが苦手な人が多いので分配されるものが「同じもの」なのか「異なるもの」なのかに注意して判断するようにしましょう。
■重複順列と重複組み合わせの見分け方
①-1:異なるものを重複を許して選ぶ→重複組み合わせ
①-2:異なるものを重複を許して選び並べる→重複順列
②-1:同じものを自由に分配する→重複組み合わせ
②-2:異なるものを自由に分配する→重複順列
【問題演習】重複組み合わせの基本問題7選
ここからは重複組み合わせでよくでてくる基本問題を解説していきます。考え方ごとの「重複組み合わせの計算法」を意識して解けるか確認してみましょう。
選ぶ・分けるの基本問題
(1) \(\small a, b, c, d\)の4つの文字から重複を許して3つ選ぶ場合、選び方は何通りあるか。
(2) 6つのお菓子を\(\small A, B, C, D\)の4つの袋に分ける方法は何通りあるか。ただし、一つも入れない袋があってもよいものとする。
(3) \(\small (x+y+z)^5\)の展開式の異なる項の数を求めよ。
問題1:選ぶ問題
\(\small a, b, c, d\)の4つの文字から重複を許して3つ選ぶ場合、選び方は何通りあるか。
異なるものから重複を許して選ぶ問題(並べない)なので「見分け方:①-1」より重複組み合わせが使えるので、\(\small {}_{4}\mathrm{H}_{3}={}_{6}\mathrm{C}_{3}=20\)通り…(答).

上図のように「〇」×3個と\(\small a, b, c, d\)を区分けするための仕切り(|)×3本を一列に並べる計算から
\begin{equation}
\begin{split}
\frac{(3+3)!}{3!\cdot 3!}&=\frac{6\cdot 5\cdot 4}{3\cdot 2}\\
&\color{red}{=20通り\cdots(答)}
\end{split}
\end{equation}
問題2:分ける問題
6つのお菓子を\(\small A, B, C, D\)の4つの袋に分ける方法は何通りあるか。ただし、一つも入れない袋があってもよいものとする。
見分けがつかない同じもの(=お菓子)を4つの袋に自由に分ける問題なので「見分け方:②-1」より重複組み合わせが使えると判断できます。
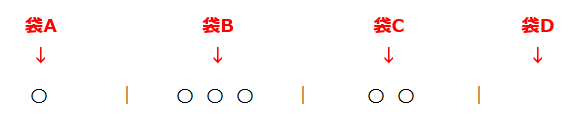
分ける問題は「〇」と「|」で分割すればよいので、今回であれば、6つのお菓子を6つの「〇」として、仕切り3つで4分割すればよいので、
\begin{equation}
\begin{split}
\frac{(6+3)!}{6!\cdot 3!}&=\frac{9\cdot 8\cdot 7}{3\cdot 2}\\
&\color{red}{=84通り\cdots(答)}
\end{split}
\end{equation}
問題3:展開式の項の種類
\(\small (x+y+z)^5\)の展開式の異なる項の数を求めよ。
問題で聞かれていることが若干難しいのまずはそこを補足します。
\(\small (x+y+z)^5\)を展開したあとに出てくる項には、\(\small x^5\)や\(\small x^3yz\)、\(\small xy^2z^2\)など他にもたくさんの種類があり、全部で何種類あるか?というのがこの問題で聞かれていることになります。
では項の種類はどう決まるのでしょうか?5乗だと大きいので仮に\(\small (x+y)^3\)で考えてみます。これは展開すると
$$(x+y)^3=x^3+3x^2y+3xy^2+y^3$$
となり、4種類の項が出てきます。ここで、たとえば\(\small x^2y\)の項はどのようにしてできた項かを考えてみます。そもそも展開とは、それぞれの括弧から\(\small x\)や\(\small y\)を選んできてかけ算するものでした。
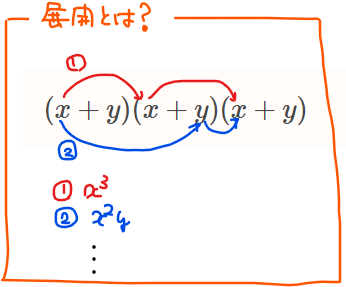
上図①のように、3つの括弧すべてから\(\small x\)を選べば\(\small x^3\)の項になりますし、②のように選べば\(\small x^2y\)になります。この考え方を用いると、\(\small x^2y\)の項は下図のように\(\small (x+y)\)の3つのかけ算の項のうち、\(\small x\)を2個、\(\small y\)を1個選んで展開してたものが\(\small x^2y\)の項になることが分かります。
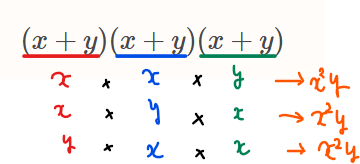
この考え方は他の種類の項についても同じことがいえるので、展開後の項の種類が知りたければ、\(\small x, y\)の2種類の文字から重複を許して3個(3乗なので)を選ぶ通り数を求めればよいことになるわけです。実際に計算すると、\(\small {}_{2} \mathrm{H}_3={}_{4} \mathrm{C}_3=4\)通りとなり、さっき展開した種類の数と一致することが分かります。
長くなりましたが、本題に戻って、今の考え方を用いると、\(\small (x+y+z)^5\)の場合は、\(\small x, y, z\)の3種類の文字から重複を許して5個を選ぶ通り数なので、、\(\small {}_{3} \mathrm{H}_5={}_{7} \mathrm{C}_5={}_{7} \mathrm{C}_2=\color{red}{21}\)通り…(答)となります。
整数解の個数
(1) \(\small x, y, z\)を非負の整数とするとき、\(\small x+y+z=5\)を満たす整数解の組\(\small (x,y,z)\)の個数はいくつか。
(2) \(\small x, y, z\)を\(\small x≧1, y≧0, z≧2\)を満たす整数とするとき、\(\small x+y+z=5\)を満たす整数解の組\(\small (x,y,z)\)の個数はいくつか。
(3) \(\small x, y, z, w\)を正の整数とするとき、\(\small x+y+z+w≦6\)を満たす整数解の組\(\small (x,y,z,w)\)の個数はいくつか。
(4) \(\small x, y, z\)を非負の整数とするとき、\(\small 2≦x+y+z≦4\)を満たす整数解の組\(\small (x,y,z)\)の個数はいくつか。
問題1:\(\small x,y,z\)が非負の整数解の個数
\(\small x, y, z\)を非負の整数とするとき、\(\small x+y+z=5\)を満たす整数解の組\(\small (x,y,z)\)の個数はいくつか。
「非負の整数」とは「マイナスにならない整数」というのとなので、\(\small x≧0,y≧0,z≧0\)ということ。\(\small x,y,z\)を足して5になるということは見方を変えれば、5個のものを\(\small x\)さん、\(\small y\)さん、\(\small z\)さんの3人に自由に分ける(もらえない人がいてもよい)ことと同じです。
どういうことかというと、たとえば、\(\small (x,y,z)=(2,0,3)\)という整数解は、5個のものを\(\small x\)さんに2個、\(\small y\)さんには0個、\(\small z\)さんに3個分けるという状況とみなすことができます。
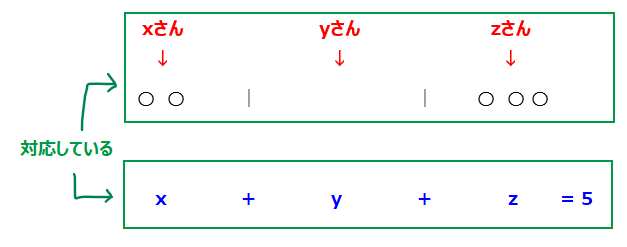
よって、「5個のものを3人に自由に分ける」と考えると、「〇」×5個、「|」×2本を1列に並べる通り数を求めればよいので
$$\frac{(5+2)!}{5!\cdot2!}=\frac{7\cdot6}{2}=\color{red}{21通り\cdots(答)}$$
問題2:\(\small x,y,z\)に条件が付く整数解の個数
\(\small x, y, z\)を\(\small x≧1, y≧0, z≧2\)を満たす整数とするとき、\(\small x+y+z=5\)を満たす整数解の組\(\small (x,y,z)\)の個数はいくつか。
■条件付きの整数解の個数
\(\small x≧n\)のような条件がある場合は、\(\small \color{red}{X=x-n}\)とおいて\(\small X≧0\)の形を作り出せ!
さっきの問題と違うのは、\(\small x \color{red}{≧1}, y≧0, z\color{red}{≧2}\)の部分です。なので、\(\small \color{red}{x-1≧0}, y≧0, \color{red}{z-2≧0}\)として、\(\small x-1=X, z-2=Z\)とおけば、\(\small \color{red}{X≧0, y≧0, Z≧0}\)となり問題1の条件と同じ状態にすることができます。
\(\small x+y+z=5\)の式も
\begin{equation}
\begin{split}
(x\color{red}{-1})\color{red}{+1}+y+(z\color{red}{-2})\color{red}{+2}&=5\\
X+y+Z+3&=5\\
X+y+Z&=2\\
\end{split}
\end{equation}
と変形することで、もともとの問題は「\(\small \color{red}X≧0, y≧0, \color{red}Z≧0\)を満たす整数\(\small X,y,Z\)に対して、\(\small \color{red}X+y+\color{red}Z=2\)を満たす整数解の組\(\small (X,y,Z)\)の個数を求めよ」という問題に置き換えることができます。
よって、解き方自体は問題1と同様で、「〇」×2を2本の仕切り(|)で分割する通り数を求めればよいので
$$\frac{(2+2)!}{2!\cdot2!}=\frac{4\cdot3}{2}=\color{red}{6通り\cdots(答)}$$
問題3:不等式の整数解の個数
\(\small x, y, z, w\)を正の整数とするとき、\(\small x+y+z+w≦6\)を満たす整数解の組\(\small (x,y,z,w)\)の個数はいくつか。
■不等式の整数解の個数
補充役を用意して等式に持ち込め!
今度は考える式が不等式になっているのが大きな違いです。もちろん、\(\small x+y+z+w=1\)の場合、\(\small x+y+z+w=2\)の場合、…、\(\small x+y+z+w=6\)の場合と6個分をそれぞれ計算して合算しても求めることができますが大変です。
このような問題では、0以上の整数\(\small r\)を導入して、\(\small x+y+z+w\color{red}{+r}=6\)という等式に無理やり置き換えると簡単になります。どういうことかというと、\(\small x+y+z+w≦6\)ということは、\(\small x+y+z+w\)だけだと3や4のように6に足りていない部分が出てしまうので、足りない分の「補充役」として整数\(\small r\)を導入することで、たとえば\(\small x+y+z+w=4\)であれば\(\small r=2\)を補充することで、\(\small x+y+z+w+r=6\)の等式の問題として考えることができるようになります。
この考え方を使って今回の問題を解いていきます。まずは、\(\small x, y, z, w\)は正の整数という条件があるので、\(\small x≧1、y≧1、z≧1、w≧1\)となります。
(補足)ややこしい条件の言い回しを覚えよう
・正の整数 …1以上の整数(0は正でも負でもない数)
・非負の整数…マイナスではない整数ということなので、0以上の整数
\(\small r\)を\(\small r≧0\)を満たす整数とすると、問題の不等式を満たす整数解の個数を求めるということは、\(\small x+y+z+w+r=6\)を満たす整数解の個数を求めることと同義です。
\(\small X=x-1、Y=y-1、Z=z-1、W=w-1\)とおくと、\(\small x≧1、y≧1、z≧1、w≧1\)は\(\small X≧0、Y≧0、Z≧0、W≧0\)となり、
\begin{equation}
\begin{split}
&x+y+z+w+r=6\\
&(x\color{red}{-1})\color{red}{+1}+(y\color{red}{-1})\color{red}{+1}+(z\color{red}{-1})\color{red}{+1}+(w\color{red}{-1})\color{red}{+1}+r=6\\
&X+Y+Z+W+r=2\\
\end{split}
\end{equation}
となるので、「〇」×2個を仕切り4本で5分割する通り数なので
$$\frac{(2+4)!}{2!\cdot4!}=\frac{6\cdot 5}{2}=\color{red}{15通り\cdots(答)}$$
問題4:不等式の整数解の個数(2)
\(\small x, y, z\)を非負の整数とするとき、\(\small 2≦x+y+z≦4\)を満たす整数解の組\(\small (x,y,z)\)の個数はいくつか。
\(\small x, y, z\)は非負の整数なので、\(\small x≧0、y≧0、z≧0\)。
解き方の方針としては、\(\small x+y+z≦4\)を満たす整数解の個数から、\(\small x+y+z≦1\)を満たす整数解の個数を引き算したものが今回求める範囲の個数になることを利用します。
[1]\(\small x+y+z≦4\)を満たす整数解の個数
\(\small r\)を\(\small r≧0\)を満たす整数とすると\(\small x+y+z+r=4\)を考えればよいので、「〇」×4個を仕切り3つで4分割する通り数は、\(\small \displaystyle \frac{(4+3)!}{4!\cdot 3!}=\frac{7\cdot6\cdot5}{3\cdot 2}=35\)通り…①.
[2]\(\small x+y+z≦1\)を満たす整数解の個数
\(\small w\)を\(\small w≧0\)を満たす整数とすると\(\small x+y+z+w=1\)を考えればよいので、「〇」×1個を仕切り3つで4分割する通り数は、\(\small \displaystyle \frac{(1+3)!}{3!\cdot 1!}=4\)通り…②.
①-②より、31通り…(答).
【ここで差がつく】重複組み合わせの応用問題2選
問題1:大小関係に関する重複組み合わせ
さいころを4回投げて\(\small k\)回目に出た目を\(\small a_k \space (k=1,2,3,4)\)とする。
(1) \(\small a_1 < a_2 < a_3 < a_4\)となる目の出かたは何通りか。
(2) \(\small a_1≦a_2≦a_3≦a_4\)となる目の出かたは何通りか。
[福岡大改題]
大小関係を意識して、\(\small (1,2,3,4)\)、\(\small (1,3,4,5)\)、\(\small (1,4,5,6)\)、…と洗い出していくのは大変ですが、少し発想を転換すると簡単に求めることができます。
さいころの6つの目の中から4つを選んでから、小さい順に並べるという発想です。たとえば、\(\small (1,5,3,2)\)を選んだとします。そして出た目を小さい順に並べ替えると\(\small (1,2,3,5)\)のように問題の条件を満たす組み合わせになります。
このように4つの目を選び小さい順に並べ替えることで\(\small a_1 < a_2 < a_3 < a_4\)を満たす組を作ることができるので、6つの目から4つを選ぶ組み合わせの総数を計算すればよいことになります。よって、求める通り数は\(\small {}_{6}\mathrm{C}_4=\color{red}{15}\)通り…(答).
ちなみに、この問題自体は重複組み合わせではなく普通の組み合わせの問題です。
問題(1)との違いは、不等号にイコールが入っている点で、たとえば、先程と違って\(\small (1,\color{red}{2,2},4)\)といったパターンもokになります。これによって、先程は6つの目から4つを選ぶ通り数を考えればよかったのですが、今回は選ぶ目が\(\small (1,\color{red}{2,2},4)\)のように重複してもokなので、重複組み合わせで考える必要があります。
よって、考えるべきは6つのサイコロの目から重複を許して4つの目を選ぶ組み合わせ数なので、\(\small \displaystyle {}_{6}\mathrm{H}_4={}_{9}\mathrm{C}_4=\frac{9 \times 8 \times 7 \times 6}{4 \times3 \times 2}=\color{red}{126}\)通り…(答).
問題2:さいころの応用問題
サイコロを\(\small n\)個同時に投げるとき、出た目の数の和が\(\small n+3\)になる確率を求めよ。 [京都大]
文字が多くて分かりにくいですが、冷静に考えると\(\small n\)個のサイコロを投げたときの和は、どんなに小さくても\(\small n\)になります(すべてのサイコロの目が1だった場合が最も小さい)。
今回は\(\small n\)個のさいころを投げたときの和が\(\small n+3\)ということは、\(\small n\)個のサイコロのうち何個かが1より大きくて「+3」を稼いだことになります。
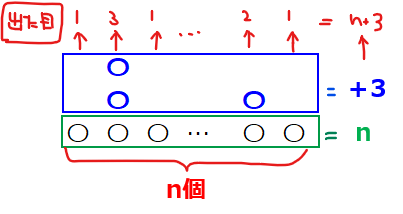
1例として上図であれば、どのサイコロも必ず1以上の目は出るのは確定していて(緑枠部分)、左から2つ目のサイコロは3が出たので1よりも「+2」(青丸が2つ)、右から2つ目のサイコロは2が出たので1よりも「+1」(青丸1つ)で、全体の目の和が \(\small \color{green}n\color{blue}{+3}\)になるわけです。
つまり、今回の問題は、\(\small n\)個のサイコロに3つの青丸を自由に振り分ける組み合わせの総数と考えることができます(もっと言うと\(\small n\)人の人に3つのボールを自由に分ける問題と同じ)。
よって、3つの「〇」を\(\small n-1\)個の仕切りで分割すればよいので
$$\frac{(3+(n-1))!}{(n-1)!\cdot 3!}=\frac{(n+2)(n+1)n}{3!}=\color{red}{\frac{n(n+1)(n+2)}{6}\cdots(答)}$$
まとめ
今回は重複組み合わせの考え方と実際の問題の解き方について解説しました。
今回のポイントを整理すると大きく以下の3つになります。
■重複組み合わせの重要な考え方
①異なるものを重複を許して選ぶときの組み合わせの総数
②同じものを自由に分配するときの組み合わせの総数
■考え方ごとの計算方法
★考え方①:異なるものを重複を許して選ぶ組み合わせ
\(\small \color{red}{{}_{n}\mathrm{H}_{r}}\)を活用せよ!
★考え方②:同じものを自由に分配する組み合わせ
「〇」を「|」(仕切り)で分割せよ!
■重複順列と重複組み合わせの見分け方
①-1:異なるものを重複を許して選ぶ→重複組み合わせ
①-2:異なるものを重複を許して選び並べる→重複順列
②-1:同じものを自由に分配する→重複組み合わせ
②-2:異なるものを自由に分配する→重複順列
今回取り上げた問題は重複組み合わせの中でも頻出な問題ばかりなので、それぞれの解き方が理解できるようになるまで繰り返し演習して解き方をマスターしてみてください。
それでは今回はここまでです。お疲れさまでした!





コメント