【数学徹底解説】積の法則、和の法則の使い分け（場合の数、確率）

今日は確率の場合の数を求めるときに頻出の積の法則と和の法則の使い分けを説明します。

広告

広告

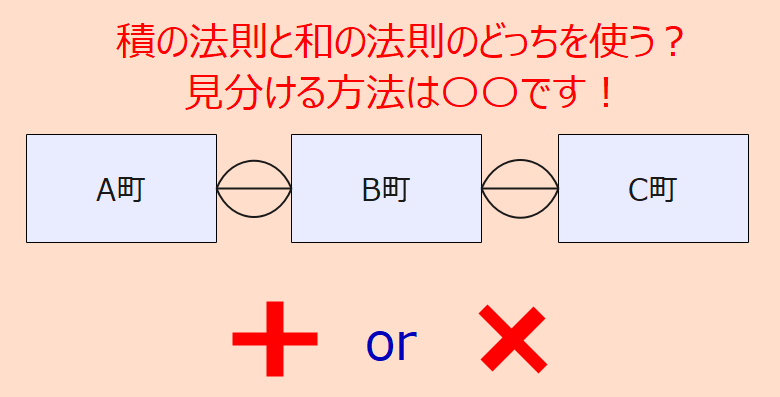
積の法則と和の法則の使い分け

積の法則と和の法則のどちらを使うかの判断ポイントをまとめました。

和の法則を使った問題(1)

例題を通して、使い分けを説明していきます。

ちょっと待ってください。どちらも使っていないと思いましたか？実は、今回は和の法則を使っています。
きっと答えにたどり着くまでに以下のように考えたはず。

このように、当たり前にそれぞれの場合を足し合わせしていたと思います。この足し合わせの作業を、数学では「和の法則」と 呼んでるだけなんです。この例では、サイコロの目が3の倍数になるのは3か6の目が出た場合で、1回サイコロを振ったときに、3か6のどちらか一方だけの目が出ますよね（3も6も両方でてしまうことはない）。

これが、和の法則を使うときのポイントである片一方だけ起こる場合があるということです。

和の法則を使った問題(2)

積の法則を使った問題

例題3

下図のように、A町からB町を経由してC町まで行く場合、そのルートは何通りか。

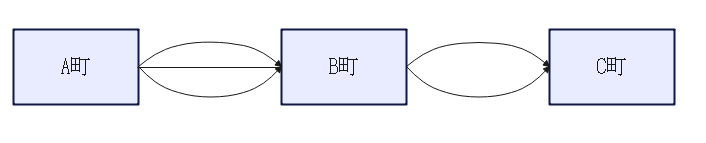
解答

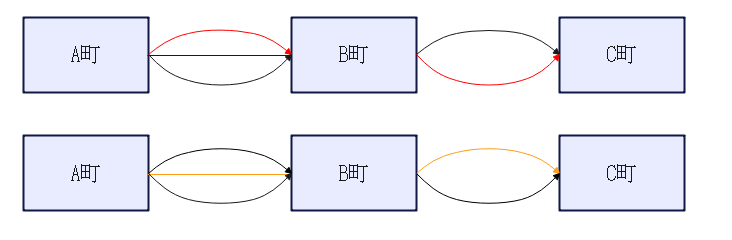
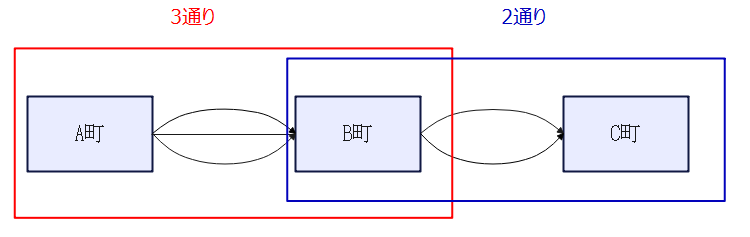
A町からB町までのルートは3通り、B町から、C町までのルートは2通りです。では、今回は、積、和の法則どちらを使えばよいのでしょうか。例えば、下図のように、赤色の道で行くこともあれば、オレンジ色の道で行くこともあります。ただ、いずれの場合も、A町からB町、B町からC町の両方を通ります。A町からB町だけのルートやB町からC町までのルートだけでは、A町からC町まではたどり着けません。

このような場合、2つのルートは必ずどちらも通る（片一方だけ起こることはない）ので、積の法則を使います。

よって、答えは、3 × 2 = 6通りです。

積の法則/和の法則を用いた実践問題

最後にまとめの1問で終わりにしましょう。