【格子点の個数】平面座標上の格子点を求める基礎的アプローチと入試問題の典型パターンの攻略法

今回は、数列の難関分野の一つである格子点の個数に関する問題について解説していきます。

シグマの諸公式（数列の和）を学習するといきなり出てくるのが格子点の個数を求める問題です。解き方に関する解説はあまり学校では教えられることがなく、問題集を解くときにはじめて出てきて苦戦する人も多いと思います…。

そこで本記事では、平面座標上の格子点を求める問題を解く上で最低限知っておくべき基礎的な考え方やシグマ計算のコツについてわかりやすく解説していきます。また、基本問題から入試問題まで難易度別に問題パターンとその攻略法も徹底解説していきますので、ぜひ最後まで確認してみてください！

　本記事はこんな人におすすめ

格子点の個数の求め方を知りたい人
シグマを使った計算方法のコツを知りたい人
格子点の問題の典型パターンを知りたい人
場合分けや対称性の利用など典型問題への攻略法を知りたい人

　本記事のレベル

重要度

低

余力あれば

普通

必須

高
難易度

易しい

易

やや易

やや難

難

難しい
暗記/理解

暗記重視

暗記

半々

理解

理解重視

【徹底解説】格子点の問題の基礎知識
【問題＆解説】格子点に関する問題
本記事のまとめ

【徹底解説】格子点の問題の基礎知識

【講義1】格子点とは？

そもそもですが、格子点って何か説明できますか？少しでも怪しいなと思った人はここで意味を復習しておきましょう。

Point：格子点とは

$\small x$座標、$\small y$座標がともに整数である点のことを格子点と呼ぶ。

具体的にいえば、点$\small (1,2)$や点$\small (-2,0)$、点$\small (3,-1)$などは格子点ですが、点$\small \displaystyle \left( \frac{3}{2},1\right)$や点$\small (-3, \sqrt{2})$などは座標に分数や無理数といった整数ではない数が含まれるので格子点ではないということです。

座標平面上に点を打ったときに格子模様に見えることから格子点という名前が付けられています（そのままですが…）。

【講義2】格子点の個数の求め方（例題）

格子点に関する問題の9割は個数を求める問題といっても過言ではありません。格子点の個数計算自体は大変ですが、求め方の手順は意外とシンプルでたったの2ステップしかありません。

Point：領域内の格子点の個数の求め方

・STEP1：直線$\small x=k$（または$\small y=k$）上の格子点の個数を求める
・STEP2：$\small k$の範囲で総和$\small \left(\sum \right)$を計算する

それぞれのステップの内容については、実際に例題を通して解説していきます。

例題:対称性のある領域内の格子点

$\small y≧0,x+y≦3,-x+y≦3$を満たす領域内にある格子点の個数を求めよ。

本問は、問題自体は簡単ですが入試レベルの応用問題を解く際に重要となる「場合分け」や「図形の性質を利用した数え上げ」などの考え方が詰まっているので例題として取り上げました。

そのため、この問題に正解できるかどうかではなく、この問題をどう解いたか？が非常に重要です。例題を通して考え方のエッセンスを理解するようにしてください。

　解説

まずは不等式で表された領域を図示しておきます。

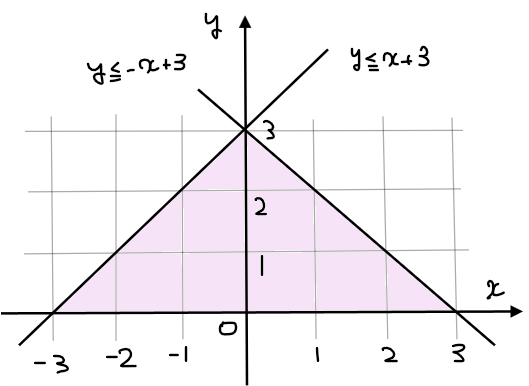
紫部分が今回の不等式で表された領域です。このくらいの個数であれば1つずつ数え上げることもできますが、入試レベルの問題を解くときに必要となる考え方の基礎を理解する意味でも、【講義2】格子点の個数の求め方の手順に沿って解けるようにしておきましょう。

STEP

直線$\small x=k$上の格子点の個数を求める

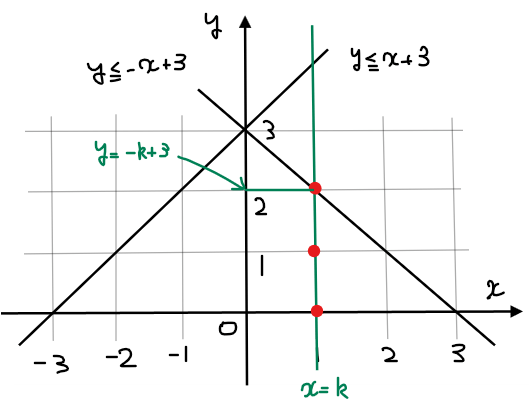
求める領域を直線$\small x=k$（ただし$\small k=-3,-2,-1,0,1,2,3$）で切断したときに線上にある格子点の個数をカウントしていきます（ちなみに、$\small 4≦k$や$\small k≦-4$以下は求める領域外なので無視してOK）。

たとえば、$\small k=1$の場合（直線$\small x=1$）であれば、上図のように$\small x=1$上にある格子点は$\small (1,0),(1,1),(1,2)$の3つです。これは図を見て数え上げる求め方ですが、もう少し深堀してこの「3つ」という数字を数式計算で求められないかを考えてみましょう。

直線$\small x=1$上にある格子点は、一番下にあるのが$\small x$軸上にある$\small y$座標が0の格子点、一番上にあるのが直線$\small y=-x+3$上にある$\small y$座標が2の格子点です。ここで格子点は座標の値が整数である点だったので、直線$\small x=1$上にある格子点の個数が知りたければ、$\small y$座標の範囲である$\small 0≦y≦2$の範囲に、整数となる$\small y$の値がいくつあるのかを計算すればよいわけです。

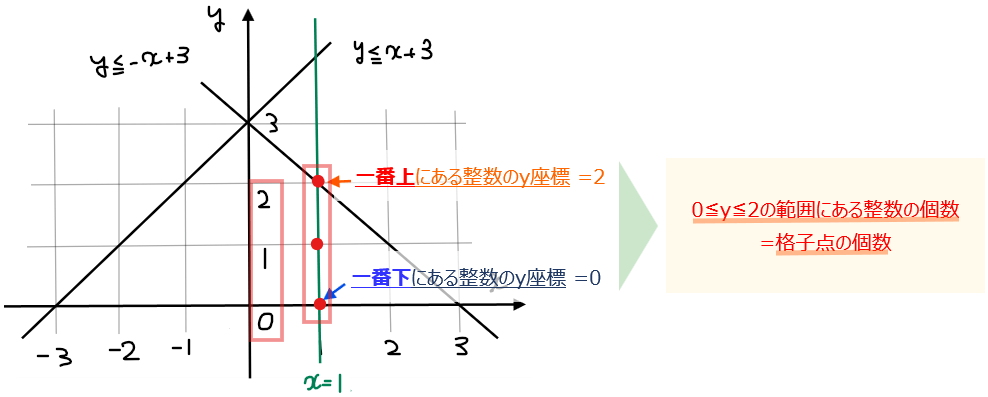
よって、（格子点の個数）$\small =2-0+1=3$と求まります（詳細は、【講義3】格子点の個数の求め方を参照）。0と2の差ではなく個数なので、最後に『＋1』するのを忘れないようにしましょう。

Point：$\small x=k$上の格子点の個数の求め方

（直線$\small x=k$上の格子点の個数）=（範囲内で最大の$\small y$座標の整数）$\small -$（範囲内で最小の$\small y$座標の整数）$\small +1$

この考え方を用いて直線$\small x=k$上の格子点の個数を求めていきます。

格子点の個数を求めるためには、直線$\small x=k$上での$\small y$の範囲を求める必要がありますが、図形の形から最小値はどこでも$\small y=0$（$\small x$軸上）ですが、最大値は場所によって変わります（下図参照）。そのため$\small k$の値によって場合分けが必要です。

$\small k>0$では最大値は$\small y=-k+3$だが、
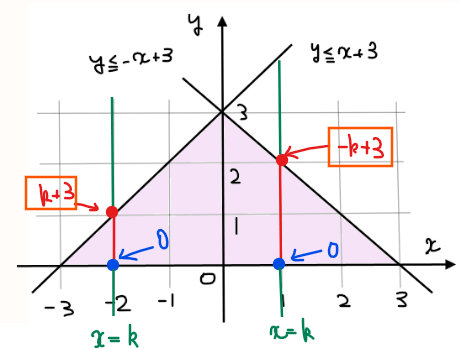
$\small k<0$では最大値は$\small y=k+3$となる

$\small k>0$と$\small k=0$、$\small k<0$の3パターンで場合分けして格子点の数を計算してもよいですが、大変なのでこのような場合は、図形の対称性を利用して計算を楽にできないかを考えるという発想が王道です。

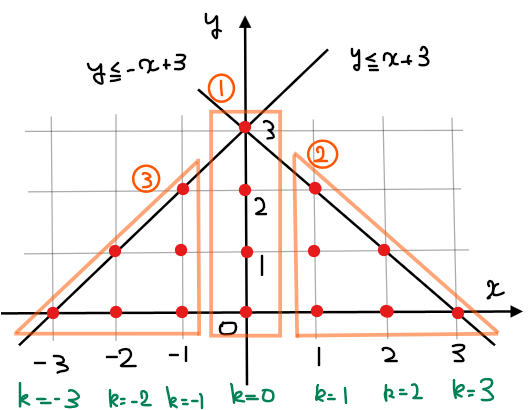
すると、上図のように今回考える図形は直線$\small x=0$を軸に左右対称なので、②の領域（$\small 1≦k≦3$）と③の領域（$\small -3≦k≦-1$）は格子点の個数は同じです。なので③の領域の格子点の個数は求めずに②の領域の個数を2倍すればOKとなり計算がだいぶ楽になります。

ということで、$\small k=0$の場合と$\small 1≦k≦3$の場合の2パターンに場合分けして直線$\small x=k$上の格子点の個数を計算していきます。

(i) $\small k＝0$の場合
図より、直線$\small x=0$上の格子点の個数を求めればOKです。
$\small 0≦y≦3$なので、直線$\small x=0$上の格子点の個数は、$\small 3-0+1=$4個.

(ii) $\small 1≦k≦3$の場合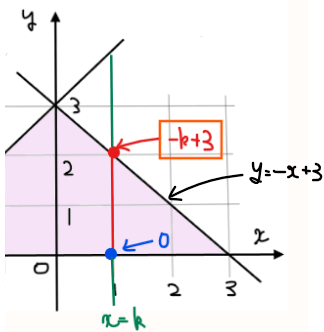

図より、$\small 0≦y≦-k+3$なので、直線$\small x=k$上の格子点の個数は、
\begin{split}
\small (-k+3)-0+1=\color{#ef5350}{-k+4 \space 個}\\
\end{split}

思考のPoint

・$\small y$の範囲が$\small k$の値によって変わる場合は、場合分けで考える
・格子点の数え上げは、図形の対称性を利用できないか考える

STEP

$\small k$の範囲で総数$\small \left(\sum \right)$を計算

領域内の格子点の個数を$\small S$とすると、①の領域（$\small k=0$）内の格子点の個数（$\small S_{0}$とおく）と②の領域（$\small 1≦k≦3$）の格子点の個数（$\small S_{+}$とおく）さえ計算できれば、

\begin{split}
\small S &\small =S_{0}+2S_{+} \space \cdots (*)\\
\end{split}

として求めることができます。

[1] $\small S_{0}$の計算
$\small k=0$、すなわち直線$\small x=0$上での格子点の個数のことなので、これは和をとるまでもなくSTEP1で求めた4個なので、$\small S_{0}=4$。

[2] $\small S_{+}$の計算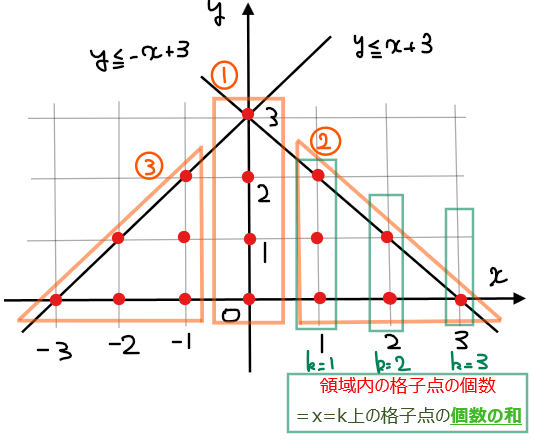

直線$\small x=k$上の格子点の個数 $\small -k+4$を、$\small k=1,2,3$の範囲で和をとればよいので、
\begin{split}
\small S_{+} &\small =\color{#ef5350}{\sum_{k=1}^3(-k+4)}\\
&\small =-\sum_{k=1}^3 k+ \sum_{k=1}^3 4\\
&\small =-\frac{1}{2}\cdot 3 \cdot 4+ 4\cdot 3 \space [*1]\\
&\small =6\\
\end{split}

$\small *1$：$\small \sum$に関する公式
\begin{split}
&\small \sum_{k=1}^n c = cn \space (c：定数)\\
&\small \sum_{k=1}^n k = \frac{1}{2}n(n+1)\\
&\small \sum_{k=1}^n k^2 = \frac{1}{6}n(n+1)(2n+1)\\
&\small \sum_{k=1}^n k^3 = \left\{ \frac{1}{2}n(n+1) \right\}^2\\
\end{split}

よって、$\small S_{0}=4、S_{+}=6$を$\small (*)$に代入することで

\begin{split}
\small S &\small =S_{0}+2S_{+}\\
&\small =4+2\cdot 6\\
&\small =\color{red}{16個 \space \cdots 【答】}\
\end{split}

Point：領域内の格子点の個数の求め方

領域内の格子点の個数は、直線$\small x=k$上の格子点の個数を$\small k$の値の範囲で足し上げで求める。

≪計算式≫
領域内の格子点の個数を$\small S$、直線$\small x=k$上の格子点の個数を$\small S_k$とすると$$\small S= \sum_{k} S_{k}$$※ただしシグマの範囲は$\small k$の範囲によって決まる

【講義3】格子点の個数の求め方

ここでは、格子点の個数を求める問題でよく出てくる考え方について解説します。

例題でも解説した通り、直線$\small x=k$上にある格子点の個数を計算するときには、最大となる$\small y$座標と最小となる$\small y$座標から以下の公式で計算します（ちなみに、直線$\small y=k$上にある格子点の個数であれば、$\small x$と$\small y$の記載を入れ替えてあげればOKです）。

Point：$\small x=k$上の格子点の個数の求め方

（直線$\small x=k$上の格子点の個数）=（範囲内で最大の$\small y$座標の整数）$\small -$（範囲内で最小の$\small y$座標の整数）$\small +1$

この公式で着目してほしい点が2つあります。

1つ目は「＋1」の存在です（単純な引き算じゃない！）。

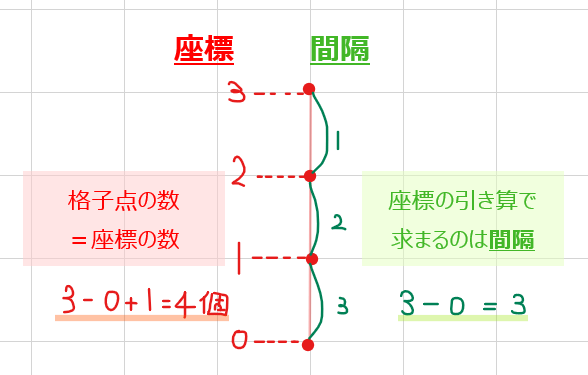
上図のように赤い格子点の個数を求めたい場合は、$\small y$座標の範囲が$\small 0≦y≦3$なので、$\small 3-0=3$個と計算すればよさそうですが、座標の引き算で計算できるのは座標間の長さ（間隔）である点に注意が必要です。

図からもわかる通り、間隔と個数は『個数＝間隔+1』という関係なので、座標間の引き算した結果に『＋1』をする必要があると覚えておきましょう。

そして2つ目は、「範囲内で最大（最小）の整数」の意味についてです。直線$\small x=k$上で取り得る$\small y$の値の範囲の端点がいつも切りよく整数になっているとは限りません。時には、端点の座標が非整数になっていることもあります。そのときの格子点の個数を$\small y$座標の範囲から求めるときには「範囲内で最大（最小）の整数」を見つけてあげる必要があります。

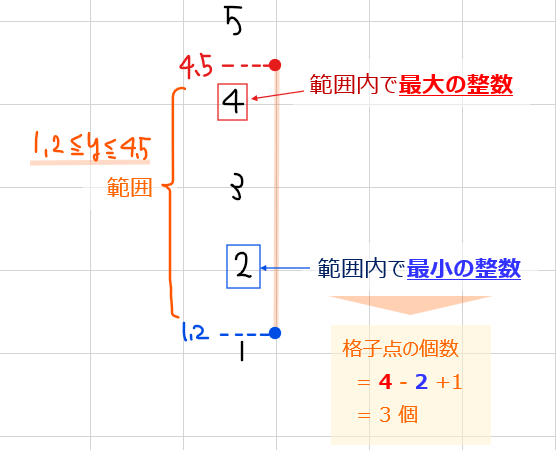
例えば直線 $\small x=k$上で取り得る$\small y$座標の値の範囲が上図のように$\small 1.2≦y≦4.5$であったとします。このとき、 $\small x=k$上の格子点の個数は、もちろん$\small 4.5-1.2+1=4.3$では求まりません。

$\small 1.2≦y≦4.5$の範囲内で最大の$\small y$座標の整数＝4、$\small 1.2≦y≦4.5$の範囲内で最小の$\small y$座標の整数＝2なので、これらの値から$\small 4-2+1=3$個と求める必要があります。

●補足
上記の計算で求めているのは、結局$\small 1.2≦y≦4.5$の範囲内にある$\small y$座標が整数の座標の個数であり、2～4の中に整数が何個あるかというと$\small y=2,3,4$の3個であるということを計算で求めていることになります。

このことからもわかる通り、直線 $\small x=k$上で取り得る$\small y$座標の値の範囲が求まったら、単純に引き算＋1を計算する前に、$\small y$座標の値が整数になっていることも確認するように注意しましょう（【問題2】境界線上に格子点がない場合がこのパターン）。

【講義4】格子点の問題の典型パターン

格子点の問題は大きく2パターンに分けられます。

格子点問題の典型パターン

・パターン①：平面図形/空間図形の領域内の格子点を求める問題
・パターン②：方程式や不等式を満たす整数解を求める問題

パターン①はその名の通りで、格子点の問題と言えば基本は図形的な問題を指します（本記事では平面図形を扱います。空間図形は別記事でまとめる予定ですm(__)m）。

パターン②はパターン①の応用問題で、一見整数問題と見せかけて実は格子点の問題というパターンです。格子点の個数は、簡単に言えば不等式で表される領域内の$\small x,y$座標のうち、$\small x、y$がともに整数のもの個数ですから、代数的な視点から言い換えるならば、『不等式を満たす$\small x,y$の整数解の個数』というわけです。

たとえば簡単な例として、『$\small x+y≦3$を満たす自然数の解を求めよ』という問題があれば、これは、『$\small x+y≦3$、$\small x≧1、y≧1$を満たす格子点の個数を求めよ』という問題と同じになります。

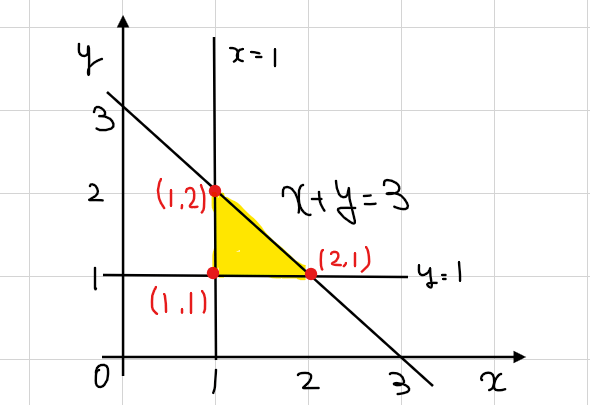
自然数の解、$\small (x,y)=(1,1)、(1,2)、(2,1)$が格子点の座標と一致するわけです。この感覚は非常に大事なのでしっかり理解しておきましょう。

【問題＆解説】格子点に関する問題

【問題1】領域内にある格子点（難易度：★☆☆）

問題1:領域内にある格子点（難易度：★☆☆）

放物線$\small C：y=3x^2-6x$と$\small x$座標が$\small n$（$\small n$は自然数）である放物線$\small C$上の点を$\small \mathrm{P}$、原点を$\small O$とするとき、放物線$\small C$と直線$\small \mathrm{OP}$で囲まれた領域内の格子点の個数を$\small n$の式で表せ。

問題解決のKey

講義2で解説した手順に則り、$\small x=k$上の格子点の数を$\small k$で表したあとに、$\small k=0,1,\cdots,n$の範囲で$\small \sum$を計算する。

　解説

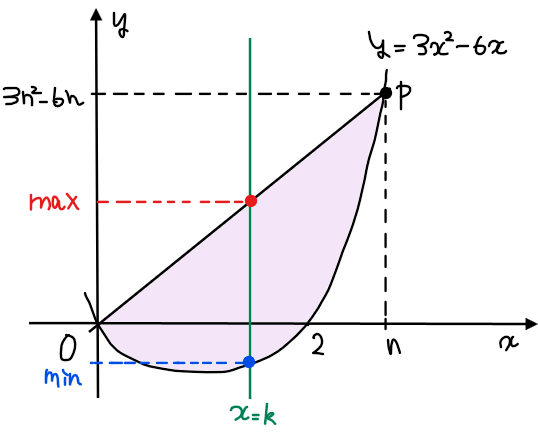
問題文の情報を図示すると上図の通りで、紫色部分が格子点の個数を求める領域。

まずは直線$\small x=k$（$\small 0≦k≦n$）上の格子点の個数を考える。最小値は、放物線$\small C$上の点なので、$\small y_{min}=3k^2-6k$ …①。最大値は、直線$\small \mathrm{OP}$上の点であり、点$\small \mathrm{P}(n,3n^2-6n)$より直線$\small \mathrm{OP}$の式は

\begin{split}
&\small \displaystyle y =\frac{3n^2-6n}{n}x\\
\small \Leftrightarrow \space &\small y=(3n-6)x
\end{split}

この式に$\small x=k$を代入することで、$\small y_{max}=(3n-6)k$ …②。

①、②はともに整数なので$\small [*1]$、直線$\small x=k$上の格子点の個数（$\small S_k$とおく）は、

\begin{split}
\small S_{k} &\small =\color{#5c6bc0}{(3n-6)k}-\color{#ef5350}{(3k^2-6k)}+1\\
&\small =-3k^2+3nk+1\\
\end{split}

$\small *1$：補足
$\small k$や$\small n$は整数なので、それらを足し引きかけ算した$\small 3k^2-6k、(3n-6)k$も当然整数となるから、格子点の個数は単純に座標の引き算+1で求めることができる。
仮に、$\small y_{max}$もしくは$\small y_{min}$が非整数（分数など）の場合は、範囲内で最も大きい整数から最も小さい整数を引き算して+1する必要がある点に注意する（詳細は講義3の解説を参照）。

図から、領域内で取り得る$\small k$の範囲は、$\small k=0,1,\cdots,n$なので、領域内の格子点の総数を$\small S$とすると

\begin{split}
\small S &\small =\sum_{k=0}^n S_{k}\\
&\small =\sum_{k=0}^n (-3k^2+3nk+1)\\
&\small =1+\sum_{\color{red}{k=1}}^n (-3k^2+3nk+1) \space \color{red}{[*2]}\\
&\small =1-3\sum_{k=1}^n k^2+3n\sum_{k=1}^n k+\sum_{k=1}^n 1\\
&\small =1-3\cdot \frac{1}{6}n(n+1)(2n+1)+3n\cdot \frac{1}{2}n(n+1)+n\\
&\small =\frac{2(n+1)-n(n+1)(2n+1)+3n^2(n+1)}{2}\\
&\small =\frac{2-n(2n+1)+3n^2}{2}\times (n+1)\\
&\small =\color{red}{\frac{1}{2}(n+1)(n^2-n+2) \space \cdots【答】}\\
\end{split}

$\small *2$：補足
$\small \sum$の公式は$\small k=1$から$\small k=n$までの和になっているが、今回は$\small k=0$からの和となっているため、このままだと公式が使えない。そこで、$\small k=0$の場合だけ具体的に切り出してあげれば$\small k=1～n$までの和にすることができて公式が使える形になる。
\begin{split}
\small \sum_{k=0}^n a_k &\small =a_0+\color{#ef5350}{a_1+a_2+\cdots +a_n}\\
&\small =a_0+\color{#ef5350}{\sum_{k=1}^n a_k}\\
\end{split}
今回であれば、$\small [*2]$の式では、$\small k=0$の項は、$\small -3k^2+3nk+1$に$\small k=0$を代入すればよいので1となる（ちなみに、この結果は直線$\small x=0$上の格子点の個数は1個という事実とも一致してますね）。

【問題2】境界線上に格子点がない場合（難易度：★★☆）

問題2:境界線上に格子点がない場合（難易度：★★☆）

$\small x≧0$、$\small y≧0$、$\small x+2y≦10$で表される領域内（境界線も含む）にある格子点の個数を求めよ。

問題解決のKey

・$\small x=k$上の格子点の個数を求めようとすると、$\small k$が偶数か奇数かによって式が異なるため、場合分けして求める。
・$\small y=k$上の格子点を考えると境界線（$\small x+2y=10$）上にすべての格子点が乗っかる。切り方を工夫することで場合分けせずに求めることができる（別解参照）。

　解説

例題との大きな相違点は、直線$\small x=k$上の格子点の数を$\small k$を用いて表そうとした際に、$\small k$の値によって計算方法が異なるという点である。

どいうことか説明するために、具体例で考える。

たとえば、直線$\small x=2$上の格子点の個数を考える。$\small x=2$のときの直線$\small \displaystyle x+2y=10 \space \Leftrightarrow \space y=-\frac{1}{2}x+5$の$\small y$座標は

\begin{split}
\small y &\small =-\frac{1}{2}\cdot 2+5\\
&\small =4\\
\end{split}

なので、領域内の$\small y$が取り得る値の範囲としては$\small 0≦y≦4$。

よって、直線$\small x=2$上の格子点の個数は、「格子点の個数の求め方」の公式を用いて計算すると、$\small 4-0+1=5$個と求められる。

では、今度は、直線$\small x=1$上の格子点の個数を考えよう。$\small x=1$のときの直線$\small \displaystyle y=-\frac{1}{2}x+5$の$\small y$座標は

\begin{split}
\small y &\small =-\frac{1}{2}\cdot 1+5\\
&\small =\frac{9}{2}=4.5\\
\end{split}

となり、領域内の$\small y$が取り得る値の範囲としては$\small 0≦y≦4.5$となる。

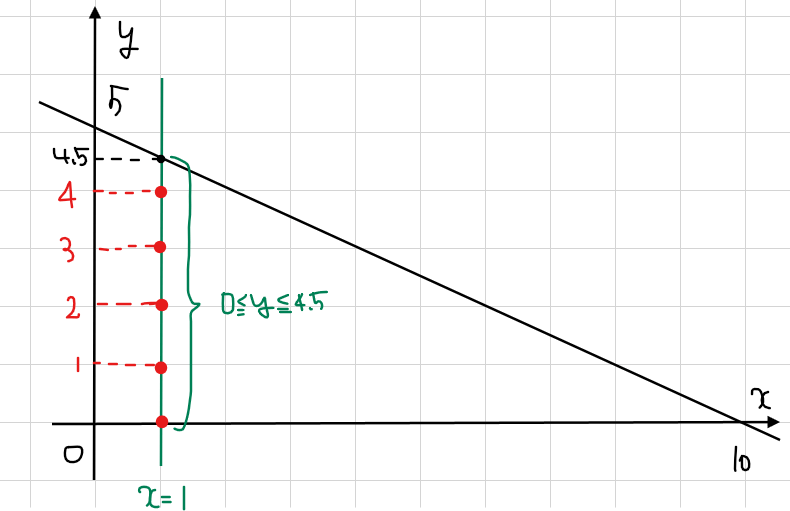
よって、この範囲内にある格子点の数（＝整数となる$\small y$の値）は$\small 0、1、2、3、4$の5つになる。

「格子点の個数の求め方」の公式を用いて計算するならば、$\small 0≦y≦4.5$の範囲内での最大整数である$\small y=4$と、最小整数である$\small y=0$から、$\small 4-0+1=5$と計算することになる。公式であえて「範囲内で最大の$\small y$座標の整数」と記載したのは、本問のように境界線上に格子点が来ない場合があるためである。

このように境界線である$\small \displaystyle y=-\frac{1}{2}x+5$上に格子点が来ない場合があるのは、直線の方程式に$\small \displaystyle -\frac{1}{2}$という非整数が含まれるためであり、$\small \displaystyle -\frac{1}{2}x$が整数になるか否かで$\small y$座標が整数になるか否かが決まる（$\small \displaystyle -\frac{1}{2}x$が整数であれば5を足したものも整数になるので$\small y$の値が整数になる）。

つまり、$\small x=2m(m=0,1,\cdots,5)$（偶数）であれば$\small \displaystyle -\frac{1}{2}x$は

\begin{split}
\small -\frac{1}{2}x &\small =-\frac{1}{2}\cdot (2m)\\
&\small =-m\\
\end{split}

のように整数になり、$\small x=2m-1(m=0,1,\cdots,5)$（奇数）であれば$\small \displaystyle -\frac{1}{2}x$は

\begin{split}
\small -\frac{1}{2}x &\small =-\frac{1}{2}\cdot (2m-1)\\
&\small =-m\color{red}{+\frac{1}{2}}\\
\end{split}

のように非整数になる（下図参照）。

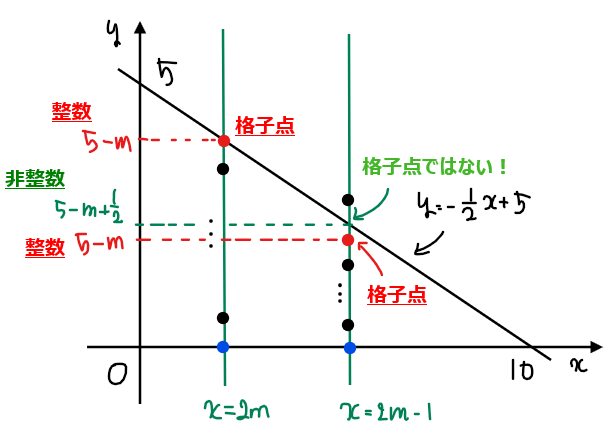
[1]直線$\small x=2m(m=0,1,\cdots,5)$の場合
$\small \displaystyle y=-\frac{1}{2}x+5$に$\small x=2m$を代入すると$\small y=5-m$より、$\small y$座標の取り得る範囲は、$\small 0≦y≦5-m$。
$\small 5-m$は整数なので、直線$\small x=2m$上の格子点の数は、$\small (5-m)-0+1=\color{red}{6-m \cdots ①}$。

[2]直線$\small x=2m-1(m=1,2,\cdots,5)$の場合
$\small \displaystyle y=-\frac{1}{2}x+5$に$\small x=2m-1$を代入すると$\small \displaystyle y=5-m+\frac{1}{2}$より、$\small y$座標の取り得る範囲は、$\small \displaystyle 0≦y≦5-m+\frac{1}{2}$$\small \quad [*1]$。
この不等式を満たす最大の整数は$\small 5-m$なので、直線$\small x=2m-1$上の格子点の数は、$\small (5-m)-0+1=\color{red}{6-m \cdots ②}$。

$\small *1$：補足
$\small \displaystyle y=5-m+\frac{1}{2}$は、$\small \displaystyle y=\frac{11}{2}-m$とさらに計算できるが、格子点の問題では整数部分が大事なので、整数部分と非整数部分が明確になるようにするために、あえて$\small \displaystyle \frac{1}{2}$だけ分離して表記した（$\small 5.5-m$だと整数部分が分かりにくいので、$\small (5-m)+0.5$と表記したイメージ）。

よって、領域内の格子点の個数（$\small S$とおく）は①と②を$\small m$が取り得る範囲内で合計したものになるので

\begin{split}
\small S &\small =\color{red}{\sum_{m=0}^5 (6-m)}+ \sum_{m=1}^5 (6-m) \\
&\small =\color{red}{6+\sum_{m=1}^5 (6-m)}+ \sum_{m=1}^5 (6-m) \quad [*2]\\
&\small =6+2\sum_{m=1}^5 (6-m)\\
&\small =6+2\sum_{m=1}^5 6-2\sum_{m=1}^5 m\\
&\small =6+2\cdot 30 -2 \cdot \frac{1}{2}\cdot 5\cdot 6\\
&\small = \color{red}{36 \space \cdots 【答】}
\end{split}

$\small *2$：補足
$\small \displaystyle \sum_{m=0}^5 (6-m)$を$\small m=0$の項と$\small m=1～5$の項（$\small \displaystyle \sum_{m=1}^5 (6-m)$）に分離している。
$\small m=0$の項は、$\small 6-m$に$\small m=0$を代入すると6と求まる。$\small [*2]$の第2項目と同じ形にまとめるための式変形。

　別解

直線 $\small y=k$（$\small k=0,1,\cdots,5$）上の領域内の格子点の個数を考える。

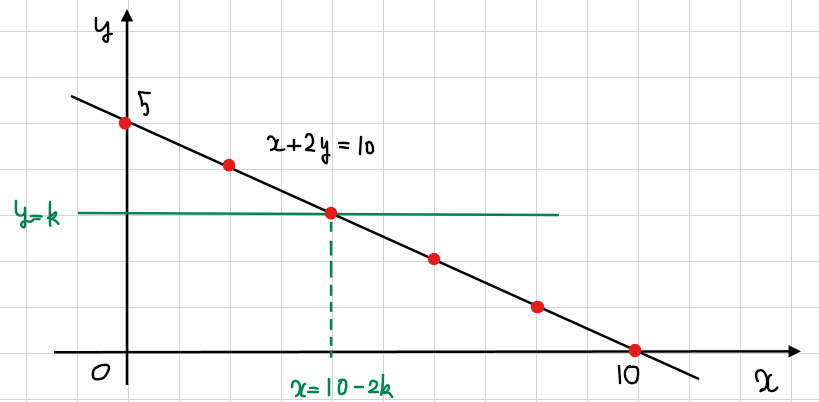
ここで注目してほしいのが、本体の解説では直線 $\small x=k$で領域を縦に切った場合、最大となる格子点が直線$\small x+2y=10$上に乗っかるものと乗っからないものがあり、$\small k$の値で場合分けが必要であったが、上図のように領域を横に切った場合、直線 $\small y=k$上の一番右側の格子点がすべて直線 $\small x+2y=10$上に乗ることが分かる。

つまり、本問の場合は、直線$\small y=k$上の格子点の個数を考える方が場合分けが不要となり簡単に求められるということ。

●補足：縦で切るか横で切るか
直線$\small x=k$と直線$\small y=k$のどちらの格子点の個数を考える方が簡単かは、境界となる式の形からすぐに判断ができる。
本問であれば、直線$\small x+2y=10$は、$\small x=10-2y$となり$\small y$が整数であれば必ず$\small x$も整数になるので、直線 $\small y=k$で考えると$\small x=10-2k$（＝整数）となり$\small x、y$ともに整数になるため格子点の個数を求める計算が楽になる。逆に、直線$\small x=k$で考えると$\small x$は整数になるが、$\small \displaystyle y=-\frac{1}{2}k+5$が分数が含まれてしまうため、整数になる条件で場合分けが必要になり煩雑になる。
つまり、境界となる式で$\small x、y$がともに整数になるような切り方をすればよい。ただし、問題によっては、縦横どちらで切っても整数にならない場合も当然あるので、そのときは場合分けのパターン数が少なくなる方を選ぶとよいだろう。

直線$\small y=k$（$\small k=0,1,\cdots,5$）と直線$\small x+2y=10$の交点の座標は、$\small (10-2k,k)$より、$\small x$座標の取り得る値の範囲は $\small 0≦x≦10-2k$となることから、直線$\small y=k$上の格子点の個数は、

$$\small (10-2k)-0+1=11-2k$$

よって、$\small k=0,1,\cdots,5$の範囲で足し算することで領域内の格子点の個数$\small S$は

\begin{split}
\small S &\small =\sum_{k=0}^5 (11-2k) \\
&\small =11+\sum_{k=1}^5 (11-2k) \\
&\small =11+\sum_{k=1}^5 11-2\sum_{k=1}^5 k\\
&\small =11+55-2\cdot \frac{1}{2}\cdot 5 \cdot 6\\
&\small = \color{red}{36 \space \cdots 【答】}
\end{split}

【問題3】不等式を満たす整数問題（難易度：★★☆）

問題3:不等式を満たす整数問題（難易度：★★☆）

$\small n$を自然数とする。このとき、$\small x+\sqrt{y}≦n$を満たす$\small 0$以上の整数解$\small (x,y)$の個数を$\small n$を用いて表せ。
[中央大改題]

問題解決のKey

・『整数解の個数』＝『格子点の個数』と考える（詳細は、【講義4】格子点の問題の典型パターンを参照）。
・$\small x,y$がともに整数になる方向で切るのが定石。

　解説

本問は、$\small x≧0、y≧0$、$\small x+\sqrt{y}≦n$内の領域にある格子点$\small (x,y)$の個数を求める問題と考えることができる。

直線$\small x=k$上（$\small k=0,1,\cdots,n$）の格子点の個数を考える$\small [*1]$。

$\small *1$：補足
直線 $\small y=k$で切った場合、
\begin{split}
&\small x+\sqrt{k}≦n\\
\small \Leftrightarrow \space &\small x≦n-\sqrt{k}\\
\end{split}
となり、$\small n-\sqrt{k}$は$\small k$の値が平方数（16や81など2乗の数）になっている場合は整数になるが、それ以外の場合は無理数になるため、場合分けがややこしくなり大変。
そのため、本問では$\small x,y$がともに整数になる直線$\small x=k$で考えていくのがよい。

\begin{split}
&\small k+\sqrt{y}≦n\\
\small \Leftrightarrow \space &\small \sqrt{y}≦n-k\\
\small \Leftrightarrow \space &\small y≦(n-k)^2\\
\end{split}

より、$\small y≧0$の範囲と合わせると、直線$\small x=k$上での$\small y$の取り得る値の範囲は $\small 0≦y≦(n-k)^2$なので、直線$\small x=k$上の格子点の個数は、$\small (n-k)^2+1$。

よって、領域内の格子点の個数を$\small S$とおくと

\begin{split}
\small S &\small =\sum_{k=0}^n\{(n-k)^2+1\}\\
&\small =\sum_{k=0}^n (n^2-2nk+k^2+1)\\
&\small =(n^2+1)+\sum_{k=1}^n (n^2-2nk+k^2+1)\\
&\small =(n^2+1)+(n^2+1) \sum_{k=1}^n 1+\sum_{k=1}^n k^2 -2n \sum_{k=1}^n k\\
&\small =(n^2+1)+n(n^2+1)+\frac{1}{6}n(n+1)(2n+1) -2n \cdot \frac{1}{2}n(n+1)\\
&\small =(n^2+1)(n+1)+\frac{1}{6}n(n+1)(2n+1) -n^2(n+1)\\
&\small =\frac{(n+1)}{6} \{ 6(n^2+1)+n(2n+1) -6n^2 \} \\
&\small =\color{red}{\frac{1}{6}(n+1)(2n^2+n+6)\space \cdots【答】}\\
\end{split}

【問題4】方程式と整数問題（難易度：★★★）

問題4:方程式と整数問題（難易度：★★★）

$\small N$を正の整数とする。$\small 2N$以下の正の整数 $\small m,n$からなる組$\small (m,n)$で、方程式 $\small x^2-nx+m=0$が$\small N$以上の実数解を持つようなものは何組あるか。
[東工大]

問題解決のKey

・問題の方程式が所定の条件を満たすような整数の組$\small (m,n)$が何組あるかを求める問題になるので、典型パターン②（講義4）に該当する。
・2次方程式の解の配置問題なので、
　確認Point①：判別式の条件
　確認Point②：軸の範囲
　確認Point③：境界での$\small y$座標
　に着目する（解の配置問題の解き方とパターン別解法については、『2次方程式の解の存在範囲（パターン別解法を徹底解説）』を要チェック！

　解説

本問は、2次方程式$\small x^2-nx+m=0$が$\small N$以上の実数解を持つような整数の組$\small (m,n)$の個数を求める問題であるが、これは$\small mn$平面上で、問題の条件を満たすような領域内にある格子点$\small (m,n)$の個数を求める問題と同じと考えることができる。

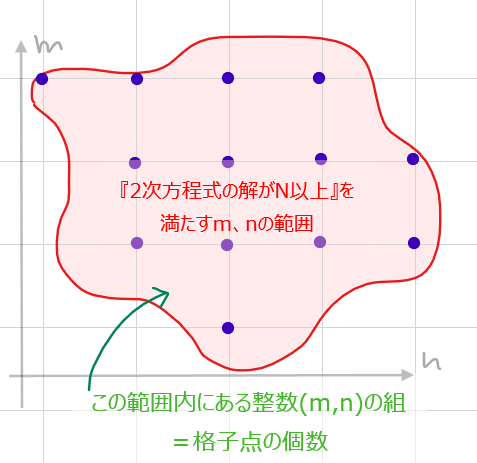
●補足：整数問題→格子点の問題に置き換える考え方
本問は冒頭の通り格子点の問題に置き換えて解くという発想が最も大事なので、もう少しイメージを補足しておく。

『2次方程式$\small x^2-nx+m=0$が$\small N$以上の実数解を持つ』の部分に注目すると、この条件を満たすには$\small n,m$に何かしらの条件があるはずで、何かしらの条件とは簡単に言うと$\small n,m$が満たすべき不等式があるということ（判別式≧0などの不等式が条件になるので）。

$\small n,m$が満たす不等式を$\small nm$平面上にかくと、それは$\small nm$平面上のある範囲を表すことになる。そのため、複数の不等式が$\small n,m$が満たすべき条件（＝不等式）は、図形的には$\small nm$平面上で複数の不等式によって表される領域の共通部分になる。

最後に、『整数の組$\small (m,n)$の個数を求める』の部分に注目すると、これは図形的には$\small nm$平面上の格子点の個数に相当するので、結果として、$\small nm$平面上で条件を満たす不等式が表す領域内の格子点$\small (n,m)$の個数を求める問題に置き換えることができる。

まず問題文より、$\small m,n$は$\small 1≦m≦2N$、$\small 1≦n≦2N$…①を満たす。

ここからは、2次方程式 $\small x^2-nx+m=0$が$\small N$以上の実数解を持つ条件を考える。$\small f(x)=x^2-nx+m=0$とおいて、解の配置問題として考えていこう。

2次関数を図示するために、基礎情報をまとめておくと、軸は$\small \displaystyle x=\frac{n}{2}$であり、①より$\small \displaystyle \frac{1}{2}≦\frac{n}{2}≦N$の範囲にあることが分かる。

つまり、軸は$\small x=N$より左側にあることになるので、このことに注意して$\small N$以上の実数解を持つ場合の2次関数のグラフをかくと下図のようになる。

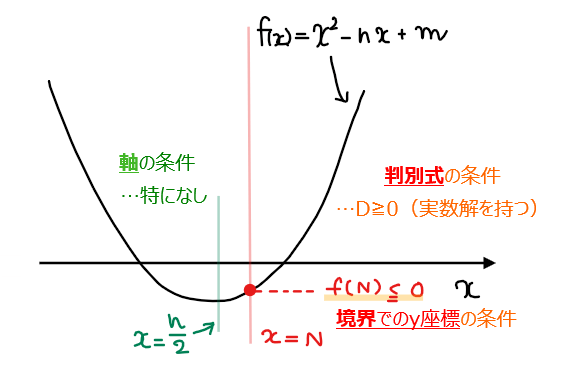
[1] 判別式の条件
実数解を1つ以上でも持っていればよいので、$\small \color{red}{D≧0}$が条件。すなわち、

\begin{split}
\small D =n^2-4\cdot 1\cdot m &\small ≧0\\
\small \Leftrightarrow \space n^2-4m &\small ≧0\\
\small \Leftrightarrow \space \color{red}m &\small \displaystyle \color{red}{≦\frac{n^2}{4} \quad\cdots②}\\
\end{split}

[2] 軸の条件
軸の位置は$\small N$の値によって正にも負にもなり得るし、冒頭の基本情報から

$$\small \frac{n}{2}≦N$$

の位置関係が常に成り立つので、これ以外の追加の条件は特になし。

[3] 境界での$\small y$座標の条件
本問では解の条件が$\small N$以上であることから、$\small x=N$が境界。このときの$\small y$座標に関する条件は、冒頭の図からもわかる通り$\small f(N)≦0$。補足として、$\small f(N)=0$（$\small x$軸上）のときは

\begin{split}
&\small f(N) =0\\
\small \Leftrightarrow \space &\small N^2-nN+m =0\\
\end{split}

より、$\small x=N$が$\small x^2-nx+m=0$の解になるので$\small N$以上の解を持つという条件に合致するため等号も含めてよい。

よって、
\begin{split}
&\small f(N) ≦0\\
\small \Leftrightarrow \space &\small N^2-nN+m ≦0\\
\small \Leftrightarrow \space &\small \color{#ef5350}{m≦Nn-N^2 \space \cdots ③}\\
\end{split}

●補足
$\small N$は定数なので、③は$\small m≦●n+▲$のような直線の下側の領域を表している。

以上の①～③の不等式が表す領域が、『2次方程式$\small x^2-nx+m=0$が$\small N$以上の実数解を持つような整数の組$\small (m,n)$の範囲』になる。不等式が表す領域を$\small nm$平面上に図示する（下図の紫色領域）。

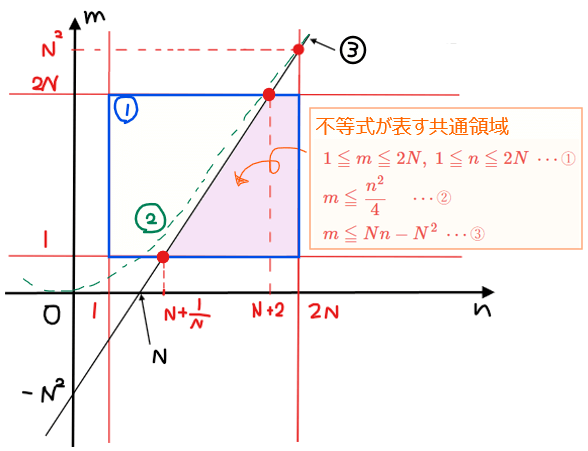
●補足：放物線②と直線③の大小関係
領域を図示する際に気になるのが、放物線②：$\small \displaystyle m=\frac{n^2}{4}$と直線③：$\small m=Nn-N^2$がどこかで交わるのか否かだろう。
『②=③』の関係式を解いて交点の座標を求めておくと
\begin{split}
&\small \displaystyle \frac{n^2}{4} =Nn-N^2\\
\small \Leftrightarrow \space &\small n^2 -4Nn+4N^2=0\\
\small \Leftrightarrow \space &\small (n-2N)^2=0\\
\small ∴\space &\small n=2N\\
\end{split}
よって、点$\small (2N,N^2)$で直線③に接することが分かる。

ここで、直線$\small m=Nn-N^2$について$\small n=2N$のときの$\small m$座標の値は$\small m=N^2$だが、$\small 2N$と$\small N^2$の大小関係について確認しておこう。

上図のように、$\small 2N≦N^2$の大小関係になるには

\begin{split}
&\small 2N≦N^2\\
\small \Leftrightarrow \space &\small N^2-2N≧0\\
\small \Leftrightarrow \space &\small N(N-2)≧0\\
\small ∴ \space &\small N≦0,\space 2≦N\\
\end{split}

$\small N$は正の整数なので、$\small 2≦N$の範囲で上図の大小関係（$\small 2N≦N^2$）が成り立つ。$\small N=1$のときは大小関係が逆転するので最後に別パターンとして考えることにする。

(i) $\small 2≦N$の場合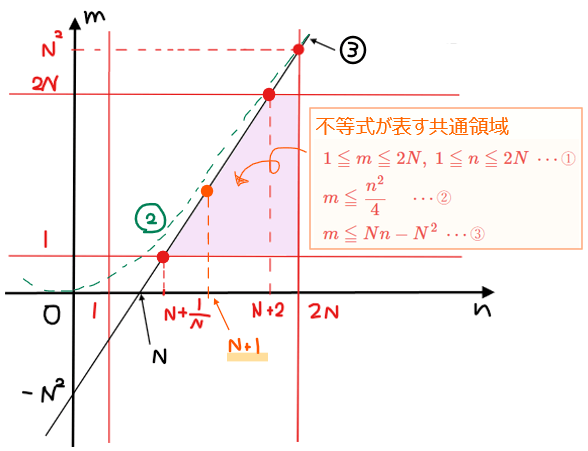

①～③の領域（紫色領域）の左下の点$\small \displaystyle \left(N+\frac{1}{N},1 \right)$を通る直線$\small \displaystyle n=N+\frac{1}{N}$は、$\small \displaystyle N+\frac{1}{N}$の値が非整数でありこの直線上には格子点はないので、その次に$\small n$の値が整数になる直線$\small n=N+1$上での格子点の個数を考える。

直線$\small n=N+1$上の格子点の個数は、領域内の最大値が$\small N$、最小値が$\small 1$なので、$\small N-1+1=N$個…④。

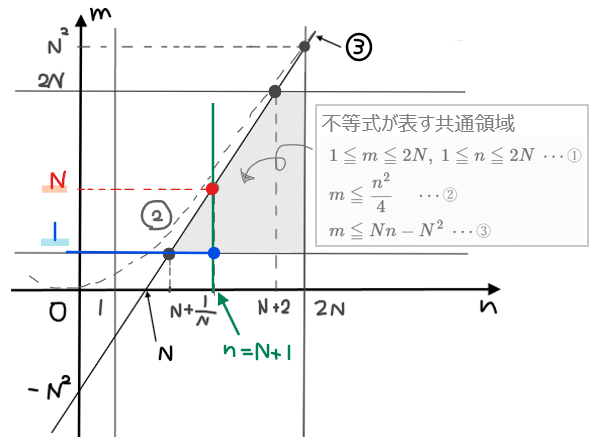
同様に、$\small n=N+2$上の格子点の個数は、領域内の最大値が$\small 2N$、最小値が$\small 1$なので、$\small 2N-1+1=2N$個…⑤。

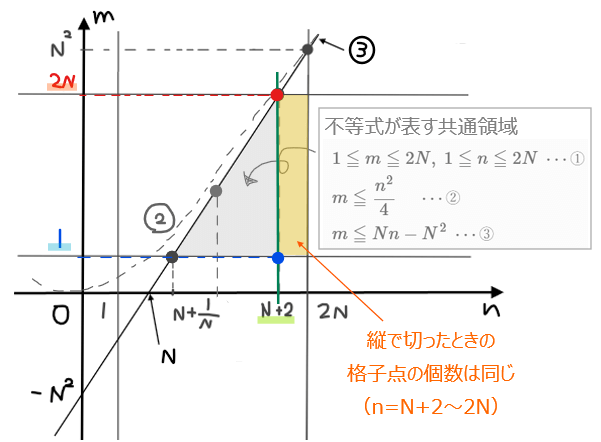
また、$\small n≧N+2$の範囲では、縦で切ったときの直線上の格子点の個数は変わらない（最大値が$\small 2N$、最小値が$\small 1$が変わらない）ので、$\small 2N$個…⑥。

よって、領域内の格子点$\small (n,m)$の個数は、直線 $\small n=N+1$～$\small n=2N$までの各直線上の格子点の総和になるので、④、⑤、⑥から

\begin{split}
&\small N+2N\times \{\color{red}{2N-(N+2)+1}\}\space \cdots \color{red}{[*1]}\\
\small \Leftrightarrow \space &\small =N+2N(N-1)\\
\small \Leftrightarrow \space &\small =\color{#ef5350}{2N^2-N \space \cdots ⑦}\\
\end{split}

$\small *1$：補足
格子点の個数が$\small 2N$個になるような直線（$\small n=■$）の本数は$\small N+2≦n≦2N$の範囲の直線なので、$\small 2N-(N+2)\color{red}{+1}=N+1$本（最後に「＋1」を忘れない）で求めることができる。
文字だとイメージしにくければ、具体的に$\small n=3～6$の範囲で$\small n$の値が整数になるの直線の本数は、$\small 6-3+1=4$本（$\small n=3,4,5,6$）と求められるということ。
あとは『直線の本数×$\small 2N$個』で$\small N+2≦n≦2N$の範囲にある格子点の総数が計算できる。
または、もっとシンプルに長方形領域の格子点の総数なので、縦$\small 2N$個、横$\small N-1$個の格子点の総数として、『縦×横＝$\small 2N(N-1)$個』と求めてもよい。

(ii) $\small N=1$の場合
$\small N=1$の場合に具体的な①～③の領域を図示すると、①～③のすべてを満たす領域は点$\small (2,1)$のみであることが分かる（下図参照）。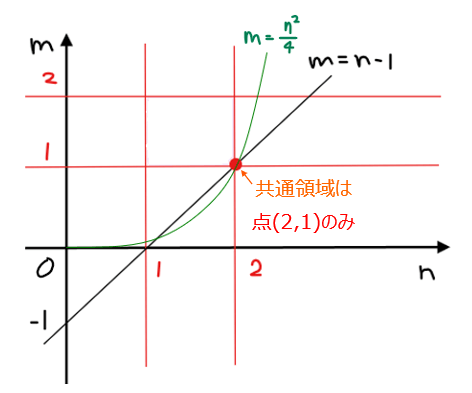

よって、領域内の格子点の個数は1個…⑧。

(i)の⑦、(ii)の⑧より、格子点$\small (n,m)$の個数は

\begin{cases}
\small 2N^2-N \quad (N≧2)\\
\small 1 \quad (N=1)\\
\end{cases}

となるが、$\small 2N^2-N$に$\small N=1$を代入しても1になることから、正の整数 $\small N$に対して問題の条件を満たすような格子点の個数は$\small 2N^2-N$と表せる $\small [*2]$。

$\small *2$：補足
(i)、(ii)で確認したように、$\small N=1$と$\small N≧2$では条件を満たす領域の状況が全く異なるため、一般的に格子点を表す個数の式はそれぞれで異なる。しかし、本問の場合は、たまたま(i)で求めた格子点を表す個数の式（⑦）に$\small N=1$を代入した結果が⑧の結果と一致するため、(i)、(ii)のどちらの場合も共通して$\small 2N^2-N$と表せるということ。
もしも、共通して表せないのであれば、場合分けしたパターンごとの式が答えになる。

よって、『①～③をすべて満たす領域の格子点$\small (n,m)$の個数＝2次方程式$\small x^2-nx+m=0$が$\small N$以上の実数解を持つような整数の組$\small (m,n)$』なので、整数の組も$\small 2N^2-N$…【答】となる。