【数と式】因数分解の基礎問題～応用問題（公式の利用、たすき掛け、対称式、複雑な因数分解）

今回は因数分解の問題を解くときに重要となる考え方の基礎と公式やたすき掛けといったテクニックを利用した解き方、最後には因数分解の総合演習を載せています。

因数分解の問題は、解答を見れば理解できるもののどうやったら解答を見ずに解答のような発想や思考に至れるか？という部分が悩みどころだと思います。でも、実は因数分解をする際にはある程度の考え方のコツがあります。

本記事では、そんな考え方のコツについてわかりやすく解説していきますので、ぜひ最後までチェックしてみてください！

• 因数分解が苦手な人
• 因数分解の解き方のコツを知りたい人
• 因数分解の応用問題が解けるようになりたい人
• 定期テスト対策がしたい人

【問題＆解説】因数分解の基本問題

【問題1】共通因数を利用した因数分解（難易度：★☆☆）

\begin{split}
\small 4x^3y^2+6xy^4 &\small =\color{red}{2xy^2(2x^2+3y^2)\space \cdots【答】}
\end{split}

\begin{split}
\small x^3y-xy^3 &\small =xy(x^2-y^2)\\
&\small =\color{red}{xy(x+y)(x-y)\space \cdots【答】}
\end{split}

【問題2】公式/たすき掛けを利用した因数分解（難易度：★☆☆）

文字 \(\small x\)に注目すると、『2乗+1乗+定数』の形。たすき掛けを利用してもよい\(\small [*1]\)が、\(\small x^2\)の係数は1なので、たすき掛けは省略して普通に因数分解でOK。

\begin{split}
\small x^2+2xy-8y^2 &\small =\color{red}{(x+4y)(x-2y)\space \cdots【答】}\\
\end{split}

\(\small *1\)：たすき掛けを利用した解法
\(\small x^2\)の係数が1の場合は中学でやっていたように感覚的に解く方法でOKだが、たすき掛けを使っても解けることは覚えておこう。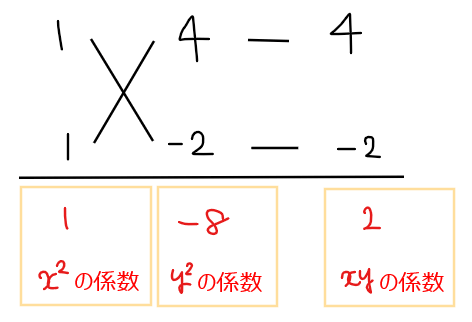

●補足1：因数分解のコツ
因数分解の公式の中で最も典型的な形。以下の3ステップに分けて考えると分かりやすい。

●補足2：複数の文字がある因数分解
\(\small x,y\)の2つ文字が出てきて分かりにくいという人は、初めのうちは\(\small y\)を消して
\begin{split}
\small x^2+2x-8
\end{split}
の因数分解だと考えると分かりやすい。これを因数分解すると\(\small (x-2)(x+4)\)になるので、最後に、\(\small y\)を付けて\(\small (x-2y)(x+4y)\)としてあげれば答えになる。

『2乗+1乗+定数』の形。\(\small x^2\)の係数は1以外なので、たすき掛けを利用する。

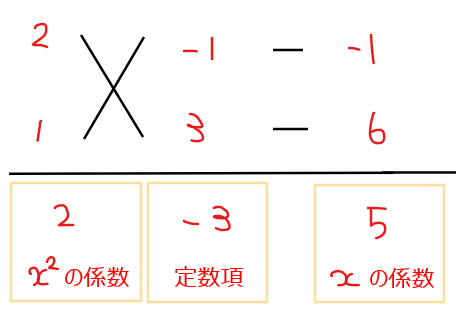
よって、

\begin{split}
\small 2x^2+5x-3=\color{red}{(2x-1)(x+3)\space \cdots【答】}
\end{split}

●補足：因数分解は最後に検算がおすすめ
定期テストなどの試験では、因数分解したら最後に展開して元の式になるかを検算しましょう。検算自体は慣れれば頭の中でぱっとできるので、非常におすすめです。
本問であれば、
\begin{split}
\small (2x-1)(x+3) &\small =2x^2+6x-x-3\\
&\small =2x^2+5x-3\\
\end{split}
となり問題の式と一致することが確かめられます。

\(\small ●x^3+▲y^3\)の形なので、3次式の公式

\begin{split}
\small x^3+y^3=(x+y)(x^2-xy+y^2)
\end{split}

が使えそうです。この公式で\(\small x \to 2x\)、\(\small y \to 3y\)に置き換えると

\begin{split}
\small (2x)^3+(3y)^3 &\small =(2x+3y)((2x)^2-(2x)\cdot(3y)+(3y)^2)\\
&\small = \color{red}{(2x+3y)(4x^2-6xy+9y^2)\space \cdots 【答】}\\
\end{split}

文字\(\small x\)に着目すると、\(\small x^3\)が含まれた3次式なので、

\begin{split}
\small x^3+3x^2y+3xy^2+y^3=(x+y)^3\\
\end{split}

の公式が利用できそうです。問題の式と公式を見比べる\(\small [*1]\)と、\(\small y \to -2y\)に置き換えればよいことが分かります。

\(\small *1\)：見比べるときのコツ
3乗の項の係数に着目すると何に置き換えればよいのかが分かりやすいです。今回であれば、
\begin{split}
\small \color{red}{x^3}-6x^2y+12xy^2\color{red}{-8y^3}\\
\end{split}
の赤字部分に着目すると、\(\small x^3=(x)^3\)、\(\small -8y^3=(-2y)^3\)となるので、\(\small x\)はそのままで\(\small y \to -2y\)に置き換えればよいことが分かります。

実際に置き換えてみると、公式の左辺は

\begin{split}
&\small x^3+3x^2y+3xy^2+y^3\\
\Rightarrow \space &\small x^3+3x^2\cdot \color{red}{(-2y)}+3x \color{red}{(-2y)}^2+ \color{red}{(-2y)}^3\\
&\small =x^3-6x^2y+12xy^2-8y^3\\
\end{split}

となり問題の式を一致する。よって、公式の右辺を\(\small y \to -2y\)に置き換えたものが答えになるので、

\begin{split}
\small x^3-6x^2y+12xy^2-8y^3 = \color{red}{(x-2y)^3 \space \cdots 【答】}\\
\end{split}

【問題3】最低次数の文字で整理する因数分解（難易度：★★☆）

ぱっと見た感じ、共通因数が見当たらず公式やたすき掛けも使えなさそうな形。このような場合は、最低次数の文字について式を整理して解く方針が定石。

本問であれば、最低次数 \(\small b\)について式を整理する。

\begin{split}
&\small a^2+ab-3b-9\\
&\small =(a-3)b+(a^2-9)\\
&\small =\color{#ef5350}{(a-3)}b+\color{#ef5350}{(a-3)}(a+3)\\
&\small =\color{#ef5350}{(a-3)}(b+(a+3)) \quad [*1]\\
&\small =\color{red}{(a-3)(a+b+3)\space \cdots 【答】}
\end{split}

\(\small *1\)：補足
共通因数をくくりだすイメージが湧きづらければ、\(\small a-3=A\)と1つの文字で置いてしまい、
\begin{split}
&\small \color{#ef5350}{(a-3)}b+\color{#ef5350}{(a-3)}(a+3)\\
\Rightarrow \space &\small \color{#ef5350}{A}b+\color{#ef5350}{A}(a+3)\\
&\small =A(b+(a+3))\\
\end{split}
と変形したあとに、\(\small A\)を\(\small a-3\)に戻すと分かりやすい。

●別解
最低次数の文字ではないが、\(\small a\)について整理して解く方法もあるので紹介しておく。
\(\small a\)について降べきの順に整理すると、
\begin{split}
&\small a^2+ba+(-3b-9)\\
&\small =a^2+ba+(-3)\cdot(b+3)\\
\end{split}
\(\small a\)について「2乗+1乗+定数」の形になったので、たすき掛けを利用することで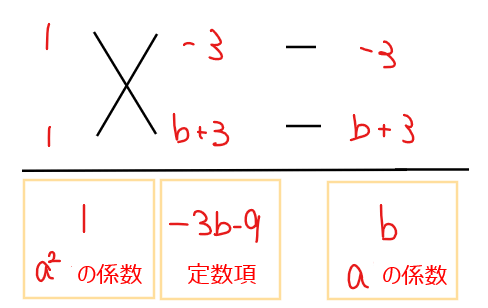

よって、
\begin{split}
\small \color{red}{(a-3)(a+b+3)\space \cdots 【答】}
\end{split}
このように、\(\small a\)の2次式の因数分解になるが、次数が上がるほど因数分解は複雑になるので極力次数が低い式で処理することが望ましい。

（1）同様、公式やたすき掛けが使える形にはないので最低次数の文字について整理する。今回は、\(\small x,y\)どちらを選んでも2次式なので、（どちらでもよいが）ここでは\(\small x\)について整理することにする。

\begin{split}
&\small 3x^2+7xy-x+2y^2+3y-2\\
&\small =3x^2+(7y-1)x+\color{#ef5350}{2y^2+3y-2}\\
&\small =3x^2+(7y-1)x+\color{#ef5350}{(2y-1)(y+2)}\\
\end{split}

\(\small x\)について「2乗+1乗+定数」の形なので、たすき掛けを利用する（下図参照）。

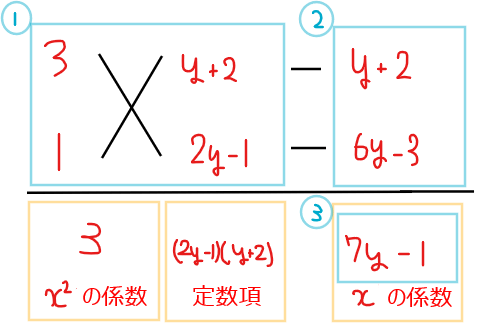
よって、

\begin{split}
&\small \color{red}{(3x+y+2)(x+2y-1)\space \cdots 【答】}
\end{split}

【問題＆解説】因数分解の応用問題

【問題4】対称式の因数分解（難易度：★★☆）

問題の式を

\begin{split}
\small (-a)^2+b^2+c^2+2(-a)\cdot b+2bc+2c \cdot (-a)
\end{split}

とみなすと、\(\small -a,b,c\)に関して対称式（どの2文字を入れ替えても式が変わらない）の因数分解であることが分かる。よって、対称式の関係式を利用して因数分解する方針で考える。

\(\small a^2+b^2\)の形から\(\small (\cdots)^2\)の形に式変形を試みると

\begin{split}
&\small \color{red}{a^2+b^2}+c^2\color{red}{-2ab}+2bc-2ca\\
&\small =\color{red}{(a-b)^2}+c^2+2bc-2ca\\
\end{split}

上式の\(\small (a-b)^2+c^2\)をみて、さらに\(\small (\cdots)^2\)の形に式変形ができないか考えると、\(\small a-b=A\)とひと塊とみなせば、

\begin{split}
&\small (a-b)^2+c^2+2bc-2ca\\
&\small =\color{red}{(a-b)^2}+c^2-2\color{red}{(a-b)}c\\
\small \Rightarrow \space &\small \color{red}A^2+c^2-2\color{red}Ac\\
&\small =(A-c)^2\\
\end{split}

よって、最後に\(\small A=a-b\)に戻せば、\(\small (a-b-c)^2 \space \cdots\)【答】.

●別解
本問は、問題3で触れたように1つの文字について整理する解法でも解くことができる。
\(\small a\)について式を整理すると
\begin{split}
&\small a^2+b^2+c^2-2ab+2bc-2ca\\
&\small =a^2-2ab-2ca+b^2+2bc+c^2\\
&\small =a^2-2(b+c)a+(b+c)^2\\
&\small =(a-(b+c))^2\\
&\small =\color{red}{(a-b-c)^2 \space \cdots【答】}\\
\end{split}

問題の式を

\begin{split}
\small a^3+b^3+(-c)^3-3ab\cdot (-c)
\end{split}

とみなすと、\(\small a,b,-c\)に関して対称式になることから、対称式の関係式を利用して因数分解する方針で考える。

\(\small a^3+b^3\)の部分から、\(\small (\cdots)^3\)の形に変形することを考えると

\begin{split}
&\small a^3+b^3=(a+b)^3-3ab(a+b)
\end{split}

より

\begin{split}
&\small a^3+b^3-c^3+3abc\\
&\small =(a+b)^3-3ab(a+b)-c^3+3abc\\
&\small =\color{red}{(a+b)^3-c^3}-3ab(a+b)+3abc\\
&\small =\color{red}{(a+b-c)^3+3(a+b)c(a+b-c)}-3ab(a+b-c) \space [*1]\\
&\small =(a+b-c)((a+b-c)^2+3(a+b)c-3ab)\quad \color{red}{◀共通因数 (a+b-c)でくくった}\\
&\small =(a+b-c)(a^2+b^2+c^2+2ab-2bc-2ca+3ac+3bc-3ab)\\
&\small =\color{red}{(a+b-c)(a^2+b^2+c^2-ab+bc+ca)\space \cdots【答】}\\
\end{split}

\(\small *1\)：補足
\(\small [*1]\)への赤字部分の式変形は、問題解決のKeyで紹介した『よく使う対称式の関係式』の
$$\small x^3+y^3=(x+y)^3-3xy(x+y)$$
に対して、\(\small y \to -y\)に置き換えた式である
$$\small \color{red}{x^3-y^3=(x-y)^3+3xy(x-y)}$$
を利用している。
実際に、\(\small x=a+b, y=c\)として上記の公式にあてはめると
\begin{split}
\small x^3-y^3 &\small=(x-y)^3+3xy(x-y)\\
\small \Rightarrow \space (a+b)^3-c^3 &\small=((a+b)-c)^3+3(a+b)c((a+b)-c)\\
\end{split}
となり、余計な括弧をはずせば\(\small [*1]\)の形になることが分かる。

●考察
本問で特定の文字について整理する解法で解けないのか考えてみよう。

たとえば、\(\small a\)について式を整理すると、
\begin{split}
&\small a^3+b^3-c^3+3abc\\
&\small =a^3+3bca+b^3-c^3\\
\end{split}
となるが、これは\(\small a^3\)が含まれるため3次式の因数分解であり、3次式公式にも該当しないことからこれ以上うまい変形ができない。

このように、3次式の因数分解は公式を使う以外に一般的な解法がないので、対称式を意識した式変形をしてうまく共通因数を見つけ出す必要がある。

【問題5】工夫が必要な因数分解（難易度：★★☆）

因数分解するためには一度展開する必要があるが、全部を展開するのは大変かつその後の因数分解も大変。そこで、うまく同じ形が出てくるように展開していくことで、計算量を減らしつつ因数分解しやすい形を維持できる。

同じ形を作る際に意識したいことが、ペアリングの仕方である。大きいものと小さいものをペアにして展開してあげるとバランスが取れてうまくいくことが多い。

本問であれば、\(\small (x-4)(x+3)\)と\(\small (x-2)(x+1)\)をペアとして展開すると

\begin{split}
&\small (x-4)(x-2)(x+1)(x+3)+24\\
\small =&\small \color{#ef5350}{(x-4)(x+3)}\color{#5c6bc0}{(x-2)(x+1)}+24\\
\small =&\small \color{#ef5350}{(x^2-x-12)}\color{#5c6bc0}{(x^2-x-2)}+24\\
\end{split}

となり、括弧内に\(\small x^2-x\)という同じ形を作り出すことができた。

ここで、計算のしやすさのため\(\small x^2-x=A\)とおくと、

\begin{split}
&\small (x^2-x-12)(x^2-x-2)+24\\
\small =&\small (A-12)(A-2)+24\\
\small =&\small (A^2-14A+24)+24\\
\small =&\small A^2-14A+48\\
\small =&\small (A-6)(A-8)\\
\end{split}

\(\small A=x^2-x\)を元に戻すと

\begin{split}
&\small (A-6)(A-8)\\
\small =&\small (x^2-x-6)(x^2-x-8)\\
\small =&\small \color{red}{(x-3)(x+2)(x^2-x-8) \space \cdots 【答】}\\
\end{split}

●OnePoint
\(\small A=x^2-x\)に戻した\(\small (x^2-x-6)(x^2-x-8)\)を答えにしてしまうミスが多いので、答えを出した後にさらに因数分解ができないか確認する癖をつけておくとよいでしょう。

文字\(\small a,b\)のどちらに着目しても最低次数が5次式であり、この状態ではたすき掛けや公式を使った因数分解はできないため、同じ形を作り出すことを念頭に置いてペアを考えていこう。

\begin{split}
&\small a^5-a^2b^2(a-b)-b^5\\
\small =&\small a^5-a^3b^2+a^2b^3-b^5\\
\small =&\small a^3\color{#ef5350}{(a^2-b^2)}+b^3\color{#ef5350}{(a^2-b^2)} \space [*1]\\
\small =&\small \color{#ef5350}{(a^2-b^2)}(a^3+b^3)\\
\small =&\small (a+b)(a-b)(a+b)(a^2-ab+b^2)\\
\small =&\small \color{red}{(a+b)^2(a-b)(a^2-ab+b^2)\space \cdots 【答】}\\
\end{split}

\(\small *1\)：OnePoint
ペア（組合せ）を考えるときには、次数の大きいものと小さいものを組み合わせると全体的に同じくらいの次数になり、同じ形が見つかりやすい。

●別解
本問の場合は、以下のようなペアでも同様に共通因数を見つけて解くことができる。
\begin{split}
&\small a^5-a^3b^2+a^2b^3-b^5\\
\small = &\small a^5+a^2b^3-b^5-a^3b^2\\
\small =&\small a^2\color{#ef5350}{(a^3+b^3)}-b^2\color{#ef5350}{(b^3+a^3)}\\
\small =&\small \color{#ef5350}{(a^3+b^3)}(a^2-b^2)\\
\small =&\small \color{red}{(a+b)^2(a-b)(a^2-ab+b^2)\space \cdots 【答】}\\
\end{split}

【問題6】総合問題（難易度：★★★）

ぱっとみ共通因数はなく、式中に括弧なども見当たらないことから、最低次数について整理する方針で考える。\(\small x,y\)どちらも同じ次数（2次式）なので、\(\small x\)について整理すると、

\begin{split}
&\small 2x^2y+2x^2-xy^2-4xy-3x+2y^2-2\\
\small =&\small 2(y+1)x^2-(y^2+4y+3)x+2(y+1)(y-1)\\
\small =&\small 2(y+1)x^2-(y+1)(y+3)x+2(y+1)(y-1)\\
\small =&\small (y+1)(2x^2-(y+3)x+2(y-1)) \quad \color{red}{◀共通因数で括った}\\
\end{split}

となり、後ろ側の括弧の中身が\(\small x\)に関して「2乗＋1乗＋定数」の形なので、たすき掛けを利用して因数分解する（パターンⅡ）。

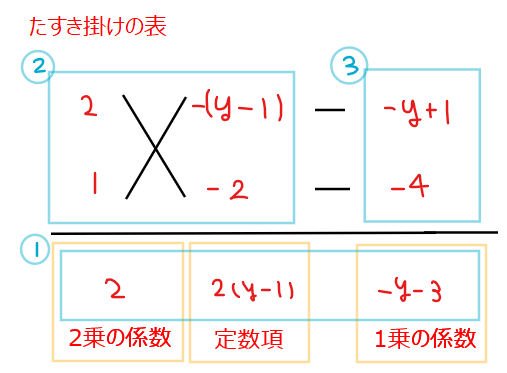
括弧の中身は上記のようにたすき掛けができるので、\(\small (y+1)(2x-y+1)(x-2) \space \cdots\)【答】。

●補足
はじめの式を見ただけでは共通因数がないように見えても、特定の文字について整理していく過程で共通因数が見つかることもある。共通因数があると計算が複雑になるので、できるだけ早めに括ってしまいましょう。
ちなみに、共通因数に気づかずに、\(\small 2(y+1)x^2-(y^2+4y+3)x+2(y+1)(y-1)\)のまま因数分解を続けても解けますがたすき掛けのパターンが多くなり大変になります（下図参照）…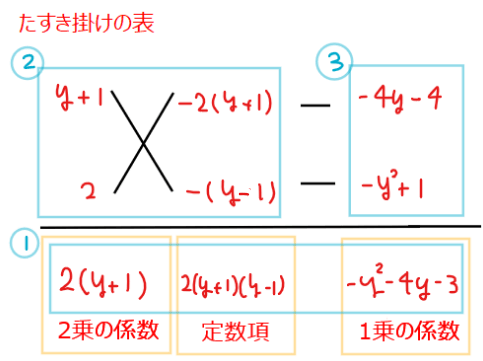

\begin{split}
&\small ((y+1)x-2(y+1))(2x-y+1)\\
\small =&\small (y+1)(x-2)(2x-y+1) \space \cdots 【答】\\
\end{split}

括弧を含んだ複雑な数式であることから、アプローチ③の同じ形を作り出すことを意識した式変形をしていく。とはいえ、いきなり何もない状態から作り出すのは大変なので、まずは\(\small x\)について数式を整理してみる。

\begin{split}
&\small x(y^2-z^2)+y(z^2-x^2)+z(x^2-y^2)\\
\small =&\small (z-y)x^2+(y+z)(y-z)x+yz^2-zy^2\\
\small =&\small (z-y)x^2-(y+z)(z-y)x+yz(z-y)\\
\small =&\small (z-y)(x^2-(y+z)x+yz) \\
\small =&\small (z-y)(x-y)(x-z) \space [*1]\\
\small =&\small \color{red}{(x-y)(y-z)(z-x)\space \cdots 【答】} \space [*2]\\
\end{split}

\(\small *1\)：補足
\(\small x^2-(y+z)x+yz=(x-y)(x-z)\)は因数分解の一番基本的な形。意外と文字で出てくると分かりにくかったかもしれないですね。\(\small x^2\)の係数が1なのでたすき掛けを使うほどの因数分解ではないですが、たすき掛けでも最悪解けます。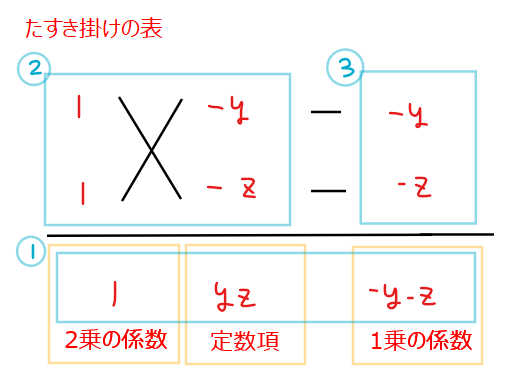

\(\small *2\)：補足
最後の答えは一つ前の\(\small (z-y)(x-y)(x-z)\)でも正解ですが、
\begin{split}
&\small (z-y)(x-y)(x-z)\\
\small =&\small \{\color{red}{-(y-z)}\}(x-y)\{\color{red}{-(z-x)}\}\\
\small =&\small (x-y)(y-z)(z-x)\\
\end{split}
のように2つのマイナスを打ち消すことで、対称性を意識した輪環の順（\(\small x→y→z\)のサイクル）になるように並べ替えしています。このような解答になっていることが多いので一応知っておきましょう。

共通因数も括弧もなく文字も1つのみであり、これ以上式変形のしようがないという点で初見だと手が止まりそうになるが、数式自体は対称式（パターンⅢ）になっている。

\(\small x^4\)を\(\small (x^2)^2\)とみなせば、\(\small ●^2+▲^2\)の形なので、括弧の2乗の形を作ることを考えてみる。

\begin{split}
&\small x^4+4\\
\small =&\small (x^2)^2+2^2\\
\small =&\small (x^2+2)^2-2\cdot x^2 \cdot 2 \quad [*1]\\
\small =&\small (x^2+2)^2-4x^2\\
\small =&\small (x^2+2+2x)(x^2+2-2x)\\
\small =&\small \color{red}{(x^2+2x+2)(x^2-2x+2) \space \cdots 【答】}\\
\end{split}

\(\small *1\)：補足
$$\small a^2+b^2=(a+b)^2-2ab$$
の公式を\(\small a=x^2,b=2\)として利用している。
また、そのあとの式変形は
$$\small a^2-b^2=(a+b)(a-b)$$
の公式を、\(\small a=x^2+2,b=2x\)として利用している。

式中に括弧がある問題なので、うまく式を整理しながら共通因数を探す方針で考える。

式中に出てくる括弧、\(\small b+c,c+a,a+b\)が\(\small a+b+c\)であれば共通因数として括りだせることから、無理やり作りだすと

\begin{split}
&\small a^3+b^3+c^3+a^2(b+c)+b^2(a+c)+c^2(a+b)\\
\small =&\small a^3+b^3+c^3+a^2(b+c\color{red}{+a})\color{red}{-a^3}\\
&\small \quad +b^2(a+c\color{red}{+b})\color{red}{-b^3}+c^2(a+b\color{red}{+c})\color{red}{-c^3}\\
\small =&\small a^2(a+b+c)+b^2(a+b+c)+c^2(a+b+c)\\
\small =&\small \color{red}{(a+b+c)(a^2+b^2+c^2) \space \cdots 【答】}\\
\end{split}

●補足
参考書や教科書などの解説ではスマートな解答だけが記載されるため、まるで閃いたかのように見えてしまい「そんな発想できないよ…」と感じてしまうかもしれないが、実はその解答に至るまでには多くの試行錯誤を行っていることは知っておくとよいだろう（もちろん、問題演習を繰り返すことで試行錯誤の精度が上がり、素早く解法を見つけることはできる）。
私も本問の解答に辿りつくために以下のような試行錯誤をしている。
【試行錯誤その１】
・文字\(\small a\)について整理　→公式が使えない3次式になるのでうまくいかない
【試行錯誤その２】
・対称式なので\(\small a^3+b^3=(a+b)^3-ab(a+b)\)を利用して式変形
　→これもただ式がごちゃごちゃするだけで共通因数が見つからないためうまくいかない
【試行錯誤その３】
・\(\small a^3+b^3+c^3=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)+3abc\)の公式を利用して式変形
　→まぁこれもダメもとで試したけどやっぱりだめ。でも共通因数として\(\small a+b+c\)の形がうまくいのでは？という解答の発想につながった。

【徹底解説】因数分解の攻略法

【講義1】因数分解とは？

唐突ですが、はじめに質問です。因数分解とは何か説明できますか？私が数学の先生だったら定期テストの第1問にこの問題を出すかもしれません（性格悪い…）。

辞書的には、「足し算や引き算が混ざっている式を掛け算の形に変形すること」ですが、これだとよくわからないので、具体的なイメージでかくとPointのようなイメージになります。

つまり、因数分解のゴールは、ごちゃごちゃした式を『括弧がたくさん並んだ状態』にできれば完了というわけです。実際に、教科書や参考書の因数分解の解答欄を開いてみると一目瞭然ですが、どんな答えもきれいに括弧が並んだ形になってませんか？

当たり前のことなのですが、難しい問題になればなるほど式変形しているうちに「あれ、どんな形になったら終わりなんだっけ？」と思う場面に遭遇することが多いので、そんなときは『括弧がたくさん並んだ状態』にすることを思い出してみてください。

【講義2】因数分解の利点

因数分解の解き方の解説に入る前にもう一つだけ、因数分解をする利点を確認しておきましょう。

個人的には、方程式や不等式が解きやすくなるということだと思います。数学の問題では、基本的には何かを求めるために方程式や不等式を解くことになります。ですが、方程式や不等式を解くことは簡単なことではなく、数式をきれいに整理整頓しないと解くことができません。

数式を整理するときに非常に効果的なのが、実は積の形に整理することです。なぜならば、積の形にすることで考えるべきパターンが絞れるからです。

積の形に整理するとパターンが絞れる！
たとえば、
\begin{split}
\small □+△=2
\end{split}
という方程式の解は、□と△が整数だとすると、\(\small □=1、△=1\)や\(\small □=-3、△=4\)など無限にあります。
一方で、
\begin{split}
\small □×△=2
\end{split}
という方程式の解は、□と△が整数だとすると、\(\small □=1、△=2\)、\(\small □=2、△=1\)、\(\small □=-1、△=-2\)、\(\small □=-2、△=-1\)の4パターンしかありません。

このように、かけ算というのは方程式や不等式を解く上で非常に効果を発揮します。

もう一つだけ2次方程式の例を挙げておくと、\(\small x^2+x-2=0\)を解くときには、左辺が足し算・引き算の形では考えにくいので、因数分解して\(\small (x-1)(x+2)=0\)のように積の形にしてあげることで、『かけ算=0』⇔『かけ算のどちらかが0』という関係を利用して、\(\small x-1=0\)または\(\small x+2=0\)の2パターンに解を絞り込むことで答えを求めることができたワケです。

高校数学でも、2次方程式や2次不等式、3次方程式や整数問題などを考える際に因数分解をして積の形に変形することが重要になってくるので、覚えておきましょう。

【講義3】因数分解のコツ

因数分解の問題はいろいろなパターンがあってどうやって考えていけばよいか分からなくなりがちです。ここでは、因数分解するときの考え方について整理しておきましょう。

必ずしも全問題に当てはまるわけではないですが、因数分解をするときには大きく次の3つのアプローチを意識するのがよいでしょう。

まずはじめにアプローチ①で共通因数がないかを確認し、あれば括ってしまいましょう。

次は数式の形を見てアプローチ②と③のどちらで考えるかを判断します。③は括弧を含んだ複雑な式の場合によく使う手法なので、基本的にはアプローチ②の最低次数の文字で数式を整理してみてパターンⅠ～Ⅲのどれに当てはまりそうかを考えていく感じになります。

それぞれのアプローチの判断の仕方は、実際に問題を解きながら感覚をつかむ方が分かりやすいと思うので、それぞれ以下で解説します。

・アプローチ①　→【問題1】共通因数を利用した因数分解
・アプローチ②_パターンⅠ、Ⅱ　→【問題2】公式/たすき掛けを利用した因数分解、【問題3】最低次数の文字で整理する因数分解
・アプローチ②_パターンⅢ　→【問題4】対称式の因数分解
・アプローチ③　→【問題5】工夫が必要な因数分解

そして、上記パターンを含めた演習問題は、【問題6】総合問題で解説していきます。

なお、冒頭にも触れましたがあくまで傾向的に上記のアプローチで考えるとうまくいくという経験則なので全問題に必ず当てはまるわけではない点はご注意ください。問題を解く中でつまずいたときや解き方が思いつかないときに参考にしてもらえると嬉しいです。

パターンⅠ：公式の利用

因数分解でよく使う公式をまとめました。必須で覚えるものと、できれば覚えたいもの、暗記不要なものに分けています。

●暗記必須の公式
\begin{split}
&\small 1. \quad \color{#ef5350}{a^2+2ab+b^2=(a+b)^2}\\
&\small 2. \quad \color{#ef5350}{a^2-b^2=(a+b)(a-b)}\\
&\small 3. \quad \color{#ef5350}{a^3+b^3=(a+b)(a^2-ab+b^2)}\\
&\small 4. \quad \color{#ef5350}{a^3+3a^2b+3ab^2+b^3=(a+b)^3}\\
\end{split}

●できれば覚えたい公式
\begin{split}
&\small 1. \quad \color{#5c6bc0}{a^2+b^2+c^2+2ab+2bc+2ca=(a+b+c)^2}\\
&\small 2. \quad \color{#5c6bc0}{a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-ac-ca)}\\
\end{split}

●暗記不要（導出可能）な公式
\begin{split}
&\small 1. \quad \color{#ef5350}{a^2-2ab+b^2=(a-b)^2}\\
&\small 2. \quad \color{#ef5350}{a^3-b^3=(a-b)(a^2+ab+b^2)}\\
&\small 3. \quad \color{#ef5350}{a^3-3a^2b+3ab^2-b^3=(a-b)^3}\\
\end{split}

ちなみに、暗記不要とした公式は、暗記必須の公式のマイナス符号バージョンですが、これらの公式はすべて\(\small b \to -b\)に置き換えれば導出可能なので暗記しなくてもOKです。

たとえば、\(\small a^3-b^3\)の公式を導出したければ、\(\small a^3+b^3\)の公式から以下のように導けます。

\begin{split}
&\small a^3+b^3=(a+b)(a^2-ab+b^2)\\
\small \Rightarrow \space &\small a^3+(\color{red}{-b})^3=(a+(\color{red}{-b}))(a^2-a\cdot (\color{red}{-b})+(\color{red}{-b})^2)\\
\small \Leftrightarrow \space &\small a^3-b^3=(a-b)(a^2+ab+b^2)\\
\end{split}

この式変形を見て気づいた人も多いかもしれませんが、実はもっと簡単に導くこともできて、結局変わるのは符号の\(\small \pm\)であり、文字\(\small b\)が偶数乗の項は同符号、奇数乗の項は符号が逆転（\(\small \pm\)が逆転）するという性質を使えば簡単です。

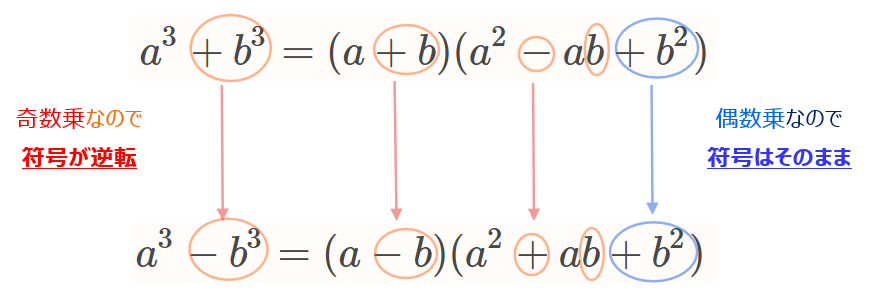
パターンⅡ：たすき掛けの利用

最低次数の文字が複数ある場合に特定の文字で整理した数式が「2乗＋1乗＋定数」の形（2次式の形）になっているときは、たすき掛けを利用します。

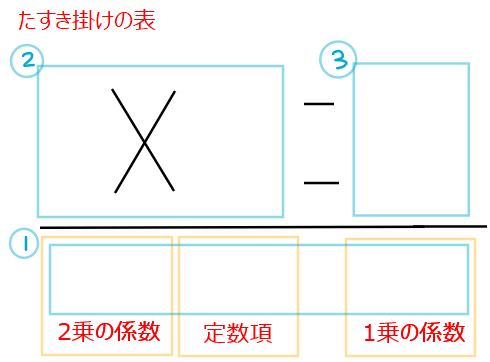
たすき掛けをする際には上記のような表をかいて①→②→③の順で埋めていきます。

例題として\(\small 2x^2-5xy-3y^2\)の因数分解を考えてみましょう。

まず、数式の次数は\(\small x,y\)ともに2次で同じなので、\(\small x\)に関する2次式として整理すると\(\small 2\color{red}{x^2}-5y\color{red}x-3y^2\)となり、「2乗＋1乗＋定数」の形になっているのでたすき掛けで解くことができます。

●補足
\(\small x\)以外の文字（例題だと\(\small y\)や数字）はまとめて数字のようにみなすことで、\(\small -5y\)は\(\small x\)の係数、\(\small -3y^2\)は定数と考えることがポイントです

そうしたら、まずはじめに、2乗の係数、1乗の係数、定数項の枠を埋めます（①）。

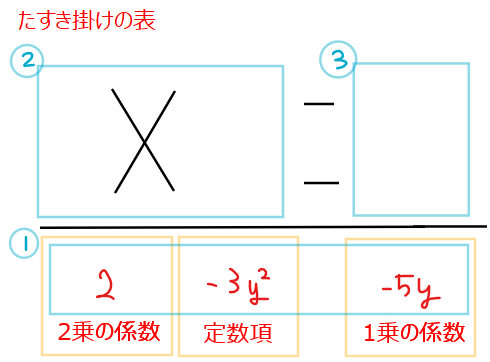
次に①の2乗の係数と定数項を掛け算で分解して②の部分を埋めていき、その計算結果を③に埋めます。このときに③部分の合計が①の1乗の係数と一致するように②はうまく分解します。

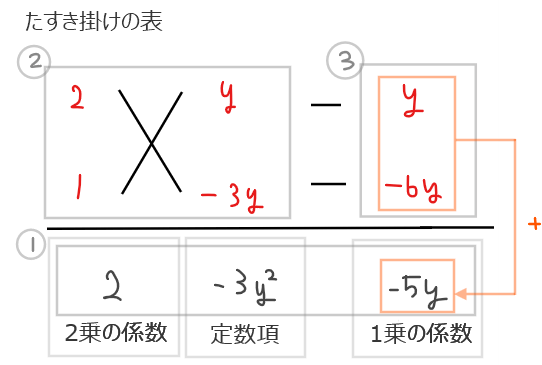
●補足
たとえば、以下のような分解は1乗の係数が\(\small -5y\)にならないので不適。因数分解できる場合は、分解方法は一意に定まるので試行錯誤で探し出しましょう。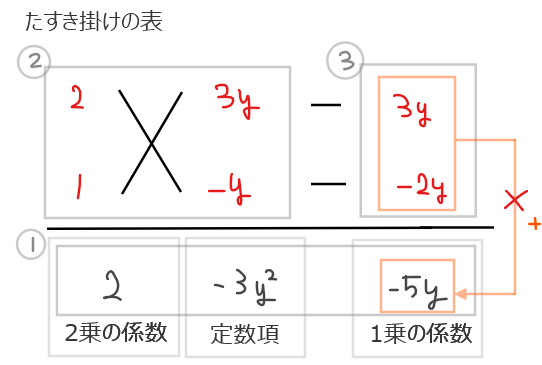

最後は、たすき掛けの表の②の枠内に着目して、「左側が\(\small x\)の係数、右側はそのまま」、「上側と下側で1つの括弧」となるようにしたものが因数分解後の式になります。言葉だと分かりにくいですが、\(\small (2x+y)(x-3y)\)…【答】の形に因数分解できるということです。

パターンⅢ：対称式の関係の利用

対称式の因数分解では対称式の関係を利用する解法がおすすめです。ここで対称式って何？と思った人もいると思うので、まずはそこを解説します。

図形で左右対称といえば、左右を入れ替えても同じ図形になるという性質を表しますが、数式で対称性があるとは、2つの文字を入れ替えても元の式に戻ることを意味するというわけです。

具体例も確認しておきましょう。では、①と②で対称式はどちらでしょう？

\begin{split}
&\small ①：a^2+c^2+ab+c\\
&\small ②：a^2+b^2+c^2+abc
\end{split}

正解は②が対称式です。対称式かどうかを確認するには、適当に2つの文字を入れ替えてみて元の式と一致するかを確認すればよいでしょう。

例えば、①で\(\small a,b\)を入れ替えると、

\begin{split}
&\small b^2+c^2+ba+c\\
\small =&\small b^2+c^2+ab+c\\
\small \neq &\small a^2+c^2+ab+c
\end{split}

となり、元の式とは一致しません。

一方で、②で\(\small a,b\)を入れ替えると、

\begin{split}
&\small b^2+a^2+c^2+bac\\
\small = &\small a^2+b^2+c^2+abc
\end{split}

となり、元の式と一致します。同様に\(\small b,c\)や\(\small c,a\)を入れ替えても元の式に一致することが分かります。よって、②は対称式ということが分かります。

本題に戻って、因数分解する数式が対称式の場合は、対称式の関係式を利用することで因数分解できることが多いです。

実際にどう使うかは、【問題4】対称式の因数分解で確認してみましょう。

本記事のまとめ

今回はいろいろな因数分解を通して因数分解のコツを徹底解説してみました。最後に因数分解の攻略法を復習して終わりにしましょう。

こうしてみると解法がたくさんあって分かりにくいかもしれませんが、個人的にはほとんどの問題は上記アプローチの組合せパターンである「最低次数の文字で整理→公式の利用→共通因数で括る」のステップで解くことができる印象です。ぜひ参考にしてみてください。

では今回は以上です。お疲れさまでした！