今回は、連立1次不等式の解き方を解説していきます。連立1次不等式を解く中で「数直線を使ってどう解くの?」、「共通範囲ってどう考えればいいの?」と悩んでいる人向けに、どう考えて解いていけばよいのか図解を使いながら分かりやすく説明していこうと思います。ぜひ、最後までチェックしてみてください!
1. そもそも連立1次不等式って何?
解き方を説明する前に、そもそも「連立1次不等式」ってどんな式のことを指しているのかについて説明しておきます。一言でいうと、「〇\(\small x\)などの文字と数字しかない大小関係のある式すべてが成り立つ式たち」のことです。ちょっと長くて分かりにくいですよね。連立1次不等式は「連立」、「1次」、「不等式」の3つの言葉が組み合わさっているので、それぞれの言葉に分解してその意味を確認してみましょう。
・1次:式に出てくる文字の最大次数が1乗。
・不等式:大小を表した式。
1つ目の「連立」は、連なって成り立つという意味で、複数の式がすべて成り立つような答えを求める問題のことを意味しています。中学で学ぶ「連立方程式」も、2つの方程式の両方が成り立つような\(\small x\)、\(\small y\)を求めてましたね。片方の式だけが成り立つ解だとそれは適切な解にはならないのと同じです。ちなみに、式の数は2つじゃなくても3つや4つでも「連立」といいます。
2つ目の「1次」は、式中に出てくる文字の最高次数が1乗という意味で、端的にいえば、文字の1乗(〇\(\small x\))or数字しか出てこないということです。
3つ目の「不等式」は、一番わかりやすいと思いますが、その名の通り両辺が等しくない式なので、必ずどちらかに大小関係がつく式のことです。なので式中に必ず不等号が含まれます。
以上をまとめると、冒頭にいった「〇\(\small x\)などの文字と数字しかない大小関係のある式すべてが成り立つ式たち」になります。要は連立方程式の不等式バージョンということなのですが、なぜあえて言葉の意味をはじめに確認したかというと、この意味を理解せずに連立方程式と同じ感覚で解いているとこの後説明する「共通範囲」の考え方がわからないという原因につながるので、少し詳しめに説明しました。
では、次章では言葉の意味を踏まえながら具体的な解き方の基本3stepについて説明してきます!
2. 連立1次不等式の解法3step
ここからは連立1次方程式の解き方を3stepに分けて説明します。これだけ覚えておけば誰でも解けるようになると思うので、一緒に確認していきましょう。
さっそく結論として、解き方は以下の3stepです。
ではそれぞれ説明していきます。
2.1 まずはそれぞれの不等式を解く
連立1次不等式では、基本的には2つ以上の不等式があるので、まずは1つずつの不等式に着目してそれぞれを解いていきます。まれに1つの式で2つ以上の大小関係を表している場合がありますが、そんな時は無理やり2つの不等式に分解してそれぞれを解いていけばokです。

2.2 解の範囲を数直線に図示する
step1でそれぞれの不等式を解いたら\(\small x < 2 \)、\(\small x ≧ -1\)のような解の範囲が求まります。step2では、それぞれの解の範囲を数直線上に図示します。
書き方はとても簡単で、例えば\(\small x < 2 \)、\(\small x ≧ -1\)の場合、以下のように書きましょう。
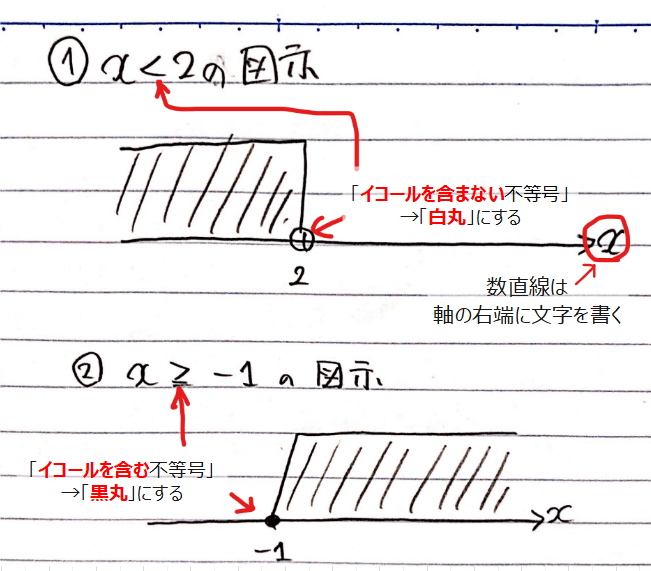
数直線上に解の範囲を描くときに気を付けるべきポイントが2つあります。
1つ目は、軸の右端に文字(今回なら\(\small x \))を書くようにしましょう。高校の不等式問題では文字が複数出てくることはありませんが、大学以降になるとたくさんの文字が出てきて、今書いているのは何の範囲かわからなくなってしまうことがあるので、今のうちから右端には文字を書くクセを付けておきましょう。
2つ目は、境界値が白丸か黒丸かをしっかり分かるように書きましょう。これは高校生でもよくあるミスで、最後の答えにイコールが入る/入らないのミスは、大体が境界値の黒丸/白丸をしっかり書いてないことが原因です。せっかく解いたのに最後の最後でミスするのはもったいなさすぎるので、ミスしないためにも数直線上でしっかり分かるようにしておくことが重要です。
2.3 図示した範囲の共通部分が答え
いよいよ最終ステップです。2.2では説明の都合上つの範囲を分けて記載しましたが、実際には1つの数直線上に書くことで、共通部分が分かるようにします。
今回も\(\small x < 2 \)、\(\small x ≧ -1\)の場合で説明します。同じ数直線上にこれらの範囲を描くと下図のようになります。
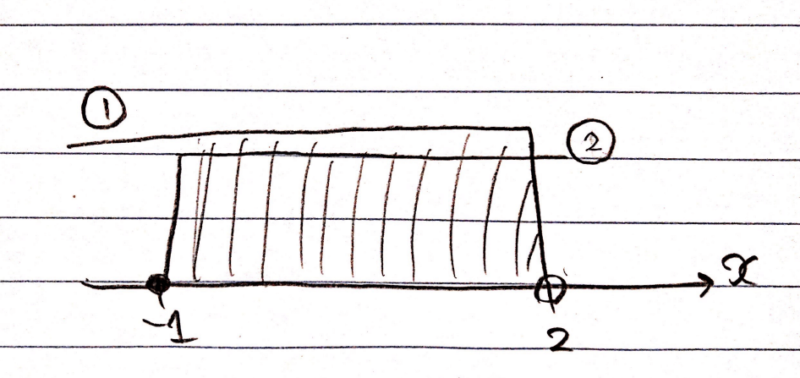
\(\small x < 2 \)を①、\(\small x ≧ -1\)を②とすると①と②の共通範囲は、-1以上2未満の範囲になります。あとは不等式で表すと\(\small -1 ≦ x < 2\)、これが答えになります。
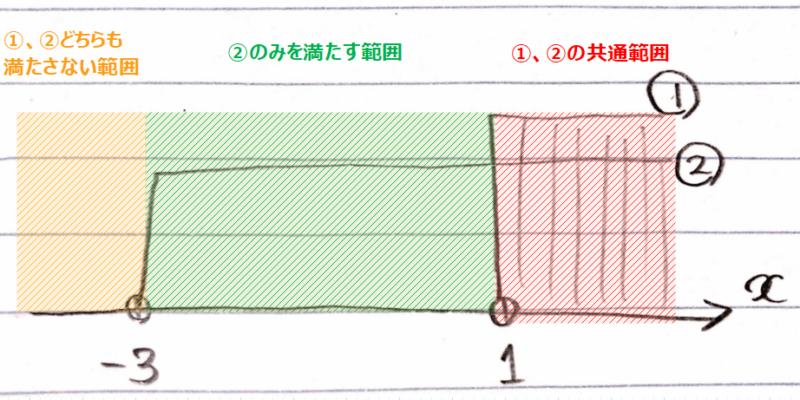
なぜ①と②の共通部分が答えになるかわかりますか?これが初めに「連立1次不等式」の言葉の意味をおさらいしたこととつながります。連立1次不等式は「大小関係のある式すべてが成り立つ式たち」なので①も②もどちらもが成り立っていないといけません。なので、それぞれの範囲の共通部分にある数字であれば、-1以上(②)も満たすし2以下(①)も満たすことができるので、答えになるわけです。もし、下図③の範囲の数字、たとえば-2は、①の2以下は満たしますが、②の-1以上が満たされていないので、答えにはならないわけです。
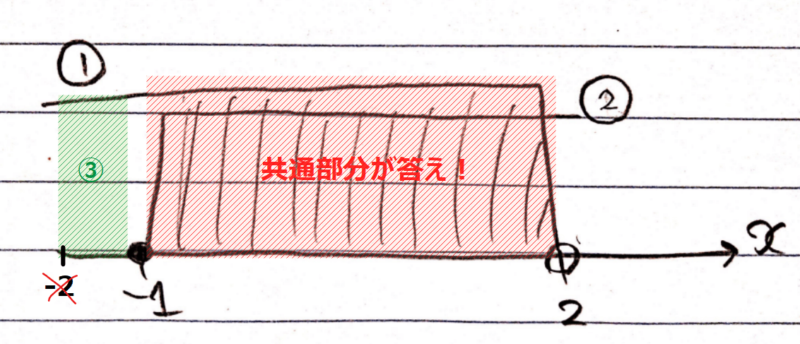
では、具体的な問題を通して連立1次不等式を解いてきましょう。
3. 連立1次不等式を解いてみよう(問題・解説)
3.1 問題1
まずは、step1の通り、1つずつ不等式を解いてきます。
(i)1つ目の不等式
$$4x+2 > 2x+4$$
$$4x-2x > 4-2$$
$$2x > 2$$
$$x > 1 \quad \cdots①$$
(ii)2つ目の不等式
$$5x-1 > 3x-7$$
$$5x-3x > -7+1$$
$$2x > -6$$
$$x > -3 \quad \cdots②$$
それぞれの不等式が解けたので、次はstep2で解の範囲①、②を数直線上に図示していきましょう。
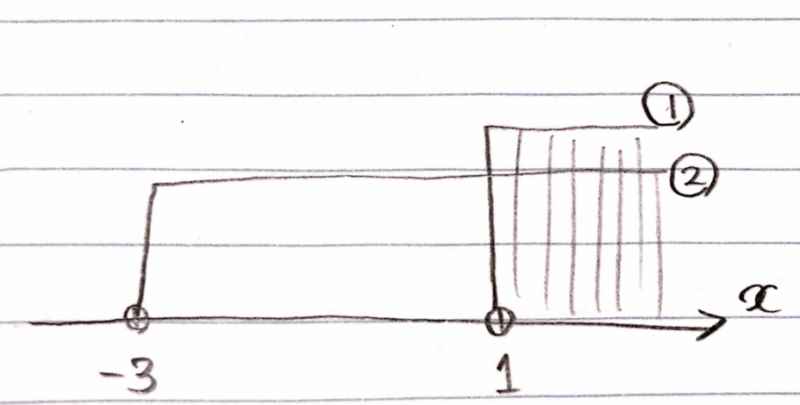
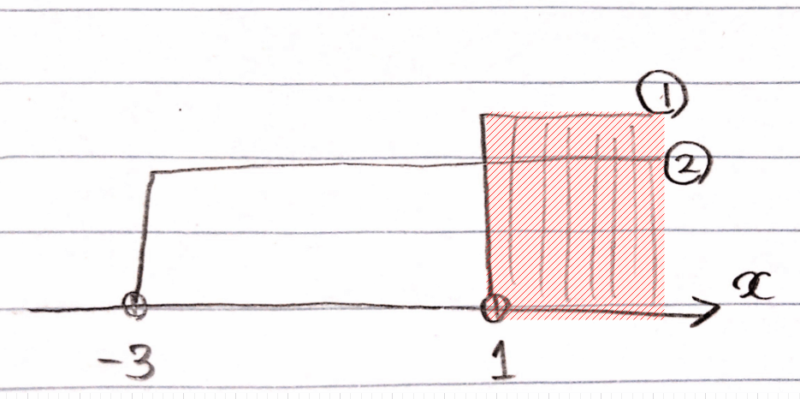
図示できたら、最後は共通部分がどこかを見ていきます。①,②の両方に共通する範囲は以下の赤線部分の範囲なので、答えは、\(\small 1 < x\)となります。
3.2 問題2
それぞれの不等式を解く。
(i) $$5x+3 > 6x+1 $$ $$-x > -2 $$ $$x < 2 \quad \cdots ①$$ (ii) $$3x-4 > x+2$$ $$2x > 6$$ $$x > 3 \quad \cdots ②$$①、②それぞれを数直線で表すとこんな感じ。
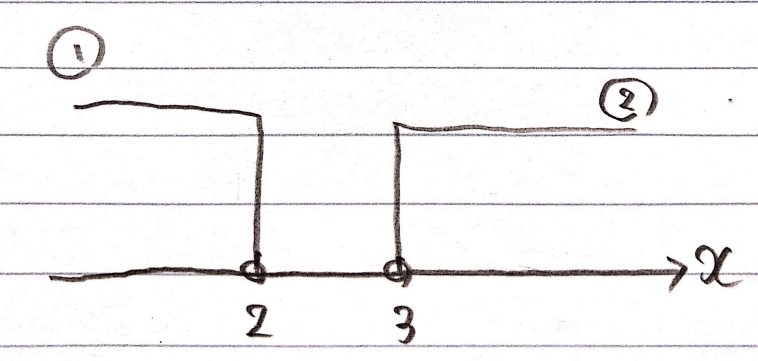
ここでたまに、「答えは①と②を合わせて\(\small x < 2,3 < x\)だ!」としてしまう人が非常に多いのですが、これは不正解なので気を付けましょう。
では、なぜダメなのか理由を説明していきます。step3をもう一度思い出しましょう。「図示した範囲の共通部分が答え」がstep3です。今回の数直線に描いた図で、共通部分はどこでしょうか?答えは共通部分はありません。「え、そんなのずるい…」って思った人もいるかもしれませんが、たまにはこういうパターンもあります。なので、「共通部分が答え」というのをしっかり頭に叩き込んでおきましょう。
よって、答えは解なしとなります。
この問題は、step3で陥りがちなミスとして、「共通範囲を求める」=「出てきた答えを合わせればいい」と勘違いしている人が多かったので、あえて取り上げました。一見どちらも同じように見えますが、数学的には全く違う考え方になるので少し補足しておきます。
「共通範囲を求める」という作業は、複数の条件すべてを同時に満たす範囲になります。全部の条件を満たすことを「AND条件」といいます。ANDは日本語にすると「かつ」という意味です。お部屋探しに例えるなら「家賃が月5万円以下かつ礼金0円」は、家賃が5万円以下じゃないといけないし礼金0円じゃないといけない、これが「AND条件」です。
一方、「出てきた答えを合わせる」という作業は、必ずしもすべての条件を同時に満たさなくてもよい(①は満たすけど、②は満たさないなど)ことになります。いずれかの条件を満たすことを「OR条件」といいます。ORは日本語にすると「または」という意味です。お部屋探しに例えるなら「家賃が月5万円以下または礼金0円」は、家賃が5万円以下じゃなくても礼金0円だったらいいとかその逆など、必ずしも両方の条件を満たさなくてもよい考え方です。
なので、step3の共通範囲を求めることはAND条件を求めることなのに、OR条件で考えてしまうと不正解になってしまうので、これをよい機会に気を付けていきましょう!
3.3 問題3(応用編)
式の数が3つに増えてもやることは同じです。
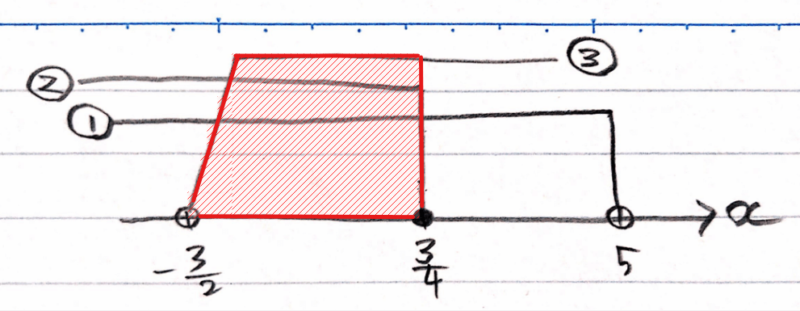
(i) $$3x+4 > 4x-1$$ $$-x > -5$$ $$x < 5\quad \cdots①$$ (ii) $$5x-1 ≦ x+2$$ $$4x≦3$$ $$x≦\frac{3}{4}\quad \cdots②$$ (iii) $$x-1 < 3x+2$$ $$-2x < 3$$ $$x > -\frac{3}{2}\quad\cdots③$$①~③を数直線で図示すると以下のようになります。
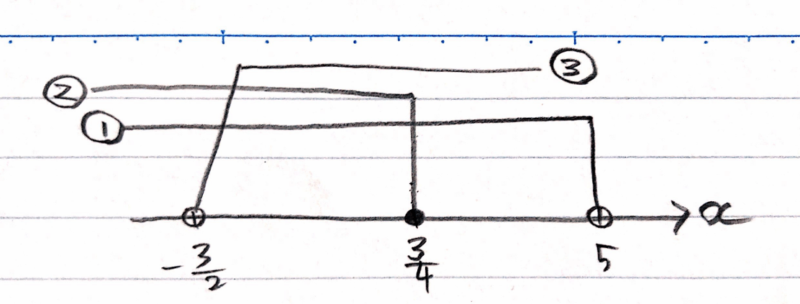
最後は、①~③の共通範囲を探すと\(\small -\frac{3}{2}\)~\(\small \frac{3}{4}\)の範囲だとわかるので、境界値の白丸と黒丸に注意して、答えは、\(\small -\frac{3}{2}<x≦\frac{3}{4}\)になります。
4. まとめ
今回は、連立1次不等式の解き方を3つのstepに分けて説明していきました。
step1では、まずはそれぞれの不等式を解く、step2では、解いた不等式の範囲を数直線に図示する、そして最後のstep3で、すべての範囲に共通する部分が答えになる、この3stepで解くことができるという解説でした。
各ステップの考え方を身に着けることができれば、応用問題でも十分太刀打ちできるはずなので、このレベルは完璧に解けるようになったという人は、もう少しレベルの高い問題に挑戦してみるといろんな学びを得ることができると思います。
では、本日はここまでです。お疲れさまでした!



コメント