この記事では、絶対値を含む方程式の解き方について解説していきます。「絶対値の外し方が分からない…」、「場合分けのやり方が分からない…」、「絶対値を見るだけで解ける気がしない…」などの悩みを抱えている人は、この記事でつまずきポイントを1から10まで徹底解説していますので、ぜひ最後まで確認してみてください！
1. 【はじめに】絶対値を含む方程式が苦手な人が多い理由
解き方を説明する前に、そもそもなんで絶対値を含む方程式（不等式も同じですが）になると解けなくなってしまう人が急増するのか、その理由について私の見解をお伝えします。
結論、「公式に騙されているから」、「解き方を丸暗記しているから」です。ちょっと衝撃的な事実かもしれませんが、それぞれどういうことか説明してきます。
1.1 公式に騙されているから
例えば絶対値を外す公式に以下のような公式があります。
この公式自体はとっても便利な公式なので使うこと自体は全然問題ありません。ただ、便利さゆえに、公式をちゃんと使いこなせてない人が多いなと感じています。
ここで突然ですが質問です。上の公式、皆さんは正確に覚えていますか？「もちろん暗記はばっちりですよ。\(\small |x|=c \quad だったら \quad x=\pm c\)です！」と自信満々に答えた人は要注意。「正確に」というのは、「\(\small c>0\)のとき」という部分までセットで覚えているか？ということです。
この質問をすると、「そこは特に気にしてなかった」とか「あんまり重要そうじゃないし、メインの部分だけとりあえず覚えていれば十分ですよね？」と考えている人が多くいました。
これこそが「公式に騙される」ということです。この分野に限らず、高校で出てくる公式には、「こういう場合は使えますよ」という注意書きがされていることが結構あります。裏を返せば、「条件に当てはまらない場合は使わないでください」ということ。それなのに、注意書きを覚えずにやみくもに公式を使っていると「公式を使ったはずなのに答えが違う…」という悲惨な結果になってしまいます。「このカメラは水中では使わないでください」って書いてあるのに、魚の写真を撮りたくて海水に沈めてしまったら、カメラが壊れてしまうのも当たり前ですよね。
こうならないためにも、公式がどんな場合に使えるかはしっかり把握しておくことが重要になります。
1.2 解き方を丸暗記しているから
2つ目は、解き方を丸暗記しているからです。
こちらも、解き方をある程度覚えておくのは悪くないのですが、考え方を理解せずに「この問題はこう解く」のようなパターンで覚えていると、あとあと絶対忘れます。パターンの数も多いので、「この問題はどっちの解き方で解くんだっけ？」といった事態に陥りやすく、つまずいてしまう要因になってしまいます。
個人的には、「覚える公式は少なく抑え、理解重視で解き進める」方針が数学においては必勝法だと考えているので、このあと、絶対値を含む方程式の基本的な考え方から説明していきたいと思います。
2. 【解説編】絶対値を含む方程式の解法
絶対値を含む方程式は、以下の3stepで解いていきます。
では、それぞれ解説していきます。
2.1 絶対値の中身の正負で場合分けする
絶対値が含まれていると計算ができないので、絶対値を外すのが最初の手順です。絶対値は、中身がプラスであればそのままはずす、中身がマイナスであればマイナスをつけて外す必要があるので、絶対値の中身で場合分けが必要です。
2.1.1 絶対値が1つのみの場合
たとえば、\(\small |x+3|\)の絶対値を外す場合は、絶対値の中身がプラスになる場合、すなわち\(\small x+3 ≧ 0\)→\(\small x ≧ -3\)の場合と、絶対値の中身がマイナスになる場合、すなわち\(\small x+3 < 0\)→\(\small x < -3\)で場合分けします。
上の場合分けで、絶対値の中身がプラスになる場合を\(\small x+3 ≧ 0\)として「イコールを含めた不等号（≧）」で表現して、マイナスの場合を\(\small x+3 < 0\)として「イコールを含めない不等号（<）」で表現しました。
でも、中には「イコールの時って0の時だから、マイナスの場合につけてもいいのでは？」と思った人もいると思うので一応私の見解を述べておきます。
結論、「どちらにつけても数学的には変わらないが、個人的にはプラスの場合に0は含める」、これが私の見解です。
理由は、絶対値を外す作業をするときに、中身がマイナスの場合はマイナスをつけて外すので、\(\small |x+3|=-(x+3)=-x-3\)のような式変形になりますが、中身が0の時ってわざわざマイナスを掛け算して絶対値を外したりしないからです。
なので、本記事では、0の場合はプラス扱いに含めておきます。
2.1.2 絶対値が2つ以上ある場合
方程式の中に絶対値が2つ以上ある場合でも、絶対値の中身がプラスかマイナスかで場合分けして解いていくのは同じですが、場合分けのパターンが少し複雑になります。
結論、場合分けは絶対値の中身が0になる部分で分ければいいです。
たとえば、\(\small |x+3|+|x-1|\)の絶対値を外す場合を考えてみます。まずは、それぞれの絶対値の中身がプラスになるときとマイナスになるときの\(\small x\)の範囲を考えます。
以下の通り図表で整理してみました。
このように、それぞれ数直線上に範囲を図示してみると、絶対値の中身が0になる部分で、状況が変化しています。上図のように青枠aの範囲では、\(\small |x+3|\)、\(\small |x-1|\)の中身はどちらも負、紫枠bの範囲では、\(\small |x+3|\)の中身は正、\(\small |x-1|\)の中身がは負、赤枠cの範囲では、中身は両方とも正になります。
つまり、場合分けとしては、\(\small x<-3\)(青枠a)、\(\small -3≦x<1\)(紫枠b)、\(\small 1≦x\)(赤枠c)の3パターンに分かれることになります。
毎回この図を描くのは大変なので、結論、場合分けは絶対値の中身が0になる部分で分ければいいと覚えておきましょう。
2.2 方程式を解く
step1で場合分けできたら、それぞの場合で絶対値を外して方程式を解いていきます。絶対値さえ外せれば、方程式自体は中学レベルの方程式なので、詳細の解法は割愛します。
2.3 解を吟味する
最後は、解の吟味です。
解の吟味とは、数学用語で「出てきた解が適切なのかを確かめること」です。方程式などを解いて出てきた答えは、状況によって必ずしも正しいとは限りません。
どういうことかというと、例えば、\(\small x^2=1 (x>0)\)という問題では、方程式自体の解は\(\small x= \pm 1\)ですが、条件\(\small x>0\)を考慮すると\(\small x＝-1\)はマイナスですから不適切な解となります。
このように、出てきた解のうち、前提条件を踏まえて本当に出てきた解が適切なのかを確かめる作業、これが解の吟味になります。
これまでは「方程式が解ければそれが答え！」が当たり前だったので、解の吟味は非常に忘れられがちです。でも、今回みたいに「場合分けして解いている場合」などは、今考えているパターンに当てはまっているかを気にする必要があるので、忘れずに解の吟味でチェックしてあげましょう。
3. 【演習編】絶対値を含む方程式を解いてみよう
ここからは、3stepを使用して実際の問題を解いていきましょう。
3.1 基本問題
絶対値があると計算が進まないので、まずは、場合分けをして絶対値を外します。
場合分けは、絶対値の中身が0になる部分で分けるんでした。今回だと、\(\small |x+2|\)の中身である\(\small x+2=0\)となるとき、すなわち\(\small x=-2\)が場合分けの境目になります。\(\small x\)が-2より大きいと、\(\small |x+2|\)の中身はプラスになります。すぐにわからない人は、具体的に-2よりも大きい値をなんでもいいので\(\small x \)に代入してみましょう（たとえば0とかを代入）。必ずプラスになります。逆に、\(\small x \)に-2よりも小さい数を代入すると、\(\small |x+2|\)の中身はマイナスになります。
これで、\(\small x ≧2\)のとき絶対値の中身が正、\(\small x < -2\)のとき絶対値の中身が負であることが分かったので、あとはぞれぞれの場合で方程式を解くだけです。
(i)\(\small x≧-2\)の場合（絶対値の中身が正の場合）$$x+2=2x$$ $$-x=-2$$ $$x=2$$ これは、\(\small x≧-2\)を満たすので解としても適切\(\small \cdots \)①
(ii)\(\small x<-2\)の場合（絶対値の中身が負の場合）
$$-(x+2)=2x$$ $$-x-2=2x$$ $$-3x=2$$ $$x=-\frac{2}{3}$$ これは、\(\small x<-2\)を満たさない（\(\small -\frac{2}{3}=-0.6666\dots \)）ので解として不適切\(\small \cdots\)②
よって①、②より、方程式の解は\(\small x=2\)。
公式、\(\small |x|=c → x= \pm c\)を使って、\(\small |x+2|=2x → x+2= \pm 2x \)で解くのはダメなのでしょうか。答えはNo。公式を正しく使えば答えが出てきます。
「公式に騙されるな」でも説明した通り、この公式には「\(\small c>0\)のとき」という注意書きがありました。今回でいうと、「\(\small 2x > 0 \)の時」で考えれば、正しい答えが出てきます。
\(\small 2x > 0 \)とはすなわち\(\small x > 0 \)なので、この条件に当てはまるか解の吟味をすればよいのです。\(\small x+2= \pm 2x \)を解くと、\(\small x=2、-\frac{2}{3} \)が出てくるので、\(\small x > 0 \)に合致している\(\small x=2\)のみが答えになります。
ただし、この公式は方程式中に絶対値が1つしかない場合でしか使うことができないので、この後出てくる絶対値が2個以降含まれている場合は、今回説明した3stepに沿って解く必要があります。問題によって解き方が違うと混乱したり忘れたりしてしまうので、シンプルに考えるという意味においては、個人的には公式は使わずに解くのがよいと思います。
3.2 応用問題
場合分けのパターンを考えます。絶対値の中身をると、\(\small x=-1、2\)の部分で場合分けが必要です。\(\small x=-1、2\)の2か所で区切れるので、全体としては3つのパターンに場合分けすることになります。
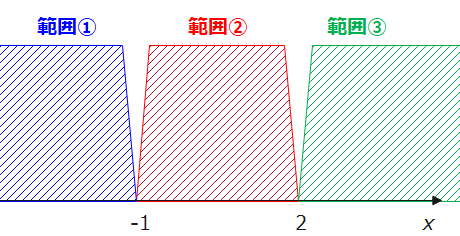
範囲①～③のそれぞれで、絶対値の中身の正負を確認しておきます。
範囲①は、例えば\(\small x=-10\)で考えると\(\small |x+1|<0、|3x-6|<0\)でどちらもマイナスパターンです。範囲②は、例えば\(\small x=0\)で考えると\(\small |x+1|>0、|3x-6|<0\)になります。範囲③は、例えば\(\small x=10\)で考えると\(\small |x+1|>0、|3x-6|>0\)でどちらもプラスパターンです。
では、それぞれのパターンごとに方程式を解いて解の吟味をしていきます。
(i)\(\small x<-1\)の場合$$-2(x+1)+(3x-6)=2x$$ $$-2x-2+3x-6=2x$$ $$x-8=2x$$ $$-x=8$$ $$x=-8$$ \(\small x<-1\)の範囲を考えているため、解としても適切\(\small \cdots\)①。
(ii)\(\small -1≦x<2\)の場合
$$2(x+1)+(3x-6)=2x$$ $$2x+2+3x-6=2x$$ $$5x-4=2x$$ $$3x=4$$ $$x=\frac{4}{3}$$ \(\small -1≦x<2\)の範囲を考えているため、解としても適切\(\small \cdots\)②。
(iii)\(\small 2≦x \)の場合
$$2(x+1)-(3x-6)=2x$$ $$2x+2-3x+6=2x$$ $$-x+8=2x$$ $$-3x=-8$$ $$x=\frac{8}{3}$$ \(\small 2≦x \)の範囲を考えているため、解としても適切\(\small \cdots\)③。
よって、①～③より、方程式の解は\(\small x= -8、\frac{4}{3}、\frac{8}{3}\)。
4. まとめ
今回は絶対値を含む方程式の解き方を解説しました。今まで公式頼みで解いていた人が一人でも多く今回の解き方3stepをマスターして、なんだこんな簡単な考え方だったのかと気が付いていただけたら幸いです。
絶対値を含む方程式に関連して、絶対値を含む1次不等式の解き方については「絶対値を含む不等式の解法」にて解説しているので、苦手な人はぜひチェックしてみてください！
コメント