Σ(シグマ)を使った数列の和の計算は、高校数学でつまずきやすい分野の一つです。
特に、
- Σの和の求め方がそもそも分からない
- 公式を使った後の分数をどのようにくくればいいのか迷う
- 和の途中が打ち消し合う(中抜け)問題の求め方・考え方が分からない
- Σ(シグマ)の和の範囲がk=1~n ではなく、k=2~n−1 などの場合の求め方が分からない
といった悩みを持つ方は多いのではないでしょうか。
この記事では、Σ(シグマ)の基本的な和の求め方から、分数の式のくくり方、和の中抜けの考え方、さらに k=1~n までの和ではない場合(n−1 までの和など)の計算方法まで、例題を交えながら分かりやすく解説します。公式を丸暗記するのではなく、「なぜそう計算できるのか」が理解できるようになることを目標にしています。
Σの計算が苦手な方や、定期テスト・入試対策で確実に得点したい方は、ぜひ最後まで読んでみてください!
- Σ公式を使った後に答えの形にまとめるときの分数のくくり方(まとめ方)のコツを知りたい人
- Σ(シグマ)の和の求め方や「k=1~nでない場合の和」、「和の中抜け」に苦手意識を持っている人
- 定期テスト・共通テスト・大学入試対策としてΣ(シグマ)の典型問題の解き方を理解したい人
Σ(シグマ)の和の求め方|典型問題を徹底解説
【基礎問題】公式を用いたΣ(シグマ)の和|くくり方
次の和を求めよ。
(1)\(\small \displaystyle \sum_{k=1}^n (2k^2+k-1)\)
(2)\(\small \displaystyle \sum_{k=1}^{n} 5\cdot 2^{k}\)
・分配法則を利用して公式を適用せよ!
【等比数列のΣ(シグマ)計算】
・指数部分のズレは積を分解して調整せよ!
【分数のくくり方(まとめ方)のコツ】
・Σ(シグマ)の計算結果をまとめる際のくくり方は以下2点を意識しましょう。
└コツ①:分母は通分する。
└コツ②:分子は共通因数で括る。
【補足】
基礎問題ではシグマに関する公式を利用します。
シグマに関する公式について詳しく理解したい人は、『【数列】Σ(シグマ)記号の意味と公式の覚え方について分かりやすく解説|計算のコツ・和の公式との違い』をチェックしてみましょう!
分配法則を用いて各項ごとにΣを分解すると、
\begin{split}
\small \sum_{k=1}^n(2k^2+k-1) &\small =2\sum_{k=1}^n k^2 +\sum_{k=1}^n k – \sum_{k=1}^n 1 \space \color{#ef5350}{◀分配法則}\\
&\small =2 \cdot \frac{1}{6}n(n+1)(2n+1) +\frac{1}{2}n(n+1)\\
&\small \quad -n\cdot 1 \space \color{#ef5350}{◀公式③,②,①の利用}\\
&\small =\frac{1}{3}n(n+1)(2n+1) +\frac{1}{2}n(n+1)-n\\
\end{split}
あとは計算するだけですが、Σの計算では大体、公式をあてはめた後の式が分数になるため、分数の式を一つにまとめる作業が結構大変で、苦戦している人も多いでしょう。そこで、是非意識してほしいのが、問題解決のKeyにも記載した2つのポイントです。
・コツ②:分子は共通因数で括る。
まず、与式を通分すると
\begin{split}
&\small \frac{1}{3}n(n+1)(2n+1) +\frac{1}{2}n(n+1)-n\\
&\small =\frac{\color{#ff0055}2n(n+1)(2n+1)+\color{#ff0055}3n(n+1)-\color{#ff0055}6n}{6}\\
\end{split}
次に、分子を共通因数 \(\small n\)で括ると
\begin{split}
&\small (与式)=\frac{\color{#ff0055}n\{2(n+1)(2n+1)+3(n+1)-6\}}{6}\\
\end{split}
ここまで来たらあとは括弧の中身を展開して一つにまとめれば完成です。
\begin{split}
&\small \frac{n\{2(n+1)(2n+1)+3(n+1)-6\}}{6}\\
&\small =\frac{n\{2(2n^2+3n+1)+3n+3-6\}}{6}\\
&\small =\frac{n(4n^2+6n+2+3n+3-6)}{6}\\
&\small =\color{red}{\frac{1}{6}n(4n^2+9n-1) \space \cdots 【答】}\\
\end{split}
\begin{split}
&\small \sum_{k=1}^n 5 \cdot 2^k= 5\sum_{k=1}^n 2^k \space \cdots ①\\
\end{split}
のように定数部分は外だしすると、等比数列のΣ公式
$$\small \sum_{k=1}^n r^{k-1}=\frac{r^n-1}{r-1}$$
が使えそうです。
ですが、\(\small r=2\)として上記の公式に適用しようとすると、左辺は
$$\small \sum_{k=1}^n 2^{k-1}$$
となり①の \(\small \displaystyle \sum_{k=1}^n 2^k\)と比較して指数部分が若干ズレていることに気づきます。
このままだと公式が使えないのですが、指数法則を利用して一工夫すると実は公式が使える形に変形ができます。\(\small 2^k = 2 \times 2^{k-1}\)(2の\(\small k\)個のかけ算は2が1個のかけ算と2が\(\small k-1\)個のかけ算に分解できる)であることを用いると、①は
\begin{split}
\small 5\sum_{k=1}^n 2^k &\small =5 \sum_{k=1}^n \color{#ff0055}{2\cdot 2^{k-1}}\\
&\small =5 \cdot 2 \sum_{k=1}^n 2^{k-1}\\
&\small =10 \times \frac{2^n-1}{2-1} \space \color{#ef5350}{◀等比数列の和の公式}\\
&\small =\color{red}{10(2^n-1) \space \cdots 【答】}
\end{split}
【標準問題】k=1~nではないΣ(シグマ)の和
次の和を求めよ。ただし、\(\small a\)は定数とする。
(1)\(\small \displaystyle \sum_{i=1}^{n-2} i^3\)
(2)\(\small \displaystyle \sum_{k=10}^{n}(k^2+3)\)
(3)\(\small \displaystyle \sum_{k=0}^{n+1} (k+n-a)\)
和の範囲が1~nではない場合の計算のポイントは、和の下限が1になるように式変形することです。
#和の上限が異なる場合
・\(\small \displaystyle \sum_{k=1}^{\color{#ff0055}{n+1}}f(k)\)の和みたいなパターン。
→ Σ公式の\(\small n\)を上限の値に置き換えよ!
#和の下限が1より大きな値の場合
・\(\small \displaystyle \sum_{k=\color{#ff0055}a}^{n}f(k)\)の和みたいなパターン。
→ \(\small a≦k≦n\)(\(\small 1<a<n\))の和であれば、
$$\small \sum_{k=a}^n f(k)=\color{#ff0055}{\sum_{k=1}^n} f(k)-\color{#ff0055}{\sum_{k=1}^{a-1}}f(k)$$
で求めよ!
【補足】数式だと分かりにくいかもしれないですが、『\(\small 1~n\)までの和(下図②)』から『\(\small 1~a-1\)までの和(③)』を引き算すれば、『\(\small a~n\)までの和(①)』が求まるということです。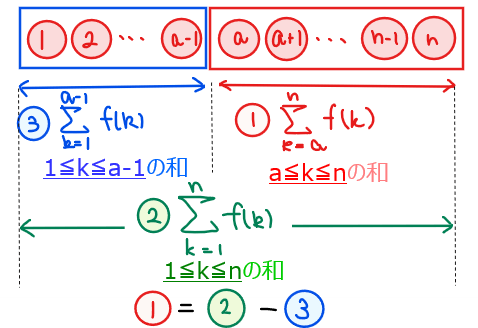
【注】\(\small a~n\)の和を求めたいので、引き算する和は\(\small 1~\color{#ff0055}{a-1}\)(\(\small 1~a\)ではない!)となる点に注意しよう。
#和の下限が0の場合
・\(\small \displaystyle \sum_{k=\color{#ff0055}0}^{n}f(k)\)の和みたいなパターン。
→ \(\small k=0\)の項と\(\small \displaystyle \color{#ff0055}{\sum_{k=1}^n} f(k)\)の和に分解。
【補足】Σ(シグマ)計算の注意点
・Σの和で使用される変数(\(\small \displaystyle \sum_k\)であれば\(\small k\)のこと)は文字自体には特に意味がない変数なので、\(\small k\)以外の文字が使われることもあります。計算自体は同じなので文字が変わることもあるという点を認識しておきましょう。…【問題(1)】
・シグマの和で使用される変数以外の文字は問題で特別な指定がない限りは定数(ただの数と同じ)になります。なので、間違って和の公式を適用しないように注意しましょう。…【問題(3)】
和の下限が1、上限が\(\small n-2\)なので、和の上限が異なるパターンであることから、Σの公式
$$\small \sum_{k=1}^n k^3 = \left\{\frac{1}{2}n(n+1)\right\}^2$$
で\(\small n\)を\(\small n-2\)に置き換えて
$$\small \sum_{k=1}^{\color{#ff0055}{n-2}} k^3 = \left\{\frac{1}{2}\color{#ff0055}{(n-2)}(\color{#ff0055}{(n-2)}+1)\right\}^2$$
とすればOKです。
また、冒頭の【補足】Σ(シグマ)計算の注意点でも記載した通り、Σの和の変数はどんな文字を使ってもよいので、\(\small k\)でも\(\small i\)でも同じなことに注意しましょう。
よって、
\begin{split}
\small \sum_{i=1}^{\color{#ff0055}{n-2}} i^3 &\small = \left\{\frac{1}{2}\color{#ff0055}{(n-2)}(\color{#ff0055}{(n-2)}+1)\right\}^2\\
&\small = \left\{\frac{1}{2}(n-2)(n-1)\right\}^2\\
&\small = \color{red}{\frac{1}{4}(n-2)^2(n-1)^2\space \cdots 【答】}\\
\end{split}
和の範囲が\(\small 10≦k≦n\)なので、下限が1より大きな値になっているパターンです。
よって、\(\small 1≦k≦n\)の和から\(\small 1≦k≦9\)の和を引き算します。
つまり
\begin{split}
&\small \sum_{k=10}^n (k^2+3) \\
\small =&\small \sum_{k=1}^n(k^2+3)-\sum_{k=1}^9 (k^2+3)\\
\end{split}
このようにΣの下限を1からの和に式変形して公式が使えるようにすることがポイントです。
あとはΣ公式を用いて計算するだけです。
●Σ公式を思い出そう
\begin{split}
&\small \sum_{k=1}^n k^2 =\frac{1}{6}n(n+1)(2n+1)\\
&\small \sum_{k=1}^n c =nc
\end{split}
\begin{split}
&\small \sum_{k=1}^n(k^2+3)-\sum_{k=1}^9 (k^2+3)\\
\small =&\small \left( \frac{1}{6}n(n+1)(2n+1)+3n \right) \space \color{#ef5350}{◀Σ公式を利用}\\
&\small -\left(\frac{1}{6}\cdot 9 \cdot 10 \cdot 19 + 3\cdot 9\right) \space \color{#ef5350}{◀n=9としてΣ公式を利用}\\
\small =&\small \frac{1}{6}n(n+1)(2n+1)+3n -312\\
\end{split}
最後に上式を一つの分数にまとめていきます。
上式を分母を通分すると
\begin{split}
&\small \frac{1}{6}n(n+1)(2n+1)+3n -312\\
\small =&\small \frac{n(n+1)(2n+1)+3n\cdot 6 -312\cdot 6}{6} \space \color{#ef5350}{◀分子は共通因数ないので展開して終わり}\\
\small =&\small \frac{2n^3+3n^2+n+18n -1872}{6}\\
\small =&\small \color{red}{\frac{1}{6}(2n^3+3n^2+19n -1872) \space \cdots 【答】}\\
\end{split}
和の範囲が\(\small 0≦k≦n+1\)なので、『和の上限が異なる』かつ『和の下限が0』のパターンになります。まずは和の下限を1に変形するために、\(\small k=0\)の項と\(\small 1≦k≦n+1\)の項に分けます。
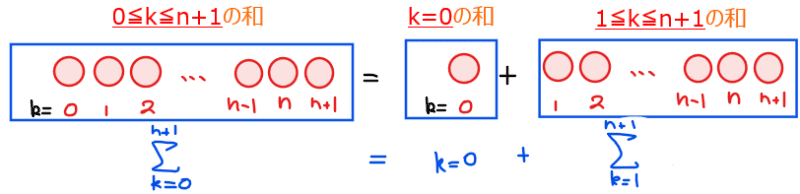
【補足】
このことを数式を使ってちょっと小難しく(数学的にしっかりと)書くと
\begin{split}
&\small \sum_{\color{#ff0055}{k=0}}^{n+1}f(k)= \color{#ff0055}{f(0)} + \sum_{\color{#ff0055}{k=1}}^{n+1}f(k)
\end{split}
となります。\(\small f(k)\)とは\(\small k\)を含んだ式のことで、今回であれば、\(\small f(k)=k+n-a\)になります。
\(\small k=0\)の項(\(\small f(0)\)の値)は、和をとる値 \(\small k+n-a\)に\(\small k=0\)を代入してあげればよいので、\(\small n-a\)…①となります。\(\small 1≦k≦n+1\)の和はΣを使って
\begin{split}
\small \color{#ff0055}{\sum_{k=1}^{n+1}}(k+n-a) \space \cdots ②
\end{split}
とそのまま表しておきます。
一旦、ここまでの内容を数式を使って整理しておきましょう。①、②より求める和は
\begin{split}
\small \sum_{k=0}^{n+1} (k+n-a) &\small = (k=0の項)+(1≦k≦n+1の和)\\
&\small = n-a + \sum_{k=1}^{n+1}(k+n-a) \space \cdots (*)
\end{split}
となります。あとは、\(\small \displaystyle \sum_{k=1}^{n+1}(k+n-a)\)の和が計算できればOKですが、これは『和の上限が異なる』パターンなので、Σ公式の\(\small n\)を\(\small n+1\)に置き換えすれば求められます。
よって、
\begin{split}
\small \sum_{k=1}^{n+1}(k+n-a) &\small =\sum_{k=1}^{n+1}k + \sum_{k=1}^{n+1}(n-a) \space \color{#ef5350}{◀分配法則}\\
&\small =\frac{1}{2}(\color{#ff0055}{n+1})((\color{#ff0055}{n+1})+1)\\
&\small \quad +(n-a)( \color{#ff0055}{n+1}) \space \color{#ef5350}{◀Σ公式} \space [*1]\\
&\small =\frac{1}{2}(n+1)(n+2)+(n-a)(n+1) \space [*2]\\
\end{split}
*1:【補足】Σ公式の計算について
\(\small \displaystyle \sum_{k=1}^{n+1}k\)に関しては、
$$\small \sum_{k=1}^n k =\frac{1}{2}n(n+1)$$
の公式で\(\small n\)を\(\small n+1\)に置き換えるだけです。
\(\small \displaystyle \sum_{k=1}^{n+1} (n-a)\)の計算については、\(\small n-a\)は変数\(\small k\)を含まない和なので、Σ公式
$$\small \sum_{k=1}^n c =nc$$
を使ってあげましょう。今回であれば\(\small c=n-a\)(定数)になります。
そのうえで、和の上限が\(\small n+1\)なので、
$$\small \sum_{k=1}^{\color{#ff0055}{n+1}} c =\color{#ff0055}{(n+1)}c$$
と考えて、\(\small c=n-a\)を代入してあげればよいでしょう。
*2:【補足】分数計算について
この式を通分して共通因数で括ってと式変形したくなりますが、このあと\(\small (*)\)の式に代入して1つの分数の形にまとめることを考えるとこの段階ではまとめずに、代入後の最終的な式の方でまとめる方が計算の手間が省けます。
この結果を求める和の式\(\small (*)\)に代入すると
\begin{split}
&\small n-a + \sum_{k=1}^{n+1}(k+n-a)\\
\small = &\small n-a +\frac{1}{2}(n+1)(n+2)+(n-a)(n+1)\\
\small = &\small \frac{1}{2}(n+1)(n+2)+(n-a)\color{#ff0055}{(n+2)} \space [*3]\\
\small = &\small \frac{(n+1)(n+2)+2(n-a)(n+2)}{2}\\
\small = &\small \frac{(n+2)\{(n+1)+2(n-a)\}}{2}\\
\small = &\small \frac{(n+2)(n+1+2n-2a)}{2}\\
\small = &\small \color{red}{\frac{1}{2}(n+2)(3n-2a+1) \space \cdots 【答】}\\
\end{split}
*3:【補足】
第1項目と第3項目に着目すると、\(\small n-a\)が共通因数になっているので
\begin{split}
&\small n-a +(n-a)(n+1) \\
&\small= (n-a)\{1+(n+1)\}\\
&\small= (n-a)(n+2)\\
\end{split}
と変形できます。
【応用問題】和の中抜け(差の形)を利用したΣ(シグマ)の和
次の和を求めよ。
(1)\(\small \displaystyle \sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)\)
(2)\(\small \displaystyle \sum_{k=1}^{n} k(k+1)(k+2)(k+3)\)
(1)\(\small \displaystyle f(k)=\frac{1}{k}\)とおくと、
\begin{split}
\small \sum_{k=1}^n\left(\frac{1}{k}-\frac{1}{k+1}\right)= \sum_{k=1}^n (f(k)-f(k+1))
\end{split}
のように\(\small f(k)\)と\(\small f(k+1)\)の差の形になっているため、『中抜けの和』を利用することで
\begin{split}
\small \color{#ff0055}{\sum_{k=1}^n (f(k)-f(k+1))=f(1)-f(n+1)}\\
\end{split}
のように、簡単に計算することができます。
(2)連続した積の和はうまく式変形すると\(\small f(k)\)と\(\small f(k+1)\)の差の形にできるので中抜けの和を利用して計算ができます。
Σの和をとる式を\(\small f(k)\)( = 変数\(\small k\)を含む式)とします。
Σの和をとる式が
$$\small \sum_{k=1}^n (f(k)-f(k+1))$$
のように変数\(\small k\)がズレている式の差の形になっている場合、この和は
$$\small \sum_{k=1}^n (\color{#ff0055}{f(k)-f(k+1)})=\color{#ff0055}{f(1)-f(n+1)}$$
となります。
これは、実際にΣの和を書き下すと
のように中身の和が打ち消し合うことから、最初と最後の項だけが残ります。
このことから、変数\(\small k\)の差を考えて和を求める手法は『中抜けの和』と呼ばれます。
\(\small \displaystyle f(k) = \frac{1}{k}\)と見なすと、\(\small \displaystyle \frac{1}{k+1}=f(k+1)\)なので、和の中身の式は\(\small f(k)-f(k+1)\)の差の形になっているので、中抜けの和の考え方が使えそうです。
よって、具体的にシグマの和を書き下していくことで
\begin{split}
&\small \sum_{k=1}^n \left(\frac{1}{k}-\frac{1}{k+1}\right)\\
\small = &\small \left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\cdots\\
&\small + \left(\frac{1}{n-1}-\frac{1}{n}\right)+\left(\frac{1}{n}-\frac{1}{n+1}\right)\\
\small = &\small 1-\frac{1}{n+1}\\
\small = &\small \color{red}{\frac{n}{n+1}\space \cdots 【答】}\\
\end{split}
【補足】
『中抜けの和』は公式を覚えて使うというよりは、Σの和の中身が、変数\(\small k\)がズレた式の差の形になっていたら、「中身が消えるパターンだな」と判断してシグマの和を書き下して解くのが良いと思います。
シグマの中身を頑張って展開してゴリ押す解法だと、\(\small k^4\)の項がでてきてしまうため、\(\small \displaystyle \sum_{k=1}^n k^4\)の部分が計算できずに行き詰ってしまします。
本問のように連続した積の和になっている問題では、和をとる式である\(\small k(k+1)(k+2)(k+3)\)を\(\small f(k)-f(k+1)\)の差の形に式変形して、中抜けの和を利用する解法が定石です。
では、\(\small k(k+1)(k+2)(k+3)\)を差の形で表せるような\(\small f(k)\)はどんな式になるのでしょうか?これは、ある程度、答の式を知っている必要があるので、結論から言うと
$$\small f(k) = (k-1)k(k+1)(k+2)(k+3) \space \cdots ①$$
とおいてあげます。和をとる式に\(\small k-1\)の積をくっつけるだけと覚えておけばよいでしょう。
このようにしておくと、\(\small f(k)-f(k+1)\)は
\begin{split}
&\small \small f(k)-f(k+1) \\
&\small = (k-1)k(k+1)(k+2)(k+3)\\
&\small \quad -k(k+1)(k+2)(k+3)(k+4) \space \color{#ef5350}{◀f(k+1)はkをk+1に置き換えるだけ}\\
&\small = k(k+1)(k+2)(k+3)\{(k-1)-(k+4)\}\space \color{#ef5350}{◀共通因数で括る}\\
&\small = -5k(k+1)(k+2)(k+3)\\
\end{split}
よって、
\begin{split}
&\small \small f(k)-f(k+1) = -5k(k+1)(k+2)(k+3)\\
\small ∴ \space &\small \small k(k+1)(k+2)(k+3)= -\frac{1}{5}\{f(k)-f(k+1)\} \space \cdots ②\\
\end{split}
これで、\(\small k(k+1)(k+2)(k+3)\)を\(\small f(k)\)と\(\small f(k+1)\)の差の形で表すことができました!
【研究】なぜ\(\small k-1\)を掛け算することでうまく求まるのか
\(\small f(k)-f(k+1) \)の式変形を見ると、\(\small k-1\)を掛け算したことによって、求めたい和の式である\(\small k(k+1)(k+2)(k+3)\)が共通因数として出てくることがポイントです。このポイントを押さえておけば、仮にかけ算する式を忘れてしまった場合でも求めたい和の式が共通因数として出てくるためには何を掛け算しておけばよいかという思考で見つけ出すことができると思います。
また補足として、問題によっては\(\small f(k)-f(k-1)\)の差の形を考える場合もあります(どちらでも求め方は同じ)。その場合は\(\small k+4\)を掛け算した式を\(\small f(k)\)と置けば共通因数に求めたい和の式が出てくることが分かります。
あとは、②の両辺にΣの和をとることで
\begin{split}
&\small \sum_{k=1}^n k(k+1)(k+2)(k+3)= -\frac{1}{5}\sum_{k=1}^n \{f(k)-f(k+1)\}\\
\end{split}
となるので、右辺は中抜けの和の考え方を利用することで
\begin{split}
&\small -\frac{1}{5}\sum_{k=1}^n \{f(k)-f(k+1)\}\\
\small = &\small -\frac{1}{5}\big[\{f(1)-f(2)\}+\{f(2)-f(3)\}+\cdots \\
&\small \quad +\{f(n-1)-f(n)\}+\{f(n)-f(n+1)\}\big]\\
\small = &\small -\frac{1}{5}\big[ f(1)-f(n+1)\big]\\
\small = &\small -\frac{1}{5}\big[ 0-n(n+1)(n+2)(n+3)(n+4)\big] \space \color{#ef5350}{◀①を利用} \space [*1]\\
\small = &\small \frac{1}{5}n(n+1)(n+2)(n+3)(n+4)\\
\end{split}
*1:【補足】\(\small f(1),f(n+1)\)の計算
①で、\(\small f(k)=(k-1)k(k+1)(k+2)(k+3)\)としていたので、\(\small f(1)\)であれば\(\small k=1\)、\(\small f(n+1)\)であれば\(\small k=n+1\)を代入することで計算ができます。
よって、
\begin{split}
&\small \sum_{k=1}^n k(k+1)(k+2)(k+3)\\
\small = &\small \color{red}{\frac{1}{5}n(n+1)(n+2)(n+3)(n+4) \space \cdots 【答】}\\
\end{split}
本記事のまとめ
本記事では、数列におけるΣ(シグマ)の和の求め方について、基本から応用まで解説しました。
Σの意味や基本的な計算方法に加え、シグマの公式を使ったあとの分数を含む式のくくり方や、k=1~n ではない場合の計算方法のコツ、さらには応用問題として頻出の和の中抜けの考え方を典型問題を通して整理しました。
Σの計算は公式を覚えるだけではなく、シグマで表された和が具体的にどのような和になっているのかをしっかりとイメージできることが重要です。
今回紹介した考え方を身につければ、複雑に見えるΣの式でも落ち着いて処理できるようになります。
数列が苦手な方や、定期テスト・入試で確実に得点したい方は、今回紹介した問題を繰り返し解きながら理解を深めてみてください。
今回は以上です。お疲れさまでした!







コメント