こんにちは、管理のhiroemonです。
本記事では、ガウス記号を含んだ数列の和の問題を解説していこうと思います。少し応用的な問題なので、「群数列ってそもそも何だっけ？」と思った方は、まず初めに「群数列の基本」の記事を読んでから問題に挑戦していただくのがよいかなと思います！
- 群数列の問題が解きたい！
- 応用的な数列の和の問題を解きたい！
- 群数列の和の計算のコツが知りたい！
このとき、 $$\sum_{n=1}^{100} \left[ \frac{n}{[\sqrt{n}]} \right]$$ を求めよ。
 |
新品価格 |
 |
新課程入試対応 数学難問集 100 (チャート式・シリーズ) 新品価格 |
1.【準備編】予備知識の復習
問題に行く前に、今回の問題を解く上で知っておかなければならない予備知識をいくつか紹介します。数列計算に自信がある人は飛ばしてokで、問題編にいきましょう。
1.1 数列の和の公式
これは一応載せておきます。しっかり覚えちゃいましょう！
$$ \begin{equation} \begin{split} & \sum_{k=1}^n 1 = n\\ &\sum_{k=1}^n k = \frac{1}{2}n(n+1)\\ &\sum_{k=1}^n k^2 = \frac{1}{6}n(n+1)(2n+1) \end{split} \end{equation} $$
1.2 ガウス記号
ガウス記号とは、[3]=3、[3.1]=3、[3.6]=3、[3.9999]=3、[4.01]=4のように、ブランケットの中身の整数部分を表す記号です。いくつか練習していましょう。
(1)\(\small \left[ \frac{5}{2} \right]\)
(2)\(\small \left[ \sqrt{35} \right]\)
(3)\(\small \left[ \pi \right]\)
(4)\(\small \left[ \log_{2}25 \right]\)
→\(\small \frac{5}{2}= 2.5\)なので。
（2）5
→\(\small 5 (=\sqrt{25}) < \sqrt{35} < 6(=\sqrt{36}) \)なので。
（3）3
→3.14\(\small \cdots \)なので。
（4）4
→\(\small 4(=\log_2 16) < \log_2 25 < 5(=\log_2 32) \)なので。
2.【問題編】ガウス記号を含む数列の和
このとき、 $$\sum_{n=1}^{100} \left[ \frac{n}{[\sqrt{n}]} \right]$$ を求めよ。
この問題の1文目は、難しそうな説明が書かれていますが、予備知識でお伝えしたガウス記号の定義が書かれているだけですね。
では本題の数列の和の計算ですが、このままでは、「1.1数列の和の公式」で紹介したような公式が使える形になっていないので、まずは公式が使える形になるように規則性を見つけ出す必要があります。
2.1 規則性の予想
最初の数項を試しに計算してみましょう。
■第1項目（n=1）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=1}=\left[ \frac{1}{[\sqrt{1}]} \right]=1$$
■第2項目（n=2）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=2}=\left[ \frac{2}{[\sqrt{2}]} \right]=\left[ \frac{2}{1} \right]=2$$
途中式の変形はガウス記号の定義に従って、\(\small [\sqrt{2}]=1\)になります。
■第3項目（n=3）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=3}=\left[ \frac{3}{[\sqrt{3}]} \right]=\left[ \frac{3}{1} \right]=3$$
■第4項目（n=4）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=4}=\left[ \frac{4}{[\sqrt{4}]} \right]=\left[ \frac{4}{[2]} \right]=\left[ \frac{4}{2} \right]=2$$
■第5項目（n=5）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=5}=\left[ \frac{5}{[\sqrt{5}]} \right]=\left[ \frac{5}{2} \right]=2$$
■第6項目（n=6）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=6}=\left[ \frac{6}{[\sqrt{6}]} \right]=\left[ \frac{6}{2} \right]=3$$
■第7項目（n=7）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=7}=\left[ \frac{7}{[\sqrt{7}]} \right]=\left[ \frac{7}{2} \right]=3$$
■第8項目（n=8）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=8}=\left[ \frac{8}{[\sqrt{8}]} \right]=\left[ \frac{8}{2} \right]=4$$
■第9項目（n=9）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=9}=\left[ \frac{9}{[\sqrt{9}]} \right]=\left[ \frac{9}{3} \right]=3$$
■第10項目（n=10）
$$\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=10}=\left[ \frac{10}{[\sqrt{10}]} \right]=\left[ \frac{10}{3} \right]=3$$
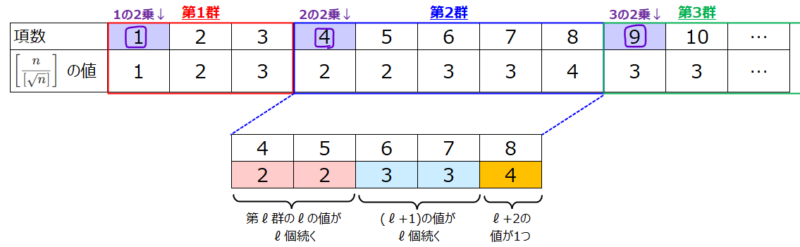
このくらいで一旦ストップしておきましょう。結果をまとめると下図の通り。
一見何の規則性もなさそうですが、よく見ると、値が小さくなるタイミングでグループに分けることができそうです（図1参照）。
ここで、それぞれのグループを第\(\small \ell\)群(\(\small \ell=1,2,3,\cdots\))として、群数列とみなして考えることにします。すると、いくつかの規則性に気づけるかなと思います。
■規則性の予想
第\(\small \ell\)群の先頭を第\(\small \ell^2\)項目と定義した場合、
- 第\(\small \ell\)群の項数は\(\small 2\ell+1\)
→第一群は3項、第2群は5項、第3群は7項（計算するとわかる）となっている。 - 第\(\small \ell\)群の値の構成は、先頭から\(\small \ell\)が\(\small \ell\)項、\(\small (\ell+1)\)が\(\small \ell\)項、\(\small (\ell+2)\)が1項
→例えば第2群だと「2」の値が2項,「3」の値が2項,「4」の値が1項となっている。
この予想が正しければ、各群ごとの和を計算して足し合わせていく計算は「数列の公式」を使って解くことができるので、これからそれぞれ証明していきましょう。
2.2 予想の証明
予想1：第\(\small \ell\)群の項数は\(\small 2\ell+1\)
これは群の定義から、第\(\small \ell\)群の初項が\(\small \ell^2\)項目、第\(\small (\ell+1)\)群の初項が\(\small (\ell+1)^2\)項目であることから、第\(\small \ell\)群の末項が\(\small (\ell+1)^2-1\)項目ということになるので、
$$((\ell+1)^2-1)-\ell^2+1=\ell^2+2\ell+1-1-\ell^2+1=2\ell+1$$
予想2：第\(\small \ell\)群の値の構成
第\(\small \ell\)群の項数が\(\small 2\ell+1\)項あることが分かったので次はその値の構成が、先頭から\(\small \ell\)が\(\small \ell\)項、\(\small (\ell+1)\)が\(\small \ell\)項、\(\small (\ell+2)\)が1項を証明する。
群の先頭（第\(\small \ell^2\)項目）から値が\(\small \ell\)の項が\(\small \ell\)個続くとすると、\(\ell^2+\ell-1\)項目までは値が\(\small \ell\)になるはずなので、まずはこれを証明する。
\(\small \ell^2 \leq n \leq \ell^2+\ell -1\)の場合、\(\small n=\ell^2+r\)、ただし、\(\small 0 \leq r \leq \ell -1\)とおくことができる。このときの値は、
$$
\begin{equation}
\begin{split}
\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=\ell^2+r}&=\left[ \frac{\ell^2+r}{[\sqrt{\ell^2+r}]} \right]=\left[ \frac{\ell^2+r}{\left[\sqrt{\ell^2 \left( 1+\frac{r}{\ell^2}\right)}\right]} \right]=\left[ \frac{\ell^2+r}{\ell \left[\sqrt{\left( 1+\frac{r}{\ell^2}\right)}\right]} \right] \cdots (*)
\end{split}
\end{equation}
$$
ここで、
$$
\begin{equation}
\begin{split}
&\left[\sqrt{\left( 1+\frac{r}{\ell^2}\right)}\right]\\
\end{split}
\end{equation}
$$
は、\(\small 0 \leq r \leq \ell -1\)であることから、
$$0 \leq \frac{r}{\ell^2} \leq \frac{\ell -1}{\ell^2}$$
$$1 \leq 1+ \frac{r}{\ell^2} \leq 1+\frac{\ell -1}{\ell^2}$$
$$1 \leq 1+\frac{r}{\ell^2} \leq 1+\frac{1}{\ell}-\frac{1}{\ell^2} < 2$$
1以上、2未満の値なので、ガウス記号にかけると1となる。
$$\left[ \frac{\ell^2+r}{\ell \left[\sqrt{\left( 1+\frac{r}{\ell^2}\right)}\right]} \right]
=\left[ \frac{\ell^2+r}{\ell} \right]=\left[ \ell+\frac{r}{\ell} \right]$$
このガウス記号も、
$$\ell \leq \ell+\frac{r}{\ell} \leq \ell+\frac{\ell-1}{\ell}$$
$$\ell \leq \ell+\frac{r}{\ell} \leq \ell+1-\frac{1}{\ell} < \ell + 1$$
つまり、
$$\ell \leq \ell+\frac{r}{\ell} < \ell + 1$$
となるので、問題文1文目にもある定義から、ガウス記号をとると\(\small \ell\)になることを利用することで、
$$
\begin{equation}
\begin{split}
\left[ \ell+\frac{r}{\ell} \right]=\ell
\end{split}
\end{equation}
$$
であることが分かる。
次に\(\small (\ell^2+\ell)\)項目から\(\small (\ell +1)\)が\(\small \ell\)項続くことを証明する。
すなわち、\(\small \ell^2+\ell \leq n \leq\ell^2+2\ell -1 \)のときの\(\small \left[ \frac{n}{[\sqrt{n}]} \right]\)の値が\(\small \ell+1\)であることを証明する。
\(\small n=\ell^2+r\)（\(\small \ell \leq r \leq 2\ell -1 \)）とおくと、\(\small (*)\)の式中にある
$$
\begin{equation}
\begin{split}
&\left[\sqrt{\left( 1+\frac{r}{\ell^2}\right)}\right]\\
\end{split}
\end{equation}
$$
は、
$$\ell \leq r \leq 2\ell -1$$
$$\frac{1}{\ell} \leq \frac{r}{\ell^2} \leq \frac{2\ell -1}{\ell^2}$$
$$1+\frac{1}{\ell} \leq 1+\frac{r}{\ell^2} \leq 1+\frac{2}{\ell}-\frac{1}{\ell^2}$$
よって、1と2の間の値なので
$$\left[\sqrt{\left( 1+\frac{r}{\ell^2}\right)}\right]=1$$
となるので
$$\left[ \frac{\ell^2+r}{\ell \left[\sqrt{\left( 1+\frac{r}{\ell^2}\right)}\right]} \right]
=\left[ \frac{\ell^2+r}{\ell} \right]=\left[ \ell+\frac{r}{\ell} \right]$$
このガウス記号の計算も
$$\ell \leq r \leq 2\ell -1$$
$$1 \leq \frac{r}{\ell} \leq \frac{2\ell -1}{\ell}$$
$$\ell +1 \leq \ell +\frac{r}{\ell} \leq \ell +2-\frac{1}{\ell}$$
$$\ell +1 \leq \ell +\frac{r}{\ell} < \ell +2$$
であることから、
$$\left[ \ell+\frac{r}{\ell} \right]=\ell +1$$
となる。
最後に、\(\small \ell +2\)が1項あることを証明する。
第\(\small \ell\)群の最後の項は、\(\small n=\ell^2+2\ell\)なので
$$
\begin{equation}
\begin{split}
\left[ \frac{n}{[\sqrt{n}]} \right] \Biggm\vert_{n=\ell^2+2\ell}&=\left[ \frac{\ell^2+2\ell}{[\sqrt{\ell^2+2\ell}]} \right]=\left[ \frac{\ell^2+2\ell}{\left[ \sqrt{\ell^2(1+\frac{2}{\ell})}\right]} \right]\\
&=\left[ \frac{\ell^2+2\ell}{\left[\ell \sqrt{(1+\frac{2}{\ell})}\right]} \right]=\left[ \frac{\ell^2+2\ell}{\ell} \right]\\
&=\left[\ell+2 \right]=\ell+2
\end{split}
\end{equation}
$$
以上から、予想が正しいことを証明できた。
2.3 数列計算
今回求める数式は第100項目までの和なので、今回の和に含まれる群は、第1群～第9群+100項目になります。
第\(\small \ell\)群の和は、群の規則性から
$$
\begin{equation}
\begin{split}
(第\ell群の和)&=(\ell)\times\ell+(\ell+1)\times\ell+(\ell+2)\times1=\ell^2+(\ell^2+\ell)+(\ell+2)\\
&=2(\ell^2+\ell+1)
\end{split}
\end{equation}
$$
よって、求める数列の和は、
$$
\begin{equation}
\begin{split}
\sum_{n=1}^{100} \left[ \frac{n}{[\sqrt{n}]} \right]&=\sum_{\ell=1}^9 \{2(\ell^2+\ell+1)\} +\left[ \frac{100}{[\sqrt{100}]} \right]\\
\end{split}
\end{equation}
$$
第1項目の和について、
$$
\begin{equation}
\begin{split}
\sum_{\ell=1}^9 \{2(\ell^2+\ell+1)\}&=2\sum_{\ell=1}^9 (\ell^2+\ell+1)\\
&=2\left( \frac{1}{6}\cdot 9\cdot10\cdot19+\frac{1}{2}\cdot9\cdot10+9\right)\\
&=2(285+45+9)\\
&=678
\end{split}
\end{equation}
$$
また、
$$\left[ \frac{100}{[\sqrt{100}]} \right]=10.$$
よって、求める数列の和は
$$678+10=688\quad \cdots (答)$$
3.まとめ
ガウス記号を含む数列計算の応用問題はいかがでしたか？少し計算が複雑でしたが、規則性が分かってしまえばあとは計算するだけの問題なので、いかに規則性を見抜くかがポイントになる問題でした。
規則性を見つけ出すポイントは、具体的に計算をしてみて数字を眺めてたり、計算する過程で何かの法則に気が付くということも多いので、この種の問題は粘り強く計算して規則性を見つけていきましょう。
では本日はここまでです。お疲れさまでした！
