本記事では、円の接線に関する問題の解き方を解説します。接線を求める問題は、解法をある程度パターン化して整理していないと計算でつまづいてしまうことが多いため、数学が得意な人でも「なんで自分の解法じゃうまく解けないんだろう…」といった疑問が生じやすい分野になっています。また、解き方自体もいろいろな方法がありますが、思い付きの解法では計算が複雑すぎて解けないことがほとんどです。そういった特徴もこの分野が苦手な人が多い理由かと思います。
- 解き方の方針が知りたい!
- 計算が複雑すぎて途中で行き詰ってしまうことが多く困っている…
- 接線の公式は分かるけど問題でどう使えばよいかわからない…
【知識編】円と接線の問題を解くコツ
■円と接線の問題を解くコツ
・【Point1】解き始める前に計算が簡単になる解法を考える
・【Point2】使う文字は2つまでを目安にする
・【Point3】計算に詰まったら方針を見直す
【Point1】計算が簡単になる解法を考える
円と接線の問題を解く上で最も重要なのが、計算し始める前に計算が楽になるような解法を見つけることです。
こういうと、「計算する前から解法を見通すなんてできないよ…」、「自分は計算が複雑でも頑張って解くから大丈夫」といった人も出てくるかもしれませんが、ここが一番肝心といっても過言ではありません。この工程を飛ばすというのは、いわばレシピを見ずに初めての料理を作るようなものです。これでは、どんな高級食材がそろっていてもおいしい料理は作れません。
では、なぜ計算が複雑にならない解法を考えることがそこまで大事かというと、円と接線の問題には「方程式が複雑な計算になりやすい」、「文字数が多くなりやすい」という特徴があるからです。
方程式が複雑になりやすい
円の方程式は一般に\(\small (x-a)^2+(y-b)^2=r^2\)といった2次式になります。接線の方程式は、\(\small (x_1-a)(x-a)+(y_1-b)(y-b)=r^2\)のようなは1次式ですが、1つの接線を求めるためには、接点を\(\small (x_1,y_1)\)のように2つの文字を使わなければいけません。そして、接線の方程式や接点を求めるためには、これらを連立する必要があるので、2つの文字を含んだ2次方程式を解かないといけません。計算も分数計算になることが多いです。
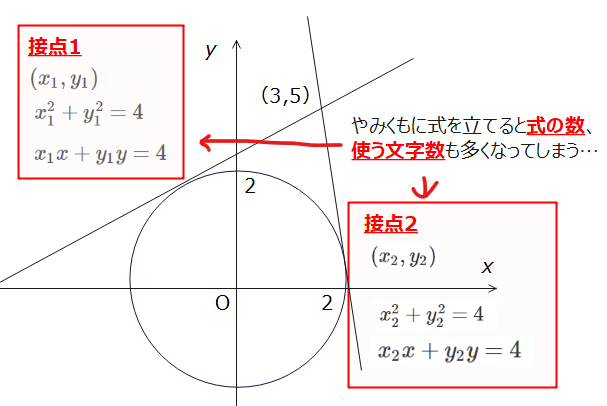
そのため、やみくもに解いても計算に行き詰まったり、計算ミスが起こってしまうのです。
文字数が多くなりやすい
接線を求めるには、接点を\(\small (x_1,y_1)\)のように置く必要があり、これだけで2つの文字を使います。他にも、円の方程式として\(\small x^2+y^2+\ell x +my+n=0\)を使う場合は、3つも文字が出てきます。もし半径が分かっているなら、\(\small (x-a)^2+(y-b)^2=4\)のように文字を2つに減らせます。どちらの式でも解くことができますが、どれを使うかで解きやすさが全然異なるので、なるべく文字数が少なくなる公式を選びましょう。
これらの2つ罠にまんまとはまらないためにも、計算が複雑にならないような解き方の見極めをするようにしましょう。
【Point2】使う文字は2つまでを目安にする
「計算が複雑にならないような解法を考えるといっても具体的にどう考えればいいの?」という疑問を持った人も多いかと思います。なので、具体的には「使う文字は2つまで」を目安にするとよいでしょう。
もし3つや4つも文字を使って解く方法しか思いつかないときは、他にシンプルな方法があることが多いです。たとえば、図形的な性質を利用して解くことができないか考えてみましょう。
【Point3】計算に詰まったら方針を見直す
はじめに計算の手間がかからなさそうな解法を思いついて計算を進めていったときに、途中でやっぱり計算が複雑になってしまった、ということはよく起こります。そういう場合は、無理に計算を進めるのではなく、他にシンプルな解法がないか再度確認しましょう。
最後に、これまで複雑な計算は避けましょうとお伝えしましたが、中には複雑な計算が必要な問題もあります。なので、検討した結果やっぱりこの解き方しかないのであれば、複雑だとしても解くしかないのでそこは誤解しないように注意が必要です。
【解説編】円と接線の問題の解き方
【問題1】接線の求め方(基本問題)
円\(\small x^2+y^2=r^2\)で接点\(\small (x_1,y_1)\)における接線の方程式は $$x_1x+y_1y=r^2$$
接点を\(\small (p,q)\)とおくと接線の方程式は公式より
$$px+qy=1 \quad \cdots①$$
この接線が点\(\small (2,1)\)を通ることから
$$2p+q=1 \quad \cdots②$$
を満たす。また、接点は円\(\small x^2+y^2=1\)上の点なので、
$$p^2+q^2=1\quad\cdots③$$
を満たす。②は\(\small q=-2p+1\)より③に代入することで
$$
\begin{equation}
\begin{split}
&p^2+(-2p+1)^2=1\\
&p^2+4p^2-4p+1=1\\
&5p^2-4p=0\\
&p(5p-4)=0\\
&p=0,\frac{4}{5}
\end{split}
\end{equation}
$$
よって、\(\small p=0\)のとき\(\small q=1\)、\(\small p=\frac{4}{5}\)のとき\(\small q=-\frac{3}{5}\)となるため、求める接線の方程式は、これらを①に代入することで
$$
\begin{equation}
\begin{split}
&y=1\quad\cdots(答)\\
&\frac{4}{5}x-\frac{3}{5}y=1\\
&4x-3y=5\quad\cdots(答)
\end{split}
\end{equation}
$$
【問題2】極線の方程式(標準問題)
円の外部の1点から引いた2つの接線の接点を通る直線を、その円の極線という。
そして極線の方程式は、外部の点を\(\small (p,q)\)、円\(\small x^2+y^2=r^2\)とすると、 $$px+qy=r^2$$
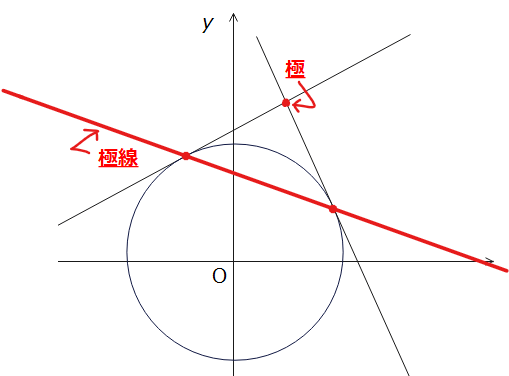
この問題は、まともに解こうとすると次のような手順で解く必要があります。
この手順で解いてももちろん答えは出てきますが、特にstep2で解く方程式は、式も文字も4つもありますし、2次方程式になることから計算がかなり複雑になります。
このように、計算を始める前に複雑な計算になることが見えた場合は、一旦方針を見直しましょう。より簡単な解き方がある場合がほとんどです。
今回だと、step2の上2つの式に着目します。
$$2x_1+y_1=1,\quad 2x_2+y_2=1$$
これは、2点\(\small (x_1,y_1),(x_2,y_2)\)がどちらも直線\(\small 2x+2y=1\)上にあることを表しています。
よって、答えは、\(\small 2x+y=1\quad\cdots(答)\)。
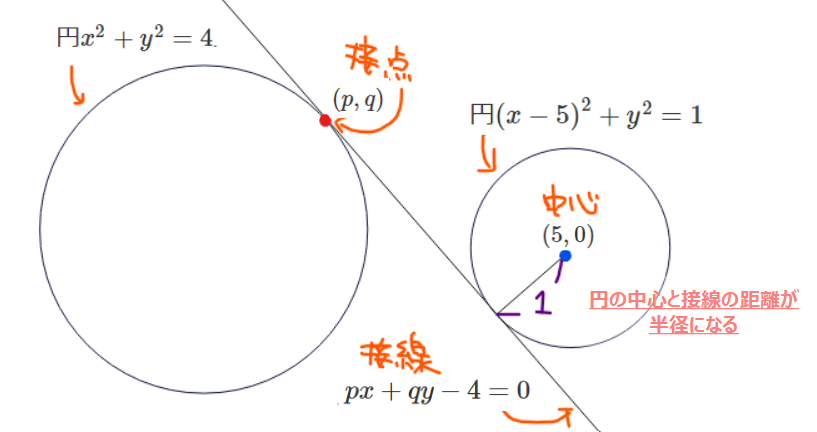
【問題3】2つの円の共通接線の求め方(応用問題)
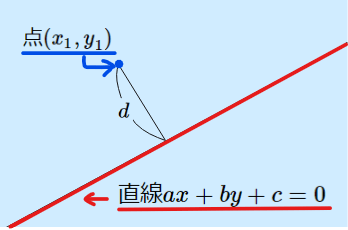
点と直線の距離の公式を使って解くべし!
点\(\small (x_1,y_1)\)と直線\(\small ax+by+c=0\)との距離\(\small d\)は, $$d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
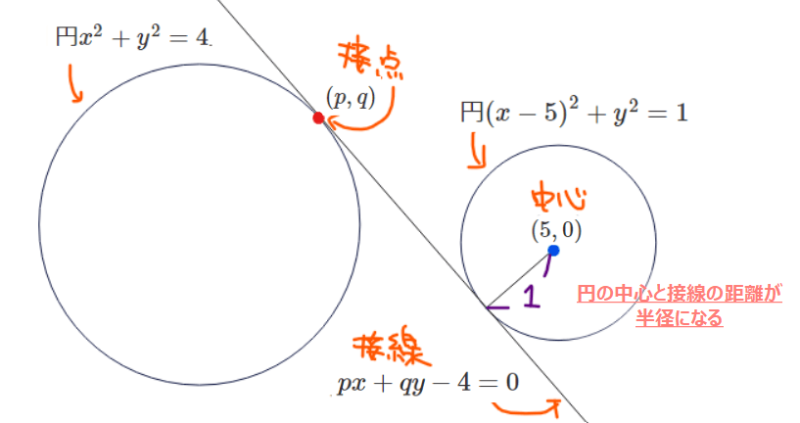
円\(\small x^2+y^2=4\)上の接点を\(\small (p,q)\)とおくと、接線の方程式は
$$px+qy=4\quad ⇔\quad px+qy-4=0\quad \cdots ①$$
また、接点\(\small (p,q)\)は円上の点なので、
$$p^2+q^2=4\quad \cdots ②$$
を満たす。
ここで接線①は円\(\small (x-5)^2+y^2=1\)の接線でもあることから、①の接線と円の中心\(\small (5,0)\)との距離は、円の半径1になる必要がある。
よって、点と直線の距離の公式より
$$
\begin{equation}
\begin{split}
&1=\frac{|5p-4|}{\sqrt{p^2+q^2}}\\
&1=\frac{|5p-4|}{\sqrt{4}}\\
&|5p-4|=2\\
\end{split}
\end{equation}
$$
ただし、2番目の式で②の関係式を用いた。
絶対値を外すために両辺を2乗して式を解くと
$$
\begin{equation}
\begin{split}
&(5p-4)^2=4\\
&25p^2-40p+16=4\\
&25p^2-40p+12=0\\
&(5p-2)(5p-6)=0\\
&p=\frac{2}{5},\frac{6}{5}
\end{split}
\end{equation}
$$
②より、\(\small p=\frac{2}{5}\)のときの\(\small q\)の値は、
$$\left( \frac{2}{5}\right)^2+q^2=4$$
$$\frac{4}{25}+q^2=4$$
$$q^2=\frac{96}{25}$$
$$q=\pm \frac{4\sqrt{6}}{5}\quad \cdots ③$$
同様に、\(\small p=\frac{6}{5}\)のときの\(\small q\)の値は、
$$q=\pm \frac{8}{5}\quad \cdots ④$$
③、④より共通接線の方程式は、次の4つ存在する。
[1]\(\small (p,q)=\left(\frac{2}{5},\pm \frac{4\sqrt{6}}{5}\right)\)のとき
求める接線の方程式は、①に代入することで
$$\frac{2}{5}x \pm \frac{4\sqrt{6}}{5}y-4=0$$
$$2x \pm 4\sqrt{6}y-20=0$$
$$x \pm 2\sqrt{6}y-10=0$$
[2]\(\small (p,q)=\left(\frac{6}{5},\pm \frac{8}{5}\right)\)のとき
同様にして、
$$3x \pm 4y-10=0$$
よって、共通接線の方程式は、
$$
\begin{equation}
\begin{split}
&x \pm 2\sqrt{6}y-10=0\\
&3x \pm 4y-10=0 \quad \cdots (答)
\end{split}
\end{equation}
$$
まとめ
今回は、円と接線の問題について解き方のコツと実際の問題での解き方を解説しました。
円と接線の方程式の問題は、数学が得意な人でもやみくもに計算を進めるとかなり計算が大変になりやすく、それがこの分野が苦手になる人が多い理由であることを解説しました。
そのために、計算がなるべく簡単になる解法を考えること、具体的には使う文字が2つ程度になるような解き方にすることをお伝えし、もし計算途中で思ったより計算が大変になってしまった場合は、そのまま計算をするのではなく別の解き方がないかを考えるというのが、この問題を解くときに大事な考え方になります。
他にもたくさんのパターンの問題がありますが、それぞれの解き方のコツは受験生であればある程度パターン化しておく必要があるので、そのあたりの問題も別途解説していきたいと思います。
それでは本日はここまでです。お疲れさまでした!


コメント