今回は、対数とは何かについて解説してきます。この記事を読むことで、「言葉は知っているけど、イマイチピンとこない…」、「対数計算の公式の意味を理解したい!」という悩みが解決できる内容になっています。また、最後には対数が日常生活でどのように使われているのかが分かる問題も用意しているので、ぜひ最後までチェックしてみてください!
1.対数の意味
1.1. 対数の起源
対数について詳しく説明する前に、そもそもなんで対数というものが生まれたのかを説明します。
昔、こんなことを考える数学者がいました。
市民:「ねぇ、2の3乗ってなに?」
数学者:「2の3乗は8だよ。2×2×2というように、2を3回掛け算すればいいんだよ。」
市民:「分かった!じゃあ、1024って2の何乗?」
数学者:「10乗だよ。2を10回、掛け算すると1024になるよ。」
市民:「おっけー。じゃあ、10って2の何乗?」
数学者:「え?…(聞こえないふり)」
もちろん、作り話ですが、10が2の何乗なのかについて、当時の数学では表すことができなかったためこれはまずい、ということで、数学的に、「〇を△乗した数」をすべて表せるようにしよう!という研究が盛んになりました。そこで、出てきたのが、「対数」というわけです。
数学者:「おい、市民。そういえばこの間聞かれた10が2の何乗か問題だけど、\(\small \log_2 10\) 乗だったよ。」
市民:「…」
1.2. 用語の意味
・対数とは、何乗するかを表す数字のこと。
・底とは、何乗するかの元になる数字のこと。
・真数とは、何乗かした結果の数字のこと。
ポイントでまとめた用語の意味について、解説していきます。
例えば、先程の例にでてきた、\(\small \log_2 10\) を日本語訳するのであれば、「2を何乗すると10になるかを表す数字」となります。底が2(何乗するかの元)、真数が10(何乗したかの結果)、対数が\(\small \log_2 10\) 自体になります。
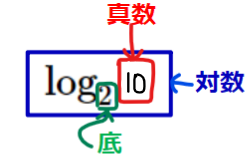
もう少し、違った説明をするのであれば、底、真数、対数の関係は、下の図のようになります。

底の対数乗が真数ということです。つまり、対数って指数のことなんです。
さらに別の説明をするのであれば、\(\small 2^x = 10\)の答えが、\(\small x=\log_2 10\)になります。なぜならば、そもそも\(\small \log_2 10\)とは、2を何乗したら、10になるかを表す数字だからです。
言葉遊びみたいになってしまいましたが、いろいろな角度から対数の意味を説明してみました。
自分の中で、しっくりくる説明の方法で覚えていおきましょう。
2を\(\small \log_2 10\)乗すると10になる、とはいえ、具体的に何乗なの?と思った人もいたかもしれません。
実際の計算は関数電卓を使用しないと出てきませんが、\(\small \log_2 10\)=3.3219…です。2を3.3219…乗すると、10になるということですね。
確かに、2の3乗が8、2の4乗が16なので、3と4の間にありそうと考えると、このくらいの数字になりそうです。
ポイントは、出てきた数字が規則性なく無限に続く小数になっているということ。このような数字を、数学では無理数といいます。
無理数は、小数や分数などで表すことができないので、logといったような新しい概念を使って表すしかなかったのです。
2. 対数の性質
対数の性質は、前章で説明した対数の成り立ちを考えると簡単です。
(性質1) \(\small \log_aAB = \log_aA+\log_aB\)
(性質2) \(\small \log_a\frac{A}{B} = \log_aA-\log_aB\)
(性質3) \(\small \log_aA^n = n\log_aA\)
logが出てくるとややこしいので、言葉に直して考えます。例えば、性質1から見てみましょう。\(\small\log_aA\)は「aを何乗かするとAになる」でした。何乗かするとだとわかりにくいので、「aをx乗したらAになる」としておきます。\(\small\log_aB\)も同様に、「aをy乗したらBになる」とします。\(\small\log_aAB\)が難しそうですが、同じ要領で、「aをz乗したらABになる」ですね。
日本語訳ができたので、今度は、数式に変換します。「aをx乗したらAになる」は、数式にすると、\(\small a^x=A\)となります。同じように残りも変換すると、\(\small a^y=B\)、\(\small a^z=AB\)ですね。ここで、ABはAとBの掛け算なので、すなわち、\(\small a^x\)と\(\small a^y\)の掛け算です。計算すると、\(\small AB=a^x×a^y=a^{x+y}\)ですね。ABはもともと、\(\small a^z\)だったので、指数部分を見比べると、\(\small x+y=z\)となるわけです。
これは、指数法則のことで、掛け算した場合、指数は、足し算になるという法則でした。これが、性質1とどんな関係があるのか?と思ったかもしれませんが、\(\small x+y=z\)自体がもう、性質1を表してます。xって何だったかと振り返ると、「aを何乗かするとAになる数字」でしたね。つまり、\(\small\log_aA\)のことです。同様にyは\(\small\log_aB\)、zは\(\small\log_aAB\)のことなので、代入してあげると、性質1の式になります。つまり、性質1は単に、掛け算すると、指数は足し算になるよ、ということを言っているだけですね。
性質2も1と同じで、今度は割り算すると指数は引き算になるよということです。これも、指数法則をしっかり理解できていれば、簡単ですね。割り算しているので、その分掛け算されている回数が減るよってことです(詳しくはこちら)。
性質3もやっぱり同じで、指数法則の、\(\small (a^x)^n=a^{nx}\)になる、つまり指数が掛け算になるということを言っているだけです。
こんな感じで、意味まで覚えておくと、忘れにくいと思います。
対数の性質を指数法則と比較してみます。まず、指数法則は以下の性質でした。
(性質1) \(\small a^x×a^y=a^{x+y}\)
(性質2) \(\small a^x÷a^y=a^{x-y}\)
(性質3) \(\small (a^x)^n=a^{nx}\)
次に、この性質と対数の性質を見比べてみます。
性質1同士を見ると、\(\small\log_aAB\)は、ABのように 2つの数字をかけた時の指数がどうなっているかを表しており、それは指数法則性質1から、それぞれの指数の 和になる(\(\small = \log_aA+\log_aB\))ことを表しています。
性質2は割り算の場合で、割り算の時は、指数の差になるんでした。理由は、例えば、具体例で考えると、\(\small 2^5÷2^3\)であれば、指数を使わずに書き下すと
$$\frac{2×2×2×2×2}{2×2×2}$$ のように、分子に2が5回掛け算されて、分母に2が3回掛け算されたものがきます。これを約分すると、分母の3つ分が 分子と打ち消し合うため、結果として、\(\small 2^2\)になります。つまり、割る数の指数分だけ、割られる数から引き算される というのが、性質2の指数法則であり、対数の性質2ということです。
指数法則の性質3について、これも具体例で考えると\(\small (2^2)^3\)であれば、書き下すと、\(\small (2^2)×(2^2)×(2^2)\)と\(\small 2^2\)が3回掛け算されるので合計として\(\small 2^6\)になるね、ということです。この時指数部分は、\(\small 2^2\)の3セット分ということで2×3=6と計算して求められる、ということを表しています。対数の性質3の\(\small n\log_aA\)という部分が、\(\small \log_aA\)(もともとの指数)をn倍すればいいということを表しているのです。
最後に、指数法則と対数の性質が対応していることは分かったけど、結局同じことを言っているのであれば、なんでわざわざ対数なんて使うの?指数でいいじゃん、と思った方がいるかもしれないので、補足します。結論としては、どちらも同じことなので、どっちを使っても大丈夫です。ですが、対数を使うことで、次のようなメリットがあります。
・指数の掛け算や割り算が、対数では足し算、引き算に置き換わるため計算が容易
・数値計算をする場合、指数を使うと桁あふれを起こしやすいが、対数であれば数値が大きくならずに計算可能
・指数部分が複雑な式の場合、指数表記だと、式が小さくなり見づらい
1つだけ具体例を挙げると、例えば、\(\small 2^{100}÷2^{98}\)を計算するときに、計算機で\(\small 2^{100}\)と\(\small 2^{98}\)を 計算して割り算すれば理論上は計算できますが、桁数が膨大になるため、桁あふれ(計算結果が、計算機上で使用できる桁数を超えてしまうこと。例えば、3桁までしか表示できない電卓の場合、1200を入力すると4桁目はあふれてしまい、200で表示される)を起こします。 そこで、計算時に対数の性質2と3を使用すると、\(\small log_2 (2^{100}÷2^{98})=log_2 2^{100}-log_2 2^{98}=100-98=2\)のように計算ができます。最後に、\(\small log_2 (2^{100}÷2^{98})=2\)であることから、答えは4と計算できるのです。 このようなメリットがあるため、対数は指数の計算をする際に有用です。
3.対数の実用例
では、対数について理解したところで、実際にどのように使われるのかを見てきます。
大腸菌(E. coli)は、人間の腸内に存在する菌で、汚染された水や食品を摂取することで感染し、人体に悪影響を及ぼすことが知られています。そんな大腸菌は、好条件下では、約20分で2分裂します。今、患者Aの体内に100個の大腸菌が検出されました。この場合、おおよそ何時間後に、感染症を引き起こすと考えられるでしょうか。ただし、条件は以下とします。
#体内の大腸菌が1万個を超えた時点で、感染症を発症するものとする。
#分裂速度は、好条件下として考える。
#\(\small \log_{10} 2=0.301\)とする。
感染時間を求めるには、大腸菌が1万個を超えるまでの分裂回数が分かればをよいです。そこで分裂回数を\(\small n\)回とします。20分で1回分裂して2倍になるので、大腸菌の個数は100×2=200個になります。開始から40分後には、2回分裂しているので100×\(\small 2^2\)=400個、1時間後には、3回分裂しているので、100×\(\small 2^3\)=800個になります。よって、n回分裂した場合は、\(\small 100×2^n\)となるので、これが1万を超えるという式を立てると $$100×2^n ≧ 10000$$ です。整理すると $$2^n ≧ 100$$ この式の両辺の対数をとると、 $$\log_{10} 2^n ≧ \log_{10} 100$$ 対数の性質3を使うと、 $$\log_{10} 2^n ≧ \log_{10} 10^2$$ $$n\log_{10} 2 ≧ 2\log_{10} 10$$ \(\small \log_{10} 2\)は正なので、 $$n ≧ \frac{2\log_{10} 10}{\log_{10} 2}$$ ここで、\(\small \log_{10} 10=1\)なので(日本語訳すると、10を何乗したら10になるかという数字なので、答えは1乗)、 $$n ≧ \frac{2}{\log_{10} 2}$$ \(\small \log_{10} 2=0.301\)なので、代入すると $$n ≧ \frac{2}{0.301}$$ $$n ≧ 6.64…$$ 分裂回数は自然数なので、7回目の分裂で大腸菌数が1万をこえることになる。よって、7回の分裂にかかる時間は、20分が\(\small \frac{1}{3}\)時間なので、\(\small \frac{7}{3}\)時間、つまり、2時間20分である。
(解答)2時間20分後







コメント