【保存版】三角比の拡張（0°〜360°）を暗記帳で完全マスター｜90°を超える三角比の覚え方まとめ

三角比の拡張（0°〜360°）で、sin・cos・tan の値を素早く判断できますか？

高校数学の数Ⅱでは、三角関数の方程式や不等式、最大値・最小値を求める問題など、ほぼすべての問題で0°～360°の三角比を素早く正確に求める力が非常に重要になります。

本記事では、0°〜360°の代表角の三角比を単語帳形式（暗記帳）で整理し、効率よく覚えられるようにまとめました。単位円の考え方とセットで練習することで、テストでも瞬時に値を判断できる実力が身につきます。

通学中やスキマ時間に繰り返し確認し、三角比の拡張を確実にマスターしましょう。

　本記事はこんな人におすすめ

三角比（0〜360°）の符号や値をすぐ忘れてしまう人
定期テスト前に「とにかく効率よく」三角比を覚えたい人
三角比の値を単位円上（第1〜4象限）でイメージができず、丸暗記に限界を感じている人

　本記事のレベル

重要度

低

余力あれば

普通

必須

高
難易度

易しい

易

やや易

やや難

難

難しい
暗記/理解

暗記重視

暗記

半々

理解

理解重視

【基礎講義】三角比の拡張（0°～360°）の求め方と覚え方
1. 90°を超える三角比の求め方と覚え方（象限で判断）
【問題演習】三角比（sin・cos・tan）暗記帳｜0°〜360°を一気にマスターしよう
本記事のまとめ

【基礎講義】三角比の拡張（0°～360°）の求め方と覚え方

三角比は代表角だけでも、$\small 0$, $\small \displaystyle \frac{\pi}{6}$, $\small \displaystyle \frac{\pi}{4}$, $\small \displaystyle \frac{\pi}{3}$, $\small \displaystyle \frac{\pi}{2}$, $\small \pi$, $\small 2\pi$ の7種類もあり、さらにそれぞれについて$\small \sin, \cos, \tan$の3種類があるので、覚える量が多すぎて挫折したくなってしまいますよね…。そこにさらに追い打ちをかけるように、三角比の角度が90°を超えて360°まで拡張され…(-_-;)。

でも、実は三角比は単位円を使えば簡単に計算することができます。ここでは90°～360°の角度に対して単位円を活用した三角比の求め方を解説します。そもそも30°、45°、60°の三角比を忘れてしまった人は、三角比って何を表すもの？サイン、コサイン、タンジェントの意味と日常生活での身近な使用例の記事で解説しているので復習から始めましょう。

90°を超える三角比の求め方と覚え方（象限で判断）

90°を超えるの三角比は0°～90°までの三角比だけ覚えておけば、各象限ごとに単位円を活用することで簡単に求めることが可能です。

単位円を用いた三角比（0°～360°）の求め方

・STEP1：単位円上に角度をプロット
・STEP2：0°～90°の三角形を特定
　　　　　※斜辺と$\small x$軸を2辺に持つ三角形に注意！
・STEP3：符号に注意して三角形の辺の比を求める
　　　　　☆$\small \pi$または$\small 2\pi$（※）との差分の角度に着目
　　　　　※象限によって異なる
・STEP4：三角比（sin,cos,tan）に応じた値を計算

手順だけだと分からないと思うので、具体的な例題で解説します。

第2象限｜90°～180°の三角比の求め方

【例題】
$\small \displaystyle \cos \frac{2}{3}\pi$の値を求めてみよう。

【解答】

STEP

単位円上に角度をプロット

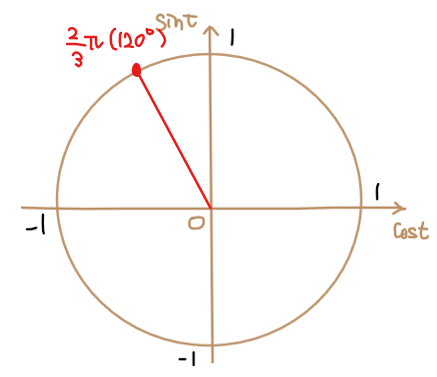
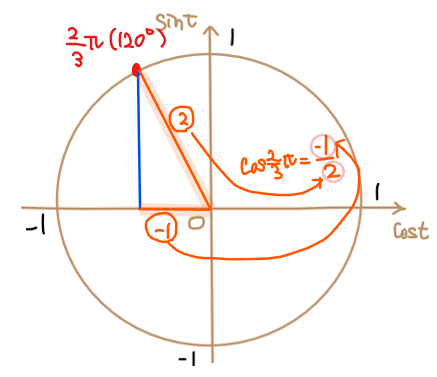
まずは単位円上で角度 $\small \displaystyle \frac{2}{3}\pi$の位置を図示します。

STEP

0°～90°の三角形を特定

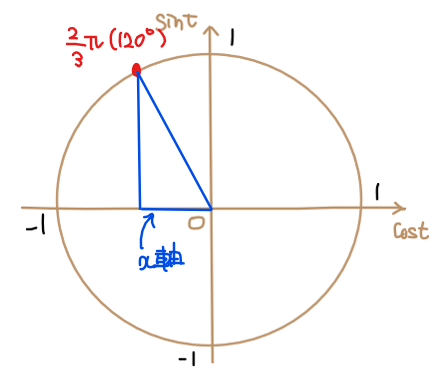
STEP1で角度をプロットすると、$\small x$軸と斜辺を2辺に持つ三角形（下図青色）が見えてきます [*1]。

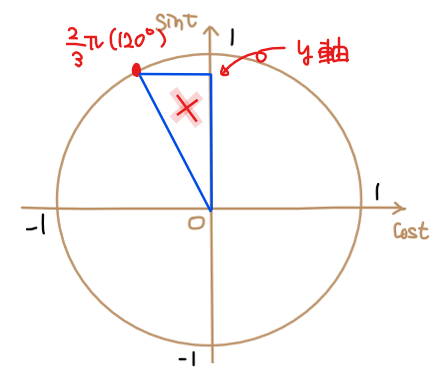
*1：【補足】三角形の書き間違えに注意
斜辺と$\small y$軸を2辺に持つ三角形をかかないように注意。
慣れれば間違えることはなくなりますが、はじめのうちは注意しましょう。

STEP

符号に注意して三角形の辺の比を求める

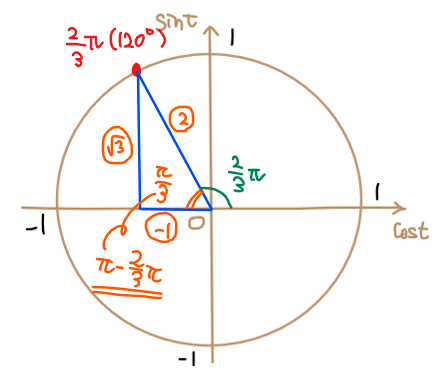
STEP2で特定した青色の三角形は、角度が$\small \displaystyle \frac{\pi}{3}$（=60°）の三角形になっています [*2]。

*2：【補足】なぜ「$\small \pi$ や $\small 2\pi$との差分の角度（補角）」に着目するのか？
STEP3で考えている三角形をよく見ると、もともとは$\small \displaystyle \frac{2}{3}\pi$（120°）の三角比を求める問題だったのが、$\small \displaystyle \frac{\pi}{3}$（60°）の三角比を求める問題に置き換わっていることが分かります。

ここで登場する$\small \displaystyle \frac{\pi}{3}$は、
$$\small \displaystyle \frac{2}{3}\pi=\color{#ef5350}{\pi-\frac{\pi}{3}}$$
のように$\small \pi$との差分（＝補角）にあたる角度になっています。

●補角を使うメリット
90°を超える角度の三角比を求めるとき、その角度の補角は必ず 0°〜90°の範囲におさまります。つまり、補角をイメージできれば、
　・30°の三角比を使うのか
　・45°の三角比を使うのか
　・60°の三角比を使うのか
を素早く判断できるようになります。
（これは慣れが大事なので、演習を重ねるのが一番！）

●$\small 2\pi$との差分を見る場合
$\small 2\pi$との差分の角度を使うのは、角度が 270°〜360° の三角比を求めるときです。

●結論：補角を使えば「必ず 0°〜90°に落とし込める」
補角（または$\small 2\pi$との角度差）を考えることで、すべての角度を 0°〜90° の三角形の三角比の計算に帰着できます。

つまり、0°〜90°までの基本的な三角比だけ覚えておけば、90°以上の三角比もすべて求められるというわけです。

よって、各辺の比は$\small x$座標が負であることに注意すると、$\small -1:2:\sqrt{3}$となります [*3]。

*3：【補足】三角形の辺の比の符号
辺の比を考えるときは$\small x$座標と$\small y$座標の符号に合わせて辺の比の符号を設定してあげましょう。斜辺は円の半径なので常に正になります。

STEP

三角比（sin,cos,tan）に応じた値を計算

あとはコサインに該当する辺の位置関係から$\small \displaystyle \cos \frac{2}{3}\pi=-\frac{1}{2}$ …【答】と求めることができます。

第3象限｜180°～270°の三角比の求め方

求め方・考え方は90°～180°のときと同じです。大きく異なるのは、STEP2の三角形の位置になるので、ここでは三角比を求めるために必要なSTEP2の三角形がどこに該当するのかを単位円上に図示だけします。

【例題2】
$\small \displaystyle \sin \frac{5}{4}\pi$の値を求めてみよう。

【解答】$\small \displaystyle -\frac{1}{\sqrt{2}}$

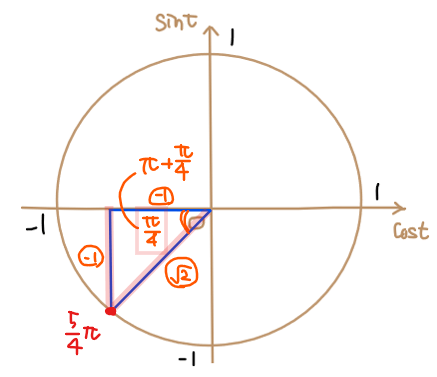
$\small \displaystyle \frac{5}{4}\pi = \color{#ef5350}{\pi + \frac{\pi}{4}}$のように分解できます。　◀$\small \pi$との差分に着目
STEP2の三角形は$\small x$軸と斜辺を2辺に持つ三角形なので下図のようになります。

第4象限｜270°～360°の三角比の求め方

こちらも求め方・考え方は90°～180°のときと同じです。

【例題3】
$\small \displaystyle \tan \frac{11}{6}\pi$の値を求めてみよう。

【解答】$\small \displaystyle -\frac{1}{\sqrt{3}}$

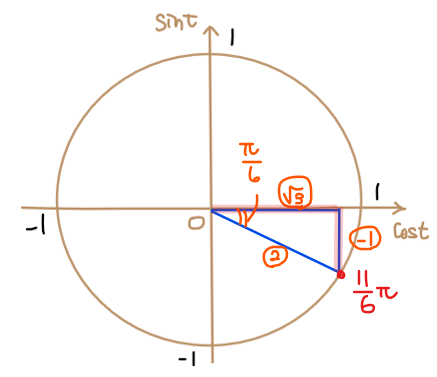
$\small \displaystyle \frac{11}{6}\pi = \color{#ef5350}{2\pi – \frac{\pi}{6}}$のように分解できます。　◀$\small 2\pi$との差分に着目

【問題演習】三角比（sin・cos・tan）暗記帳｜0°〜360°を一気にマスターしよう

ここからは、三角比を効率よく覚えるための単語帳（暗記帳）形式の演習パートです。
sin・cos・tan のそれぞれについて、0°〜360°の代表角をすべて網羅しているので、三角比の値を瞬時に判断できる力を身につけていきましょう。

基礎講義で解説した単位円のイメージを思い浮かべながら、素早く答えられるようになるまで繰り返し練習してみてください。

【sin（サイン）編】0°〜360°の三角比を覚える｜代表角の値まとめ

#各問題をクリックすると解答が表示されます

$\small \displaystyle \sin 0$ の値は？

$\small \displaystyle 0$

$\small \displaystyle \sin \frac{\pi}{6}$ の値は？

$\small \displaystyle \frac{1}{2}$

$\small \displaystyle \sin \frac{\pi}{4}$ の値は？

$\small \displaystyle \frac{1}{\sqrt{2}}$

$\small \displaystyle \sin \frac{\pi}{3}$ の値は？

$\small \displaystyle \frac{\sqrt{3}}{2}$

$\small \displaystyle \sin \frac{\pi}{2}$ の値は？

$\small \displaystyle 1$

$\small \displaystyle \sin \frac{2}{3}\pi$ の値は？

$\small \displaystyle \frac{\sqrt{3}}{2}$

$\small \displaystyle \sin \frac{3}{4}\pi$ の値は？

$\small \displaystyle \frac{1}{\sqrt{2}}$

$\small \displaystyle \sin \frac{5}{6}\pi$ の値は？

$\small \displaystyle \frac{1}{2}$

$\small \displaystyle \sin \pi$ の値は？

$\small \displaystyle 0$

$\small \displaystyle \sin \frac{7}{6}\pi$ の値は？

$\small \displaystyle -\frac{1}{2}$

$\small \displaystyle \sin \frac{5}{4}\pi$ の値は？

$\small \displaystyle -\frac{1}{\sqrt{2}}$

$\small \displaystyle \sin \frac{4}{3}\pi$ の値は？

$\small \displaystyle -\frac{\sqrt{3}}{2}$

$\small \displaystyle \sin \frac{3}{2}\pi$ の値は？

$\small \displaystyle -1$

$\small \displaystyle \sin \frac{5}{3}\pi$ の値は？

$\small \displaystyle -\frac{\sqrt{3}}{2}$

$\small \displaystyle \sin \frac{7}{4}\pi$ の値は？

$\small \displaystyle -\frac{1}{\sqrt{2}}$

$\small \displaystyle \sin \frac{11}{6}\pi$ の値は？

$\small \displaystyle -\frac{1}{2}$

$\small \displaystyle \sin 2\pi$ の値は？

$\small \displaystyle 0$

【cos（コサイン）編】0°〜360°の三角比を覚える｜代表角の値まとめ

#各問題をクリックすると解答が表示されます

$\small \displaystyle \cos 0$ の値は？

$\small \displaystyle 1$

$\small \displaystyle \cos \frac{\pi}{6}$ の値は？

$\small \displaystyle \frac{\sqrt{3}}{2}$

$\small \displaystyle \cos \frac{\pi}{4}$ の値は？

$\small \displaystyle \frac{1}{\sqrt{2}}$

$\small \displaystyle \cos \frac{\pi}{3}$ の値は？

$\small \displaystyle \frac{1}{2}$

$\small \displaystyle \cos \frac{\pi}{2}$ の値は？

$\small \displaystyle 0$

$\small \displaystyle \cos \frac{2}{3}\pi$ の値は？

$\small \displaystyle -\frac{1}{2}$

$\small \displaystyle \cos \frac{3}{4}\pi$ の値は？

$\small \displaystyle -\frac{1}{\sqrt{2}}$

$\small \displaystyle \cos \frac{5}{6}\pi$ の値は？

$\small \displaystyle -\frac{\sqrt{3}}{2}$

$\small \displaystyle \cos \pi$ の値は？

$\small \displaystyle -1$

$\small \displaystyle \cos \frac{7}{6}\pi$ の値は？

$\small \displaystyle -\frac{\sqrt{3}}{2}$

$\small \displaystyle \cos \frac{5}{4}\pi$ の値は？

$\small \displaystyle -\frac{1}{\sqrt{2}}$

$\small \displaystyle \cos \frac{4}{3}\pi$ の値は？

$\small \displaystyle -\frac{1}{2}$

$\small \displaystyle \cos \frac{3}{2}\pi$ の値は？

$\small \displaystyle 0$

$\small \displaystyle \cos \frac{5}{3}\pi$ の値は？

$\small \displaystyle \frac{1}{2}$

$\small \displaystyle \cos \frac{7}{4}\pi$ の値は？

$\small \displaystyle \frac{1}{\sqrt{2}}$

$\small \displaystyle \cos \frac{11}{6}\pi$ の値は？

$\small \displaystyle \frac{\sqrt{3}}{2}$

$\small \displaystyle \cos 2\pi$ の値は？

$\small \displaystyle 1$

【tan（タンジェント）編】0°〜360°の三角比を覚える｜代表角の値まとめ

#各問題をクリックすると解答が表示されます

$\small \displaystyle \tan 0$ の値は？

$\small \displaystyle 0$

$\small \displaystyle \tan \frac{\pi}{6}$ の値は？

$\small \displaystyle \frac{1}{\sqrt{3}}$

$\small \displaystyle \tan \frac{\pi}{4}$ の値は？

$\small \displaystyle 1$

$\small \displaystyle \tan \frac{\pi}{3}$ の値は？

$\small \displaystyle \sqrt{3}$

$\small \displaystyle \tan \frac{\pi}{2}$ の値は？

値なし（定義できない）

$\small \displaystyle \tan \frac{2}{3}\pi$ の値は？

$\small \displaystyle -\sqrt{3}$

$\small \displaystyle \tan \frac{3}{4}\pi$ の値は？

$\small \displaystyle -1$

$\small \displaystyle \tan \frac{5}{6}\pi$ の値は？

$\small \displaystyle -\frac{1}{\sqrt{3}}$

$\small \displaystyle \tan \pi$ の値は？

$\small \displaystyle 0$

$\small \displaystyle \tan \frac{7}{6}\pi$ の値は？

$\small \displaystyle \frac{1}{\sqrt{3}}$

$\small \displaystyle \tan \frac{5}{4}\pi$ の値は？

$\small \displaystyle 1$

$\small \displaystyle \tan \frac{4}{3}\pi$ の値は？

$\small \displaystyle \sqrt{3}$

$\small \displaystyle \tan \frac{3}{2}\pi$ の値は？

値なし（定義できない）

$\small \displaystyle \tan \frac{5}{3}\pi$ の値は？

$\small \displaystyle -\sqrt{3}$

$\small \displaystyle \tan \frac{7}{4}\pi$ の値は？

$\small \displaystyle -1$

$\small \displaystyle \tan \frac{11}{6}\pi$ の値は？

$\small \displaystyle -\frac{1}{\sqrt{3}}$

$\small \displaystyle \tan 2\pi$ の値は？

$\small \displaystyle 0$

本記事のまとめ

今回は、数学Ⅱで学ぶ 三角比（sin・cos・tan）の拡張（0°〜360°）について、単位円の考え方を使いながら「角度ごとの求め方」と「覚え方のコツ」を解説しました。

三角比は 90° を超えるとどの象限に角度があるかによって、0°～90°の三角形の位置や三角比の符号が変わるため、単位円上の三角形の位置を正しくイメージできることが重要なポイントになります。

また、記事後半では 暗記帳（単語帳）形式で、代表角の sin・cos・tan を繰り返し学べるようにしています。通学時間やスキマ時間に何度も確認することで、値を素早く正確に導ける状態を目指しましょう。

✅ 学習のポイントおさらい
・三角比は単位円を使って位置と符号を判断する
・90°を超える場合は $\small \pi, 2\pi$との差分の角に着目して0°～90°の三角形に帰着させて考える
・三角比を覚えるには単位円をイメージする反復練習が最重要

三角比は三角関数につながる非常に大切な分野です。ぜひ本記事の暗記帳を活用しながら、0°～360°の三角比をスムーズに求められる力を身につけていきましょう！

今回はここまでです。お疲れさまでした！