【数Ⅱ】微分係数と導関数の違いとは？定義・意味・求め方を分かりやすく解説

今回は微分係数と導関数の定義と意味、両者の違いについて分かりやすく解説します。また、微分係数の求め方や『導関数の定義に従って関数を微分せよ』という問題の解き方についても解説していますので、苦手な人は本記事で疑問を解消していきましょう！

微分係数・導関数とは？
微分係数・導関数の求め方
1. 【問題1】微分係数の計算
2. 【問題2】導関数の計算
本記事のまとめ

微分係数・導関数とは？

微分係数の意味

中学数学の1次関数の分野で「変化の割合」という用語が出てきたのを覚えていますか？

変化の割合とは

$\small \displaystyle \color{#ff0055}{\frac{yの増加量}{xの増加量}\quad}$を変化の割合と呼ぶ。

これまでの数学では、関数がどれだけ増えたか・減ったかを、ある区間における$\small x$と $\small y$の増加量を考えることで求めてきました。

例えば、関数 $\small y=x^2$において、$\small x=1$～$\small x=3$の区間での変化の割合は、

\begin{split}
&\small \displaystyle \frac{3^2-1^2}{3-1} \\
&\small =\frac{9-1}{2}\\
&\small =4
\end{split}

と求めることができます。

ここで押さえておきたいのは、変化の割合を求めるときは、必ず$\small x$の値が「どこからどこまでか」という区間が指定されているという点です。区間が定まらなければ、$\small x$や$\small y$の変化量が分からないため、変化の割合を求めることはできません。

では、区間ではなく、ある1点での瞬間的な変化の割合を知りたい場合はどうすればよいのでしょうか？

実は、このような「ある瞬間での変化の割合」を考えたものが、微分係数です。もう少し数学的に言うと、変化の割合が関数の平均的な変化量を表すのに対し、微分係数は瞬間的な変化量を表します。

ここで重要となる「平均」と「瞬間」の違いについて理解を深めるために、「平均の速さ」と「瞬間の速さ」という身近な例を考えてみましょう。

例えば、Aさんが家から学校までの1kmの道のりを15分で歩いたとします。このときのAさんの平均の速さは、
$$\small \displaystyle 1（\mathrm{km}）÷ \frac{15}{60}（時間）=4（\mathrm{km}/時）$$
となります。

平均の速さの特徴は、あくまで「平均」であるという点です。実際には、ずっと時速4kmで歩いていたわけではありません。途中で信号待ちのために立ち止まったり、下り坂で歩く速さが速くなったりしたこともあるでしょう。しかし、それらをすべてならして考え、「ずっと同じ速さで歩いていた」と仮定すると時速4kmになる、これが平均の速さの正しい意味になります。

一方で、歩き始めてから5分後にAさんが信号待ちで止まっていたとします。このときの速さは時速0kmです。これが5分時点での瞬間の速さになります。

瞬間の速さは、どの時点を見るかによって変わります。開始5分後は時速0kmであっても、開始10分後には時速5kmで歩いている、ということも十分にあり得ます。このように、ある一時点での速さを表したものが瞬間の速さです。

このような平均の速さと瞬間の速さの例と同様に、平均的な変化を表したものが変化の割合であり、それを瞬間的に捉えたものが微分係数となります。

Point：微分係数とは

ある瞬間での変化の割合のこと。

微分係数の定義

微分係数は

$$\small \displaystyle f^\prime(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$$

と定義されます。微分係数の定義は丸暗記するのではなく、式の意味を理解することが重要です。

まず、右辺の $\small \displaystyle \frac{f(a+h)-f(a)}{h}$部分の意味から考えていきましょう。下図ように、区間 $\small a≦x≦a+h$における関数 $\small y=f(x)$を考えます。

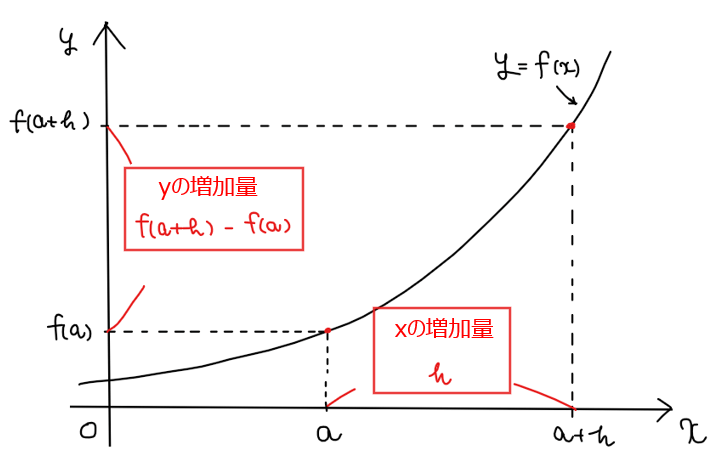
$\small x=a$のときの$\small y$座標は関数 $\small y=f(x)$に$\small x=a$を代入することで$\small y=f(a)$と求まります。同様に、$\small x=a+h$のときの$\small y$座標は$\small y=f(a+h)$です。

すると、$\small \displaystyle \frac{f(a+h)-f(a)}{h}$の分母 $\small h$は、$\small x$の増加量

\begin{split}
\small (a+h)-a=h
\end{split}

になっています。同様に、$\small \displaystyle \frac{f(a+h)-f(a)}{h}$の分子 $\small f(a+h)-f(a)$は、$\small y$の増加量

\begin{split}
\small f(a+h)-f(a)
\end{split}

になっています。

つまり、一見複雑そうに見える$\small \displaystyle \frac{f(a+h)-f(a)}{h}$は、関数 $\small y=f(x)$の変化の割合を求める式になっています。

次に、$\small \displaystyle \lim_{h \to 0}$の意味について考えます。$\small \displaystyle \lim_{h \to 0}$は、「$\small h$を限りなく$\small 0$に近づける」という意味です。このとき、最初に考えた区間 $\small a≦x≦a+h$は、$\small \displaystyle \lim_{h \to 0}$では$\small a≦x≦a$、すなわち$\small x=a$という1点になります。$\small h$は区間の幅だったので、限りなく0に近づく極限では1点になるというのは感覚的にも理解しやすいでしょう。

よって、$\small \displaystyle \frac{f(a+h)-f(a)}{h}$が変化の割合を表していること、そして$\small \displaystyle \lim_{h \to 0}$が区間の幅$\small h$を次第に小さくし、$\small x=a$という1点に近づけていく操作であること、この2つの意味を組み合わせると、、微分係数の定義式は『区間の幅$\small h$を0に限りなく近づけたときの$\small x=a$における関数の変化の割合を表す式』であることが理解できます。

最後に、微分係数の表記 $\small f^\prime(a)$については、$\small f^\prime$という部分で関数$\small f(x)$の変化の割合であることを表し、引数の$\small a$で$\small x=a$での瞬間的な変化の割合だということを表しています。

Point：微分係数の定義

区間の幅 $\small h$を限りなく0に近づけたときの$\small x=a$（＝ある瞬間）における変化の割合は $$\small \displaystyle \color{#ff0055}{f^\prime (a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}}$$ と表され、これを$\small x=a$での微分係数という。

これは、微分係数が『ある瞬間での変化の割合である』という前章で確認した微分係数の意味とも一致していることが分かります。

導関数の定義

$\small x=a$での微分係数は$\small f^\prime (a)$と表されるわけですが、これはある1点での変化量（瞬間的な変化量）なので、どの点を見るかによって微分係数の値は変わってきます（瞬間の速さが開始から何分後かで変わるのと同じ）。

ということは、$\small x$座標の値に応じて微分係数の値が変わるわけですから、微分係数を$\small x$の関数として考えることができることを意味しています。このように微分係数を関数として考えたものを導関数と言います。

微分係数を関数として考えるという部分が少し分かりにくいと思うので、具体例で考えてみましょう。例えば関数 $\small f(x)=x^2$について$\small x=0,1,2,\cdots, 5$のときの微分係数をそれぞれ計算してみましょう。

$\small x=a$のときの微分係数は、微分係数の定義から
\begin{split}
\small \displaystyle f^\prime (a) &\small = \lim_{h \to 0}\frac{f(a+h)-f(a)}{h}\\
&\small = \lim_{h \to 0}\frac{(a+h)^2-a^2}{h} \space \color{#ef5350}{◀f(x)=x^2に代入}\\
&\small = \lim_{h \to 0}\frac{(a^2+2ah+h^2)-a^2}{h}\\
&\small = \lim_{h \to 0}\frac{2ah+h^2}{h}\\
&\small = \lim_{h \to 0}(2a+h) \space \color{#ef5350}{◀hで約分した}\\
&\small =2a\\
\end{split}
となるので、それぞれの値での微分係数は、$\small f^\prime(a)$の$\small a$に$\small 0,1,\cdots, 5$を代入することで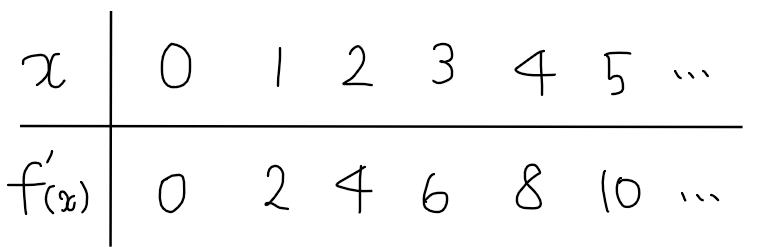

となります。

この関係を見ると、$\small x$の値を2倍したものが微分係数の値になっているので、微分係数は$\small y=2x$という関数で表すことができます。これが微分係数を関数として表すことができるという意味です。

補足

$\small f^\prime(a)=2a$は$\small x=a$という特定の$\small x$座標に対して微分係数の値が$\small 2a$になるという意味ですが、この$\small a$の値を変数（いろいろな値を代入できる文字）と見なしてあげることで微分係数を関数化することができると考えてもOKです。

微分係数は$\small x=a$という特定の$\small x$座標での変化量でしたが、導関数は変化量が変数$\small x$の値によって変わる関数になっているので、微分係数の$\small f^\prime (a)$の$\small a$の部分を変数$\small x$に置き換えたものになります。

Point：導関数の定義

微分係数を関数化した
$$\small \displaystyle \color{#ff0055}{f^\prime(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}$$
を導関数という。
※微分係数の$\small a$を$\small x$に置き換えた（関数化した）もの

導関数の意味

導関数は微分係数を関数にしたものと説明しました。微分係数はある点における瞬間的な関数の変化量ですから、導関数の意味を無理やり日本語化すると、瞬間的な関数の変化を表す関数となります。少し日本語が複雑で分かりにくいですね…。

はじめはそうなんだ…くらいでいいと思います。このあとの微分という分野で導関数がたくさん出てくるので微分を勉強すると導関数が瞬間的な関数の変化を表す関数だということの意味が少しずつ分かってくると思います。

ここでは、そもそもなぜ導関数を考えるのかという意義的を解説しておきます。微分係数を求めることで、特定の$\small x$座標での関数の変化の割合を計算できるわけですが、多くの場合、特定の$\small x$座標での関数の変化量が分かってもあまり使い道がありません。逆に、「関数の変化量が0となるときの$\small x$座標」であったり、「2つの関数の変化量が同じになるときの$\small x$座標」のように、関数の変化量がとある条件を満たすときの$\small x$座標を求めたいことの方が圧倒的に多いです。

そこで、導関数という関数の変化量を求める関数があれば、知りたい変化量の値を関数に代入することでそのときの$\small x$座標を求めることができて便利です。このような理由で導関数というものが考えられるようになりました。

微分係数と導関数の違い

ここまでの解説を踏まえると、微分係数と導関数の違いは理解できたのではないでしょうか。

Point：微分係数と導関数の違い

・微分係数：特定の$\small x$座標における関数の変化量を表す値
・導関数　：微分係数を関数化したもの、すなわち関数の変化量を表す関数

重要なポイントは、微分係数は「1」や「−3」といった数値であるのに対し、導関数は$\small x$のような文字を含む式（関数）であるという点です。性質も見た目もまったく異なるものなので、両者を混同しないように整理して理解しておきましょう。

微分係数・導関数の求め方

では実際に微分係数や導関数を求める問題を解いていきましょう。

【問題1】微分係数の計算

（1）関数 $\small f(x)=2x^2$について、$\small f^\prime(1)$を求めよ。
（2）関数 $\small f(x)=x^3$について、$\small f^\prime(-2)$を求めよ。
（3）関数 $\small f(x)=x^2-3x$について、$\small f^\prime(a)$を求めよ。

問題解決のKey

微分係数の定義
$$\small \displaystyle f^\prime(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$$
にあてはめて計算していきます。

計算時のポイントとしては、
STEP1： $\small \displaystyle \frac{f(a+h)-f(a)}{h}$を計算
STEP2：分母分子を$\small h$で約分
STEP3： $\small h$に0を代入
の3ステップを意識するとよいでしょう。

　解説（1）

微分係数の定義より

\begin{split}
\small \displaystyle f^\prime(1) &\small=\lim_{h \to 0}\frac{f(1+h)-f(1)}{h} \space \color{#ef5350}{◀ 定義式にa=1を代入}\\
&\small \displaystyle =\lim_{h \to 0}\frac{2(1+h)^2-2\cdot1^2}{h} \space \color{#ef5350}{◀ f(x)=2x^2を代入}\\
&\small \displaystyle =\lim_{h \to 0}\frac{2(1+2h+h^2)-2}{h}\space \color{#ef5350}{◀ \mathsf{STEP1}（計算）}\\
&\small \displaystyle =\lim_{h \to 0}\frac{4h+2h^2}{h}\\
&\small \displaystyle =\lim_{h \to 0}(4+2h) \space \color{#ef5350}{◀ \mathsf{STEP2}（hで約分）}\\
&\small \displaystyle =4 \space \color{#ef5350}{◀ \mathsf{STEP3}（hに0を代入）}\\
\end{split}

よって、$\small f^\prime(1)=4$…【答】.

補足：$\small \displaystyle \lim_{h \to 0}$で$\small h=0$を代入してよい理由

微分係数の計算に出てくる極限 $\small \displaystyle \lim_{h \to 0}$の計算について、$\small h=0$を代入してよい理由について解説します。

例えば極限 $\small \displaystyle \lim_{x \to 1} x$は、『$\small x$が$\small 1$と異なる値をとりながら限りなく$\small 1$に近づくときの値』という意味です。数を限りなく1に近づけるというのは具体的にどういうことかを考えると、$\small 0.9$よりも$\small 0.99$、さらには$\small 0.999\cdots$の方が1に近づくことからもわかる通り、末尾に9をたくさん付けていくことが数を1に限りなく近づけることだと分かります。よって、末尾に9が無限に続く数が$\small x \to 1$の極限値になります。

このことを考えると、$\small \displaystyle \lim_{x \to 1} x$が1になるのは、末尾に9が無限に続く数ではないので矛盾しているように思えます。ですが、
$$\small \displaystyle \frac{1}{3}=0.333\cdots$$
の両辺を3倍すると
\begin{split}
\small \displaystyle \frac{1}{3} \color{#ff0055}{\times 3} &\small =0.333\cdots \color{#ff0055}{\times 3}\\
\small \Leftrightarrow \space 1 &\small =0.999\cdots \\
\end{split}
となることから、右辺の$\small 0.999\cdots$は末尾に9が無限に続く数、すなわち$\small x \to 1$の極限値であり、左辺は1となっています。つまり、限りなく1に近づけた数と1は数学的に厳密に同じ値になるわけです。これは他の値の極限でも同じになるので、極限をとる値を直接代入してもOKというわけです。

補足：約分してから極限とる理由

微分係数の計算では、約分をしてから$\small h \to 0$の極限をとるという順番が重要です。仮に順番を逆にしてしまうとうまく値を求められません。
例えば、（1）であれば、
\begin{split}
&\small \displaystyle \lim_{h \to 0}\frac{4h+2h^2}{h}\\
\end{split}
の段階で$\small h=0$を代入すると、$\small \displaystyle \frac{0}{0}$となってしまい、分母に0が来てしまうので数学的に計算不可となってしまいます。ちなみに、$\small \displaystyle \frac{0}{0}=1$ではないので注意しましょう。これは、
\begin{cases}
\small \displaystyle \lim_{h \to 0}\frac{2h}{h}\\
\small \displaystyle \lim_{h \to 0}\frac{3h}{h}\\
\end{cases}
という2つの極限があった場合、どちらもそのまま$\small h \to 0$の極限をとると、$\small \displaystyle \frac{0}{0}$ですが、約分してから極限をとると上側の式は2、下側の式は3となり、1にはなりません。
このように、$\small \displaystyle \frac{0}{0}$というのはどんな値になるかまだ分からない状態（数学的には不定形と言います）なので、しっかりと約分して分母に0が来ないような形にしてから極限をとる必要があります。そのため、約分⇒極限という順番で計算することが大事になります。

　解説（2）

微分係数の定義より

\begin{split}
\small \displaystyle f^\prime(-2) &\small=\lim_{h \to 0}\frac{f(-2+h)-f(-2)}{h} \space \color{#ef5350}{◀ 定義式にa=-2を代入}\\
&\small \displaystyle =\lim_{h \to 0}\frac{(h-2)^3-(-2)^3}{h} \space \color{#ef5350}{◀ f(x)=x^3を代入}\\
&\small \displaystyle =\lim_{h \to 0}\frac{(h^3-6h^2+12h-8)-(-8)}{h}\space \color{#ef5350}{◀ \mathsf{STEP1}（計算）}\\
&\small \displaystyle =\lim_{h \to 0}\frac{h^3-6h^2+12h}{h}\\
&\small \displaystyle =\lim_{h \to 0}(h^2-6h+12) \space \color{#ef5350}{◀ \mathsf{STEP2}（hで約分）}\\
&\small \displaystyle =12 \space \color{#ef5350}{◀ \mathsf{STEP3}（hに0を代入）}\\
\end{split}

よって、$\small f^\prime(-2)=12$…【答】.

　解説（3）

文字が含まれていても解き方は同じです。微分係数の定義より

\begin{split}
\small \displaystyle f^\prime(a) &\small=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}\\
&\small \displaystyle =\lim_{h \to 0}\frac{(a+h)^2-3(a+h)-(a^2-3a)}{h} \space \color{#ef5350}{◀ f(a+h)はxをa+hに置き換え}\\
&\small \displaystyle =\lim_{h \to 0}\frac{h^2+2ah+a^2-3a-3h-a^2+3a}{h}\space \color{#ef5350}{◀ \mathsf{STEP1}（計算）}\\
&\small \displaystyle =\lim_{h \to 0}\frac{h^2+2ah-3h}{h}\\
&\small \displaystyle =\lim_{h \to 0}(h+2a-3) \space \color{#ef5350}{◀ \mathsf{STEP2}（hで約分）}\\
&\small \displaystyle =2a-3 \space \color{#ef5350}{◀ \mathsf{STEP3}（hに0を代入）}\\
\end{split}

よって、$\small f^\prime(a)=2a-3$…【答】.

【問題2】導関数の計算

関数 $\small f(x)=2x^4$を導関数の定義に従って求めよ。

問題解決のKey

導関数の定義
$$\small \displaystyle f^\prime(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
にあてはめて計算していきます。

　解説

導関数の定義より

\begin{split}
\small \displaystyle f^\prime(x) &\small=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\\
&\small \displaystyle =\lim_{h \to 0}\frac{2(x+h)^4-2x^4}{h}\\
&\small \displaystyle =\lim_{h \to 0}\frac{2(x^4+4hx^3+6h^2x^2+4h^3x+h^4)-2x^4}{h}\\
&\small \displaystyle =\lim_{h \to 0}\frac{8hx^3+12h^2x^2+8h^3x+2h^4}{h}\\
&\small \displaystyle =\lim_{h \to 0}(8x^3+12hx^2+8h^2x+2h^3)\\
&\small \displaystyle =\color{red}{8x^3 \space \cdots 【答】}\\
\end{split}

補足

$\small x^n$の導関数が$\small nx^{n-1}$になることを知っていれば簡単に$\small 8x^3$と求められますが、今回は定義式を使って求める問題でした。微分の計算になれると逆に定義から計算する方が難しく感じるかもしれないですね。そこを狙って、たまに入試に出たりします。

本記事のまとめ

今回は、微分係数と導関数の意味、違いについて解説しました。関数の平均的な変化の割合をある瞬間で考えたものが微分係数であり、微分係数を関数化したものが導関数という整理で覚えるとよいでしょう。

言葉の定義だとイメージしずらい場合は、具体例で覚えるのもおすすめです。

関数 $\small f(x)=x^3$について…
　・導関数　：$\small f^\prime (x)=3x^2$　…関数
　　　　　　　⇒導関数は関数に対して1つだけ。
　・微分係数：$\small x=1$での微分係数は、$\small f^\prime(1)=3$　…数値
　　　　　　　⇒微分係数はどの点での瞬間的な変化量を見るかで値が変わる。

今回は以上です。お疲れさまでした！