3次関数が極値を持つ条件と極値を持たない条件を求める問題の解き方について解説します。3次関数の場合は、極値を持つか持たないかの見極めは判別式を使って求めることができますが、なぜ判別式が使えるのか?どういう場合に判別式を使って解くのかについて確認してきましょう。
・極値を持つ条件・持たない条件を判別式で求める方法
・判別式が使える問題・使えない問題とは?
3次関数が極値を持つ条件と判別式を用いた求め方
そもそも極値とは?
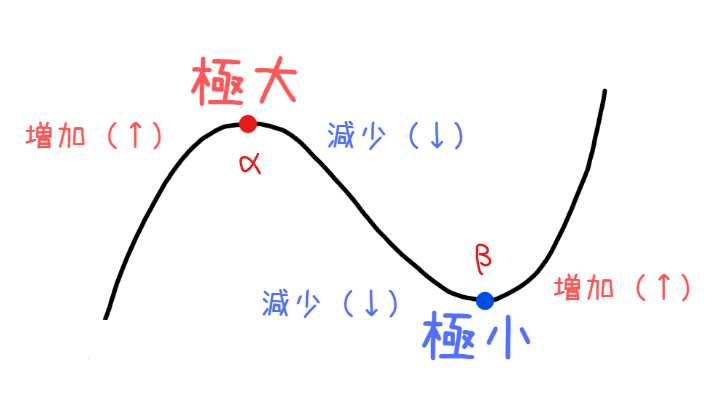
極値とは関数の山と谷のことです。山の部分を極大、谷の部分を極小と言います。
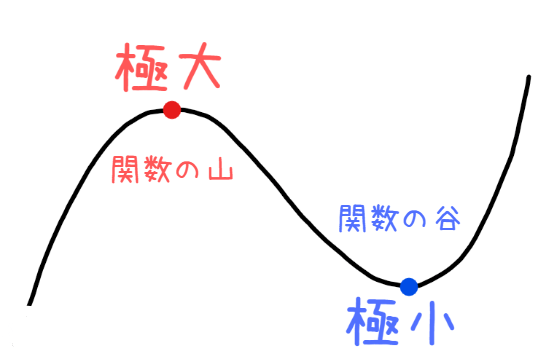
最大(最小)は、関数で「最も」大きい(小さい)場所のことですが、極大(極小)は最大っぽいところ(最小っぽいところ)という違いがあります。例えば、極大よりも大きな値をとる部分はいくらでもあります。
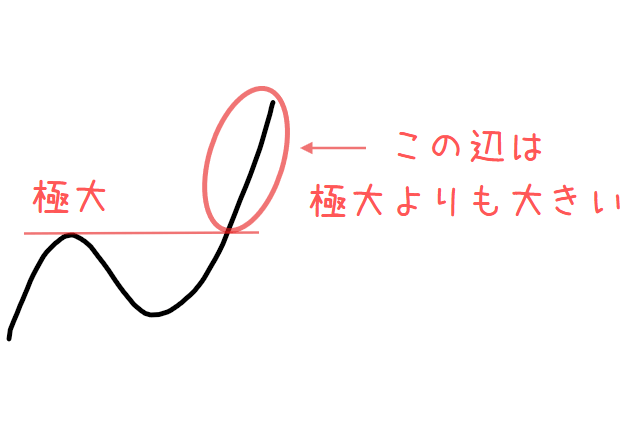
でも狭い範囲で見れば最大っぽい場所だということですね。
なので、極大≠最大(極小≠最小)という点は勘違いしないように注意しましょう!
極値を持つ条件・極値を持たない条件
極値は関数の山と谷なので、極値の前後では関数の上り・下がりが逆転することになります。例えば、極大となる点であれば『上り(↑)から下り(↓)』に変わりますし、極小となる点であれば『下り(↓)から上り(↑)』に変わります。逆に極値以外の点では、関数の上り・下がりに変化はありません。
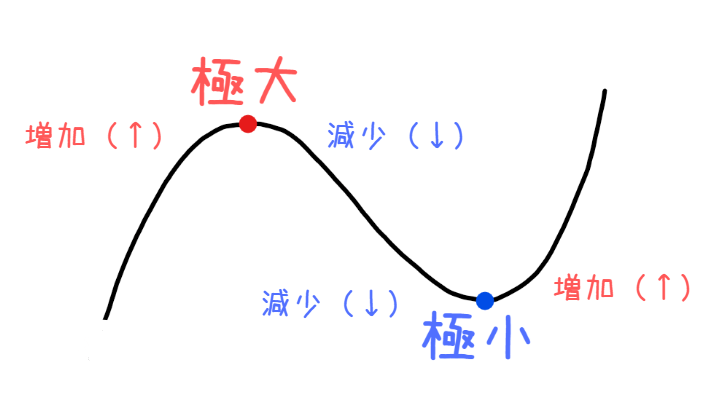
関数の上り・下がりを数学的には関数の増減といいます。なので、関数が極値を持つということは関数の増減が逆転することと言い換えることができます。
また、関数の増減は微分係数の符号で判断できました。なぜならば、微分係数とは関数の接線の傾きを表すからですね。微分係数が正であれば増加、負であれば減少となります。
よって、極値の前後では、関数の増減が変わる ⇔ 微分係数の符号が変わるという特徴があると言えます。この特徴を利用することで、極値を持つか持たないかを以下のように判断できます。
\(\small f^\prime (x)\)は導関数ですが、導関数は微分係数を関数化したものなので、導関数の符号を確認すれば関数の増減を確認できます。
判別式で極値を持つ・持たない条件を求められる理由
どんな関数に対しても極値を持つか持たないかの判断をしたい場合の判定条件は、前章でまとめた通り導関数\(\small f^\prime (x)\)の符号が変わるか否かで判別できます。
特に、3次関数の場合は極値を持つ条件・持たない条件は\(\small f^\prime (x)\)の判別式で判定ができます。
・極値を持つ条件は、\(\small \color{#ff0055}{D>0}\),
・極値を持たない条件は、\(\small \color{#ff0055}{D≦0}\)
なぜ判別式の符号を考えればよいのかについてここからは解説していきます。
まず関数 \(\small f(x)\)が3次関数の場合、\(\small f(x)=ax^3+bx^2+cx+d\)の導関数は微分することで \(\small f^\prime (x)=3ax^2+2bx+c\)と求めることができます。つまり、\(\small f^\prime (x)\)は2次関数になります。ここがポイントです。
この前提知識を踏まえると、3次関数が極値を持つか否かは導関数の符号が変わるか否かで判断できることから、2次関数 \(\small f^\prime(x)\)の符号が変わるか否かを確認すればよいことが分かります。
2次関数 \(\small f^\prime (x)\)の符号は、2次関数と\(\small x\)軸との交点を考えれば判断できます(このあと詳しく解説します)。2次関数と\(\small x\)軸との交点の個数は2次関数の解の個数ですから、判別式の符号に着目して確認していきましょう。
\(\small x\)軸と2点で交わる場合は、交わる前後で必ず符号が変わります。つまり関数は極値を持つことになります。2点で交わる=異なる2つの実数解を持つことと等しいので、判別式は\(\small D>0\)となります。
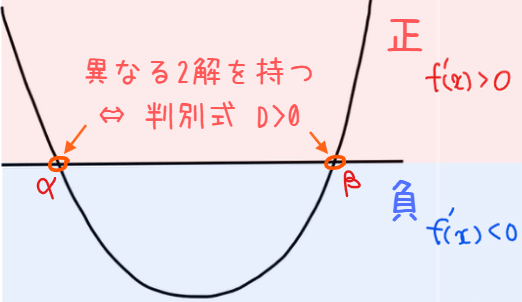
このときの関数 \(\small f(x)\)は \(\small x=\alpha\)で増減が『正→負』になるので極大となり、\(\small x=\beta\)で増減が『負→正』になるので極小となります。
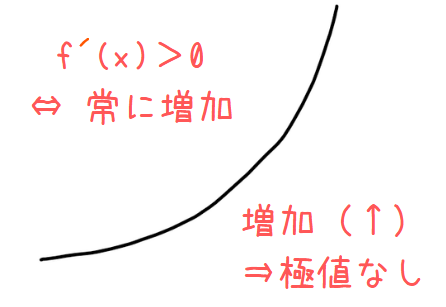
\(\small x\)軸と交わらない場合は、常に正または負になるので符号は変わりません。つまり、関数は極値を持ちません。\(\small x\)軸と交わらない=実数解を持たないので、判別式は\(\small D<0\)となります。

このときの関数 \(\small f(x)\)は増減が常に正になるので常に増加する関数となります。
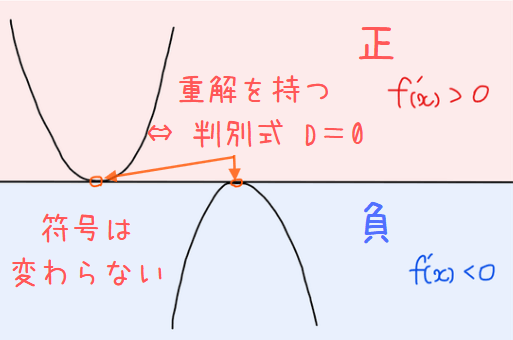
\(\small x\)軸に接する場合は、軸との接点では\(\small f^\prime(x)=0\)になりますが符号が『正→負』または『負→正』に変わることはないので、山や谷を持つことはありません。よって極値も持ちません。この時の判別式は重解を持つ場合のため、\(\small D=0\)です。
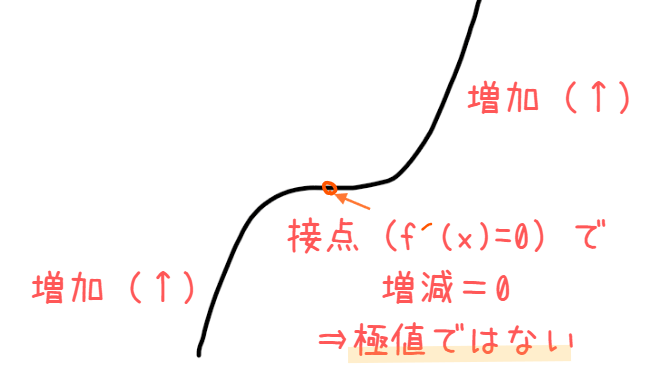
関数 \(\small f(x)\)は接点で一度増減が0になりますが、\(\small f^\prime (x)>0\)となる場合、接点前後での \(\small f^\prime(x)\)の符号は正なので、下図のような増加関数になります。
以上をまとめると、\(\small f^\prime(x)\)の2次関数の判別式が\(\small D>0\)の場合のみ\(\small f^\prime(x)\)の符号が変わるため、極値を持つことが分かります。
判別式が使える問題は?
極値を持つ条件・持たない条件を求めるときに判別式が使えるのは、微分した関数が2次関数だからです。つまり、判別式を使って極値を持つ条件(持たない条件)を求められるのは3次関数の場合だけになります。どんな関数に対しても判別式が使えるわけではないので注意しましょう。
【問題・解説編】極値を持つ条件・持たない条件
【問題1】極値を持たない関数の判別式の条件
関数 \(\small f(x)=2x^3+kx^2+kx+1\)が極値を持たないような定数\(\small k\)の値の範囲を求めよ。
[千葉工大]
・\(\small f^\prime (x)\)の判別式が、\(\small D≦0\)を満たすことを利用して\(\small k\)の範囲を求めよう。
\begin{split}
\small f^\prime (x)= 6x^2+2kx+k
\end{split}
関数の極値は\(\small f^\prime (x)=0\)の解を求めることで求まりますが、今回は極値がないような場合を考える必要があります。つまり
\begin{split}
&\small f^\prime (x) =0\\
\small \Leftrightarrow \space 6x^2 &\small +2kx+k = 0 \space \cdots (*)\\
\end{split}
の解がどんな場合に極値を持たないかを考えていきます。
2次方程式 \(\small (*)\)の解は
(i) 2つの異なる実数解を持つ(判別式 \(\small D>0\))
(ii) 重解を持つ(判別式 \(\small D=0\))
(iii) 実数解を持たない(判別式 \(\small D<0\))
の3パターンなので、それぞれに場合分けして考えていきます。
(i) 2つの異なる実数解を持つ場合
実数解の点で極値を持ってしまうので不適。
(ii) 重解を持つ場合
重解で\(\small f^\prime (x)=0\)となりますが、重解の前後で \(\small f^\prime (x)\)の符号が変わらないため極値にはなりません。よって、極値なしとなります。
(iii) 実数解を持たない場合
解がなければ極値も持たないので、極値なしです。
以上より、条件を満たすのは、\(\small (*)\)が重解を持つ、または実数解を持たない場合なので、このとき判別式が満たす条件より
\begin{split}
&\small \displaystyle \frac{D}{4} ≦0 \quad [*1]\\
\small \Leftrightarrow \space &\small k^2-6\cdot k ≦0\\
\small \Leftrightarrow \space &\small k(k-6) ≦0\\
\small ∴ \space &\small \color{red}{0≦k≦6 \space \cdots 【答】}\\
\end{split}

【問題2】極値を持つ関数の判別式の条件
\(\small a\)を定数とする。関数 \(\small f(x)=2x^3-3(a+2)x^2+12ax\)が極値を持つとき
(1)\(\small a\)が満たすべき条件を求めよ。
(2)\(\small f(x)\)の極大値が\(\small 32\)となるとき、\(\small a\)の値を求めよ。
[静岡大]
・どこで極大値をとるのかは、3次関数を図示して確認するとよいでしょう。
\begin{split}
&\small f^\prime (x) =6x^2-6(a+2)x+12a\\
\end{split}
\(\small f(x)\)が極値を持つためには
\begin{split}
&\small f^\prime (x) =0\\
\small \Leftrightarrow \space &\small 6x^2-6(a+2)x+12a =0\\
\end{split}
この2次方程式が2つの異なる実数解を持てばよいので、判別式が\(\small \displaystyle \frac{D}{4}>0\)を満たせばOKです。
よって
\begin{split}
&\small \displaystyle \frac{D}{4}>0\\
\small \Leftrightarrow \space &\small \{3(a+2)\}^2-6\cdot 12a >0\\
\small \Leftrightarrow \space &\small 9(a+2)^2-72a >0\\
\small \Leftrightarrow \space &\small (a+2)^2-8a >0\\
\small \Leftrightarrow \space &\small (a^2+4a+4)-8a >0\\
\small \Leftrightarrow \space &\small a^2-4a+4>0\\
\small \Leftrightarrow \space &\small (a-2)^2>0\\
\small ∴ \space &\small \color{red}{a \neq 2 \space \cdots 【答】}\\
\end{split}
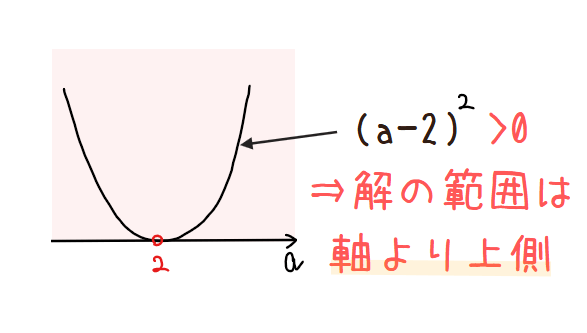
今回は不等式の範囲が『\(\small >0\)』のように正なので軸より上側の範囲が解になりますが、\(\small a=2\)のときだけ軸上となり解の範囲外になるので\(\small a=2\)以外が解となります。
極値を求めるために(1)で計算した\(\small f^\prime (x)=0\)を解くと、
\begin{split}
&\small 6x^2-6(a+2)x+12a =0\\
\small \Leftrightarrow \space &\small x^2-(a+2)x+2a =0\\
\small \Leftrightarrow \space &\small (x-a)(x-2)=0 \quad ◀たすき掛け\\
\small ∴ \space &\small x=a, 2\\
\end{split}
よって、\(\small x=a\)と\(\small x=2\)の2点で極値をとることが分かりました。
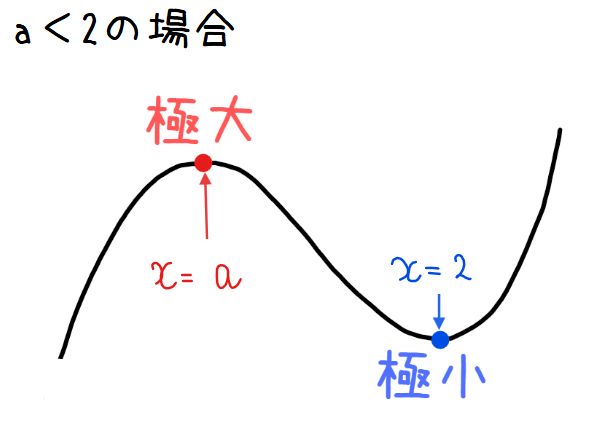
(1)の結果で極値を持つとき、\(\small a\)は\(\small a \neq 2\)を満たすので、\(\small a\)は2以外の値となり極値が1点になることはありません。ただ、\(\small a\)と\(\small 2\)の大小関係までは分からないので、\(\small a<2\) または\(\small 2<a\)の2パターンで場合分けして考える必要があります。
よって、
\begin{split}
&\small f(a) =32\\
\small \Leftrightarrow \space &\small 2a^3-3(a+2)a^2+12a^2=32\\
\small \Leftrightarrow \space &\small 2a^3-3a^3-6a^2+12a^2=32\\
\small \Leftrightarrow \space &\small a^3-6a^2+32=0\\
\small \Leftrightarrow \space &\small (a+2)(a^2 -8a+16)=0 \quad \color{#ef5350}{◀組立除法の利用}\\
\small \Leftrightarrow \space &\small (a+2)(a-4)^2=0\\
\small ∴ \space &\small a=-2, \space 4\\
\end{split}
\(\small a<2\)を満たす解は、\(\small a=-2\) …①
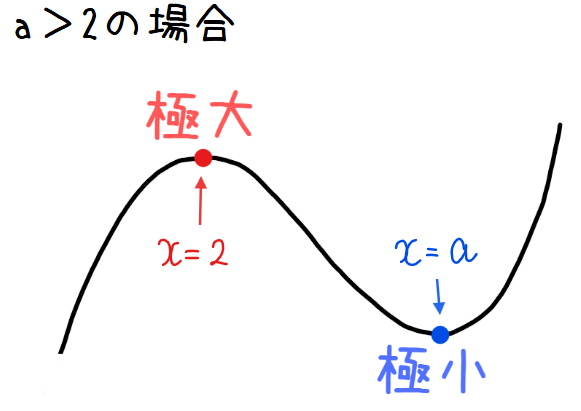
よって、
\begin{split}
&\small f(2) =32\\
\small \Leftrightarrow \space &\small 16-12(a+2)+24a=32\\
\small \Leftrightarrow \space &\small 12a-8=32\\
\small \Leftrightarrow \space &\small 12a=40\\
\small ∴ \space &\small \displaystyle a=\frac{10}{3} \space \cdots ②\\
\end{split}
この解は、\(\small a>2\)も満たしています。
①,②より、\(\small \displaystyle a=-2, \space \frac{10}{3}\)…【答】
今回は以上です。お疲れさまでした!








コメント