「3次方程式の解の個数を調べるときに出てくる定数分離って何?」、「実数解の個数を調べるのに、なぜ増減表やグラフが必要なの?」と感じたことはありませんか?
3次方程式の実数解の個数は、2次方程式のような「判別式」がありません。また、解を直接求めることも非常に困難(一般的には不可能)です。さらに、方程式の問題なのに3次関数のグラフが出てくるため、考え方を理解する段階でつまずきやすいテーマでもあります。
本記事では、数Ⅱ微分の重要テーマである「実数解の個数」について、定期テストや大学入試で頻出の解法2選を徹底解説していきます!
・極値の積(極大値\(\small \times \)極小値)の符号を利用した解法
・「定数分離」と「極値の積の符号」を利用した実数解の個数の求め方・考え方
3次方程式の実数解の個数の求め方2選
【講義1】定数分離|解法手順
・STEP2:関数\(\small y=f(x)\)の概形を図示する
・STEP2-1:\(\small f^\prime (x)=0\)を解いて極値を求める
・STEP2-2:増減表を書く
・STEP3:関数\(\small y=f(x)\)と\(\small y=a\)の交点の個数を調べる
⇒『グラフの交点の個数』=『実数解の個数』
【講義2】定数分離|3次方程式の解の個数が求まる理由
定数分離は、『関数の交点の個数=実数解の個数』という考え方を利用した解法ですが、なぜ関数の交点が方程式の実数解の個数になるのかについて解説しようと思います。
『方程式の解』の個数=『関数の交点』の個数
定数分離の考え方を理解するためには、まず2次関数と直線の交点の個数を求める問題を例に、方程式の解の個数が関数の交点の個数を求めることと同じであるという考え方を理解しておきましょう。
2次関数 \(\small y=x^2\)と直線\(\small y=x+6\)の交点の個数を求めよ。
この問題について、判別式を使わずに具体的な交点の座標を求める解法の流れを追ってみます。
2つの関数 \(\small y=x^2\)と\(\small y=x+6\)を連立して、
\begin{split}
&\small x^2=x+6\\
\small \Leftrightarrow \space &\small x^2-x-6=0\\
\end{split}
という2次方程式を導きます。あとはこの2次方程式を解くことで、交点の\(\small x\)座標は
\begin{split}
\small \Leftrightarrow \space &\small x^2-x-6=0\\
\small \Leftrightarrow \space &\small (x-3)(x+2)=0\\
\small ∴ \space &\small x=-2,3\\
\end{split}
と求まるので、答えは2個になります。
ここで注目してほしいのが、もともとは2次関数と直線の交点の個数を求める問題だったのが、途中から2次方程式の解の個数を求める問題に置き換わっているという点です。なぜ、2次方程式の問題に帰着したのかというと、
2つの関数の交点の座標は、2つの関数をイコールで結んだ方程式の解になるから
です。ということは、この考え方の逆を考えると、
方程式の左辺と右辺を2つの関数と見なせば、方程式の解は2つの関数の交点の座標
になると言えます。
日本語だけだと若干分かりにくいと思うので今回の例題で具体的に考えてみます。\(\small x^2-x-6=0\)という2次方程式があったときに、この方程式を例えば \(\small \color{#ef5350}{x^2}=\color{#5c6bc0}{x+6}\)のように左辺と右辺に分けたとすると、この2次方程式の解は、2次関数 \(\small \color{#ef5350}{y=x^2}\)と直線 \(\small \color{#5c6bc0}{y=x+6}\)の交点の座標になるということです。
この『方程式を左辺と右辺に分ける』方法は、\(\small x^2= x+6\)以外にも、『\(\small x^2-x=6\)』や『\(\small x^2-6=x\)』など複数パターンがあります。分け方によってどんな関数の交点を考えるかは変わりますが、求まる交点自体は同じになります(なぜなら結局解くべき2次方程式は同じだから)。
『3次関数と直線の交点の個数を求める』問題に帰着できる
前置きが長くなりましたが、ここまでの解説で方程式の解の個数は、方程式の左辺と右辺をそれぞれ関数としたときの2つの関数の交点の個数と同じであることを説明しました。
定数分離はこの考え方のうち、方程式を左辺と右辺に分ける分け方が『関数=定数(\(\small f(x)=a\))』と分ける方法のことです。方程式を定数分離することで、関数 \(\small y=f(x)\)と直線 \(\small y=a\)の交点の個数を求める問題に置き換えることができます。
なぜ定数に分けるのかについても補足しておきます。一般的に関数同士の交点の個数はすぐには分かりません。3次関数と斜めの直線の交点とかだとどこで交わるかは具体的な座標を計算しないと把握できないですからね。しかし、方程式の左辺と右辺をどんな分け方をしてもよいという特徴を活かして、右辺を定数にしてあげることで、交点を考える関数が\(\small y=a\)という横一直線の関数(定数関数といいます)になります。横一直線であれば、関数の概形さえ把握しておけば、交点の個数がわかりやすくなります。なので、定数だけ分離するわけです。
まとめると、定数分離とはこれまで学習してきた関数の交点を求める問題の逆の考え方を利用して、方程式を関数と定数に分けることで関数と直線の交点の個数を求め、解の個数を求める方法になります。
特に、右辺が定数になるように分離することで横一直線の定数関数となるため、グラフの交点(=解の個数)を簡単に把握できるようになります。
【講義3】極値の積|解法手順
・STEP2:関数\(\small y=f(x)\)の極値を求める
・STEP2-1: 極値が1個の場合は、実数解の個数は1個
・STEP2-2: 極値が2個の場合は、極値の積の符号に着目
・ 実数解の個数は3個:極値の積が負
・ 実数解の個数は2個:極値の積が0
・ 実数解の個数は1個:極値の積が正
このように置くことで、3次関数 \(\small f(x)=x^3+2x+x+1\)と直線 \(\small y=0\)の交点の個数の問題に帰着できます。
【講義4】極値の積|3次方程式の解の個数が求まる理由
極値の積を利用した解法は3次関数と\(\small x\)軸の交点の個数が3次方程式の解の個数になることを利用した解き方になります(詳しい考え方はこのあとの章で解説します)。
定数分離よりも汎用性が高い解法ですが、その分、定数分離の解法よりも少し考え方が複雑です。
『3次関数とx軸の交点の個数』に着目した解法
講義2で解説した考え方を踏まえると、3次方程式 \(\small f(x)=0\)の解の個数は、3次関数 \(\small y=f(x)\)と直線 \(\small y=0\)との交点の個数と考えることができます。
方程式を左辺と右辺に分ける分け方が定数分離は『関数=定数』でしたが、今回は『関数=0』と分けていきます。
直線 \(\small y=0\)とは\(\small y\)座標が0となる点を集めた直線のことなので、\(\small x\)軸のことです。
つまり、3次方程式 \(\small f(x)=0\)の解の個数は、3次関数 \(\small y=f(x)\)と\(\small x\)軸との交点の個数になります。
極値とx軸の位置関係に着目せよ
3次関数と\(\small x\)軸との交点の個数は、3次関数の極値の位置関係で決まります。
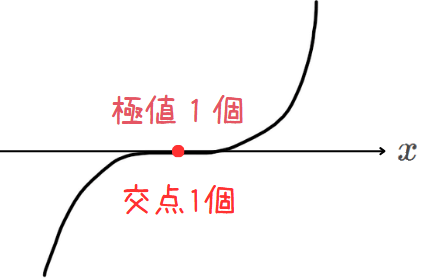
[1] 極値が1個の場合
3次関数と\(\small x\)軸との交点の個数は1個だけ。
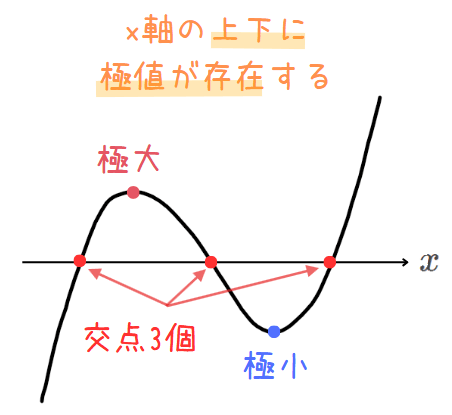
[2] 極値が2個の場合
【パターン①】:\(\small x\)軸との交点の個数が3個の場合
・\(\small x\)軸の上下に極値が存在する。
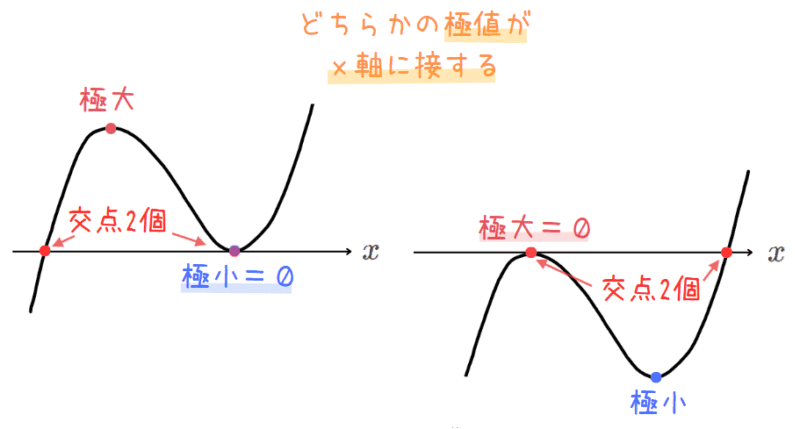
【パターン②】:\(\small x\)軸との交点の個数が2個の場合
・どちらかの極値が\(\small x\)軸に接する。
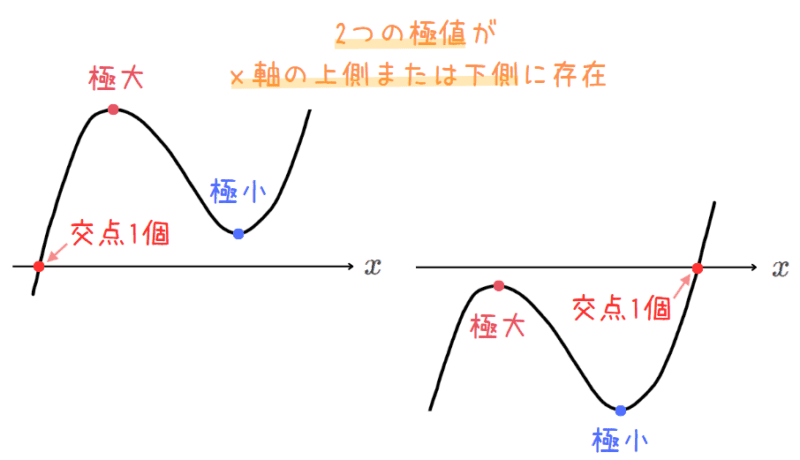
【パターン③】:\(\small x\)軸との交点の個数が1個の場合
・2つの極値が\(\small x\)軸の上側 or 下側に存在する。
極値の積の符号と解の個数
続いて、3次関数と\(\small x\)軸の交点の個数ごとに、極値と\(\small x\)軸の位置関係を条件式として表現できないか考えてみます。
\(\small x\)軸の上側では極値の符号は正、\(\small x\)軸の下側では極値の符号は負、\(\small x\)軸上では極値が0になるという性質に着目すると、極値が2個の場合については、交点の個数は2つの極値の積の符号を用いて次のように判別できます。
【パターン①】:\(\small x\)軸との交点の個数が3個の場合
・\(\small x\)軸の上下に極値が存在する。
⇒極値の符号は正と負
⇒2つの極値の積の符号は負 ※正×負=負
【パターン②】:\(\small x\)軸との交点の個数が2個の場合
・どちらかの極値が\(\small x\)軸に接する。
⇒極値のどちらかが0
⇒2つの極値の積の符号は0 ※●×0=0
【パターン③】:\(\small x\)軸との交点の個数が1個の場合
・2つの極値が\(\small x\)軸の上側 or 下側に存在する。
⇒極値の符号はともに正、またはともに負
⇒2つの極値の積の符号は正 ※正×正=正、負×負=正
一方で、2つの極値の積の符号を考えれば、場合分けせずに1つの条件式で表すことができるので論証が楽になります。
【問題&解説】3次方程式の実数解の個数
【問題1】定数分離
3次方程式 \(\small x^3-2x-a=0\)の異なる実数解の個数は、定数\(\small a\)の値によってどのように変わるか。
$$\small x^3-2x=a$$
のように定数分離します。あとは、左辺を\(\small f(x)=x^3-2x\)とおいて関数 \(\small y=f(x)\)のグラフの概形を図示して、直線 \(\small y=a\)との交点の個数を調べていけばよいでしょう。
\(\small f(x)=x^3-2x\)とおくと、問題の3次方程式は
\begin{split}
\small x^3-2x=a
\end{split}
の形に定数分離できるので、問題の方程式の解の個数は、3次関数 \(\small f(x)=x^3-2x\)と定数関数 \(\small y=a\)の交点の個数を調べる問題に帰着できます。
ではここからは関数 \(\small f(x)\)のグラフの概形を確認していきます。グラフを書くために必要なのは、極値と増減表だったのでそれぞれ確認していきます。
極値を求めるために \(\small f(x)\)の微分を計算すると、
\begin{split}
\small f^\prime (x)=3x^2-2\\
\end{split}
となるので、極値は
\begin{split}
&\small f^\prime (x)=0\\
\small \Leftrightarrow \space &\small 3x^2-2=0\\
\small \Leftrightarrow \space &\small x^2=\frac{2}{3}\\
\small ∴ \space &\small x=\pm \frac{\sqrt{6}}{3}\\
\end{split}
と求められます。
また、増減表は下図のようになります。
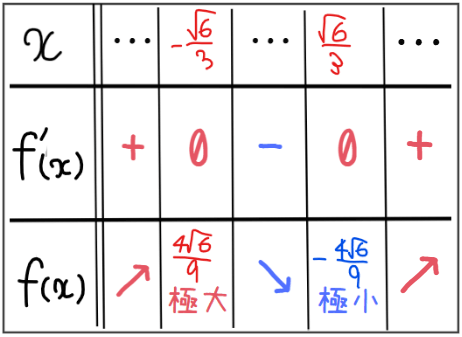
最後に、3次関数 \(\small y=f(x)\)と\(\small y=a\)との位置関係から、交点の個数を求めていきます。
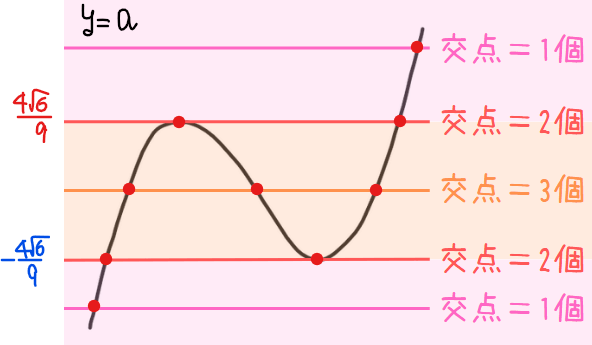
3次関数\(\small y=f(x)\)のグラフの概形は増減表から、上図の黒曲線のようになります。今回は、直線との交点が分かればよいので、極大値 \(\small \displaystyle \frac{4\sqrt{6}}{9}\)、極小値 \(\small \displaystyle -\frac{4\sqrt{6}}{9}\)だけ記載しておけば十分です。
また、横一直線の関数が\(\small y=a\)で、\(\small a\)の値(上下方向の位置)によって交点の個数が図のように異なることが分かります。
よって、3次方程式の実数解の個数は
\begin{split}
\begin{cases}
\small \displaystyle \frac{4\sqrt{6}}{6}< a, \space a<-\frac{4\sqrt{6}}{6}のとき1個,\\
\small \displaystyle a = \pm \frac{4\sqrt{6}}{6}のとき2個,\\
\small \displaystyle -\frac{4\sqrt{6}}{6}< a<\frac{4\sqrt{6}}{6}のとき3個
\end{cases}
\small \quad \cdots 【答】
\end{split}
例えば、関数 \(\small y=a\)が3次関数と3つの交点を持つためには、\(\small \displaystyle -\frac{4\sqrt{6}}{9}<y<\frac{4\sqrt{6}}{9}\)の範囲に直線 \(\small y=a\)があればよいので、\(\small a \)は\(\small \displaystyle -\frac{4\sqrt{6}}{9}<a<\frac{4\sqrt{6}}{9}\)の範囲にあればよいことになります。
【問題2】極値の積の符号
3次方程式 \(\small x^3-3ax^2+a=0\)の異なる実数解の個数は、定数\(\small a\)の値によってどのように変わるか。
$$\small \displaystyle \frac{x^3}{3x^2-1}=a$$
のように定数分離することもできますが、左辺の関数 \(\small \displaystyle f(x)=\frac{x^3}{3x^2-1}\)のグラフの概形が分からないため、直線 \(\small y=a\)との交点の個数をグラフから判断できません(数Ⅲの微分を学習すれば概形を書くことができます)。
このように定数分離をしたときにグラフの概形が把握できない場合は、極値の積の符号に着目して実数解の個数を判断する解法が有効です。
3次方程式の左辺を \(\small f(x)=x^3-3ax^2+a\)とおき、この3次関数の極値の積の符号を考えることで実数解の個数を判別していきます。
なので、まずは3次関数 \(\small f(x)=x^3-3ax^2+a\)の極値を求めていきましょう。
\begin{split}
&\small f^\prime (x)=0 \quad \color{#ef5350}{◀極値ではf^\prime (x)=0}\\
\small \Leftrightarrow \space &\small 3x^2-6ax=0\\
\small \Leftrightarrow \space &\small 3x(x-2a)=0\\
\small ∴ \space &\small x=0, \space 2a\\
\end{split}
ここで、\(\small a=0\)のとき\(\small x=2a=0\)となるため極値は \(\small x=0\)の1点のみになることに注意します。それ以外の\(\small a \neq 0\)の場合は、\(\small x=0\)と\(\small x=2a\)の2点で極値を持つことになります。
2つの極値の積を考えていきたいわけですが、これは極値の個数が2個であることを前提にしているため、極値が1個の場合は特殊ケースとして先に解の個数を確認しておきましょう。
[1] \(\small a=0\)の場合(極値が1個の場合)
このとき\(\small f(x)=x^3\)となり、極値は \(\small x=0\)で\(\small f(0)=0\)であることから、実数解の個数は1個 …①。
[2] \(\small a \neq 0\)の場合(極値が2個の場合)
2つの極値は、
\(\small x=0\)のとき、\(\small f(0)=a\)、
\(\small x=2a\)のとき、\(\small f(2a)=-4a^3+a\)
となります。あとは、関数 \(\small f(x)=x^3-3ax^2+a\)と\(\small x\)軸との交点の個数が実数解の個数になるので、パターンごとに場合分けして確認していけばよいでしょう。
(i)実数解の個数が3個の場合
3次関数 \(\small f(x)=x^3-3ax^2+a\)と\(\small x\)軸との交点の個数が3個になる場合であり、このとき極値は\(\small x\)軸の上下に1個ずつ存在する必要があります。
このとき、2つの極値は異符号になるため、その積は
$$\small \color{#ef5350}{ f(0)f(2a)<0}$$
を満たします。
故に、
\begin{split}
&\small f(0)f(2a)<0\\
\small \Leftrightarrow \space &\small a(-4a^3+a)<0\\
\small \Leftrightarrow \space &\small -a^2(4a^2-1)<0\\
\small \Leftrightarrow \space &\small a^2(2a-1)(2a+1)>0\\
\end{split}
\(\small a \neq 0\)では\(\small a^2 >0\)(2乗した値は正になる)なので、
\begin{split}
&\small (2a-1)(2a+1)>0 \quad \color{#ef5350}{◀2次不等式}\\
\small ∴ \space &\small \displaystyle \color{#ef5350}{a<-\frac{1}{2}, \space \frac{1}{2}<a \quad \cdots ②}\\
\end{split}
(ii)実数解の個数が2個の場合
3次関数 \(\small f(x)=x^3-3ax^2+a\)と\(\small x\)軸との交点の個数が2個になるとき、2つの極値のどちらか一方は\(\small x\)軸に接している必要があります。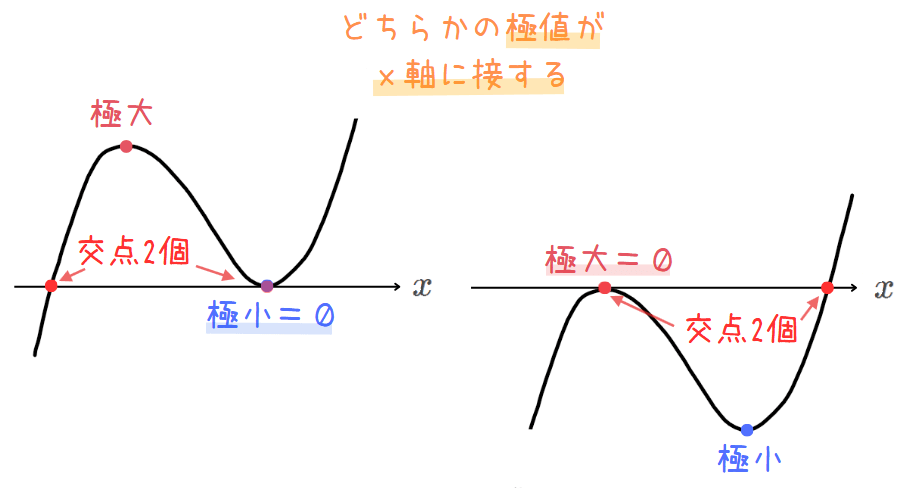
このとき、2つの極値の積は0になるので
\begin{split}
&\small \color{#ef5350}{f(0)f(2a)=0}
\end{split}
の条件を満たします。
故に、
\begin{split}
&\small a(-4a^3+a)=0\\
\small \Leftrightarrow \space &\small a^2(2a-1)(2a+1)=0\\
\small \Leftrightarrow \space &\small \displaystyle a=0, \pm \frac{1}{2}\\
\end{split}
\(\small a \neq 0\)(極値が2個)の場合であることに注意すると、適切な解は、\(\small \displaystyle a =\pm \frac{1}{2}\) …③.
(iii)実数解の個数が1個の場合
3次関数 \(\small f(x)=x^3-3ax^2+a\)と\(\small x\)軸との交点の個数が1個になるとき、2つの極値がどちらも\(\small x\)軸より上側または下側に存在している必要があります。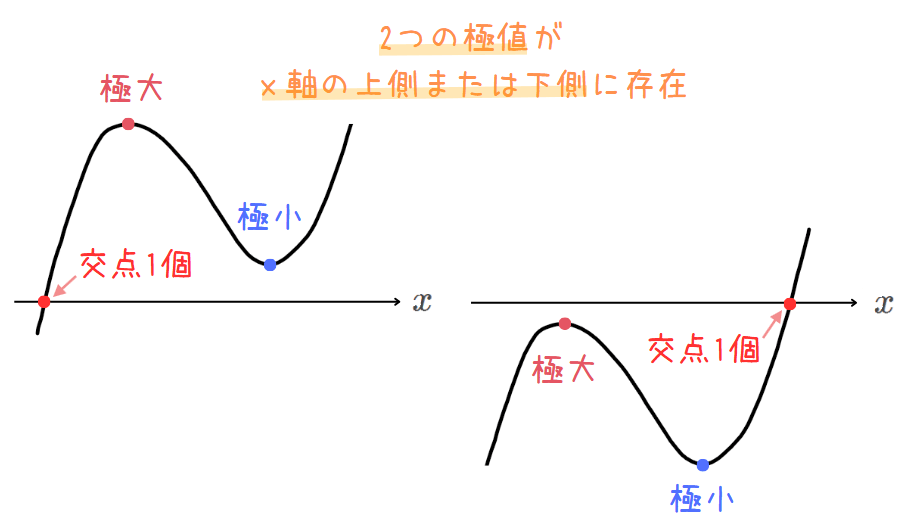
このとき、2つの極値は同符号になることから、その積は
\begin{split}
&\small \color{#ef5350}{f(0)f(2a)>0}
\end{split}
を満たします。
故に、
\begin{split}
&\small a(-4a^3+a)>0\\
\small \Leftrightarrow \space &\small a^2(2a-1)(2a+1)<0\\
\small \Leftrightarrow \space &\small (2a-1)(2a+1)<0 \quad (\space ∴ \space a^2>0)\\
\small \Leftrightarrow \space &\small \displaystyle -\frac{1}{2}<a<\frac{1}{2}\\
\end{split}
\(\small a \neq 0\)より、\(\small \displaystyle \color{#ef5350}{-\frac{1}{2}<a<0, \space 0<a<\frac{1}{2} \space \cdots ④}\).
以上、①~④より
\begin{split}
\begin{cases}
\small \displaystyle -\frac{1}{2}< a<\frac{1}{2}のとき1個,\\
\small \displaystyle a = \pm \frac{1}{2}のとき2個,\\
\small \displaystyle a<-\frac{1}{2}, \space \frac{1}{2}<a のとき3個
\end{cases}
\small \quad \cdots 【答】
\end{split}







コメント