分数を含む群数列の問題は、「規則性は分かるけど、どこからどうやって求めていけば良いのかが分からない…」と感じる人が多いと思います。一方で、問題パターンとしては、「第n群や初項から第100項目までの和を求める問題」や「指定された数が第何群の第何項目かを求める問題」、「第n項目の数を求める問題」くらいであり、パターンごとの考え方のコツさえ一度理解してしまえば、おおかたの問題が一気に解けるようになります。
本記事では、分数を含む群数列について、第n項目・第n群の和の求め方や何番目の項がどの群に属するかの調べ方といった典型問題の解き方を図表付きで分かりやすく解説します。最後まで学習して群数列の苦手意識を克服しましょう!
- 分数を含む群数列の解き方に苦手意識がある人
- 第何群の何項目か求める方法を知りたい人
- 第n群目の和の求め方、第1項目から第n項目までの和の求め方を知りたい人
- 典型問題の解き方の流れを再整理したい人
分数の群数列の典型問題(総和・第何群・何番目)
分数の群数列の典型問題を丸ごと演習できる問題を用意したので、こちらの問題を解くことで考え方や解き方の流れに関する理解を深めていきましょう。
\(\small 2\)の累乗を分母とする既約分数を次のように並べた数列について、以下の問いに答えよ。
$$\small \displaystyle \frac{1}{2}, \frac{1}{4},\frac{3}{4},\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8},\frac{1}{16},\frac{3}{16},\frac{5}{16},\cdots,\frac{15}{16},\frac{1}{32},\cdots$$
(1)分母が\(\small 2^n\)となっている項の和を求めよ。
(2)初項から第\(\small 100\)項までの和を求めよ。
(3)\(\small \displaystyle \frac{101}{256}\)は第何項目か求めよ。
(4)第\(\small 2025\)項目の値を求めよ。
[改 岩手大]
・問題(1)の解答&解説
・問題(2)の解答&解説
・問題(3)の解答&解説
・問題(4)の解答&解説
【問題1】第n群の総和の求め方
\(\small 2\)の累乗を分母とする既約分数を次のように並べた数列
$$\small \displaystyle \frac{1}{2}, \frac{1}{4},\frac{3}{4},\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8},\frac{1}{16},\frac{3}{16},\frac{5}{16},\cdots,\frac{15}{16},\frac{1}{32},\cdots$$
について、分母が\(\small 2^n\)となっている項の和を求めよ。
・第\(\small n\)群の和を求めるには、分子が等差数列になっているという規則性を把握して等差数列の和の公式を用いて解き進めていくのがポイントです。
求めるべき和は、分母は\(\small 2^n\)で一定なので、
\begin{split}
&\small \displaystyle \frac{1}{2^n}+\frac{3}{2^n}+\cdots + \frac{末項}{2^n}\\
&\small \displaystyle =\frac{1+3+\cdots + 末項 \quad }{2^n} \quad \cdots (*)\\
\end{split}
となります。よって、この和を求めたければ、分子の和が求められれば良いことになります。
では、分子の規則性を確認しておきます。たとえば、分母が8の場合で確認すると、先頭から\(\small 1,3,5,7\)となっているので、奇数が小さい順に並んでいることが分かります。
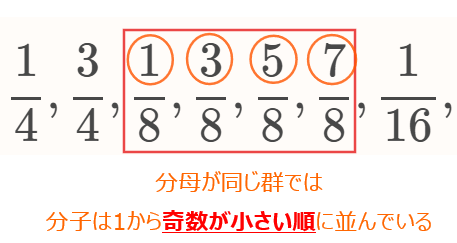
念のため分母が16の場合でも確認しておくと、分子は\(\small 1,3,5,7,9,11,13,15\)となり、群の最後の分数が\(\small \displaystyle \frac{15}{16}\)になるので、予想は当たっていそうです。
ということで、分子の和を求めるには、奇数列 \(\small 1,3,5,\cdots\)の和を求める必要があります。奇数列は初項が1、公差が2の等差数列なので、等差数列の和の公式
\begin{split}
\small \displaystyle S=\dfrac{(初項+末項) \times 項数 \qquad }{2}\\
\end{split}
を用いると
\begin{split}
\small \displaystyle 1+3+\cdots + 末項=\dfrac{(1+末項) \times 項数 \qquad }{2} \cdots ①\\
\end{split}
で求めることができます。
今回であれば、初項は1とすぐに分かりますね。なのであとは末項と項数が分かればOKです。
末項の値について、問題中にある数列を見て規則性がないか確認します。たとえば、分母が\(\small 4\)の群であれば末項は\(\small 3\)、分母が\(\small 8\)の群であれば末項は\(\small 7\)、分母が\(\small 16\)の群であれば末項は\(\small 15\)になっています。これらを見ると、末項は分母の値から1引いた値になっていることが分かります[*1]。
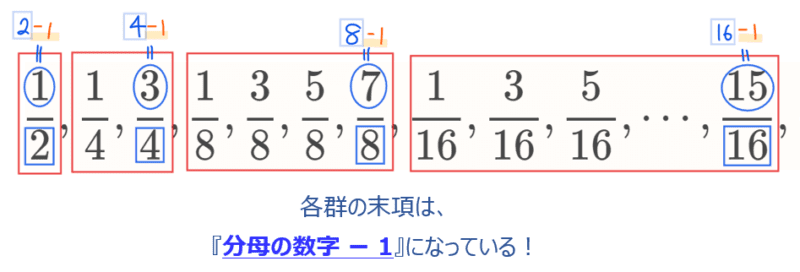
*1:【補足】分子の規則性について
問題文中には明記はないですが、分子の奇数は分母の\(\small 2^n\)を超えない最大の奇数でストップしていることが分かります。このことから、分母が\(\small 2^n\)で必ず偶数なのでそこから1引くと必ず奇数になり、\(\small 2^n-1\)が分母を超えない最大の奇数ということになります。
よって、分母が\(\small 2^n\)の群の末項は\(\small 2^n-1\)…②であることが分かります。
最後に項数ですが、これは\(\small 1,3,5,\cdots\)の奇数列の一般項を求めて、\(\small 2^n-1\)が何項目かを求めれば項数が分かります。
\(\small 1,3,5,\cdots\)の奇数列は初項1、公差2の等差数列なので、一般項 \(\small a_k\)は
\begin{split}
\small a_k &\small = 1+(k-1)\cdot 2\\
&\small = 2k-1\\
\end{split}
よって、第\(\small k\)項が\(\small 2^n-1\)になるような\(\small k\)の値を求めれば\(\small 2^n-1\)が第何項目かが求まるので、\(\small a_k=2^n-1\)を代入して\(\small k\)の値を求めると
\begin{split}
\small 2^n-1 &\small = 2k-1\\
\small \Leftrightarrow \space \small 2k &\small = 2^n\\
\small \Leftrightarrow \space \small k &\small = 2^{n-1}\\
\end{split}
以上より、\(\small 2^n-1\)は奇数列の第\(\small 2^{n-1}\)項目であることが求まったので、分子の\(\small 1,3,5, \cdots , 2^n-1 \)の項数は\(\small 2^{n-1}\)個…③と求められます [*2]。
*2:【補足】項数の計算と検算
文字が多くて考え方が分かりにくいですが、やっていること自体はそれほど難しくはないです。
たとえば、奇数列 \(\small 1,3,5,\cdots ,15\)の項数は何個かを求めたければ、数列の一般項を解説にあるように求めて(\(\small a_k=2k-1\))、求めた一般項が15になるような\(\small k\)の値が分かれば、第何項目かが分かり(\(\small a_k=15\)を代入して\(\small k\)を求めると\(\small k=8\)なので15は第8項目)、15が先頭から第何項目かが分かります。するとそれは15が先頭から何番目の項かを求めたことになるので(今回であれば先頭から8番目の項)、『何番目の項か=項の個数』(8番目の項、すなわち8項目=8個の項がある)となり項の個数が求められるという考え方になります。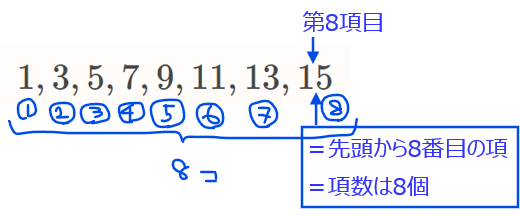
解答では「15」の部分が\(\small 2^n-1\)になっているだけで手順は同じです。照らし合わせながら理解してみてください。
また、求めた項の数 \(\small 2^{n-1}\)があっているのか確認したければ実際に\(\small n=1,2,3\)の場合などで検算して確かめるのが効果的です。\(\small n=2\)の場合は、すなわち分母が\(\small 2^2=4\)の場合では、項数は\(\small 2^{2-1}=2\)個となりますが、実際に問題の数列を見ると\(\small \displaystyle \frac{1}{4}, \frac{3}{4}\)の2個で一致しています。
②、③で求めた末項と項数を①に代入すると
\begin{split}
\small \displaystyle 1+3+\cdots + 末項 &\small =\dfrac{(1+2^n-1)\cdot 2^{n-1}}{2}\\
&\small =\dfrac{ 2^{2n-1}}{2}\\
&\small = 2^{2n-2}\\
\end{split}
これで、\(\small (*)\)の式の分子の和が\(\small 2^{2n-2}\)と求まったので、問題で問われている分母が\(\small 2^n\)の項の和は、\(\small (*)\)に代入することで
\begin{split}
&\small \displaystyle \frac{1+3+\cdots + 末項 \quad }{2^n}\\
&\small \displaystyle =\frac{2^{2n-2}}{2^n}\\
&\small \displaystyle =2^{ \color{#ef5350}{2n-2-n}} \space \color{#ef5350}{◀指数法則 \frac{a^m}{a^n}=a^{m-n}を利用}\\
&\small \displaystyle =\color{red}{2^{n-2} \space \cdots 【答】}\\
\end{split}
【問題2】初項から第n項までの総和の求め方
\(\small 2\)の累乗を分母とする既約分数を次のように並べた数列
$$\small \displaystyle \frac{1}{2}, \frac{1}{4},\frac{3}{4},\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8},\frac{1}{16},\frac{3}{16},\frac{5}{16},\cdots,\frac{15}{16},\frac{1}{32},\cdots$$
について、初項から第\(\small 100\)項までの和を求めよ。
具体的には…
・STEP1:第\(\small k\)項が何群目の何番目かを把握する
・STEP2:『群全部の和(群単位の和)』+『群の途中までの和(端数部分の和)』に分けて和を求める
の2ステップで考えるのが定石。
【研究】なぜ群数列の和には和の公式がないの?
群数列の初項から特定の項までの和の計算は、等差数列や等比数列の和のように、特定の公式があるわけではありません。理由は、群数列の場合群の中での規則性と群を跨ぐときの規則性が異なるため、一定の規則性にならず決まった公式が作れないからです。少し分かりにくいと思うので具体例で補足します。例えば本問の数列であれば、同じ群の中では「分母が\(\small 2^n\)で一定で、分子が奇数列になっており、末項の分子は\(\small 2^n-1\)である」という規則性があることを問題1で確認しました。一方で、群を跨ぐ場合は、例えば第2群の末項 \(\small \displaystyle \frac{3}{4}\)と第3群(分母が8の群)の初項 \(\small \displaystyle \frac{1}{8}\)の間では「分子は3 ⇒ 1に逆戻りし分母も4 ⇒ 8に2倍される」という規則性になっており、群の中での規則性とは異なっています。規則性が常に同じではないので和を計算する公式が作れないわけです。
でもこれって裏を返せば群単位であれば規則性がある=数列の規則性に合わせて等差数列・等比数列等の和の公式が使えるということなので、群単位での和を求めるという考え方につながるわけです。
まずは、第100項が第何群の何番目の項であるかを確認していきます。と言っても、群数列では一般項があるわけではないので、少し面倒です。
まずは第何群にあるかを特定していきます。求めたい第100項目というのは、数列の先頭から100項目に位置するので、第1群(数列の先頭)から第\(\small n\)群までの項数の合計が分かれば\(\small n\)に適当な値を代入して100くらいになるような\(\small n\)を求められます。
第\(\small k\)群の項数は問題1で\(\small 2^{k-1}\)個と求めているので、第1群から第\(\small n\)群までの項数は
\begin{split}
&\small \displaystyle \sum_{k=1}^n 2^{k-1} \quad ◀第1群(k=1)~第n群(k=n)までの項数の和\\
&\small \displaystyle =\frac{2^n-1}{2-1} \quad ◀初項1、公比2の等比数列の和\\
&\small \displaystyle =2^n-1\\
\end{split}
例えば、上式に\(\small n=3\)を代入してみると、第1群から第3群までの合計項数を求めることができて、\(\small 2^3-1=7\)項あることが分かります(実際に数えてみても7項ありますね)。
この式を使って第100項に近くなりそうな\(\small n\)の値を探してみると、
\begin{split}
&\small n=6のとき、第1群~第6群までの項数は、2^6-1=63項、\\
&\small n=7のとき、第1群~第7群までの項数は、2^7-1=127項\\
\end{split}
となり、第7群目に第100項目があることが分かります。
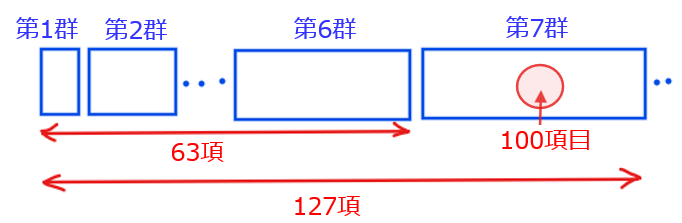
さらに、第6群までで63項あることから、第100項目は第7群の先頭から何番目にあるかを求めると、\(\small 100-63=37\)番目と求めることができます。
まとめると、第100項目は、第7群の37番目に位置することが分かりました。ここまででSTEP1が完了です。
ここからSTEP2として、初項から第100項目の和を求めるために、群単位の和と端数部分の和に分解していきます。
まず、群全部を丸ごと和をとれる部分(ここでは群単位の和と呼称)は、下図より第1群~第6群までで、残りの第7群にある先頭~37番目(第100項目)までの和が端数部分の和になります。
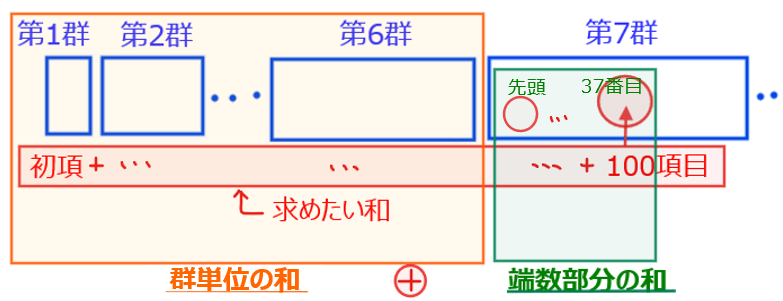
●群単位の和を求めよう
問題1で第\(\small n\)群(分母が\(\small 2^n\)の群)の和が\(\small 2^{n-2}\)であるということを求めたので、この結果を利用して第1群~第6群までの和を求めればよいでしょう。
よって、
\begin{split}
&\small \sum_{k=1}^6 2^{k-2} \space ◀第k群の和2^{k-2}をk=1~6で和をとる\\
&\small \displaystyle =\frac{\dfrac{1}{2}\left(2^6-1\right)}{2-1} \space ◀初項\frac{1}{2},公比2の等比数列の和\\
&\small \displaystyle =\color{#ef5350}{\frac{63}{2} \space \cdots ①}\\
\end{split}
●端数部分の和を求めよう
端数部分の数列を明記すると
$$\small \displaystyle \frac{1}{2^7},\frac{3}{2^7},\frac{5}{2^7},\cdots ,\frac{73}{2^7}$$
となります。第100項目は先頭から37番目の項であり、分子は奇数列\(\small a_k= 2k-1\)(\(\small k\)は先頭から何番目かを表す)になっているので、\(\small k=37\)を代入することで求められます。
よって、端数部分の和は
\begin{split}
&\small \displaystyle \frac{1}{2^7}+\frac{3}{2^7}+\frac{5}{2^7}+\cdots +\frac{73}{2^7}\\
&\small \displaystyle =\frac{1+3+5+\cdots +73}{2^7}
\end{split}
となり、分子の和は等差数列の和なので、
\begin{split}
&\small \displaystyle \frac{(初項+末項) \times 項数 \qquad}{2}
\end{split}
の公式を利用することで、
\begin{split}
\small \displaystyle 1+3+5+\cdots + 73 &\small = \frac{(1+73)\times \color{#ef5350}{37}}{2} \space \color{#ef5350}{◀先頭~第100項まで37項}\\
&\small \displaystyle = 1369\\
\end{split}
と求めることができたので、
\begin{split}
&\small \displaystyle \frac{1+3+5+\cdots + 73}{2^7}=\color{#ef5350}{\frac{1369}{128}\space \cdots ②}
\end{split}
①、②より、群単位の和と端数部分の和を足した合計が初項~第100項までの和になるので
\begin{split}
\small \displaystyle \frac{63}{2}+\frac{1369}{128} &\small=\frac{4032+1369}{128}\\
&\small=\color{red}{\frac{5401}{128} \space \cdots 【答】}\\
\end{split}
【問題3】値が第何項目かの求め方
\(\small 2\)の累乗を分母とする既約分数を次のように並べた数列
$$\small \displaystyle \frac{1}{2}, \frac{1}{4},\frac{3}{4},\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8},\frac{1}{16},\frac{3}{16},\frac{5}{16},\cdots,\frac{15}{16},\frac{1}{32},\cdots$$
について、\(\small \displaystyle \frac{101}{256}\)は第何項目か求めよ。
・STEP1:第何群の何番目かを把握する
・STEP2:『群単位の項数』+『端数部分の項数』に分けて第何項目かを求める
の2ステップで考えるのが定石。
【補足】
問題2は数列の総和を求める問題だったので、『数列の値』を群単位の和と端数部分の和に分けて考えたけど、問題3は先頭からの項数の総和を求める問題なので、『数列の項数』を群単位の和と端数部分の和に分けて考えるってことだね。
まずは\(\small \displaystyle \frac{101}{256}\)が第何群に属するかを求めます。これは簡単で、分母が\(\small 2^n\)のかたまりが第\(\small n\)群にになるので、今回は\(\small 256=2^8\)であることから、第8群に属しています。
次に第8群の何番目に位置するかを考えます。これは、分子の奇数列の第\(\small k\)項目(\(\small k\)番目)が\(\small a_k=2k-1\)であることを考えると、\(\small a_k=101\)となる\(\small k\)の値を求めれば何番目に位置するかが分かります。
よって、
\begin{split}
&\small 2k-1 =101\\
\small \Leftrightarrow \space &\small 2k=102\\
\small ∴ \space &\small k=51\\
\end{split}
ゆえに、51番目と求まりました。
まとめると、\(\small \displaystyle \frac{101}{256}\)は第8群の51番目に位置することが分かりました。この状況を図にすると以下のようになります。
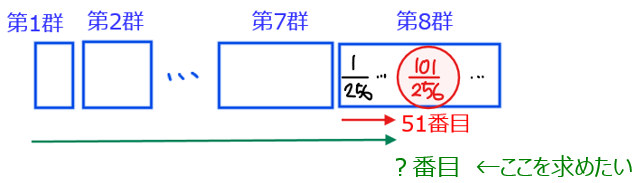
【ここに注意!】
51番目というのはあくまで\(\small \displaystyle \frac{101}{256}\)が第8群目の先頭から51番目に位置している(上図の赤字)という意味であって、今回問題で問われているのは数列の先頭から何番目か(上図の緑字)である点に注意しよう。
先頭から何番目の項であるかは、「第1群~第7群までの合計項数(項数の和)」と「第8群の先頭~51番目までの項数」の合計を出せば求めることができます。
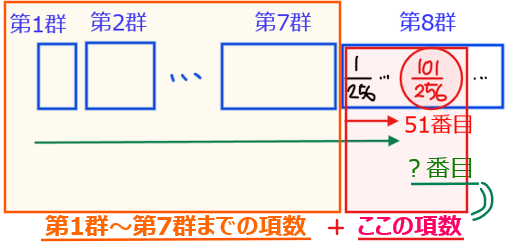
「第8群の先頭~51番目までの項数」のこと。
ただし、2つ目の第8群の先頭から51番目までの項数は明らかに51個…① とすぐ分かるので、1つ目の第1群~第7群までの合計項数を考えることができればOKです。
●第1群~第7群までの合計項数(項数の和)
第\(\small k\)群の項数は\(\small 2^{k-1}\)個(問題1の③より)だったので、
\begin{split}
\small \sum_{k=1}^7 2^{k-1} &\small = \frac{2^7-1}{2-1} \space ◀初項1、公比2の等比数列の和\\
&\small =\color{#ef5350}{127 \space \cdots ②}
\end{split}
①、②より、\(\small \displaystyle \frac{101}{256}\)の先頭からの項数は、①+②より、\(\small 51+127=178\)と求めるので、第178項目…【答】.
【問題4】第n項目の値の求め方
\(\small 2\)の累乗を分母とする既約分数を次のように並べた数列
$$\small \displaystyle \frac{1}{2}, \frac{1}{4},\frac{3}{4},\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8},\frac{1}{16},\frac{3}{16},\frac{5}{16},\cdots,\frac{15}{16},\frac{1}{32},\cdots$$
について、第\(\small 2025\)項目の値を求めよ。
・STEP2:群の規則性から値を求める
【補足】
解き方としては問題2とほぼ同じです。問題2は初項から第100項目までの和を求める問題で、和を求めるにあたって第100項目が第何群の何番目に位置するかを求めています。今回はそこから群数列の規則性をもとに具体的な項の値を答えれば解答になります。
初項から第\(\small n\)群までの合計項数は問題2の結果より、\(\small 2^n-1\)個(求め方は問題2を確認してね)。あとは第2025項目が含まれるような\(\small n\)の値を特定していきます。
\(\small 2^{10}=1024\)(これはよく使うので覚えておくとよい)、\(\small 2^{11}=2048\)であることから、第2025項目は第\(\small 11\)群に含まれることが分かります [*1]。
*1:補足
厳密には第\(\small n\)群までの合計項数は\(\small 2^n-1\)なので、\(\small 2^{10}-1\)と\(\small 2^{11}-1\)の値を2025と比較すべきですが、誤差なので\(\small 2^n\)で比較しちゃってます。解答にはこの過程は書かずに「n群までの項数が\(\small 2^n-1\)であることから第2025項目は第11群に含まれる」などと結果だけ記載すればよいでしょう。
第10群までの項数合計は、\(\small 2^n-1\)に\(\small n=10\)を代入することで、\(\small 2^{10}-1=1023\)個と求まるので、第11群には\(\small 2025-1023=1002\)個の項が存在することになります。よって、第2025項目は、第11群の1002番目に位置する項であることが分かります。
あとは本問の群の規則性から、第\(\small n\)群の分母は\(\small 2^n\)、群の先頭から\(\small k\)番目の分子の値は\(\small 2k-1\)であることから、2025項目は\(\small n=11\)、\(\small k=1002\)になるので、
$$\small \displaystyle \frac{2\cdot 1002 -1}{2^{11}}=\color{red}{\frac{2003}{2048}\space \cdots 【答】}$$
本記事のまとめ
今回は、分数の群数列における 総和の求め方・第何群かの判定・何番目の項かの求め方 をパターン別に分かりやすく解説しました。群数列は、一般的な数列のように公式へ代入すればすぐ解けるわけではなく、群ごとの規則性の把握やまとまり(群)単位で項数や和を整理して考えることが重要となります。この手順の複雑さがつまずきやすい理由でもあり、苦手意識が生まれやすいポイントと言えます。
解き方を整理する際に最も効果的なのは、解説の中でも出てきたような 図や表で数列の情報を可視化することです。数学の問題は、数式だけを使って考える必要はありません。群数列の構造を図表に落とし込むことで、思考が整理され、群数列の仕組みが驚くほど簡単に理解できるようになるので、図表をかいてない人は一度騙されたと思ってかいて解いてみることをおすすめします!
でもどんな図表を描けばいいのかはじめは難しいと思います。そこで、さらに詳しい整理術として、表を活用した裏ワザ的解法を別記事「第n群の総和と「何群・何番目」の求め方を徹底解説|表を活用した群数列の裏ワザ的解法」で解説しています。特に「頭の中がぐちゃぐちゃになる…」「数式の規則性が追えない」というタイプの方に効果的なので、併せて確認すると理解が一段階深まります。
今回は以上です。お疲れさまでした!







コメント