今回は平行移動や周期が変化した三角関数のグラフの書き方について解説します。三角関数のグラフの問題は、『\(\small \displaystyle y=2\sin\left(2x+\frac{\pi}{3}\right)+1\)のグラフの概形と周期を求めよ』といった問題のように、いろいろなところに数字が出てくるので一気に考えると混乱しがちです。
本記事では、問題パターンごとにそれぞれの数字の意味とグラフの概形がどう変わっていくのかの解説と、グラフを書く上で必要となる周期や\(\small x,y\)軸との交点の座標などの求め方のコツを分かりやすく解説していこうと思います。
- 平行移動・周期が変化した三角関数のグラフの書き方について知りたい
- グラフを書くときは、軸との交点などを何をどこまで書けばいいのか知りたい
- 三角関数のグラフの書き方を問題パターン別に理解したい
【基礎講義】三角関数のグラフの書き方とコツ
【講義1】三角関数の一般形
三角関数はこれまで学んだ1次関数や2次関数などとは異なり、いろいろな部分に数字が出てくることが問題を難しくしている大きな原因になっていると思います。
そこで、まずはじめに三角関数の一般形とそれぞれの数字の意味から確認しておきましょう。これが理解できれば、あとは三角関数のグラフを書く様々な問題パターンのすべてに対応できるようになります!
ちょっと複雑に見えますが、現時点で理解しておいてほしい点は、「\(\small y=\sin x\)という基本形が平行移動とか周期変更されることで、一般的には上記のような式になる」ということです。ポイントは、\(\small y=\sin x\)の基本形が出発点になるという点です。
なお、三角関数は、\(\small \sin, \space ,\cos \space ,\tan\)の3種類がありますが、考え方自体はどれも同じなので、ここでは\(\small \sin\)の場合を代表例として解説していきます。
次の講義で具体的に\(\small y=\sin x\)のグラフをどのように変形して一般形になっていくのかについて順番に解説していきます。
【講義2】パターン①(\(\small y=\sin x\))【基本形】
復習として、三角関数の基本形 \(\small y=\sin x\)のグラフと特徴は以下の通りでした。
●\(\small y=\sin x\)のグラフの概形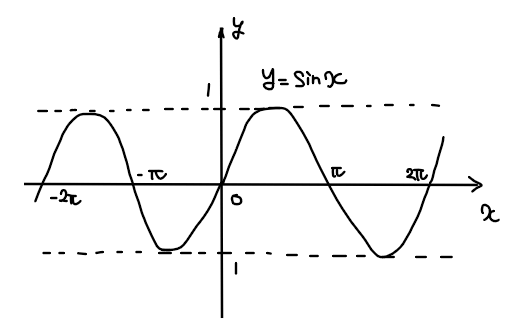
●\(\small y=\sin x\)のグラフの特徴
・\(\small y\)の範囲:\(\small -1≦y≦1\)
・周期:\(\small 2\pi\)
☞ グラフは\(\small 0≦x <2\pi\)の形を繰り返す
・対称性:原点対称
☞ 原点を中心として\(\small 180°\)回転してもグラフの概形が一緒
まずは、この基本形のグラフの概形をしっかり押さえましょう。
【講義3】パターン②(\(\small y=A\sin x\))【振幅】
では、ここからは基本形を少し変化させた\(\small y=\mathrm{A}\sin x\)のグラフの概形について考えていきましょう。基本形は\(\small \mathrm{A}=1\)という特殊な場合だったと考えることができます。
\(\small y=\mathrm{A}\sin x\)のグラフの概形は、下図の赤線ような概形になります。
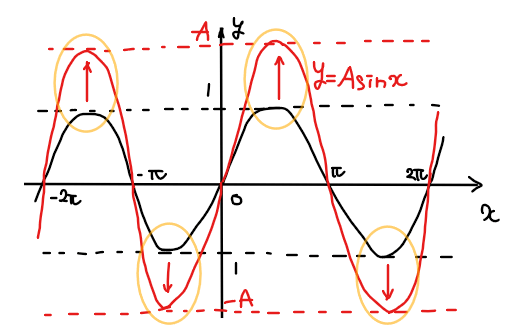
ポイントは、\(\small y\)方向の振れ幅が\(\small -1≦y≦1\)から\(\small -\mathrm{A}≦y≦\mathrm{A}\)に変わっていること。
ではなぜこのような概形になるか?それは、\(\small y=\mathrm{A}\sin x\)の\(\small y\)の取り得る値の範囲を考えると
\begin{split}
&\small -1 ≦\sin x≦1\\
\small \Leftrightarrow \space &\small \color{#ff4281}{-\mathrm{A} }≦ \mathrm{A}\sin x≦\color{#ff4281}{\mathrm{A}} \quad [*1]\\
\small \Leftrightarrow \space &\small \color{#ff4281}{-\mathrm{A} }≦ y≦\color{#ff4281}{\mathrm{A}} \quad ◀ y=\mathrm{A}\sin x\\
\end{split}
となるからです。
*1:【補足】式変形について
\(\small \mathrm{A}<0\)の場合は不等号の向きが変わるので厳密には場合分けが必要ですが、今回は不等式の上限と下限が符号反転であることから、結果的に同じ結論になるので省略してます。気になる人は\(\small \mathrm{A}<0\)を両辺にかけ算するときに不等号の向きが変わることに注意して実際に計算してみると結果が同じになることが分かると思います。
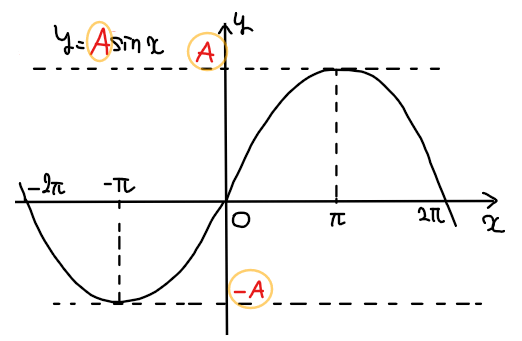
≫グラフの特徴
・\(\small y\)の範囲:\(\small -\mathrm{A}≦y≦\mathrm{A}\)
・周期:\(\small 2\pi\)
・対称性:原点対称
【講義4】パターン③(\(\small y=\sin kx\))【周期】
今度は基本形\(\small y=\sin x\)の\(\small x\)を\(\small k\)倍した式 \(\small y=\sin kx\)のグラフの概形について考えてみます。
三角関数の基本形では関数の周期は\(\small 2\pi\)が周期でしたが、これは\(\small \sin x\)の角度が \(\small 0≦x≦2\pi\)で単位円を一周するからでした。
三角関数の周期は、単位円の一周分と考えることがポイントです!
一周は\(\small 360°=2\pi\)なので、\(\small \sin \theta\) が単位円上を一周するときの角度 \(\small \theta\)の範囲は、\(\small 0≦\theta <2\pi\)となります。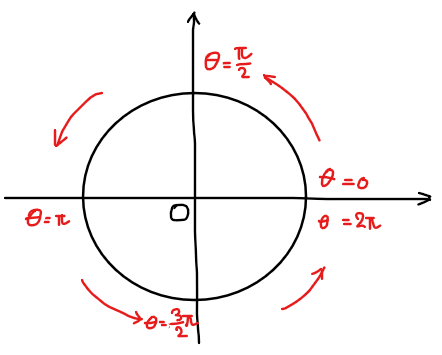
今回のように変数が\(\small k\)倍されたときの三角関数の周期を考えたければ、角度を\(\small \theta = kx\)と見なしてあげればOKで、\(\small kx\)が単位円を一周する範囲は\(\small 0≦ kx ≦2\pi\)で求めることができるので、
\begin{split}
&\small \displaystyle 0≦ kx ≦2\pi\\
&\small \displaystyle 0≦ x ≦\frac{2\pi}{k} \quad ◀xはこの範囲で単位円を一周\\
\end{split}
となります。故に、関数の周期は\(\small \displaystyle \frac{2\pi}{k}\)になります(\(\small 0~2\pi/k\)で単位円を一周するので)。
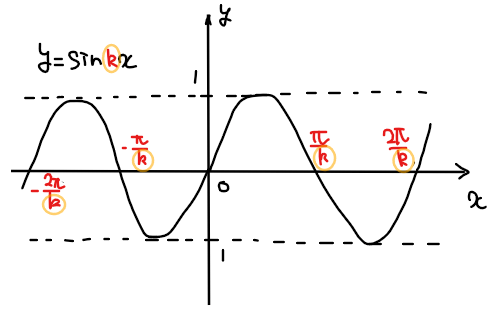
≫グラフの特徴
・\(\small y\)の範囲:\(\small -1≦y≦1\)
・周期:\(\small \displaystyle \frac{2\pi}{k}\)
・対称性:原点対称
【講義5】パターン④(\(\small y=\sin (x-\alpha)+\beta\))【平行移動】
最後は平行移動です。これは、三角関数特有の考え方というよりは、他の関数にも一般的に成り立つ考え方です。
平行移動とは、グラフの向きや形が変わらないような縦方向や横方向へのグラフ移動という意味です。斜め方向の移動は考えないの?と思った人もいるかもしれないですが、斜め方向への移動は結局は縦移動と横移動の組み合わせなので縦横方向の移動だけを考えればOKです!
逆に、向きや形が変わるような引き延ばしや反転、回転は平行移動とは言いません。
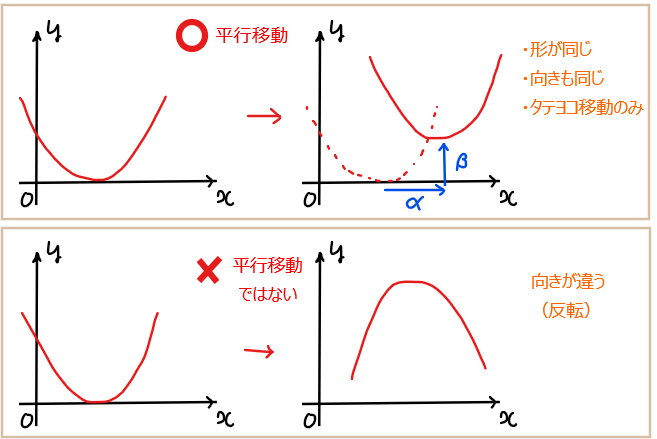
平行移動した関数の式は以下のように簡単に求めることができます。
この考え方を用いると三角関数の基本形 \(\small y=\sin x\)を\(\small x\)軸方向に\(\small \alpha\)、\(\small y\)軸方向に\(\small \beta\)だけ平行移動した三角関数の式は、
\begin{split}
&\small y = \sin x\\
\small ⇒ \space &\small y \color{#ef5350}{- \beta} = \sin (x\color{#ef5350}{-\alpha})\\
&\small y = \sin (x-\alpha) + \beta\\
\end{split}
となります。
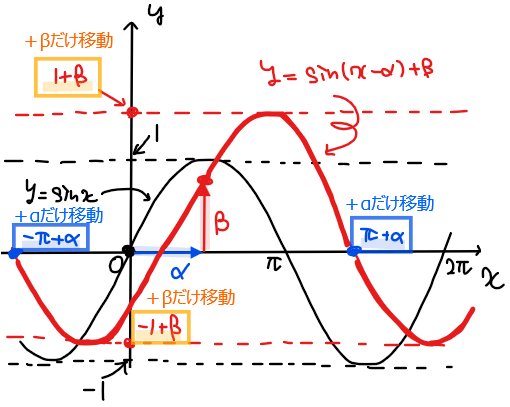
一見すると複雑そうに見えますが、\(\small x\)軸や\(\small y\)軸とグラフの交点は、基本形\(\small y=\sin x\)(黒線)の交点にそれぞれ平行移動した\(\small \alpha\)、\(\small \beta\)を加えるだけで求めることができます。
・ \(\small y\)の範囲: \(\small -1+\beta≦y≦1+\beta\)
・周期:\(\small 2\pi\)
・対称性:点\(\small (\alpha ,\beta)\)対称
【講義6】三角関数で押さえるべき4つの数字
講義2~5までの内容を組み合わせると、冒頭に触れた三角関数の一般形のグラフの概形は次のように説明できます。
は基本形\(\small y=\sin x\)のグラフを
【①】振幅を\(\small \mathrm{A}\)倍(\(\small y=\mathrm{A}\sin x\))し、
【②】周期を\(\small \displaystyle \frac{2\pi}{k}\)にした三角関数(\(\small y=\mathrm{A}\sin kx\))を、
【③】\(\small x\)軸方向に\(\small \alpha\)、
【④】\(\small y\)軸方向に\(\small \beta\)だけ平行移動(\(\small y-\beta=\mathrm{A}\sin k(x-\alpha)\))
した三角関数。
【補足】\(\small y=\mathrm{A}\sin kx\)の平行移動
\(\small y=\sin x\)を\(\small x\)軸方向に\(\small \alpha\)、\(\small y\)軸方向に\(\small \beta\)だけ平行移動した三角関数の式は、\(\small y=\mathrm{A}\sin (kx-\alpha)+\beta\)ではないことに注意!
平行移動の式はあくまで変数\(\small x\)の部分だけを\(\small x-\alpha\)に置き換えるので\(\small kx\)は\(\small k(x-\alpha)\)に置き換える必要があります。
三角関数のグラフでは、三角関数の振動の振れ幅を決める振幅\(\small \mathrm{A}\)、関数の周期を決める\(\small k\)、平行移動を表す\(\small \alpha, \beta\)という4つの数字に着目して確認していくことで、グラフの概形がとても書きやすくなると思います。
では実際の問題を通してグラフの書き方を確認していきましょう。
【パターン別】三角関数のグラフ問題
【基礎確認】三角関数の概形情報の読み取り
以下の三角関数は、[]内の三角関数をどのように変形した関数になっているか答えよ。また、関数の周期を求めよ。
(1)\(\small \displaystyle y=\frac{1}{3}\sin x \quad [y=\sin x]\)
(2)\(\small y=4\sin x-1 \quad [y=\sin x]\)
(3)\(\small \displaystyle y=2\cos\left(3x-\frac{\pi}{2}\right)+3 \quad [y=\cos 3x]\)
三角関数の一般形と比較すると \(\small \displaystyle \mathrm{A}=\frac{1}{3}\)であることから、\(\small y=\sin x\)のグラフを\(\small y\)軸方向に\(\small \displaystyle \frac{1}{3}\)倍…【答】したグラフになります。
周期は\(\small \sin x\)の\(\small x\)の係数に変わりがない(\(\small k=1\))ことから、\(\small y=\sin x\)と同じく\(\small 2\pi\)…【答】となります。
三角関数の一般形と比較すると \(\small \displaystyle \mathrm{A}=4\), \(\small \beta =-1\)であることから、\(\small y=\sin x\)のグラフを\(\small y\)軸方向に\(\small 4\)倍し、\(\small y\)軸方向に\(\small -1\)だけ平行移動…【答】したグラフになります。
周期は\(\small k=1\)なので、\(\small 2\pi\)…【答】となります。
三角関数の一般形 \(\small y=\mathrm{A}\sin k(x-\alpha)+\beta\)になるように式変形すると
\begin{split}
\small \displaystyle y &\small =2\cos\left(3x-\frac{\pi}{2}\right)+3\\
&\small =2\cos 3\left( x-\frac{\pi}{6}\right)+3\\
\end{split}
よって、\(\small \displaystyle \mathrm{A}=2\), \(\small k=3\), \(\small \displaystyle \alpha =\frac{\pi}{6}\), \(\small \beta =3\)であることから、\(\small y=\cos 3x\)のグラフを\(\small y\)軸方向に\(\small 2\)倍し、\(\small x\)軸方向に\(\small \displaystyle \frac{\pi}{6}\)、\(\small y\)軸方向に\(\small 3\)だけ平行移動…【答】したグラフになります。
\(\small \displaystyle \cos\left(3x-\frac{\pi}{2}\right)\)の形だけみて、\(\small x\)軸の平行移動が\(\small \displaystyle \frac{\pi}{2}\)と判断しないように注意。
周期は\(\small k=3\)なので、
\begin{split}
\small \displaystyle \frac{2\pi}{k} &\small =\color{red}{\frac{2\pi}{3} \space \cdots 【答】}\\
\end{split}
となります。
【基本問題1】三角関数の振幅
\(\small y=3\sin x\)のグラフをかけ。
問題の三角関数が\(\small \sin x\)に関する関数なので、基本形\(\small y=\sin x\)からの変化を考えていきます。
【講義6】三角関数で押さえるべき4つの数字の\(\small \mathrm{A}=3\)のパターンなので、問題の三角関数は、\(\small y=\sin x\)を\(\small y\)軸方向に3倍に拡大したグラフになります(振幅が\(\small -3≦y≦3\)に変化)。
関数の周期は\(\small k=1\)より変わらず\(\small 2\pi\)なので、グラフの概形は以下のようになります。
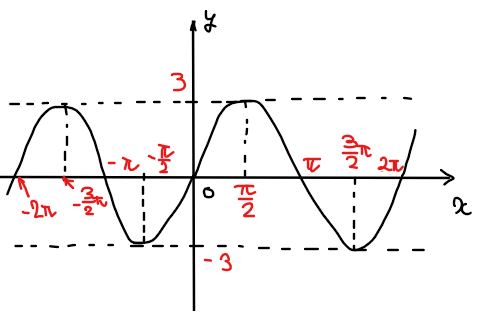
【基本問題2】三角関数の周期
\(\small \displaystyle y=\sin \frac{3}{2}x\)のグラフをかけ。
☞ 変数\(\small x\)の係数 \(\small k\)に着目
\(\small \displaystyle k = \frac{3}{2}\)であることから、問題の三角関数の周期は
\begin{split}
\small \frac{2\pi}{\color{#ef5350}k} &\small \displaystyle = \frac{2\pi}{\color{#ef5350}{\dfrac{3}{2}}}\\
&\small= \frac{4\pi}{3} \\
\end{split}
周期以外は基本形 \(\small y=\sin x\)のグラフから変わらないので、グラフの概形は以下のようになる。
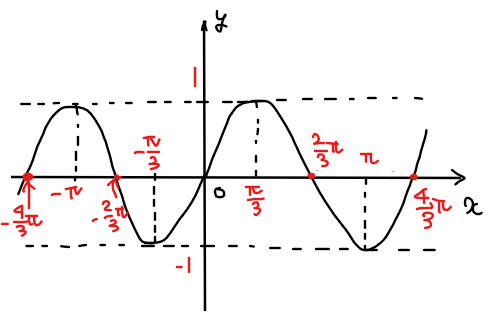
【補足】軸との交点の求め方
グラフの\(\small x\)軸との交点は周期の半分である\(\small \displaystyle \frac{2\pi}{3}\)、山はさらに半分の\(\small \displaystyle \frac{\pi}{3}\)、谷は周期の\(\small \displaystyle \frac{3}{4}\)倍の位置なので、\(\small \displaystyle \frac{4\pi}{3} \times \frac{3}{4}=\pi\)のように求めることができる。
一般に、周期が\(\small a\pi\)の場合、山は\(\small \displaystyle \frac{a\pi}{4}\)、\(\small x\)軸との交点は\(\small \displaystyle \frac{a\pi}{2}\)、谷は\(\small \displaystyle \frac{3a\pi}{4}\)となる。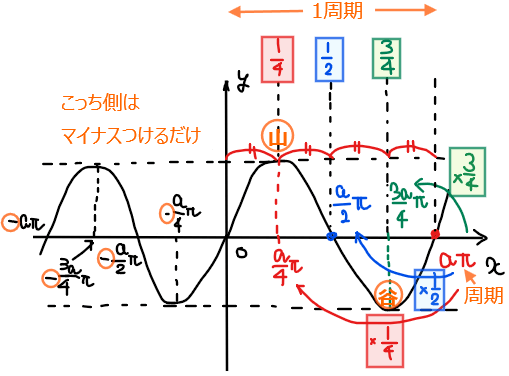
【基本問題3】三角関数の平行移動
\(\small \displaystyle y=\sin \left(x+\frac{\pi}{2}\right)+1\)のグラフをかけ。
詳細は、【講義5】パターン④(\(\small y=\sin (x-\alpha)+\beta\))【平行移動】を参照。
問題のグラフは三角関数 \(\small y=\sin x\)を\(\small x\)軸方向に\(\small \displaystyle -\frac{\pi}{2}\)、\(\small y\)軸方向に\(\small 1\)だけ平行移動したグラフになるので、グラフのスタート地点が原点から、\(\small \displaystyle \color{red}{\left(-\frac{\pi}{2},1\right)}\)になります。
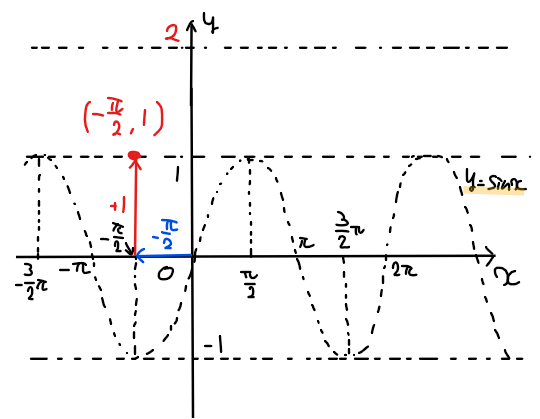
あとは\(\small y=\sin x\)のグラフをそのままスライドしてくればグラフの概形の完成です。
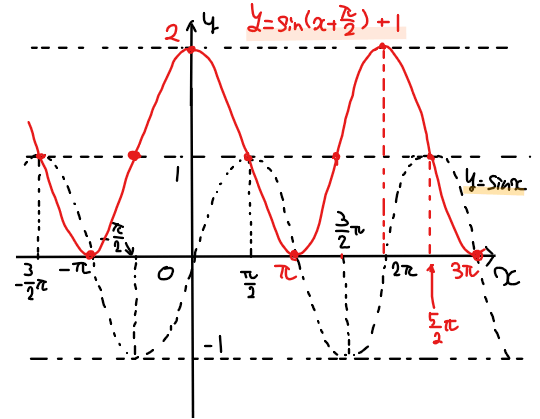
【補足】平行移動後のグラフを書くコツ
平行移動させるときにどの点を通るのか考えるのが苦手という人は多いと思います。イメージが湧きにくいという人は、\(\small y\)軸方向に移動をしてから\(\small x\)軸方向に移動するという2段階に分けて移動を考えるようにしましょう。移動の順番は\(\small x\)軸方向に移動した後に\(\small y\)軸方向に移動でもOKです。
たとえば、本問を\(\small y\)軸方向→\(\small x\)軸方向の順で考えると、\(\small y\)軸方向は\(\small \beta=1\)より1だけ全体を上側に移動させればよいので、下図の赤線のようなグラフになります。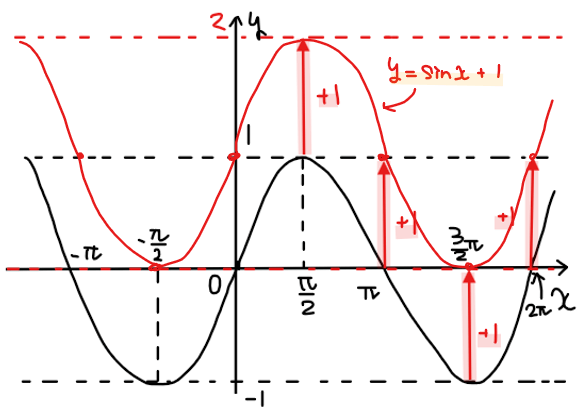
次に、この赤線のグラフを\(\small x\)軸方向に\(\small \displaystyle -\frac{\pi}{2}\)だけ移動させます(左側に\(\small \displaystyle \frac{\pi}{2}\)ずらす)。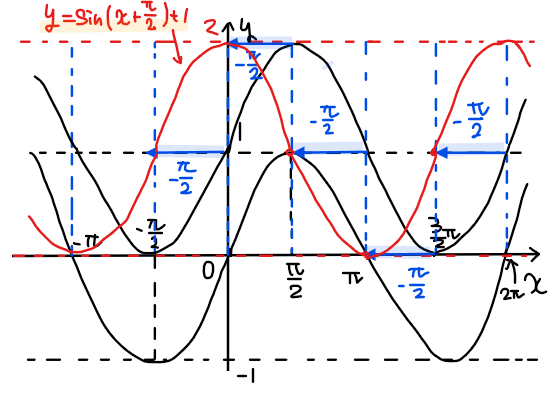
このように2段階で考えることで求めたかった\(\small xy\)方向に平行移動した関数のグラフを求めることができます。
【実践問題】三角関数の一般形
\(\small \displaystyle y=2\sin \left(2x+\frac{\pi}{3}\right)+1\)のグラフをかけ。また、その周期を求めよ。
・\(\small y=\mathrm{A}\sin kx\)を平行移動した関数と考えるとグラフを書きやすい。
・グラフの図示問題では、山(最大値)、谷(最小値)、\(\small x\)軸、\(\small y\)軸との交点を明記しよう。
問題の三角関数を一般形に式変形すると
\begin{split}
\small y &\small \displaystyle =2\sin \left(2x+\frac{\pi}{3}\right)+1\\
&\small \displaystyle =2\sin \color{#ef5350}2\left(x+ \color{#ef5350}{\frac{\pi}{6}}\right)+1\\
\end{split}
となることから、\(\small \mathrm{A}=2,\) \(\small k=2,\) \(\small \displaystyle \alpha=-\frac{\pi}{6},\) \(\small \beta=1\)であることが分かります [*1]。
*1:【補足】平行移動\(\small \alpha \)を求める注意点
問題の式を見て\(\small x\)軸方向の平行移動を\(\small \displaystyle \color{red}{-\frac{\pi}{3}}\)としてしまうミスに注意しましょう。
このような凡ミスを回避するためにも、頭の中で計算するのではなく、角度部分は必ず\(\small \displaystyle k(x-\alpha)\)の形になるように式変形するとミスが減ります。
また、式変形に気をとられて符号を逆転させるのを忘れるミスも多いので気を付けましょう!
求めた4つの数字から分かることを整理すると、『①:振幅が\(\small 2\)、周期が\(\small \displaystyle \frac{2\pi}{k}=\pi\)である\(\small y=2\sin 2x\)のグラフ』を『②:\(\small x\)軸方向に\(\small \displaystyle -\frac{\pi}{6}\)、\(\small y\)軸方向に\(\small 1\)だけ平行移動した三角関数』を書けばよいことが分かります。
答えの一部である関数の周期については\(\small \pi\)…【答】であることがこの時点で求まりました。
ではグラフの図示に話を戻して、いきなり求める関数のグラフを書こうとすると難しいので、まずは上記の①の関数を書いてから、②の平行移動をして求める関数を書くという2段階でグラフを書いていきましょう。
ではまずは①:\(\small y=2\sin 2x\)のグラフを書くと下図のようになります。
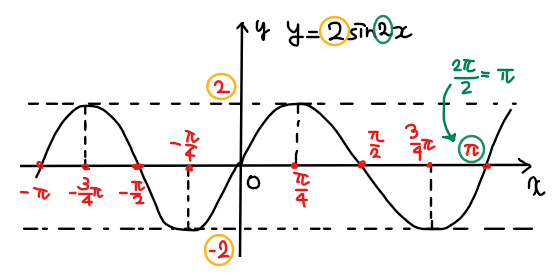
振幅が\(\small 2\)、周期が\(\small \pi\)のサインカーブを書けばよい。
次に、今書いた①のグラフに対して②の平行移動(\(\small x\)軸方向に\(\small \displaystyle -\frac{\pi}{6}\)、\(\small y\)軸方向に\(\small 1\))を行います。
\(\small y\)軸方向の平行移動は簡単で、全体を\(\small 1\)だけ上方向に持ち上げればよいので、もともと\(\small -2≦y≦2\)の範囲で波打っていた関数が、\(\small -1≦y≦3\)の範囲に変化します。このラインをまずは書いてあげます。
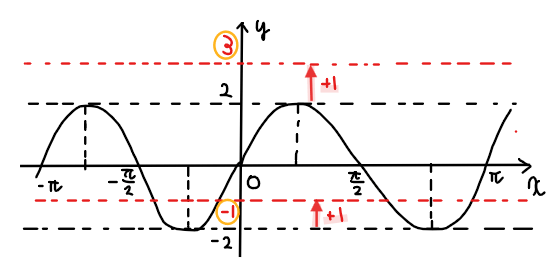
\(\small x\)軸方向の平行移動については、全体を負の向き(左方向)に\(\small \displaystyle \frac{\pi}{6}\)移動させればよいので、①のグラフの山、\(\small x\)軸との交点、谷の座標をそれぞれ\(\small \displaystyle -\frac{\pi}{6}\)した座標をプロットします。
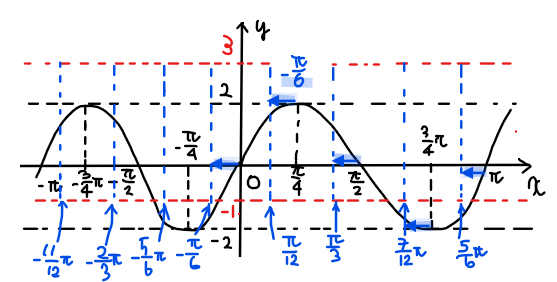
あとは、平行移動によって、グラフのスタート地点がもともと原点だったのが、\(\small \displaystyle \left(-\frac{\pi}{6},1\right)\)に移動していることに注意すれば下図のようなグラフの概形になることが分かります。
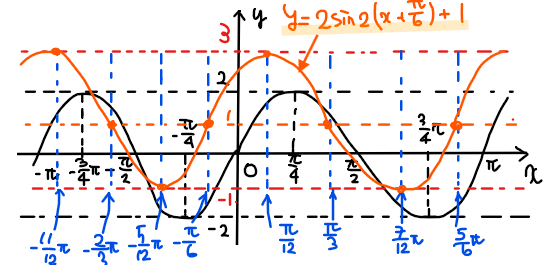
最後に、グラフを書く問題ではグラフと各軸との交点くらいは求めておいた方がよいので、\(\small x\)軸、\(\small y\)軸との交点を求めて図に記入すればおしまいです。
<\(\small x\)軸との交点の求め方>
\(\small x\)軸上では\(\small y=0\)なので、
\begin{split}
&\small 0 =2\sin 2\left(x+ \frac{\pi}{6}\right)+1\\
\small \Leftrightarrow \space &\small \sin 2\left(x+ \frac{\pi}{6}\right)=-\frac{1}{2}\\
\small ∴ \space &\small 2\left(x+ \frac{\pi}{6}\right) = \frac{7}{6}\pi+2n\pi, \space \frac{11}{6}\pi+2n\pi \quad [*2]
\end{split}
(ただし、\(\small n\)は整数)。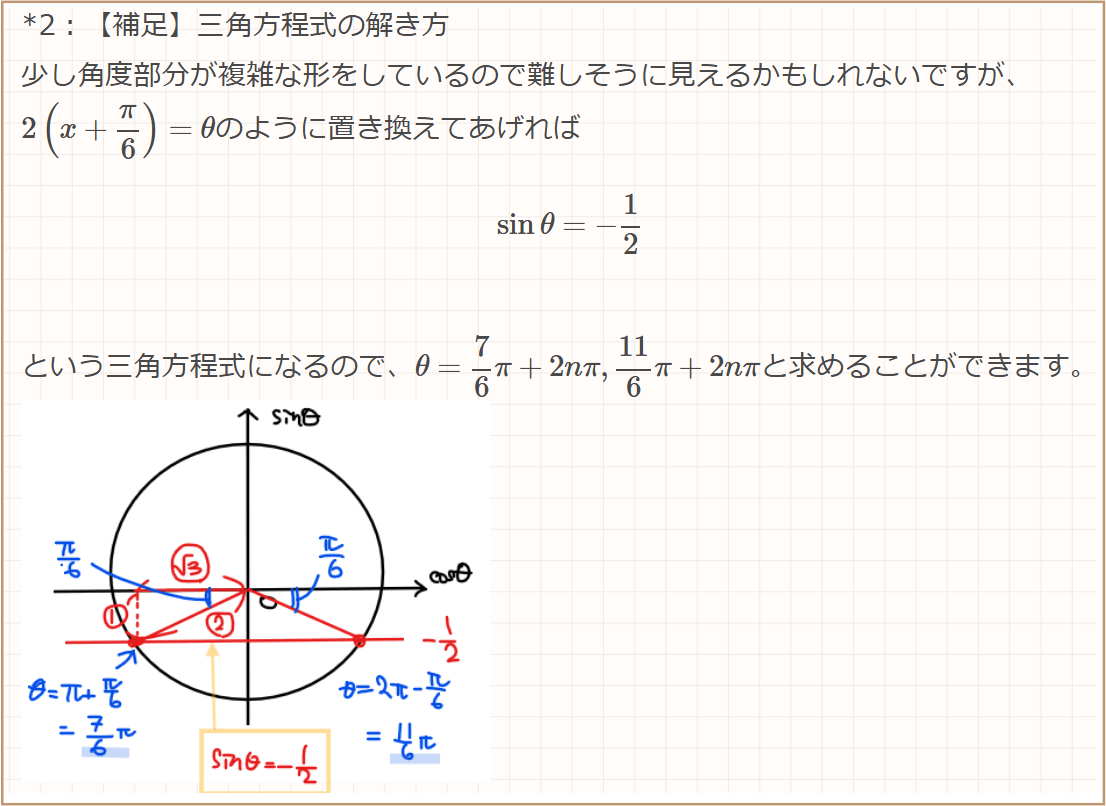
それぞれの方程式を解いて\(\small x\)の値を求めると
\begin{split}
&\small 2\left(x+ \frac{\pi}{6}\right) = \frac{7}{6}\pi+2n\pi\\
&\small x+ \frac{\pi}{6}= \frac{7}{12}\pi+n\pi\\
&\small x= \frac{5}{12}\pi+n\pi \space \cdots ①\\
\end{split}
\begin{split}
&\small 2\left(x+ \frac{\pi}{6}\right) = \frac{11}{6}\pi+2n\pi\\
&\small x+ \frac{\pi}{6}= \frac{11}{12}\pi+n\pi\\
&\small x= \frac{3}{4}\pi+n\pi \space \cdots ②\\
\end{split}
(ただし、\(\small n\)は整数)。
よって、グラフと\(\small x\)軸との交点は、原点に近い順に、\(\small n=0, \pm1,\cdots\)と代入していけばよい(基本的には\(\small n=0,\pm1\)くらいまで求めれば十分だと思います)ので、①は、\(\small n=-1,0,1\)の順に
\begin{split}
&\small -\frac{7}{12}\pi, \space \frac{5}{12}\pi, \space \frac{17}{12}\pi
\end{split}
②も\(\small n=-1,0,1\)の順に
\begin{split}
&\small -\frac{\pi}{4}, \space \frac{3}{4}\pi, \space \frac{7}{4}\pi
\end{split}
①、②の結果を合わせると
\begin{split}
&\small -\frac{7}{12}\pi, \space -\frac{\pi}{4},\space \space \frac{5}{12}\pi, \space \frac{3}{4}\pi, \frac{17}{12}\pi, \space \frac{7}{4}\pi
\end{split}
となることが分かります。
<\(\small y\)軸との交点の求め方>
\(\small y\)軸上では\(\small x=0\)なので、
\begin{split}
\small y &\small =2\sin 2\left(0+ \frac{\pi}{6}\right)+1\\
&\small =2\sin \frac{\pi}{3}+1\\
&\small =2\cdot \frac{\sqrt{3}}{2}+1\\
&\small =\color{#ef5350}{\sqrt{3}+1}\\
\end{split}
以上より、最終的なグラフの概形は、不要な線を消して軸との交点を書き足した下図のような図示ができればよいでしょう…【答】.
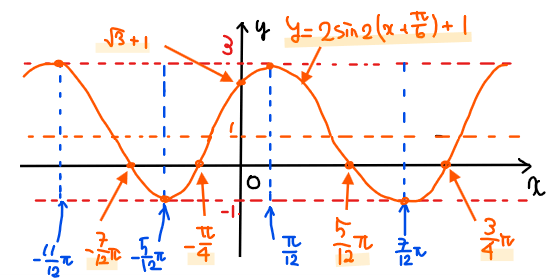
本記事のまとめ
今回は三角関数のグラフの書き方について解説してみました。共通テストや大学入試では実際にグラフを書く問題というよりは、グラフを読み取ったり、式から概形をイメージできる力が問われることになるので、今回紹介した一般形と4つの数字の図形的な意味合いをしっかり押さえておきましょう。
また、今回紹介したのは\(\small \sin x\)関数のグラフの概形でしたが、他にも\(\small \cos x\)や\(\small \tan x\)のグラフもあります。\(\small \cos x\)は形が少し異なるだけで周期や平行移動の考え方自体は同じなので、今回紹介した解法をもとに実際に問題を解いてみましょう。
\(\small \tan x\)のグラフはサインやコサイン関数とは少し概形が異なるので、別記事で解説しようかなと思っています。
では今回は以上です。お疲れさまでした!








コメント