【三角方程式】方程式の解の個数・解の存在条件の求め方（三角方程式の応用問題を徹底解説）

今回は三角方程式の解の個数や解の存在条件を求める問題について徹底解説していきます。この分野は三角関数の知識に加えて2次方程式の解の存在範囲に関する知識も求められることから、大学入試や定期テストの応用問題として頻出の分野になっています。

解き方を暗記して解く問題というよりは、解答に至るまでの思考プロセスが重要になってくるので、本記事でも解答を導くまでの考え方に重点を置いて、詳しく解説していこうと思います！

それでは、早速確認していきましょう！

　本記事はこんな人におすすめ

三角方程式の解の個数、解の存在条件の問題の解き方を理解したい人
解の個数や解の存在条件の問題の解き方のコツ（重要な考え方）について知りたい人
定期テスト対策、大学受験対策がしたい人

　本記事のレベル

重要度

低

余力あれば

普通

必須

高
難易度

易しい

易

やや易

やや難

難

難しい
暗記/理解

暗記重視

暗記

半々

理解

理解重視

【問題＆解説】三角方程式の解の個数・解の存在条件
本記事のまとめ

【問題＆解説】三角方程式の解の個数・解の存在条件

【問題1】三角方程式の解の個数を求める問題（難易度：★★☆）

$\small a$を定数とする。$\small \theta $に関する方程式 $\small \sin^2 \theta -\cos\theta +a=0$について、次の問いに答えよ。ただし、$\small 0≦\theta < 2\pi$とする。
（1）この方程式が解を持つための$\small a$の条件を求めよ。
（2）この方程式の解の個数を$\small a$の値の範囲によって調べよ。

問題解決のKey

・2次方程式の解の配置問題として考える解法が基本線（問題2で解説）であるが、『三角関数を含む関数』＝『定数』の形に定数分離できる場合は、グラフから定数関数との共有点の個数を求める解法が簡単。

　解説（1）

問題の方程式は、$\small -\sin^2 \theta +\cos\theta =a$のように定数分離できる。

ここで、

\begin{split}
\small (左辺) &\small = -\color{#ef5350}{(1-\cos^2\theta)}+\cos\theta \quad \mathsf{\color{#ef5350}{◀文字種の統一}}\\
&\small = \cos^2\theta+\cos\theta-1\\
\end{split}

より、$\small \cos\theta =t$ とおくと、問題の方程式は

$$\small t^2+t-1=a \quad \cdots (*)$$

となり、$\small t$ に関する2次方程式とみなすことができる。ただし、$\small 0≦\theta<2\pi$の範囲では、$\small -1≦\cos\theta≦1$なので、$\small -1≦t≦1$…①であることに注意する。

$\small (*)$の方程式は、$\small -1≦t≦1$の範囲で、関数 $\small y=t^2+t-1$と定数関数$\small y=a$の共有点を求める方程式[*1]とみなせる。

*1：【補足】方程式の解釈
『$\small (*1)$が関数の共有点を求める方程式とみなせる』という部分がこの問題の最大のポイントであり、しっかりと理解してほしいポイントでもあるため考え方を補足する。
具体例で考えた方が分かりやすいと思うので突然だが以下の問題を見てほしい。

（問題）
関数 $\small y=x^2+2x+3$と関数 $\small y=x+1$の共有点の座標を求めよ。

この問題を解くとき、関数同士を
$$\small x^2+2x+3 = x+1$$
のように連立するだろう。左辺が関数 $\small y=x^2+2x+3$で、右辺が関数 $\small y=x+1$になっている。このことから、2つの関数の共有点の座標を求めたい場合は、2つの関数をイコールで結んだ方程式を解けばよいということになる。

この考え方を逆手に利用したものが今回の問題であり、方程式の左辺と右辺を『2つの関数をイコールで結んだもの』と解釈すると、左辺の関数と右辺の関数のグラフの共有点を求めるための方程式とみなすことができる。

すなわち、

『$\small (*)$の方程式が、解を持つ』　
⇔『$\small -1≦t≦1$の範囲で関数 $\small y=t^2+t-1$と定数関数$\small y=a$が、共有点を持つ』

という2次関数のグラフの問題に帰着させることができる。

\begin{split}
\small y &\small =t^2+t-1\\
&\small =\left(t+\frac{1}{2}\right)^2-\frac{5}{4}\\
\end{split}

より、2次関数 $\small y=t^2+t-1$は、軸が$\small \displaystyle t= -\frac{1}{2}$、頂点が$\small \displaystyle \left(-\frac{1}{2},-\frac{5}{4}\right)$のグラフなので、$\small -1≦t≦1$の範囲で定数関数 $\small y=a$と共有点を持つような $\small a$ 範囲は下図の紫色の範囲になる。

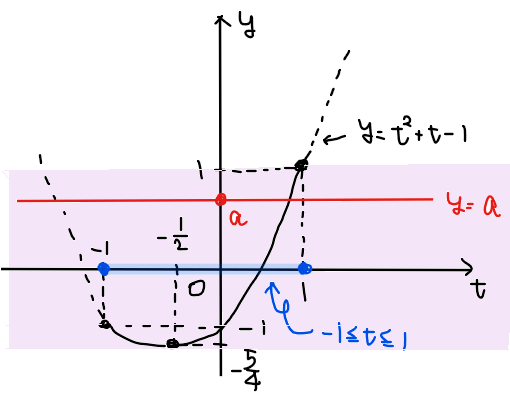
紫色の範囲が、関数 $\small y=t^2+t-1$（$\small -1≦t≦1$）（黒実線）と関数 $\small y =a$（赤実線）が交わる範囲

よって、求める範囲は図から$\small \displaystyle -\frac{5}{4}≦a≦1$…【答】.

　解説（2）

（1）のグラフを見ると2次関数と定数関数の交点の個数の関係は、

[1] $\small \displaystyle a<-\frac{5}{4}$、または $\small 1<a$のとき0個
[2] $\small \displaystyle a=-\frac{5}{4}$、または $\small -1<a≦1$のとき1個
[3] $\small \displaystyle -\frac{5}{4}<a≦-1$のとき2個

なので、「これが答え！」と言いたくなるが、これは『$\small t$の実数解の個数』であり、問題文で問われいているのは『$\small \theta $の解の個数』である点に注意されたい。つまり、$\small t$の解の個数と$\small \theta$の解の個数の関係性に着目する必要がある。

もともと、$\small t=\cos\theta$と設定していたので、$\small 0≦\theta <2\pi$の範囲では基本的には$\small \cos\theta $の値1個（$\small t$の値1個）に対して、対応する角度 $\small \theta $は2個存在する（たとえば、$\small \cos\theta = 1/2$であれば、$\small \theta =\pi/3,5\pi/3$の2個の解がある）。ただし、例外として$\small \cos\theta =\pm1$のときだけ$\small \theta $の値は1個（$\small t=1$のとき$\small \theta =0$、$\small t=-1$のとき$\small \theta =\pi$）である点に注意する。

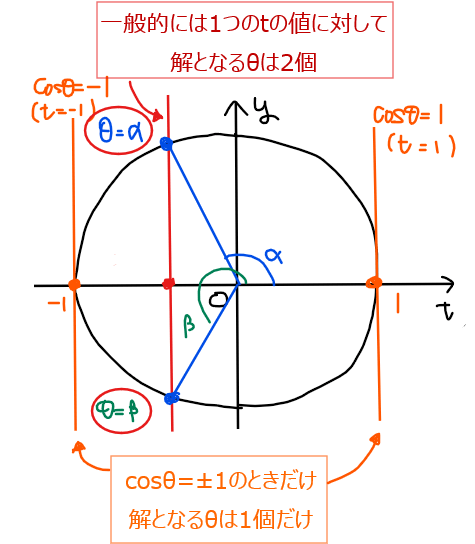
Point：$\small \sin\theta,\cos\theta$の値と解の個数の関係

・$\small -1<\cos\theta<1$のとき、$\small \theta$の解の個数は2個、
　$\small \cos\theta =\pm 1$のとき、$\small \theta$の解の個数は1個。
・$\small -1<\sin\theta<1$のとき、$\small \theta$の解の個数は2個、
　$\small \sin\theta =\pm 1$のとき、$\small \theta$の解の個数は1個

よって、$\small y=a$の位置ごとの$\small \theta$の解の個数は次のようになる[*2]。

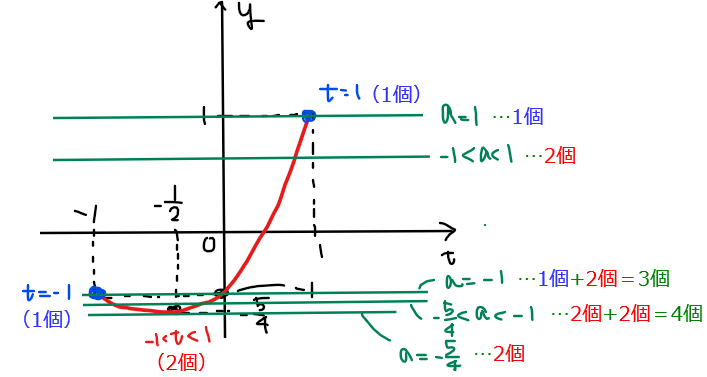
2次関数 $\small y=t^2+t-1$上で、青色箇所（$\small t= \pm1$）は解が1個、赤色箇所（$\small -1<t<1$）は解が2個であることから、定数関数（緑線）との共有点ごとに上図のような解の個数関係になる。

*2：【補足】解の個数のカウント方法
$\small a=1$であれば、青点のみ通過するので$\small \theta$の解の個数は1個、$\small -1<a<1$であれば、赤線部分のみと交わるので$\small \theta$の解の個数は2個、$\small a=-1$であれば、青点と赤線部分を1回ずつ交わるので$\small \theta$の解の個数は1+2=3個…という要領で解の個数をカウントすればよい。

ゆえに、解答は、

$\small \displaystyle a<-\frac{5}{4}$のとき0個、$\small \displaystyle a=-\frac{5}{4}$のとき2個、
$\small \displaystyle -\frac{5}{4}<a<-1$のとき4個、$\small a=-1$のとき3個、
$\small -1<a<1$のとき2個、$\small a=1$のとき1個、
$\small 1<a$のとき0個　　…【答】

【研究】解の配置問題に帰着させた解法

問題解決のKeyでも触れたが、（1）は2次方程式の解の配置問題に帰着させて解くこともできるので、参考として解法を紹介しておく。

[（1）の別解]
$\small \cos\theta =t$とおくと、問題文の方程式は
\begin{split}
&\small \sin^2\theta-\cos\theta+a=0\\
\small \Leftrightarrow \space &\small (1-t^2)-t+a=0\\
\small \Leftrightarrow \space &\small t^2+t-a-1=0\\
\end{split}
上記は$\small t$に関する2次方程式となるため、$\small t$が$\small -1≦t≦1$の範囲で実数解を持つ条件を考えればよい。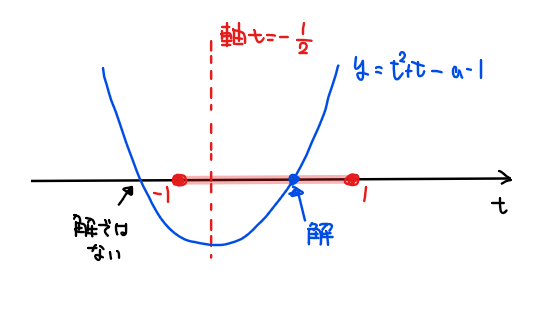

解の配置問題では、『軸の範囲』、『判別式』、『範囲の境界での$\small y$座標』の条件を確認すればよかったので、順番に確認していこう。
まず、軸についてだが、2次関数 $\small y=t^2+t-a-1$のグラフは、軸は$\small t=1/2$で固定のため、今回は条件の考慮は不要。
次に、判別式については、実数解を持つ必要があるので、
\begin{split}
\small D = &\small 1^2-4\cdot1 \cdot (-a-1)≧0\\
\small \Leftrightarrow \space &\small 4a+5≧0\\
\small \Leftrightarrow \space &\small a≧-\frac{5}{4} \space \cdots ①\\
\end{split}
最後に、境界条件については本問では$\small -1≦t≦1$の範囲で解を持つ必要があることから、$\small t=\pm1$が境界値となる。今考えている2次関数 $\small y=t^2+t-a-1$のグラフは、軸が固定されていて切片だけに文字 $\small a$を含んでいることから、$\small a$の値によるグラフの変動は、$\small y$軸方向の上下移動のみとなる。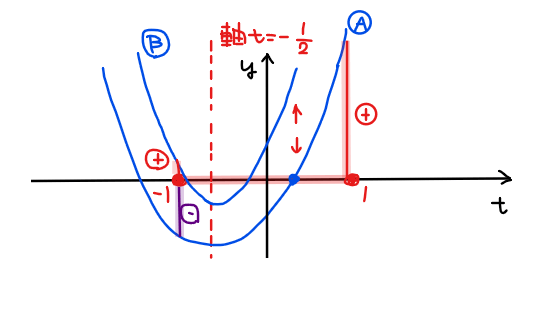

このことから、$\small t=-1$での$\small y$座標は、上図のように＋にも－にもなり得る（＝条件なし）が、$\small t=1$での$\small y$座標 $\small 1-a$は0以上になる必要があるので、
\begin{split}
&\small 1-a≧0\\
\small \Leftrightarrow \space &\small a≦1 \space \cdots ②\\
\end{split}
以上の①～②の共通範囲を求めることで、$\small \displaystyle -\frac{5}{4}≦ a ≦1$…【答】.

●補足
解の配置問題は一般的な解法のため使い勝手はよいが、研究の別解でも紹介の通り場合分けと条件の精査が大変になる傾向があるため、定数分離できる問題は定数分離して解く方がやはり簡単だろう。

【問題2】三角方程式の解の存在条件（難易度：★★★）

$\small \theta$の方程式 $\small 2\cos^2\theta+2k\sin\theta+k-5=0$を満たす $\small \theta$があるような定数 $\small k$の値の範囲を求めよ。

問題解決のKey

・問題1のようにきれいに定数分離ができない（無理やり分離も可能だが、左辺の三角関数が複雑な関数となってしまう）ため、$\small \sin\theta , \space \cos\theta $のみの三角方程式（2次式）に統一することで、2次方程式の解の配置問題に帰着させる。解の配置問題の解き方・考え方の詳細は、【解の配置問題】2次方程式の解の存在範囲（パターン別解法を徹底解説）を参照。

　解説

$\small \sin\theta =t$とおく。$\small \theta$の範囲指定がないため、一般に$\small -1≦\sin\theta≦1$となることから、$\small t$の取り得る値の範囲は$\small -1≦t≦1$。

問題の三角方程式を$\small t$を用いて表すと

\begin{split}
&\small 2\cos^2\theta+2k\sin\theta+k-5=0\\
\small \Leftrightarrow \space &\small 2(1-t^2)+2kt+k-5=0\\
\small \Leftrightarrow \space &\small 2t^2-2kt-k+3=0 \quad \cdots (*)\\
\end{split}

よって、方程式 $\small (*)$が$\small -1≦t≦1$の範囲に解を持つ条件を考えればよい。

解の存在条件を考えるにあたっては、下図のように、

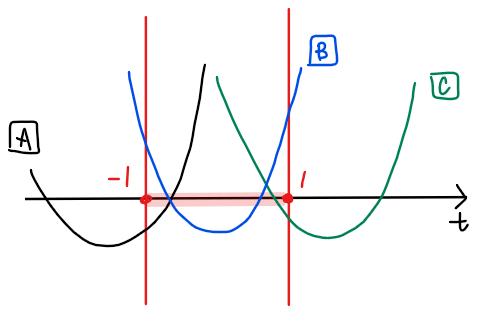
・パターンA：軸が$\small -1≦t≦1$より左側にある場合
・パターンB：軸が$\small -1≦t≦1$の内側にある場合
・パターンC：軸が$\small -1≦t≦1$より右側にある場合
の3パターンを考えればよい[*1]。

*1：【補足】軸の位置を3パターンで場合分けする理由
2次関数と$\small t$軸上の$\small -1≦t≦1$の部分との共有点の個数が解の個数になるため、2次関数と$\small -1≦t≦1$の部分が交わる（あるいは接する）場所が非常に重要になる。交わる（接する）場所を考える際に軸の位置を気にする理由としては、軸が$\small -1≦t≦1$の外側（右側 or 左側）にある場合は$\small -1≦t≦1$の範囲で2次関数は右肩上がりor右肩下がりのいずれかになり、軸が$\small -1≦t≦1$の内側にあるときは頂点を境に増加部分と減少部分がある概形になる、というように、この3パターンごとに$\small -1≦t≦1$内での2次関数のグラフの形（増加or減少）が変わるためである。
逆に言うと、この3パターンで場合分けしておけば、だいたいの問題は解くことができるので、「軸の位置で場合分けする」と覚えておくとよいだろう。

パターンA：軸が$\small -1≦t≦1$より左側にある場合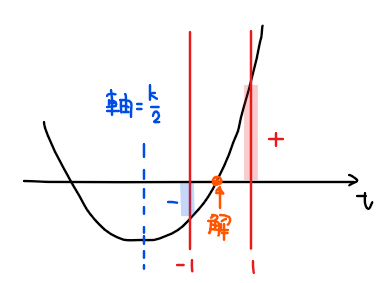

方程式 $\small (*)$の左辺の2次関数の軸は、$\small \displaystyle t=\frac{k}{2}$となるため軸が満たすべき条件は『軸 $\small <-1$』、すなわち
\begin{split}
&\small \frac{k}{2}<-1\\
\small \Leftrightarrow \space &\small \color{#ef5350}{k<-2 \space \cdots ①}\\
\end{split}
判別式が満たすべき条件としては、実数解を持っていればよいので、
\begin{split}
\small D/4 = &\small k^2-2\cdot (-k+3)≧0\\
\small \Leftrightarrow \space &\small k^2+2k-6≧0\\
\small ∴ \space &\small \color{#ef5350}{k≦-1-\sqrt{7},\space -1+\sqrt{7}≦k \space \cdots ②}\\
\end{split}
最後に、$\small -1≦t≦1$の範囲に解を持つための境界条件を確認する。範囲の境界は$\small t = \pm1$となるので、$\small t=-1$および$\small t=1$での$\small y$座標が満たすべき符号の条件を考えればよい。すると、今回のパターンでは、$\small f(t)=2t^2-2kt-k+3$とおくと、『$\small f(-1)≦0$かつ$\small f(1)≧0$』を満たせばよいので、
\begin{split}
\small f(-1)= &\small k+5≦0\\
\small \Leftrightarrow \space &\small k≦-5\\
\small f(1)= &\small -3k+5≧0\\
\small \Leftrightarrow \space &\small \displaystyle k≦\frac{5}{3}\\
\small ∴ \space &\small \displaystyle \color{#ef5350}{k≦-5 \space \cdots ③}\\
\end{split}
よって、①～③の共通範囲を求めると、$\small k≦-5 \space \cdots (A)$.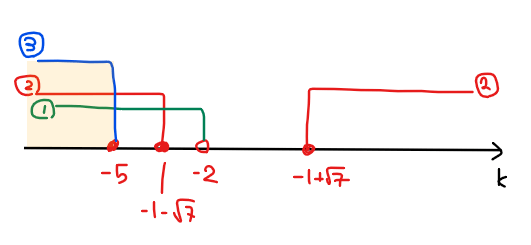

●補足
ちなみに、$\small -1-\sqrt{7}$と-2の大小関係は、両辺に1を足した$\small -\sqrt{7}$と-1を比較すればよく、負の数だと分かりにくいので、一旦、1と$\small \sqrt{7}$の大小比較を考えると、正の実数であれば両辺を2乗しても大小関係は変わらないので1と7の比較となり、$\small 1<7$ ⇔ $\small 1<\sqrt{7}$ ⇔ $\small -\sqrt{7}<-1$（－になると大小関係が逆転） ⇔ $\small -1-\sqrt{7}<-2$というように判断できる。

パターンB：軸が$\small -1≦t≦1$の内側にある場合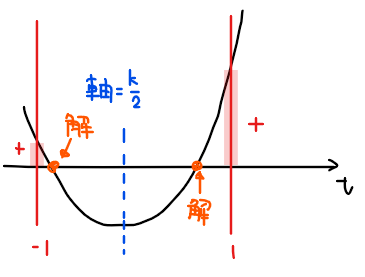

軸が満たすべき条件は『$\small -1≦$ 軸 $\small ≦1$』、すなわち
\begin{split}
&\small -1≦\frac{k}{2}≦1\\
\small \Leftrightarrow \space &\small \color{#ef5350}{-2≦k≦2 \space \cdots ④}\\
\end{split}
判別式が満たすべき条件はパターンAと同じ（②の条件）。
$\small -1≦t≦1$の範囲に解を持つための境界条件は、下図のように正になる場合も負になる場合もあることから、特定の条件はなし。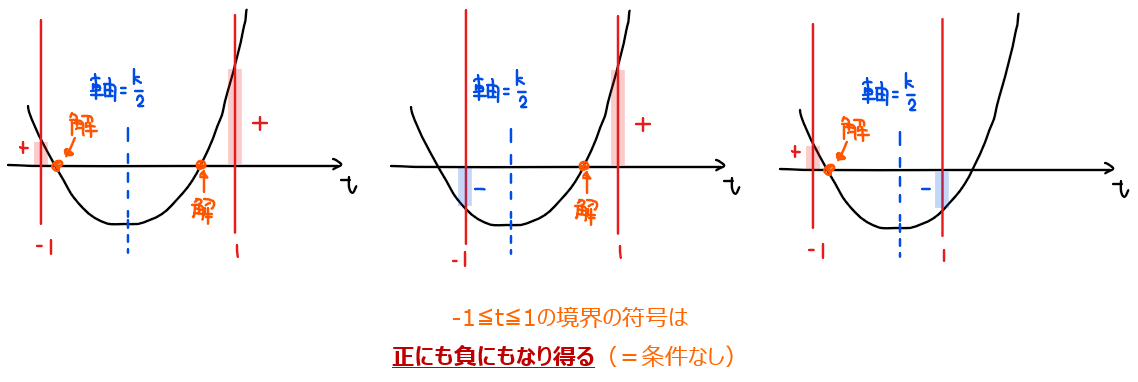

よって、②、④の共通範囲を求めると、$\small -1+\sqrt{7}≦k≦2 \space \cdots (B)$.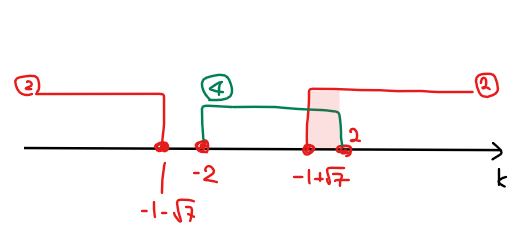

パターンC：軸が$\small -1≦t≦1$より右側にある場合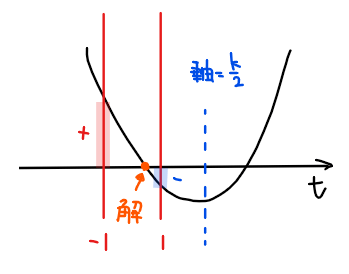

軸が満たすべき条件は、『$\small 1<$ 軸』、すなわち
\begin{split}
&\small1<\frac{k}{2}\\
\small \Leftrightarrow \space &\small \color{#ef5350}{2<k \space \cdots ⑥}\\
\end{split}
判別式が満たすべき条件はパターンAと同じ（②の条件）。
$\small -1≦t≦1$の範囲に解を持つための境界条件は、『$\small f(-1)≧0$かつ$\small f(1)≦0$』なので、
\begin{split}
\small f(-1)= &\small k+5≧0\\
\small \Leftrightarrow \space &\small k≧-5\\
\small f(1)= &\small -3k+5≦0\\
\small \Leftrightarrow \space &\small \displaystyle k≧\frac{5}{3}\\
\small ∴ \space &\small \displaystyle \color{#ef5350}{k≧\frac{5}{3} \space \cdots ⑦}\\
\end{split}
よって、②、⑥、⑥の共通範囲を求めると、$\small \displaystyle 2<k \space \cdots (C)$.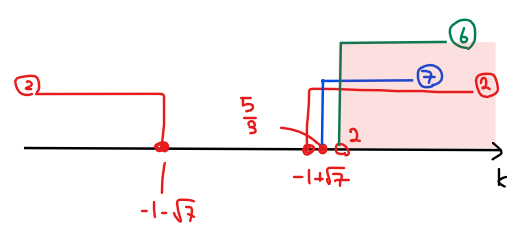

以上の（A）、（B）、（C）の3パターンが、方程式$\small (*)$が解を持つための$\small k$の値の範囲となることから、3パターンを合計した範囲が答えとなる。

よって、$\small k≦-5,\space -1+\sqrt{7}≦k$…【答】.

【問題3】不等式が常に成立する条件への応用（難易度：★★☆）

$\small \theta$がどのような角であっても、$\small P=\cos^2\theta -2a\sin\theta +a^2-4$が常に $\small P≦0$となるような $\small a$ の値の範囲を求めよ。

問題解決のKey

「常に不等式が成り立つための条件」と聞いて2次関数の「判別式<0」を利用して条件の絞り込みをする問題だと考えた人もいるかもしれない。しかし、三角方程式・不等式の2次式においては、ただの2次関数ではなく「-1以上1以下の範囲に制限された2次関数」であることに注意する必要がある。

　解説

$\small \sin\theta =t$とおくと、すべての$\small \theta$に対して$\small -1≦\sin\theta ≦1$ より、$\small t$は $\small -1≦t≦1$の値をとる。

また、

\begin{split}
\small P = &\small (1-t^2)-2at+a^2-4≦0\\
\small \Leftrightarrow \space &\small t^2+2at-a^2+3≧0\\
\end{split}

よって、問題の条件を満たす$\small a$の値は、不等式 $\small t^2+2at-a^2+3≧0$が$\small -1≦t≦1$の範囲で成り立つような$\small a$の値の範囲を求める問題と言い換えることができる。それはすなわち、『$\small -1≦t≦1$の範囲内で、不等式左辺の2次関数の最小値が0以上となる』ということと同値である[*1]。

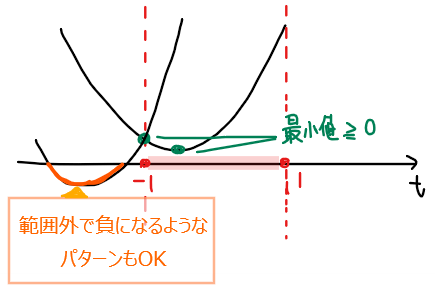
*1：【補足】
$\small -1≦t≦1$の範囲内で0以上であればよいということは、裏を返せば、$\small -1≦t≦1$の範囲外であれば負になってもOKということ。なので、必ずしも判別式 $\small D<0$（解を持たない条件）とはならないことに注意しよう。

左辺を$\small f(t) = t^2+2at-a^2+3$とおくと、

\begin{split}
\small f(t) = &\small (t+a)^2-2a^2+3\\
\end{split}

より、$\small f(t)$は軸が$\small t = -a$の2次関数なので、軸の位置について、

・パターンA：軸が$\small -1≦t≦1$より左側にある場合
・パターンB：軸が$\small -1≦t≦1$の内側にある場合
・パターンC：軸が$\small -1≦t≦1$より右側にある場合

の3つのパターンので場合分けをして、各々での最小値が0以上になる条件を確認すればよい。

パターンA：軸が$\small -1≦t≦1$より左側にある場合
軸$\small <-1$の場合なので、軸の条件は$\small -a<-1$ ⇔ $\small a>1$…①。
パターンAでは2次関数 $\small f(t)$は$\small t=-1$で最小値となるため、$\small f(-1)≧0$が満たすべき条件となるので、
\begin{split}
\small f(-1) =&\small -a^2-2a+4≧0\\
\small \Leftrightarrow \space &\small a^2+2a-4≦0\\
\small ∴ \space &\small \space \color{#ef5350}{-1-\sqrt{5}≦a≦-1+\sqrt{5} \space \cdots ②}\\
\end{split}
よって、①、②の共通範囲を求めると、$\small 1<a≦-1+\sqrt{5} \space \cdots (A)$.

パターンB：軸が$\small -1≦t≦1$の内側にある場合
$\small -1≦$軸$\small ≦1$の場合なので、軸の条件は$\small -1≦-a≦1$ ⇔ $\small -1≦a≦1$…③。
$\small f(t)$の最小値は頂点になるので、
\begin{split}
\small &\small -2a^2+3≧0\\
\small \Leftrightarrow \space &\small 2a^2≦3\\
\small ∴ \space &\small \space \color{#ef5350}{-\frac{\sqrt{6}}{2}≦a≦\frac{\sqrt{6}}{2}\space \cdots ④}\\
\end{split}
よって、③、④の共通範囲は、$\small -1≦a≦1 \space \cdots (B)$.

パターンC：軸が$\small -1≦t≦1$より右側にある場合
$\small 1<$軸の場合なので、軸の条件は$\small 1<-a$ ⇔ $\small a<-1$…⑤。
パターンCでは2次関数 $\small f(t)$は$\small t=1$で最小値となるため、$\small f(1)≧0$が満たすべき条件となるので、
\begin{split}
\small f(1) =&\small -a^2+2a+4≧0\\
\small \Leftrightarrow \space &\small a^2-2a-4≦0\\
\small ∴ \space &\small \space \color{#ef5350}{1-\sqrt{5}≦a≦1+\sqrt{5} \space \cdots ⑥}\\
\end{split}
よって、⑤、⑥の共通範囲を求めると、$\small 1-\sqrt{5}≦a<-1 \space \cdots (C)$.

最後に、（A）、（B）、（C）の3パターンで求めた範囲を合計したものが答えとなることから、$\small 1-\sqrt{5}≦a≦-1+\sqrt{5}$…【答】.

本記事のまとめ

今回は三角方程式の解の個数と解の存在条件について徹底解説していきました。

解き方としては

・『三角関数を含む関数』＝『定数』の形に定数分離して解く。
・定数分離ができない場合は、2次方程式の解の配置問題として解く。

の2パターンで考えるのが王道です。また、三角方程式の解の配置問題は、以下の三角関数の特徴を踏まえながら解くことがポイントです。

Point：三角方程式の解の配置問題

・2次の三角方程式は、$\small -1$以上$\small 1$以下の範囲（※）に制限された2次関数とみなせる。
　※角度$\small \theta$の範囲によって変動する可能性あり
・解の個数は、$\small -1 \space or \space 1$のときに1個、$\small -1$より大きく$\small 1$未満のときに2個となる。
・解の存在条件は、2次関数の軸が$\small -1$以上$\small 1$以下の範囲の左側、範囲内、右側の3パターンに場合分けするのが定石。

それでは今回は以上です。お疲れさまでした！